空間図形の表面積 （円すいも超理解する）

［関連ページ］おうぎ形は円の一部と考える

［前のページ］空間図形（体積）

前回やったように、
コンビニにあるジュースで説明すると

体積と表面積はこういうことでした。
（紙パックだと厳密には「のりしろ」があるけどね）

前回は体積、今回は表面積！！

ーーーーーー

【表面積の解き方と展開図の描き方】

表面積の「面積」ってそもそも、

こうやって「平面」の大きさを表すものだったよね。

だから立体の表面積は、開いて平面にして考えます。
とりあえず問題！

表面積を求めるには、まず、開く。
この開いた図を展開図（てんかいず）って言うんだけど、
意外とうまく描けない人が多いんだよね。

楽な方法教えます！
まず横（側面）から描いちゃうんです。

上の立体は底面が四角形、
だからサイドは４辺分あるということです。

これだけ。
四角形だから４つ描けばいいだけです。

そのあと、底面を上と下につけちゃう。

これでほぼ完成です。

そしたら、長さの情報を書き込みます。

長さは、必要な分はすべて書きます。
（書き込みすぎないバランスも大事です）

まず側面積（側面の面積）から。

これ、４枚あるけど、
大きな１枚として考えることもできます。

横の長さが（３＋２＋３＋２）ｃｍ、
縦の長さが１０ｃｍです。

これでおわり！

次は底面積ね。

上も下も両方合わせて底面積です。
上も下も同じだから、ひとつ出して、２倍します。

これを合わせたのが表面積です。

これだけ！これで答えです。

ちなみに、

こういうふうに一気に解いてもいいです。
一気に解くときは計算ミスしないように気をつけてね。

とにかくこれが表面積の基本です。
展開図を描くのが一番大事。めんどくさがらないようにね。

ーーーーーー

前回やったけど、体積には２種類あります。
まず「〇〇柱（ちゅう）」

そして「〇〇錐（すい）」

結局「とがってないの」と「とがってるの」です。

まず「〇〇柱」からやるね。
さっき四角柱やったから、三角柱やってみようか。

まず展開図！
大きめに描いてください。

三角形だから、側面は３つです。

こうして

底面積つけたして。

そして長さを書き込みます。

長さをきちんと書き込めるように、
大きく描いとくんだからね！

５ｃｍ、７ｃｍ、３ｃｍは、厳密に描かなくて（も）いいです。
あくまでメモ。簡単にわかりやすく。

そして三角形の情報は「底辺と高さ」だけでいいよね。
必要なのだけ。

じゃあ解くね！

展開図さえ描けばそんなに難しくない。

はい、じゃあ円柱（えんちゅう）！

展開図を描きます。
予想できる？

円柱は、「円」で角がないから、側面はひとつです。

ここで足りない情報があるんだけど、分かるかな。
よく見て、よく考えて。

側面の「横の長さ」がないじゃん。
これじゃあ側面積（長方形）求められない。
どうしよう？

側面積の横の長さは。

ここと一緒です。円の周りの長さ。
つまり円周（えんしゅう）だね。

ここで、円とおうぎ形のページでやった、
円の面積と円周の公式を復習しときます。

半径をｒ、円周率をπ（パイ）だとして、
円周は「２πｒ」、円の面積は「πｒ²」だったね。

これはもう覚えてるかな？
覚えてない人は連呼（れんこ：何度も声に出して読む）すること。
覚えるんだよ。今！

（πｒ²、πｒ²、πｒ²、パイアール２じょう、パイアール２じょう、パイアール２じょう、パイアール２じょう・・・）

（２πｒ、２πｒ、２πｒ、にーパイアール、にーパイアール、にーパイアール、にーパイアール、にーパイアール・・・）

はい覚え（たとし）ました。
じゃあ、気をつけながら解いていくよ！

「２πｒ」と「πｒ²」は毎回書いておくことで、
忘れにくいし、見ながら解けて楽です。

これで「〇〇柱」はおしまい！

ーーーーーー

【〇〇錐の表面積】

じゃあ「〇〇錐（すい）」にいきます。

とりあえず展開図だったね。
この場合は底面積から描きます。四角いっこ。

そしたら周りに４つ三角。

そしたら長さを書き込むんでした。

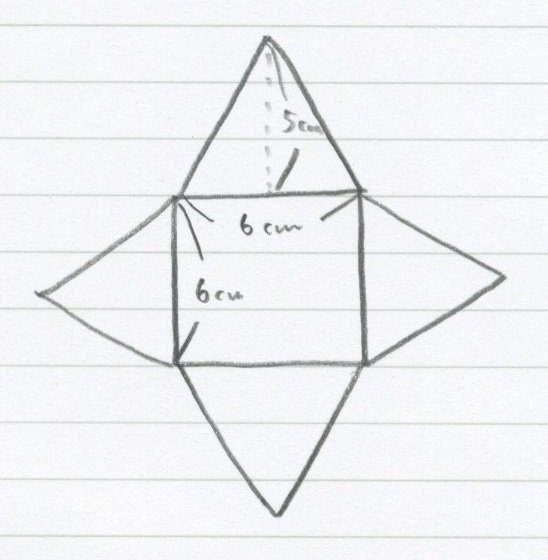
これだけ！
答えるよー！

こんな感じでした！
別に問題なかったね。

ーーーーーー

【円錐の解き方】

最後に円錐（えんすい）をやります。
ダントツでむずいし、みんなきらいな円錐！

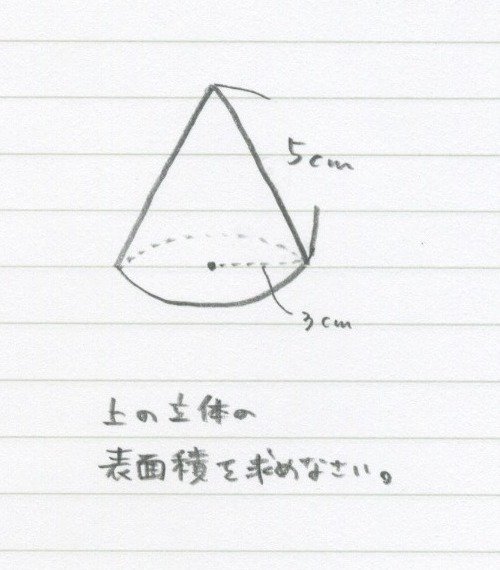
まず展開図を描きます。
底面は円。

これに対して、側面はおうぎ形です。

これに長さを書き込みます。

・・・・・。
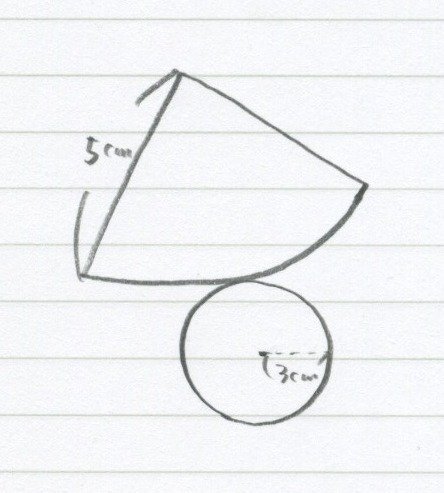
で・・・・・？
何すればいいんだ・・・。

と、ここでなることが多い円錐問題。
（展開図を描いてるだけえらい）

底面積は大丈夫そうだよね。「πｒ²」だし。
問題は側面積、あのおうぎ形です。

ということで、少し前におうぎ形を教えていたんでした。
そっちを先に読んでくるのがいいと思います。

なぜなら、ここはそこよりレベルが高いから。
おうぎ形の知識があることを前提で教えていくからね！

そのページで、
おうぎ形は「円の一部と考える」と説明しました。
図のおうぎ形に、点線で円を描き込んでください。

おお！
少しイメージがくっきりしました。
大きい円の半径が５ｃｍ、って感じがしてきたね。

おうぎ形の求め方は

　おうぎ形は「円の一部」と考える

　→「おうぎ形（部分）」＝「円（全体）」×「割合」

でした。
おうぎ形は「部分」と「全体」を意識することが大事だったね。

じゃあおうぎ形の面積。
これを部分とすると、全体は？

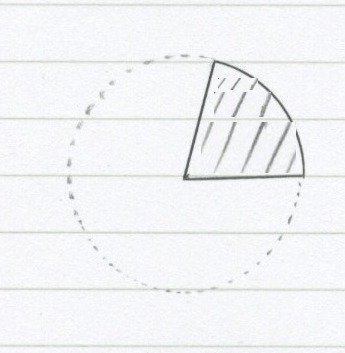
「円の面積」だ。

だから

「おうぎ形」＝「円（全体）」×「割合」

これは、面積の場合は

「おうぎ形の面積」＝「円の面積」×「割合」

にすればいいってことです。

つまり、さっきの問題のおうぎ形の面積を求めるには
円の面積が必要だ。
円の面積は「πｒ²」でよさそうだね。

じゃあ「割合」はどうしよっか！
どうしよっか・・・・。
え・・・・・？

さあここで、割合ってなんだっけ。
（割合もおうぎ形のページでやってるからね！）

割合は

こう！割合は「全体分の部分」。

おうぎ形は「円の一部」と考えるんだから、
おうぎ形が「部分」、円が「全体」だね。

これを踏まえると、おうぎ形のページでやったように、
おうぎ形の割合は３パターンも作れました。

ここでもっかい問題見てみよっか！

全部ないじゃん。

全部ないじゃん。（２度目）
でもこの３パターンしかない。

決定的にだめなのはどれかを考え直します。

　角度・・明らかに分かっていない
　円周・・円周は分かるけど弧の長さがわかんない
　面積・・これから面積求めるんだから使えない

角度と面積から攻めても絶対ダメそう。
だから狙うは「円周」です。

円周は「２πｒ」だったね。
でも「弧の長さ」はなーー。

よーく見て。弧の長さ。
さっき、似たような考え方を使ってるんだから。

よーく見た？
わかった？

よく見て。
きっとわかるから、よく考えて。
もう、答え言うからね。

この考え方です。

この長さと同じじゃんね。
「大きい円の弧の長さ」は、
「小さい円の円周」と長さが一緒なんです。

ん？
伝わった？

さっきの３つのうちの１つ。
これを使って「割合」を出すには、
「円周」と「孤の長さ」を出す必要があります。

この「弧の長さ」として
「小さい円の円周」を使っていいってことです。

大きい方の円に注目してね。
おうぎ形を求めるために

これが必要ってことは、
円の円周とは「大きい円の円周」のことです。
で、「孤の長さ」は「小さい円の円周」。

じゃあ今回の割合は、
こうやって円周を使って求められるねってことです。

むずかしいと思うけど、とりあえず解くよ！
だから、側面積は「πｒ²」×「割合」で

こうです。
ちゃんと分数が上下どっちも「２ × π × ｒ」になってるね。
解説は長かったけど、式自体はシンプル。

じゃあ底面積も合わせて、表面積求めるよ。

これで答えです。

ーーーーーー

【覚えなくていい公式】

ちなみに。
円錐の側面積の求め方はね。

こういう一発で解く方法があります。
覚える？
覚えても別にいいです。

でも、いらないよこんなの。
さっき解けたもんね。
難しかったけど、
あと３回は解けばもっと理解できます。

同じ解き方をずっと続けてれば、
理解はどんどん深くなって、
どんどん間違えなくなります。

だけど

「円錐のやり方はこれで一発！」
「この解き方はこれで解ける！」
「この問題はこれで一撃！」

これを全部覚えたら、
理解はどんどん浅くなる。
丸暗記だから忘れたらアウトだし、
丸暗記だから応用にめっちゃ弱いです。

こういう、
理解をともなわない「テクニック」っていうのは、危ないんだ。
それもよく覚えててほしいなと思います。

ちなみに。
なんでその公式になるのかというとね。
半径をａ、ｂにして、さっきと同じ解き方をしてみます。

こうなるから。
理解でできるものは、覚えないほうが実はお得です。

ーーーーーー

ということで表面積の回はここでおしまい！
そして、このサイトの数学全体としてもここでおしまいです。

全部やった人がいたら、すごい。
きっと前より、出来るようになってると思います。
好きになってたらそりゃあいいけど、
好きまではいかなくても、
「嫌い」とか「苦手」とかじゃなくなってるといいな。
感想あったら教えてね。

最後の練習問題は［前のページ］の体積も合わせて。
空間図形の総復習です。

［練習問題］答えは下

［全ページに飛べるもくじ］

［答え］