
2022年度MLBシーズンでポストシーズン出場する為には…part 1 .5(関係性を表すヒートマップとは…?)
2022年度MLBシーズンでポストシーズン進出に出場する為には…part 1 .5(関係性を表すヒートマップとは…?)
前回の記事で説明をしたデータを基に分析、そして予測等を進めていく過程で、データ間の関係性を理解することは非常に大切なことになります。
データ間の関係性とは…?

例えば、1000円のお小遣いで600円の物を買った際に手元に残るお金400円です。この場合1000円というデータから600円というデータでを引いた為400円という新たなデータが発生したことになります。これらの数値が一つでも変わると最後に算出される数値が変わってきます。つまり片方の数値が変わると、もう片方の数値も変わるデータを関係性のあるデータと言います。一方で、片方の数値が変わってももう片方の数値は変わらない場合は関係性のないデータと判断する事が出来ます。
データ間の関係性を理解することで特定のデータに焦点を当てた場合、どのデータが必要でどのデータが不要なのか求める事が可能だからです。そしてそのデータ間の関係性を可視化する際に重要な役割を果たす…それヒートマップです。
ヒートマップとは何か…?
Heatmap(ヒートマップ)とはデータを色分けすることによってデータを可視化してくれるグラフです。馴染み深い物だと、天気予報時の雨雲レーダーなど、色を変えてその数値の変化をわかりやすく可視化している物です。
今回の分析で使われるヒートマップは、データ毎の関係性の度合いに応じて色が変化しています。
データ間の関係性はどの様にして求められるのか…?
データ間の求め方は…

簡単にいうと、データ xとyの共分散 ÷ (xの標準偏差)✖️(yの標準偏差)となっています。ですが幸運にも今回はjupyter notebookというプログラミングプラットフォームにて分析を行う為、相関性計数を求める関数がテンプレートとしてある為この様な複雑な計算をする必要はありませんでした。
正の相関と負の相関とは…?
導き出された相関係数には大きく分けて2つの傾向があります。それは数値が1に近いものと、-1に近いものです。相関係数の数値の幅は最大1の最小-1となっています。そして1に近い数値は正の相関と呼ばれ、-1に近い数値は負の相関と呼ばれます。
正の相関
正の相関とは、片方のデータの数値が増えるともう片方のデータの数値も増える傾向がある関係性を指します。数値では0以上1以下の数値となります。 ex,(0.95, 0.13, 0.67…)
例えば、身長が伸びると体重が増える傾向がある…ect
負の相関
負の相関とは、片方のデータの数値が増えるともう片方のデータの数値は正の相関とは逆に下がる傾向がある関係性を指します。数値では、-1以上0以下の数値となります ex,(-0.95, -0.24, -0.01…)
例えば、外の気温が上がると、家のクーラーの温度が下がる傾向がある…ect
ヒートマップはどの様にして見るべきなのか…?
今回のヒートマップでは暖色は正の相関、寒色は負の相関と振り分けられています。今回のちに使用されるヒートマップを例として載せておきます。
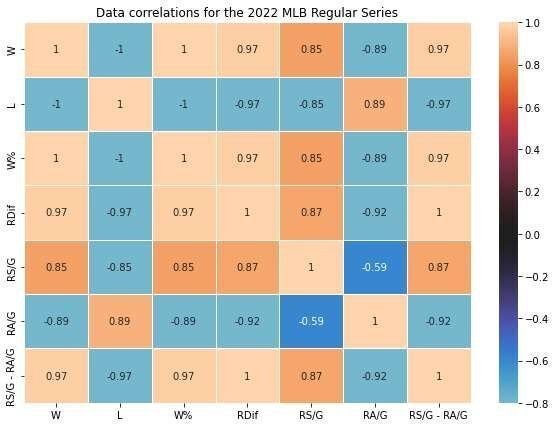
このヒートマップを見ると、データW(勝利数)に対して正の相関なのはW%(勝率)、RDif(得失点差)、RS/G(1試合平均得点)、RS/G - RA/G(1試合平均得失点差)である事が分かります。一方でL(敗数)とRA/G(1試合平均失点)は負の相関であると言えます。
ヒートマップからどんな事が分かるのか…?
あるデータ(X)の数値をどの様にして上げる必要があるのかを求める際には、そのデータと正の相関をもつデータ(Y)に焦点を当ててそのデータ(Y)のデータ向上をする為の方法を模索すると、データ(X)の数値向上につながります。
一方で、データ(X)の数値を下げたい時は、負の相関をもつデータ(Z)の数値をどの様に上げるのか模索する事で、今後の分析や予測に役立ちます。
今回の記事はここまでとなっております。この記事の前に投稿しているpart 1にてデータ分析に使用するデータの説明を行っている為、そちらを参照ください。
次回の記事ではいよいよ分析パートに入って行きます。
