野球の試合で勝利するために必要なものとは

野球の目的を「勝利」と定義したとき、勝利のために必要なものとはいったい何でしょうか。
数字では測れないような貢献もありますが、ここでは誰が見ても同じ尺度で測れる客観的な数字を使ってそれを探っていきたいと思います。
過去のリーグ戦の各チームの成績を見ると勝率の高いチーム、低いチームにはそれぞれ共通する特徴があります。それは勝率の高いチームは得失点差のプラスが大きく、低いチームは得失点差のマイナスが大きいということです。

上記の図は2リーグ制が導入された1950年以降の各チームの得失点と勝率の関係を表した図です。縦の軸が得失点、横の軸が勝率を表しています。図を見れば得失点（縦軸）の値が高いと勝率（横軸）の値が高くなるという傾向がわかると思います。

この傾向を踏まえてチームの得点と失点から勝率を予測するという予測式があります。セイバーメトリクスの第一人者、ビル・ジェームズが考案したピタゴラス勝率です。

ピタゴラス勝率
得点^n/(得点^n+失点^n)

nの値はリーグによってそれぞれ当てはまりの良い数字があり、NPBの場合は1.72乗にすると当てはまりがよくなると言われています。
実際に上記の予測式で2017年にセ・リーグで優勝した広島東洋カープの勝率を得点と失点から予測してみます。

2017　広島　得点736　失点540
736^1.72 / (736^1.72+540^1.72)
= 85315.87331 / (85315.87331+50086.10584)
= 85315.87331 / 135401.9791
=0.630（小数第四位を切り捨て）

実際に2017年の広島東洋カープが記録した勝率は0.633であり上記の予測式が実際の勝率と近いことがわかります。もちろんこの式は予測式であって実際には予測から外れた値が出ることもありますがだいたいの見当をつけることが可能です。次にピタゴラス勝率と実際の勝率の関係を表した図を記します。

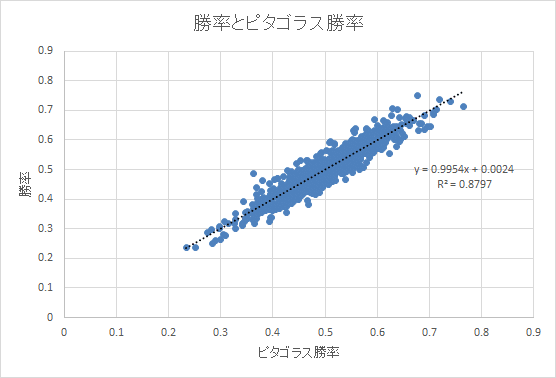
横軸がピタゴラス勝率、縦軸が勝率を表しています。
図中の黒い点線は説明変数がピタゴラス勝率、目的変数が勝率の予測式から引かれた直線です。（これを回帰直線と呼びます。）
図を見ると点線に沿って各値がプロットされていることがわかります。予測式の当てはまりの良さを示す決定係数（図中のR^2）は0.8797であり非常に良く当てはまっているという結果が得られました。（決定係数は一般的に0.80を超えると非常に当てはまりが良いとされています。）これはピタゴラス勝率は実際の勝率に8割から9割は当てはまるということを意味します。
ピタゴラス勝率の計算式を見てみると得点の数が多いほど、失点の数が少ないほど予測される勝率が高くなります。このことからチームの勝率を上げるには得点を増やすこと、失点を減らすことが重要と言うことがいえます。得失点は勝利を得るための通貨と考えられます。