平均的なフォーシームは失点しやすいのかをスイング_Runから考察する

「打者は平均的な軌道を想定しているので平均的な変化量のフォーシームは打たれやすい」よく聞かれる言説だがこれは本当だろうか。また「ホップするフォーシームは空振りを奪えるがフライを打たれやすいという欠点がある」「沈むフォーシームはコンタクトされやすい欠点があるがゴロを打たせられるというメリットもある」とホップするフォーシーム、沈むフォーシーム、どちらにもメリットとデメリットがあるとも言われる。これらの言説を実際に検証してみることにする。

Run Value(RV)

試合の目的は勝利である。そして投手が勝利のためにできることは失点を抑止することだ。それならば評価の単位は失点にすることが妥当だろう。セイバーメトリクスでは得点期待値を用いあらゆるプレーを得点価値に換算することができこの得点価値を用いればフォーシームの縦変化量が失点抑止に与える影響を定量化することが可能となる。

Run Valueで球質を評価する

球質のみを純粋に評価するために今回は評価の対象イベントを打者のスイング時に限定する。これは見逃しストライク・ボールは投手の制球力に依存するところが強く球質を評価するうえで適当ではないと判断したからだ。そして打者のスイング時のイベントを実際に得点価値にしたものが以下の表だ。

（3/21　打球種類の定義について追記）

Run Valueは平均と比較してどれだけ得点を増やしたかと言う観点から算出した数字だ。投手にとってはプラスが大きいほど失点を生み出しマイナスが大きいほど失点を抑止したことを意味する。ただこれは全球種の平均値である。今回知りたいのはストレートの縦変化量別Run Valueだ。そこで空振りとファウルを除いた打球の得点価値は縦変化量別に算出した。

39.2～46.7cm等と書かれている数字はボールの縦変化量を意味する。2015-2020のMLBの縦変化量平均である42.9cmを基準に約ボール1個分(7.5cm)ずつ縦変化を区切り各変化量での打球タイプ別の得点価値の平均を取った。これらを基準にスイング100回あたりのイベント発生頻度×得点価値の総和を取り各縦変化量別のスイング_Run/100を算出する。

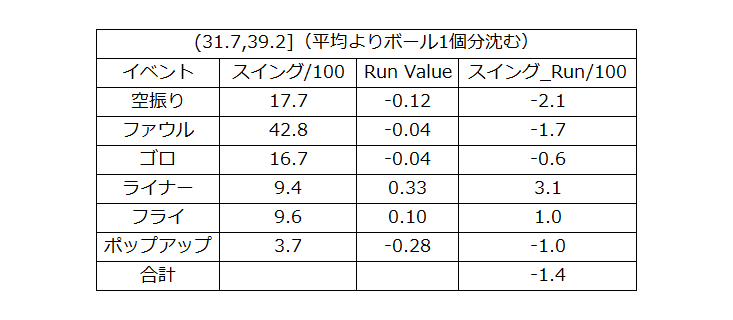
結果は以上のようにホップの量は多ければ多いほど失点を抑止しやすいということがわかった。平均より沈むフォーシームは平均的なフォーシームより失点しやすく冒頭の言説は正しくないことがわかる。イベントの発生頻度を見てみるとホップの量が多いほど空振りが多くライナーの発生頻度が低くポップアップの発生頻度が高くなる。この3つのイベントは比較的Run Valueの影響が大きいことから全体のスイング_Runに影響を与えたと思われる。

各項目のRun Value

（追記　3/21）

ここらかは各項目のRun Valueを見ていく。

・空振り_Run

基本的に縦変化量が多いほど空振りの発生割合は高くなる。上位と下位で0.8点程度の差がついた。

・ファウル_Run

ファウルは縦変化量が多いほど発生頻度が高くなる。ただし発生頻度に差がつきにくいためほとんどRunで差はついていない。

・ゴロ_Run

ゴロは縦変化が小さいほどRun Valueが低下しやすいことに加え発生頻度が高まることから上位と下位で0.7点程度の差がついている。ゴロで失点を抑止する効果は一定以上ありそうだ。

・ライナー_Run

ライナーはRun Valueの絶対値が比較的大きな値であることから発生頻度の差が小さくても全体のRunに与える影響が大きい。フェア打球の発生割合自体を低く抑えられていることに加えライナーの得点価値自体も低下しているホップ量の大きいフォーシームに分があるようで上位と下位で1.1点ほど差がついている。

・フライ_Run

フライのRun Valueは縦変化量が大きくなるほど低下することとフェア打球の少なさで相殺されたこともあってか発生頻度に差がついておらず全体で見ると縦変化量の大きいフォーシームの方がRunの上昇を抑えられている。ただし差にして0.2点程度と影響は大きくない。

・ポップアップ_Run

ポップアップの発生頻度は縦変化量が大きいほど上がっている。上位と下位で0.6点程度の差がついている。

・フェア_Run

フェア_Runは以上のようになった。縦変化量の大きいフォーシームはフェア打球の発生頻度が少なく打球による失点リスクそのものを抑えることに成功している。加えて変化量の高いストレートは打球の価値そのものを低下させている。

表は　100打球あたりの各打球の発生頻度×各打球のRun Value　で算出した各変化量の100打球当たりの失点リスクである。打球の失点リスクと言う面で見ると確かに縦変化の小さい速球はゴロで失点抑止を稼いでいるがフライはフライ打球そのものの価値の低下もあってあまり差がついておらずRun Valueの絶対値が高いポップアップの発生頻度の差によって縦変化量の大きいフォーシームに後れをとっている。結果としてみると打球の失点リスク単体で評価しても縦変化量の大きいストレートに分があるという結果になった。「縦変化量の小さいストレートはフライが減りゴロが増えるので打球の失点リスクが低くなる」という言説自体も見直す必要がありそうだ。

聞こえの良い言説に惑わされていないか

検証の結果、フォーシームのホップの量は多ければ多いほど失点を抑止することがわかった。この結論は「ノビ・キレのあるストレートが良いストレートだ」という旧来の価値観と一致しており別に特別新しいというものではない。だがそれならなぜ「ホップするフォーシームは空振りを奪えるがフライを打たれやすいという欠点がある」「沈むフォーシームはコンタクトされやすい欠点があるがゴロを打たせられるというメリットもある」という言説が広まってしまったのだろうか。これは推測だがデータを基に新しい言説が生まれたというのが一見聞こえが良いからではないだろうか。また旧来の評価では良くないとされた伸びない球質にも良いところはあるというのも「みんな違ってみんないい」というような一種の聞こえの良さがある。聞こえの良い言説が現れると惑わされがちだが大事なのは真実がどうであるかだ。そしてそのためには定量化を試みるなどといったアプローチが必要になってくる。
　トラッキングデータは未開拓な部分が多い分野だ。そのため色々な言説が生まれることがある。聞こえの良い言説に流されがちになってしまうのが人間と言うものだがそれに惑わされず真実を求める姿勢を大事にしたい。

今回の分析に使用したデータはBaseball Savantから入手した。
https://baseballsavant.mlb.com/

RE288の計算にはBill Pettiのbaseballrを使用した。
http://billpetti.github.io/baseballr/

スイング_Runのアイデアは「空振りを取るか、打たせて取るか　ストレートの性質を考察する」から得た。

https://1point02.jp/op/gnav/column/bs/column.aspx?cid=53379

#dfには2015-2020のstatcastのデータに加え
#あらかじめbaseballrで計算したRE288が入った列を作成済み
#（列名がre24になっているが中身はRE288)

#必要な列に絞る
df <- df %>%
 select(pitch_type,type,release_speed,pfx_x,pfx_z,description,
        launch_angle,launch_speed,events,re24)
        
#必要な列を作成  
df <- df %>%
 mutate(swingmiss_value = ifelse(description == "swinging_strike"|description == "swinging_strike_blocked"|description == "foul_tip" |description == "bunt_foul_tip",re24,NA),
        foul_value = ifelse(description == "foul" |description == "foul_bunt",re24,NA),
        GB_value = ifelse(launch_angle < 10 ,re24,NA),
        LD_value = ifelse(launch_angle >=10 & launch_angle < 25 ,re24,NA),
        FB_value = ifelse(launch_angle >=25 & launch_angle < 50 ,re24,NA),
        PU_value = ifelse(launch_angle >=50 ,re24,NA),
        pfx_z_cm = pfx_z *30.48,
        swing_denom = case_when( 
          description == "swinging_strike" ~ "1",
          description == "swinging_strike_blocked" ~ "1",
          description == "called_strike" ~ "0",
          description == "foul_tip" ~ "1",
          description == "bunt_foul_tip" ~ "0",
          description == "foul" ~ "1",
          description == "foul_bunt" ~ "0",
          description == "ball" ~ "0",
          description == "blocked_ball" ~ "0",
          description == "pitchout" ~ "0",
          description == "hit_by_pitch" ~ "0",
          description == "hit_into_play" ~ "1",
          description == "hit_into_play_score" ~ "1",
          description == "hit_into_play_no_out" ~ "1",
          description == "missed_bunt" ~ "0"),
          swing_denom = as.double(swing_denom),
        GB_FL = ifelse(type =="X" & launch_angle < 10 ,1,0),
        LD_FL = ifelse(type =="X" & launch_angle >=10 & launch_angle < 25 ,1,0),
        FB_FL = ifelse(type =="X" & launch_angle >=25 & launch_angle < 50 ,1,0),
        PU_FL = ifelse(type =="X" & launch_angle >=50 ,1,0),
        swingmiss_FL = ifelse(description == "swinging_strike"|description == "swinging_strike_blocked"|description == "foul_tip",1,0),
        foul_FL = ifelse(description == "foul",1,0))

        
#1球イベント得点価値を計算、swingmiss,foul
RV <- df %>%
 dplyr::summarise(Swingmiss = mean(swingmiss_value, na.rm = TRUE),
                  foul = mean(foul_value, na.rm = TRUE))
                  
#打球得点価値を計算
RV_BattedBall <- df %>%
　filter(type =="X")%>%
 dplyr::summarise(GB = mean(GB_value, na.rm = TRUE),
                  LD = mean(LD_value, na.rm = TRUE),
                  FB = mean(FB_value, na.rm = TRUE),
                  PU = mean(PU_value, na.rm = TRUE))

#縦変化量別打球価値を計算

Group <- seq(24.2,61.7,7.5)

df$pfx_z_cm_bin <- with(df, cut(pfx_z_cm, Group))

RV_pfx_z <- df %>%
 filter(type =="X" & pitch_type == "FF")%>%
 group_by(pfx_z_cm_bin) %>%
 dplyr::summarise(GB = mean(GB_value, na.rm = TRUE),
                  LD = mean(LD_value, na.rm = TRUE),
                  FB = mean(FB_value, na.rm = TRUE),
                  PU = mean(PU_value, na.rm = TRUE))
                  
write_csv(RV_pfx_z,"縦変化別打球価値.csv")

#縦変化量別イベント割合を算出

pfx_z_events_pct <- df %>%
 filter(swing_denom == 1& pitch_type == "FF")%>%
 group_by(pfx_z_cm_bin) %>%
 dplyr::summarise(N = n(),
                  Swingmiss_pct = sum(swingmiss_FL, na.rm = TRUE) / N *100,
                  foul_pct = sum(foul_FL, na.rm = TRUE) / N *100,
                  BattedBall = 100 - (Swingmiss_pct+foul_pct))
                  
write_csv(pfx_z_events_pct,"縦変化量別イベント割合.csv")


#launch_angleのNAになってる行を除外
df_jogai <- subset(df, !(is.na(df$launch_angle)))

#打球割合を算出、後でExcelでBatedBall * 各打球割合　を計算して100スイング当たり打球数を算出する
pfx_z_battedball_pct <- df_jogai %>%
 filter(swing_denom == 1 & description != "foul"& pitch_type == "FF")%>%
 group_by(pfx_z_cm_bin) %>%
 dplyr::summarise(N = n(),
                  GB_pct = sum(GB_FL, na.rm = TRUE) / N ,
                  LD_pct = sum(LD_FL, na.rm = TRUE) / N ,
                  FB_pct = sum(FB_FL, na.rm = TRUE) / N ,
                  PU_pct = sum(PU_FL, na.rm = TRUE) / N )
                  
write_csv(pfx_z_battedball_pct,"縦変化量別打球割合.csv")