情報で捉える生物学入門#11【生態学】
生態学では、種や同じ種の個体の集まりである個体群を基本単位として、それらの相互作用により何が起こるかを明らかにすることで、生態系で起こる現象を理解していく。今回は今まで扱ってきた分子・細胞・個体よりも空間・時間スケールの大きな個体群や種に着目することで、私たちの生活とも密接にかかわるマクロな生物学を扱う。
個体群の成長
生物の個体数は生態系を特徴づける重要なパラメーターの1つである。個体数は移入や移出によっても変化するが、ここでは簡単のため、個体の生死による個体群の成長をモデル化する。個体群の成長が制約を受けず、個体群密度の変化率が個体群密度自身に比例する場合、個体群密度は以下の微分方程式に従い変動する。
$$
\frac{dN}{dt} = rN
$$
Nが個体群密度であり、rは単位時間当たりの出生率から死亡率を引いた個体群の成長速度で、内的自然成長率と呼ばれる。
この微分方程式を解くと、個体群密度は以下の式・シミュレーションのように指数関数的成長を示す。
$$
N = N_0e^{rt}
$$
!pip install japanize-matplotlib
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
# 指数関数的成長のパラメータ
r_exp = 0.2 # 内的成長率(指数関数的成長)
N0_exp = 10 # 初期個体群サイズ(指数関数的成長)
T = 10 # タイムステップ数
# 時間配列
time = np.arange(T)
# 指数関数的成長のシミュレーション
N_exp = np.zeros(T)
N_exp[0] = N0_exp
for t in range(1, T):
N_exp[t] = max(0, N_exp[t-1] + r_exp * N_exp[t-1])
# 指数関数的成長のプロット
plt.figure(figsize=(10, 6))
plt.plot(time, N_exp, label="指数関数的成長 (r = 0.2)")
plt.title("指数関数的成長")
plt.xlabel("時間")
plt.ylabel("個体群サイズ")
plt.grid()
plt.legend()
plt.show()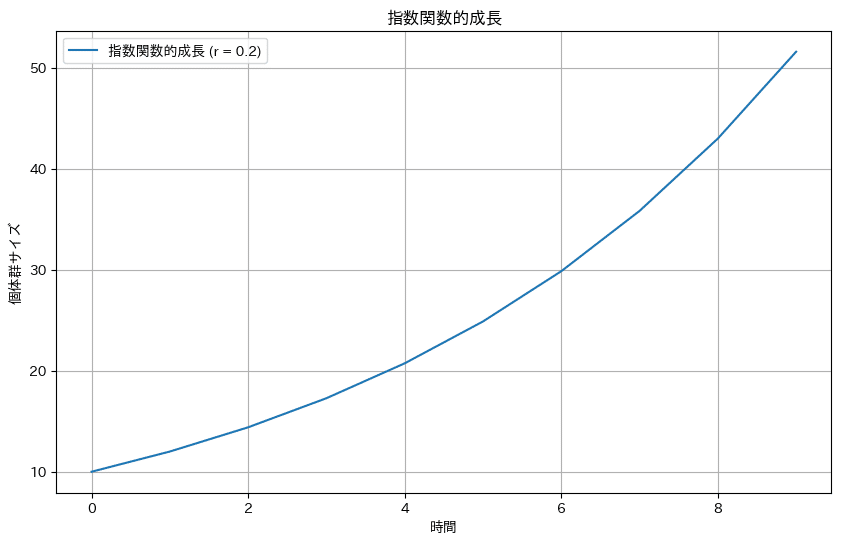
ロジスティック成長シミュレーション
実際の個体群は個体数が増えるにつれて食物や住処が不足するとともに病気の蔓延などにより、個体群密度が環境収容力Kに近づくにつれて増加率が低下する。この成長はロジスティック成長と呼ばれ、以下の微分方程式で記述される。
$$
\frac{dN}{dt} = rN(1-\frac{N}{K})
$$
ここで、Nが個体群密度、rが最大成長率である内的自然成長率、Kが環境が支えることが出来る個体群の最大密度である環境収容力である。このモデルでは、$${N\ll{K}}$$のときには$${\frac{N}{K}}$$が無視できるほど小さいため、個体群は指数関数的に成長するが、$${N\fallingdotseq{K}}$$の時は成長率が減少し、個体群サイズはKに近づく。
指数関数的成長のコードと以下のロジスティック型成長のシミュレーションコードはGoogle Colabで動く。内的自然成長率が小さい$${(r=0.2)}$$と個体数は環境収容力に収束するが、大きいと環境収容力の周りで個体数が振動したり$${(r=2.2)}$$、不規則に変動したり$${(r=2.7)}$$する。このような挙動は内的自然成長率が大きな昆虫の個体群などで実際にみられる。力学系の分野ではカオスと呼ばれ、決定論的にもかかわらず予測不可能なダイナミクスを生じる機構として研究されており、奥が深い。ぜひr:内的自然成長率やK:環境収容力の値を変えて、結果がどのように変わるかシミュレーションを走らせてみてほしい。
T = 100 # タイムステップ数
# ロジスティック成長のパラメータ
K = 100 # 環境収容力
N0_log = 10 # 初期個体群サイズ(ロジスティック成長)
r_log_values = [0.2, 2.2, 2.7] # 内的成長率(ロジスティック成長)
# 時間配列
time = np.arange(T)
# ロジスティック成長のシミュレーション
plt.figure(figsize=(12, 8))
for r_log in r_log_values:
N_log = np.zeros(T)
N_log[0] = N0_log
for t in range(1, T):
N_log[t] = max(0, N_log[t-1] + r_log * N_log[t-1] * (1 - N_log[t-1] / K))
plt.plot(time, N_log, label=f"ロジスティック成長 (r = {r_log})")
# ロジスティック成長のプロット
plt.title("異なる内的成長率におけるロジスティック成長")
plt.xlabel("時間")
plt.ylabel("個体群サイズ")
plt.grid()
plt.legend()
plt.show()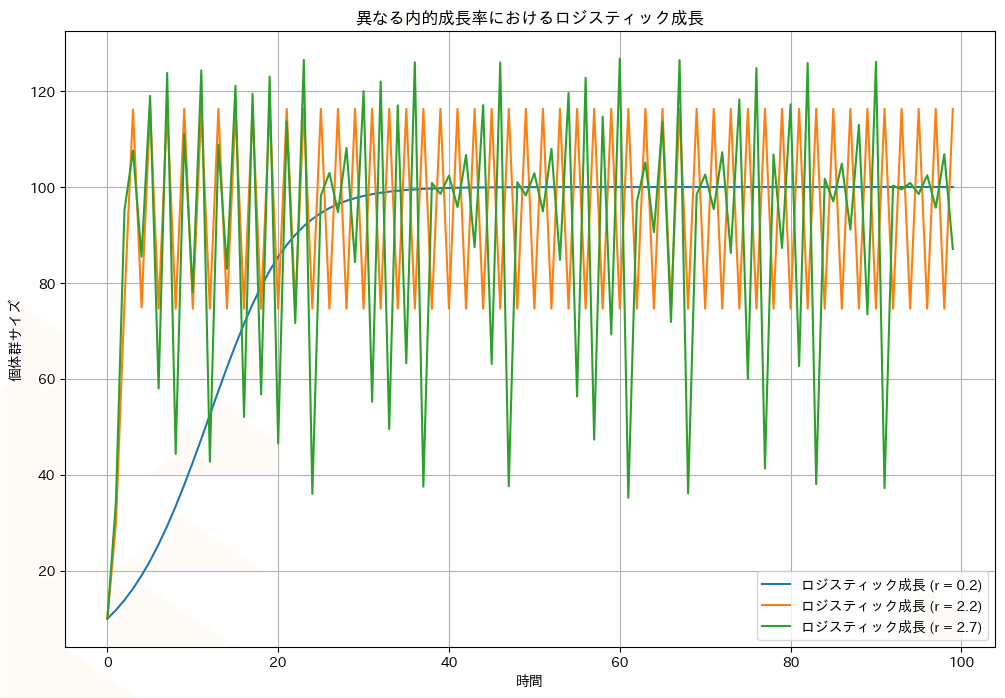
個体群にいる個体数の把握は、種の保全などに重要だが、実際はすべての個体を数え上げるのが不可能な場合が多い。植物などの場合には、ある一定面積の調査区内の個体数を数え上げて個体群密度を算出する方法が用いられる。特定の区画に存在する動物の個体数推定には、一度捕獲した個体に標識をつけて放し、一定期間後に再び捕獲してその中の標識個体の割合から全個体数を推定する標識再捕法がよく用いられる。
種と教師無し学習
生物多様性の基準として生物種を用いることが出来る。真核生物での種の定義に用いられるのが生物学的種概念で、生殖・交配が可能で、生殖能力がある子孫を残せる個体同士を同種と定義する。ただし、この生物学的種概念は無性生殖をおこなう原核生物などには適用できず、それらの生物はゲノムの類似度などが種の分類に用いられる。また、ゲノム解析の結果からホモサピエンスもネアンデルタール人と交配があったことが知られており、動物(ヒト)であっても種の境界は曖昧である。
カール・フォン・リンネは、種の分類、体系化を行った。種の学名は属名と種小名からなり、異なる種はさらに界・門・綱・目・科・属・種と階層的に整理される。例えば、ヒトは動物界・脊索動物門・哺乳綱・霊長目・ヒト科・ヒト属・サピエンス種に分類される。ヒト属には絶滅したネアンデルタール種などが含まれ、ヒト科にはより遠い類縁関係のゴリラ族などが含まれる。この系統関係の推定には現代ではDNA配列解析が用いられることが多いが、リンネの時代からの古典的手法では表現型からの分類が行われる。この分類ではどの種とどの種が近いという正解となるラベルはないが、共有形質の類似度や数から近さが見極められ、クラスターが形成される。これは、まさに教師なし学習による機械学習によって、生物が階層的にクラスタリングされてきたといえよう。
情報理論で測る生物多様性
生物多様性を種を基準として測る尺度として、α多様性、β多様性、γ多様性がある。
α多様性は単一の生態系や局所的なスケールでの種多様性であり、最も簡易的な計算には特定の地域に存在する種数などが用いられる。しかし、種の多様性には種数の他に、それぞれの種の個体数に偏りがあるか、という分布に関する情報も重要そうだ。これを反映して、α多様性の指標には次の式で定義されるシャノン・ウィーナー指数が使われることがある。
$$
H = -\sum_{i=1}^{S}{p_i\ln p_i}
$$
$${H}$$がシャノン・ウィーナー指標、$${S}$$ は種の総数、$${p_i}$$ は i 番目の種の相対的な個体数割合である。
これは、連載の第2回で扱った情報理論におけるエントロピーの概念そのものである。この指標は生態系内で1種をランダムに選んだ際に得られる「情報の平均量」を測定していると解釈でき、種が均等に分布している場合にエントロピーが最大になり、α多様性が高くなる。
β多様性は、異なる生態系間や地点間での種組成の違いを、γ多様性は広域的なスケールでの種多様性を指す。これらも種数(γ多様性)や1-α多様性の算術平均/γ多様性(β多様性)のような簡易的な計算方法のほかに、情報理論に基づく計算手法もあるようだ。
種の絶滅は種に適した環境条件の消失、生息地の破壊などによって起こる。全生物種のうち約75%以上が絶滅した際には大量絶滅と呼ばれ、地球史上で5度の大量絶滅が起こっている。例えば、古生代最後のペルム紀末の大量絶滅では、主に大規模な火山の噴火により陸域と海域の生物の9割以上が数十万年にかけて絶滅したと考えられている。
生物多様性を情報のエントロピーで測ることが出来ることを紹介した。大量絶滅は種の多様性の低下を伴うため、情報の豊かさの消失ともいえる。一度失ったデータは完全には復元できないし、忘却したことは思い出せない。これは誰にでも経験があるだろう。現在の絶滅速度の推定から、議論はあるものの人為的活動により地球史上6度目の大量絶滅が始まっている、または既に大量絶滅の途上にあると考えられている。生物多様性の消失が情報の消失であると思うと、種の保全に対して違った見方ができるかもしれない。
バイオームの主成分
気候は地球上の生態系に最も影響する要因である。地球上の大気循環には太陽エネルギーの入射が大きく影響しており、赤道付近では多量の熱入力に伴う高温により、水が蒸発し暖かい湿った空気が多量の雨を降らせる。一方で、中緯度に移動した乾いた空気は水分を吸収し、乾燥した気候条件を形成する。こうした温度、降水量は植生を構成する植物を中心とした生育する生物のまとまりであるバイオームに影響する。
特に、陸域バイオームについては、年平均気温と年平均降水量を軸にバイオームの成立を大まかに規定することが出来ることが知られており、クライモグラフと呼ばれている。これは、ミクロにみるとそれぞれのバイオームには異なる多様な生物が含まれているにもかかわらず、マクロにはたった2変数の少ない情報量で大まかな景観を予測できるという点で驚異的である。

参考文献
生態学では、種や個体群の相互作用を研究し、生態系の現象を理解する。個体群の成長は、指数関数的成長やロジスティック成長により記述され、環境要因によって変動する。生物多様性やバイオームは、種の分布や気候条件と密接に関係し、情報理論を用いた解析が可能である。
サムネイル画像はDALL-Eにより生成