見出し画像

確変はいつ終わるのか？【スーパービンゴ】

僕のアタマの裏側

今、スーパービンゴは日本各地でまあまあの好評を戴いている。僕個人としては「もうとっくにぱちんこ（少牌確変🌷）を越えてる」と思っている。確変🌷を遊ぶためのルールとしてスーパービンゴはぱちんこよりも遥かに適しているのだ。

全国を回っていい気になって覆面姿で麻雀していると「確変はいつ終わるんだろう」と考える事がある。いや、勿論スーパービンゴは不滅である。でもみんなに尋ねられることがある。「確変はいつまで続くんでしょうか」と。そう、スーパービンゴは結局の所、確変🌷を楽しく遊ぶ為に公案されたルールだ。みんなの関心事は🌷に大きく偏っている。

「この確変、どれくらい続いてどれくらい乗るの？」

こう尋ねられて僕はいつも「まあまあ乗りますし続きます」とだけ答えていた。それくらいアバウトでもいいだろ、どうせ乗る時は乗る。しかし僕の中の誠意と好奇心がこの根源的問いをそのままにする事を許さなかった。計算に勤しむことで、そして解らしき何かを掴んだ。それをこのnoteで共有したいと思う。

通常時の継続率と継続セット数の考え方

牌種の数え方

スーパービンゴでは、牌種は一九を除いて25種となる。しかしここで継続率の分母を25としてはいけない。そもそも一九の代わりに７と⑦が８枚ずつ入っているからだ。27とした上でカバーしていない牌種を引き算していくとわかりやすい。そして6~8の全てをカバーしていない場合はさらに-1とする。まず練習してみよう。

最初に取り沙汰した牌姿

これは①⑨(2種)678(3+1=4種)字牌(7種)が乗らないので27-(2+4+7)=14種乗り。678全てが乗らない時、7が2牌種分乗らない事になるので1種増える事を覚えておこう。

これは字牌(7種)以外全て乗るので27-7=20種乗り。基本的にこの形がとても強く、全ての基準となる。実際に打っている時は20種からの差し引きで数える事が多い。

これは③④⑧(3種)12345(5種)が乗らないだけで27-(3+5)=19種乗り。そう、こんな形でも案外乗る。

通常継続率

継続率(%)=（牌種／27）×１００
によって簡単に求まる。以下に継続率の早見を用意した。

通常時継続率

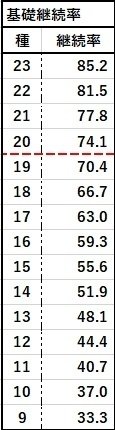
「なるほどー、こんなもんか」という程度のアレである。基準となる20種（筒子索子全乗り）に線を引いておいた。では次に進もう。

継続セット数

継続セット数とは平たく言えば「何回山をめくれるか」の事だ。これは
継続セット数＝転落率の逆数-1
によって求まる。突然転落率というものが出てきたがこれは
転落率(%)=100-継続率
から導かれる。継続セット数を求める時に最後に-1するのはなぜか、については周りのおじさん達にST継続回数の求め方について尋ねればよくわかると思う。

ST駆け抜けは地獄である

転落する最後の一回は🌷が乗らない為、差し引かなければいけないのだ。これについても早見を用意した。

通常時継続率及び継続セット数

「え、こんなもんか？」といった印象ではないだろうか。では実際に求めてみよう。

通常ピンソーフル

この牌姿は筒子索子全乗りなので20種⇒74.1％継続⇒2.9セット乗りであると分かる。また、この牌姿ならば1セット毎平均して2.1枚乗る。これは単純に乗る場合の数え上げだけれど、凡その場合について「平たくなっていればいるほど大体2枚乗りになる」と覚えていてくれれば良い。よって上記牌姿の時は平均すると

2.9×2.1=6.09(枚)

乗りとなる。出和了で6枚、ツモって12枚といった所だ。

上記結果を聞いてみなさん内心こう思ったことだろう。
「あれ、あんまり🌷って乗らないんじゃ…？」
確かにその通りであるし、しかしながらそんなことはないので安心してほしい。そう、これはあくまで通常の場合の話だ。それではみなさんをめくるめく確変の世界へとお連れしよう。

確変時の継続率と継続セット数の考え方

確変継続率及び継続セット数

確変継続率(%)＝[1-{(27-牌種)/27}^2]*100
として求まる。急に込み入った数式になって面食らう諸兄もいるだろうが何の事はない「一度に上下と捲るから、そのどちらかが乗っていれば継続するよ」という事だ。早速だが早見表をご覧いただきたい。

確変時継続率

ご覧の通り、半端じゃない。継続セット数は通常時と同じ方法で求まるのでここに更に記載しよう。

確変時継続率及び継続セット数

20種を超えてからの伸びしろたるや夥しい。では、実際の牌姿に従って考えてみよう。

確変ピンソーフル

これもまた筒子索子全部乗りなので20種、よって93%継続であることがわかる。これは実に大工の源さん超韋駄天と同じ継続率である。「この形は源さん」と覚えると直感として掴みやすい。

では、乗る枚数についてはどうか。ここで僕たちは更に少しだけ面倒な計算をしなければならない。

平均乗り枚数の算出

ここまでで通常時及び確変時における牌種毎の継続率及び平均セット数が求まった。では、導出した二つの表を比較してみよう。

確変時と通常時の比較

こう比較すると、セット数が全く違う事がはっきりとわかる。通常時で最も継続率が高いのは23種である。

筒子索子フルカバー（20種）+字牌（3種）

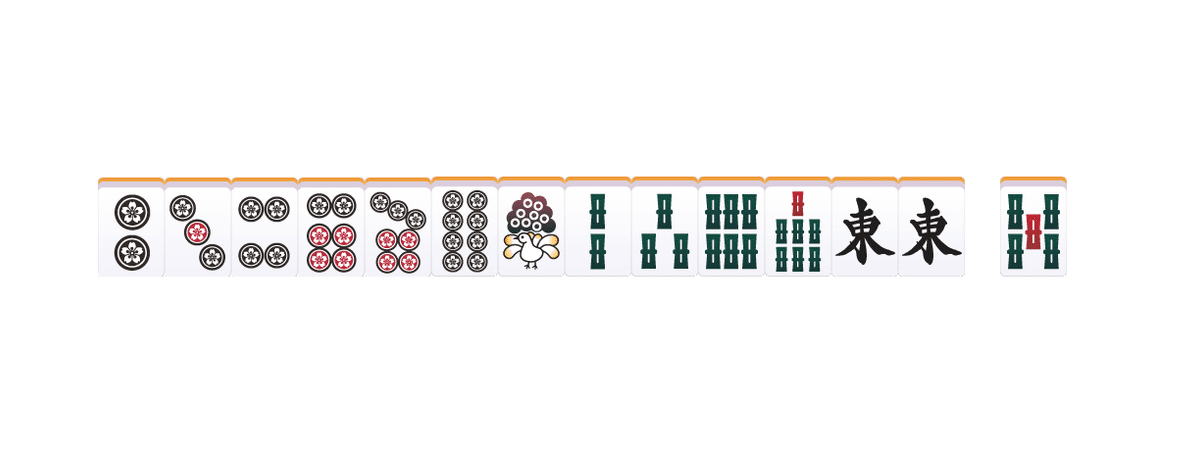
継続率は実に85.2％、🌷を打つ上で目指すべき理想的な形だ。しかしこれは通常の話であって、確変と比較すれば例えば以下のような牌姿にすら継続率で劣る事となる。

筒子索子フルカバーに3種足らない(17種)

では、実際に何枚乗るのかについて先ほど取り上げた牌姿で考えてみよう。

確変ピンソーフル

これもやはり平均乗り枚数を2枚と数えて以下のように

13.9×2.0=27.8(枚)
乗りとなる…とするとこれは誤り。なぜなら1セット毎に上下で加算するからだ。しかしこれで「なるほど、２倍すれば良いのか」として
13.9×2.0×2=55.6(枚)
とするとこれも誤り。簡単に説明すると、継続する場合は
ⅰ.上下共に乗り継続
ⅱ.上だけが乗り継続
ⅲ.下だけが乗り継続
の３パターンが考えられる。この合成によって１セット毎に何回乗るかが求まる。以下に最終的な回数を含んだ表を提示する。

通常時及び確変時の継続回数比較表

という訳で、これからは通常・確変を問わず
平均乗り枚数=平均乗り回数×平均乗り枚数
によってチューリップ枚数を求める事が可能となった。特殊な形（例えば四暗刻系）を除けば平均乗り枚数は2.0と数えて問題ないのでより簡単に
平均乗り枚数=平均乗り回数×2.0
としても良い。

という訳で再計算しよう。

親の顔より見た確変ピンソーフル

22.0×2.0=44.0(枚)
これが答えとなる。勿論この乗り枚数は正規分布に従う為、事故ればこんなもんじゃないし即パンすれば0枚だ。それが醍醐味なのだけれど、やはり僕たちは確かな数字が欲しくなる。

「この確変、どれくらい続いてどれくらい乗るの？」

こう尋ねられた時、僕たちはもう早口でこう答えることができる。
「継続率77%で3.3回続いて、上下合わせて平均して4.5回乗ります。ただし、形が寄っているので凡そ1回あたり3枚くらい乗る(*)ので大体14枚乗りますね」

*ちなみにこの牌姿では計算上の平均枚数は3.2枚なんですよ。平均枚数って実は継続率が下がる程上がるんです。僕クラスになると勘で答えても大体あってるんですよね。

と、このクソくだらないウンチク以上の何かがこの計算結果にあるのだろうか？では、ここからが真の本番であり、しかし余談となる。この数字に基づいて僕たちはどう打牌を判断していくべきだろうか？

ここからはみんなで一緒に考える時間だ

ここから先は

1,839字 / 9画像

¥ 500

期間限定！Amazon Payで支払うと抽選で
Amazonギフトカード5,000円分が当たる

投げ銭いただいた質問には凡そお答え致します。何か気になる事があればチャリンと小銭をお願いします。