
SEND MORE MONEY(覆面算)
アザラシ塾ブログ(https://benkyouhou-kouritu.com/math-puzzle/)でも取り上げましたが、覆面算の有名問題、SEND MORE MONEY問題を解説したいと思います。また今回このブログでは、上記リンクのブログ内で類題として紹介しました、高校入試過去問題3問についても解説いたします。
次の筆算で、各文字には異なる0~9の数字が入ります。
【問題①】各文字に入る数字を解答しなさい。

【問題②】各文字に入る数字を解答しなさい。(日大日吉)
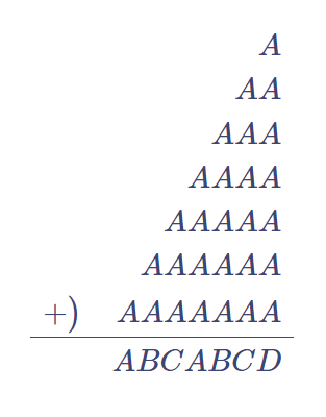
【問題③】各文字に入る数字を解答しなさい。(甲陽学院)
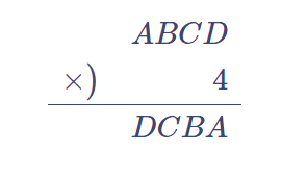
【問題④】各文字に入る数字を解答しなさい。(名古屋)
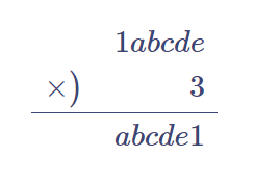
【問題⑤】1)b≧4である理由を述べなさい。2)各文字に入る数字を解答しなさい。(開成)
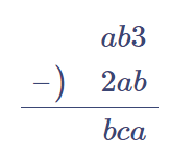
【問題⑥】□内に入る数字を解答しなさい。(2012算数オリンピック)
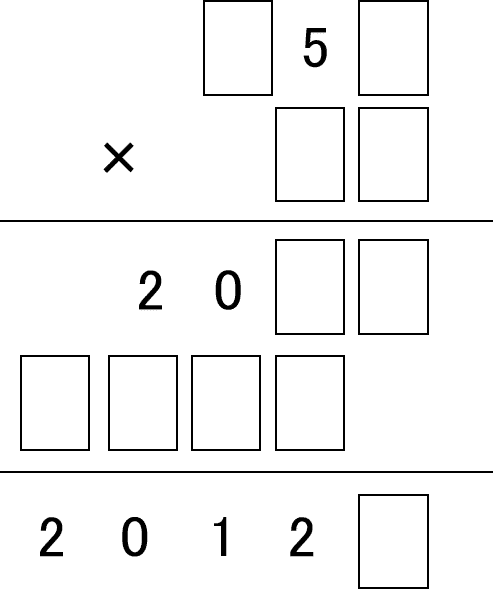
【問題①の解答】
まず、この筆算は4桁+4桁=5桁の筆算です。よって、$${ M \geqq 1 }$$。また、仮に4桁すべての数字が9であったとしても、
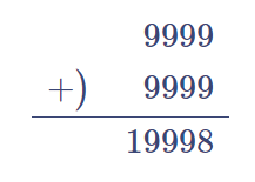
となります。上の例の場合、4桁すべて9に相当する同じ文字で表されている必要がありますが、実際にはそうではないので、$${ SEND < 9999, MORE < 9999 }$$となります。いずれにしても、Mが2以上になることはあり得ません。したがって、$${ M = 1 }$$
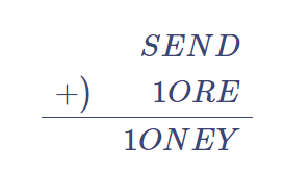
次に、SとOについて考えます。Sは1を加えて、あるいは、繰り上がってきた1をさらに加えて2桁になる数、よってSは8または9。ここで考えられる2桁の数は、$${ 8(S) + 1 + 1 = 10, 9(S) + 1 = 10, 9(S) + 1 + 1 = 11 }$$より、10または11ですが、11ではMとOが同じ数になるので、10しかありえません。 したがって、$${ O = 0 }$$
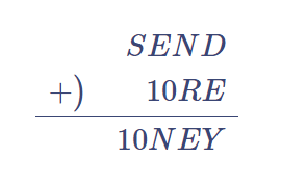
次に、SとEですが、Eは0を加えてNと文字が変わっているので、前の位から繰り上がりを受けて、さらに1足されている必要があります。つまり、$${ E + 0(O) + 1 = N }$$または$${ E + 0(O) + 1 = 10 + N }$$となっている必要があります。2つ目の場合、1足されて10以上となりますが、この場合、あてはまるEは9のみです。しかし、$${ 9(E) + 0(O) + 1 = 10 + 0(N) }$$となり、NとOがどちらも0となるので、成り立ちません。
したがって、Eと0と1を足して、10を超えることはないので、先ほどのSについては、前の位からの繰り上がり無しで、Sに1を加えるのみで2桁となる、$${ 9(S) + 1 = 10 }$$の場合のみ成立することとなります。よって、$${ S = 9 }$$また、$${ E + 1 = N }$$
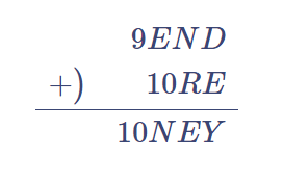
ここで、Eは0,1,9ではないから、$${ 2 \leqq E \leqq 8 }$$N+Rは、2桁でなくてはならない、また前の位からの繰り上がりの可能性もあるから、$${ 11 \leqq N+R \leqq 18}$$N,Rは8以下なので最大は7と8を選んだ場合の15。したがって、$${ 11 \leqq N+R \leqq 15 }$$
①N+Rが前の位から繰り上がりを受けない場合
$${ N+R = 10 + E }$$また、前述の$${ E+1 = N }$$より、$${ E+R+1 = 10 + E }$$ すなわち$${ R = 9 }$$ところが、SとRが同じ数になってしまうため、これは成り立ちません。
②N+Rが前の位から繰り上がりを受ける場合
$${ N+R+1 = 10 + E }$$また、前述の$${ E+1 = N }$$より、$${ E+R+2 = 10 + E }$$ 変形して$${ R = 8 }$$したがって、$${ 11 \leqq N+R \leqq 15 }$$ すなわち$${ 3 \leqq N \leqq 7 }$$ Eに置き換えると、$${ 2 \leqq E \leqq 6 }$$
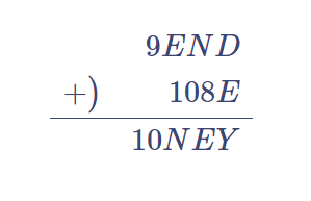
前述の通り、D+Eは2桁の数でなくてはなりません。
a) E=6の場合
D+Eが2桁になるためには、Dは4,5,7のいずれかですが、4,5の場合、Yがそれぞれ、0,1となり、O,Sと同じ数となってしまうため、不適。よってD=7、Y=3。
b) E=5の場合
D+Eが2桁になるためには、Dは6,7のいずれかです。6の場合、Yが1となり、Sと同じ数となってしまうため、不適。よってD=7、Y=2。
c) E=4の場合
D+Eが2桁になるためには、Dは6,7のいずれかですが、それぞれYが0,1となり、O,Sと同じ数となってしまうため、不適。
d) E=3の場合
D+Eが2桁になるためには、Dは7ですが、Yが0となり、Oと同じ数となってしまうため、不適。
e) E=2の場合
D+Eが2桁になるためには、Dは8ですが、Rと同じ数となってしまうため、不適。
これらから、a)b)より、D=7。ここで、E+1=Nなので、a) E=6の場合、実はNもDも7となり不適。したがって、成立するのは、b) E=5の場合のみとなります。
よって答えは以下の通り。
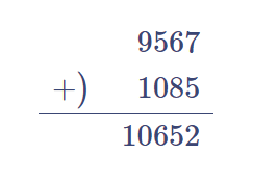
【問題②の解答】
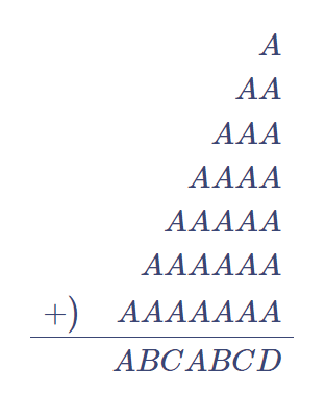
問題②の重要な点として、まず、1桁+2桁+・・・+7桁の筆算の解が7桁の数となっていて、最後に加えられた7桁の最高位の数(100万の位)と、和の解であるABCABCDの最高位の数が等しい、という点があげられます。Aに何かを加えた数の1の位がAとなるのは、
$$
A+X = A, または A+X=A+10
$$
ですが、1つ目の場合、Xは0、つまり繰り上がりは無し、2つ目の場合、Xは10となりますが、上述の通り、和の解の桁数が7桁のままなので、2つ目の場合は成り立ちません。よって10万の位の計算による100万の位への繰り上がりは無し、となります。
よって10万の位の計算は
$$
A+A \leqq 8 \\
\therefore 1 \leqq A \leqq 4
$$
となります。
1) A=1の場合
和の計算で繰り上がりがないので、ABCABCDの各位は全て異なる数となります。A、B、Cそれぞれの位は同じ数である必要があるので、不適。
2) A=2の場合
一の位:2×7=14となりD=4, 十の位:2×6+1=13となり、C=3、百の位:2×5+1=11となり、B=1、千の位:2×4+1=9となり、A=9。よって、A=2の仮定と矛盾するので不適。
3) A=3の場合
一の位:3×7=21となりD=1、十の位:3×6+2=20となり、C=0、百の位:3×5+2=17となり、B=7、千の位:3×4+1=13となり、A=3(成立)、一万の位:3×3+1=10となり、C=0(成立)、十万の位:3×2+1=7となり、B=7(成立)、よって成立。
4) A=4の場合
一の位:4×7=28となりD=8、十の位:4×6+2=26となり、C=6、百の位:4×5+2=22となり、B=2、千の位:4×4+2=18となり、A=8(成立)、よって、A=4の仮定と矛盾するので不適。
よって、3)の場合のみ成立し、$${A=3, B=7, C=0, D=1}$$。
【問題③の解答】
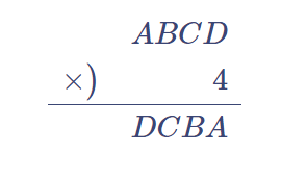
ABCDの4桁の数に4をかけても桁数が4桁と変わっていない。したがって、Aは4をかけて繰り上がってはならない。$${ 4A < 10 \therefore 1 \leqq A \leqq 2 }$$
よってAは1または2。一の位に着目し、4×Dの一の位が奇数となる整数Dは存在しないから、A=1は成り立たず、A=2。
このとき、4×Dの一の位が2となるDは、3および8。
ここで千の位に戻り、繰り上がりの可能性も考慮し、$${ D \geqq 4 \times 2 }$$。Dは3または8なので、D=8。
すると、百の位も繰り上がらないことになり、$${ 4B < 10 \therefore 1 \leqq B \leqq 2 }$$。A=2なので、B=1。
十の位で、4C+3の一の位が1となるため、4Cの一の位は8。これを満たすCは2または7。Aが2なので使用できず、C=7
以上から、$${A=2, B=1, C=7, D=8}$$。
【問題④の解答】
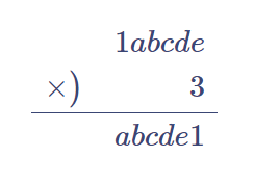
一の位で、$${ 3 \times e }$$の一の位が1となる$${e }$$は 7 のみ。よって、$${e=7 }$$。
十の位で、$${3 \times d+2 }$$の一の位が7となる$${d}$$、すなわち$${3 \times d}$$の一の位が5となる$${d }$$は5のみ。よって、$${d=5 }$$。
百の位で、$${3 \times c+1 }$$の一の位が5となる$${c }$$、すなわち$${3 \times c }$$の一の位が4となる$${c }$$は8のみ。よって、$${c=8 }$$。
千の位で、$${3 \times b+2 }$$の一の位が8となる$${b }$$、すなわち$${3 \times b }$$の一の位が6となる$${b }$$は2のみ。よって、$${b=2 }$$。
万の位で、$${3 \times a }$$の一の位が2となる$${a }$$は4のみ。よって、$${a=4 }$$。
これは、最高位の$${3 \times 1 + 1 = 4 = a }$$も満たす。
したがって、$${a=4, b=2, c=8, d=5, e=7}$$。
【問題④のエレガントな別解】
$${abcde = X}$$とする。題意の筆算は、$${(100000+X) \times 3 = 10 \times X+1}$$と表せる。よって
$$
3 \cdot (100000+X) = 10 \cdot X + 1 \\
3X + 300000 = 10X +1 \\
7X = 299999 \\
X = 42857
$$
したがって、$${a=4, b=2, c=8, d=5, e=7}$$。
【問題⑤の解答】
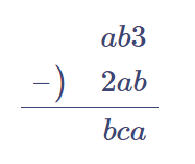
1)$${0 \leqq b \leqq 3}$$とする。このとき、一の位に注目して、$${0 \leqq a \leqq 3}$$。3桁の数$${ab3}$$の百の位は1以上なので、$${a \geqq 1}$$。3桁の数$${bca}$$の百の位も1以上なので、$${b \geqq 1}$$、よって$${3-b=a }$$より、$${a \leqq 2}$$。したがって、$${1 \leqq a \leqq 2}$$。しかしこの時、$${ab3-2ab}$$が3桁の数となり得ない。よって$${b \geqq 4}$$でなければならない。
2) 百の位に着目し、$${a \leqq 9}$$だから、$${b \leqq 7}$$。一の位に着目し、$${b = 4,5,6,7}$$のとき$${a}$$はそれぞれ、$${a=9,8,7,6}$$。$${a=6, b=7}$$のときのみ、十の位の計算で繰り下がりをする必要がなく、$${c=0}$$となる。ただし、この時、百の位の計算、$${a-2=b}$$を満たさないため、不適。よって、十の位の計算は繰り下がりをする計算となり、百の位の計算は、$${a-1-2=b, \therefore a-b=3}$$となる。一の位は、$${13-b=a, \therefore a+b=13}$$となり、これらを連立し、$${a=8, b=5}$$。また$${c=4}$$。
【問題⑥の解答】
便宜上、以下の通り□に番号をつける。

(7)(8)(9)に着目する。(5)+(10)が20を超えることはないから、百の位への繰り上がりは多くても1。よって(9)が最大の9であっても、繰り上がりを受けて足された数の和が11とはならない。よって百の位の計算は(繰り上がりを受ける場合)$${0+0+1=1(この時、(9)は0)}$$か、(繰り上がりを受けない場合)$${0+1=1(この時、(9)は1}$$。いずれにしても千の位への繰り上がりはないため、$${(7)=1, (8)=8}$$。
また、(1)と(4)について、
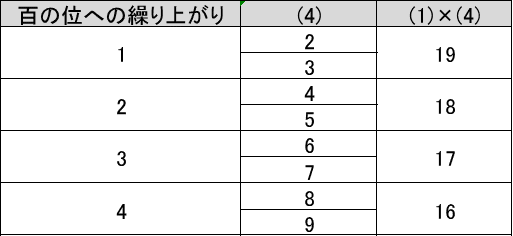
(1)5(2)×(4)の計算を考えた場合、積の千の位が2、百の位が0となるためには、積の百の位への繰り上がりは1~4だから、この繰り上がりと(1)×(4)の和がちょうど20となるためには、上の表から、(1)×(4)=16の時のみ。また百の位への繰り上がりがない場合、(1)5(2)×(4)の積は千の位が2、百の位が0とはなり得ない。したがって、$${(1)=2, (4)=8}$$。(3)については、積の千の位が1、百の位が8であり、$${7 \times 25(2) \leqq 18(9)(10) < 8 \times 25(2)}$$だから、$${(3)=7}$$。
ここで、$${25(2) \times 7 = 18(9)(10)}$$について、$${(2)=8}$$として$${258 \times 7 = 1806}$$となる場合と、$${(2)=9}$$として$${259 \times 7 = 1813}$$となる場合が考えられるが、$${(2)=9}$$の場合、$${(5)+3}$$の一の位が2となるためには、$${(5)=9}$$だが、この時、百の位へ繰り上がってしまい、最後の和の百の位が2となり不適。したがって、$${(2)=8}$$の場合が正しく、この時、$${(2)=8, (9)=0, (10)=6}$$。残りはそれぞれ計算し、$${(5)=6, (6)=4, (11)=4}$$。
