見出し画像

Graphilia入門

AYANO_TFT

※この記事は、VRChat（VRSNSプラットフォーム）で活動する「VRChatワールド探索部」、通称ワ探の部員によるアドベントカレンダー、 #ワ探アドカレ の19日目です。

VRChatには、Graphiliaというワールドがあります。

ワールドの中でシェーダーを作ることができます。
ノードベースで、とても操作しやすいUIなので快適に遊べます。

もっとたくさんの人がGraphiliaで遊んだり、それをきっかけにシェーダーを書いたりしてほしいので、今回はGraphiliaの入門記事を書いてみようと思います。

どれくらい読みやすく書けているかわかりませんが、シェーダーがわからなくても、アバター改変やワールド作成でUnityを触ったことがあるVRChatterであればわかる、というところを目指してみます。

基本操作についてはワールド内にも書いてありますが、以下を抑えておけば良いです。

・頭のうえにあるステッキを掴んだ状態で、右手コントローラーのスティックを上に倒しているあいだ、UIが表示されます。
・数値を変更するとき、スティックを下に倒しながら操作すると0.5刻みで変更できます。

シェーダーと言えば主に色を付けるものですが、Graphiliaにおいてより直感的に理解できて入門に適しているのは頂点シェーダーだと思います。
これはモデルの形状を変えたり、動かしたりすることができます。

なので、まずUIからConfigを開き、Vertex Shader（＝頂点シェーダー）ONを選びます。

※RadeonのGPUを使用している場合はクラッシュしてしまうそうなのでご注意ください。

まずUIがめちゃくちゃかっこいい。

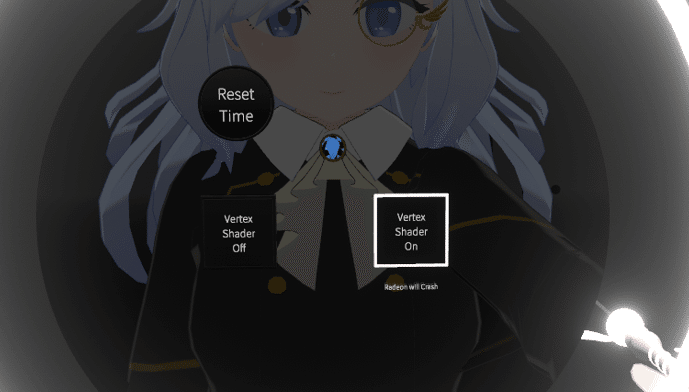
頂点シェーダーで何をするか。

ビームを飛ばします。

たのしい

ビームは作りがシンプルな割に楽しく、基本となる掛け算・足し算がどういった挙動をするのかよく理解することができます。アレンジも色々出来て面白いです。

手順を追っていきましょう。

①元となる球を出す

UIを開き、Outputの中にあるSphereを選びます。
以降、この操作を以下のように書きます。

Output>[Sphere]を出します。

黒い球が出る。

②Local Positionを出す

Input>[Local Position]を出し、先に出した[Sphere]のpositionに繋ぎます。

特に何も変化しません。

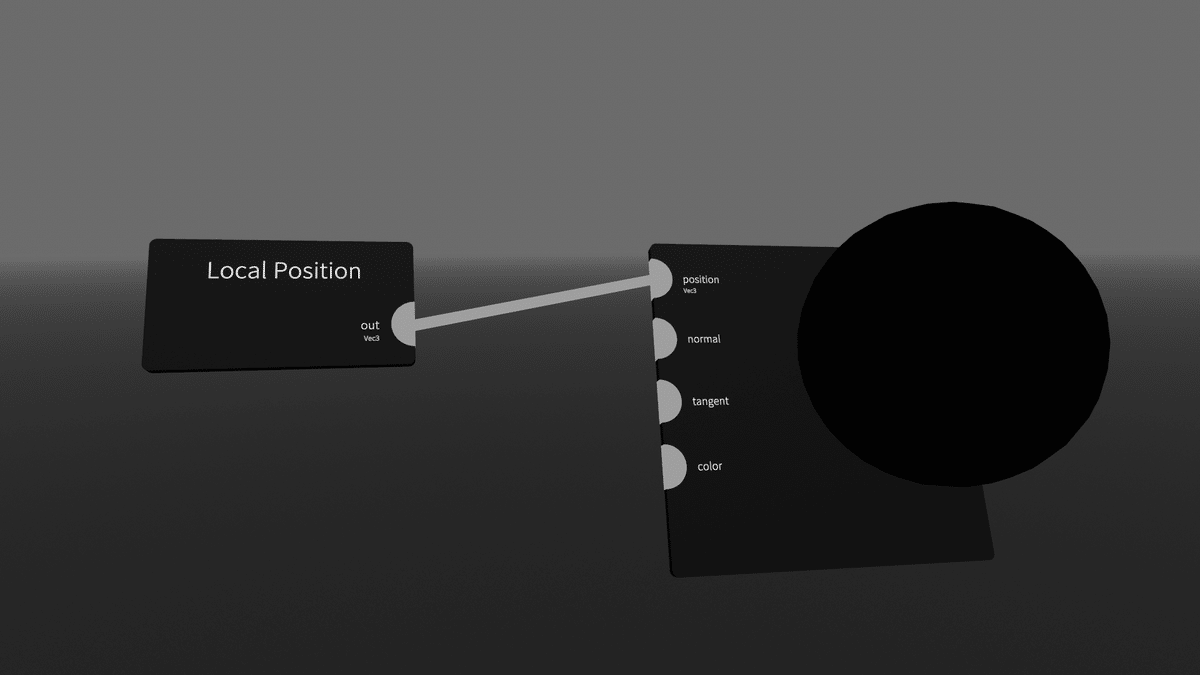
このノードには何が入っているのでしょうか。

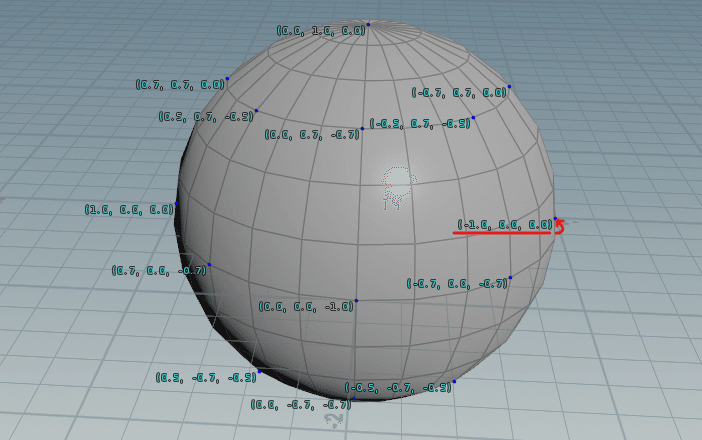
こういう感じの数値が[Local Position]ノードに入っています
例えば右端の頂点は、X=-1, Y=0, Z=0の位置にあります。
※この画面はHoudini、値を表示する頂点や有効桁数は適当に間引いています。

図のように、球の中心を(0, 0, 0)としたときの各頂点の座標がlocal positionには入っています。

③ビームの形状を作る。

Arith>[Mul]
Value>[Vec3]
を出し、[Mul]に[Local Position]と[Vec3]を繋ぎます。
[Vec3]のXは大きい数値（とりあえず10前後）を入れ、他には1を入れます。

さっきまで球だったものが棒のように伸びます。

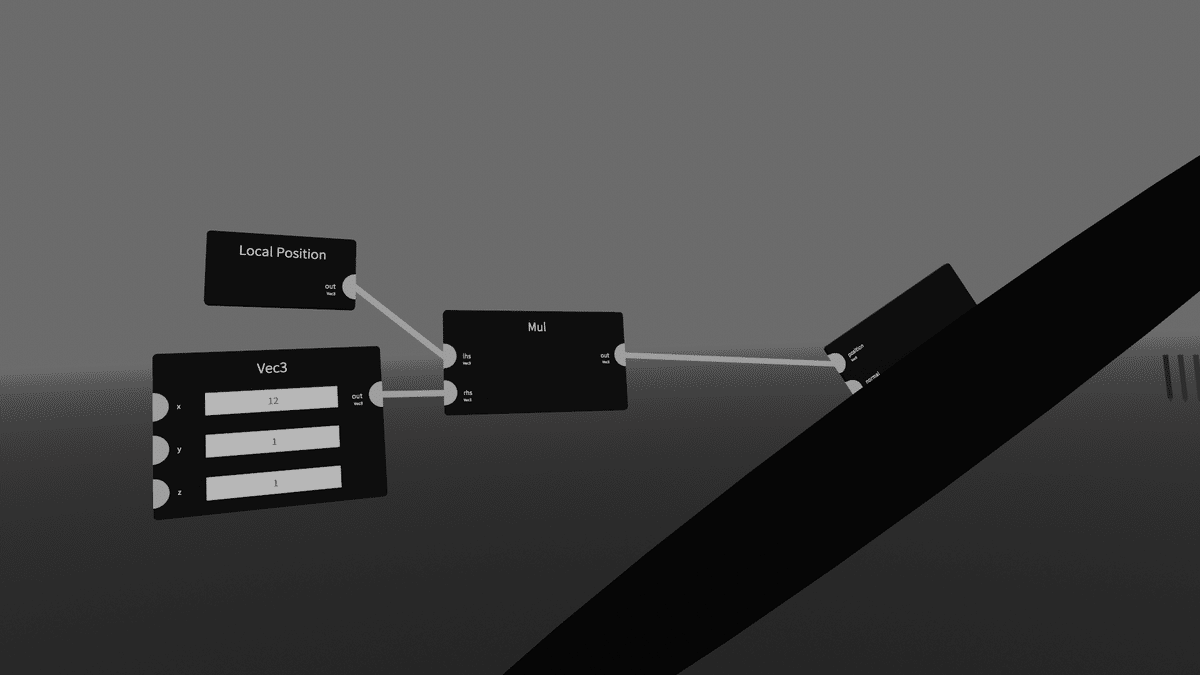
[Mul]は掛け算です。[Local Position]から入ってきたすべての頂点の位置に、[Vec3]の値が掛け算されます。例えば(12,1,1)を入力します。
すると、上の画像で言うところの右端の頂点は（-12, 0, 0）のような位置に移動します。球は左右に伸びます。
高さと奥行きは変えたくないので、YとZには1を掛けます。

(-1,0,0)に(12,1,1)を掛け算した結果の位置に頂点が移動します。
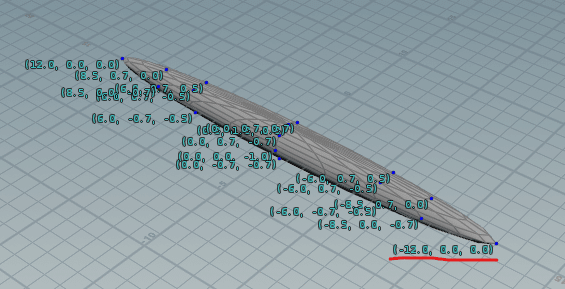
それぞれの頂点に同じように(12,1,1)が掛け算されています。

④移動させる。

一番難しいところです。理解を深めるから進めるために、まずは[Add]、つまり足し算がどういう挙動をするのか確認してみましょう。
Arith>[Add]
Input>[Vec3]
を出し、さっきの[Mul]のあとに繋いでみます。

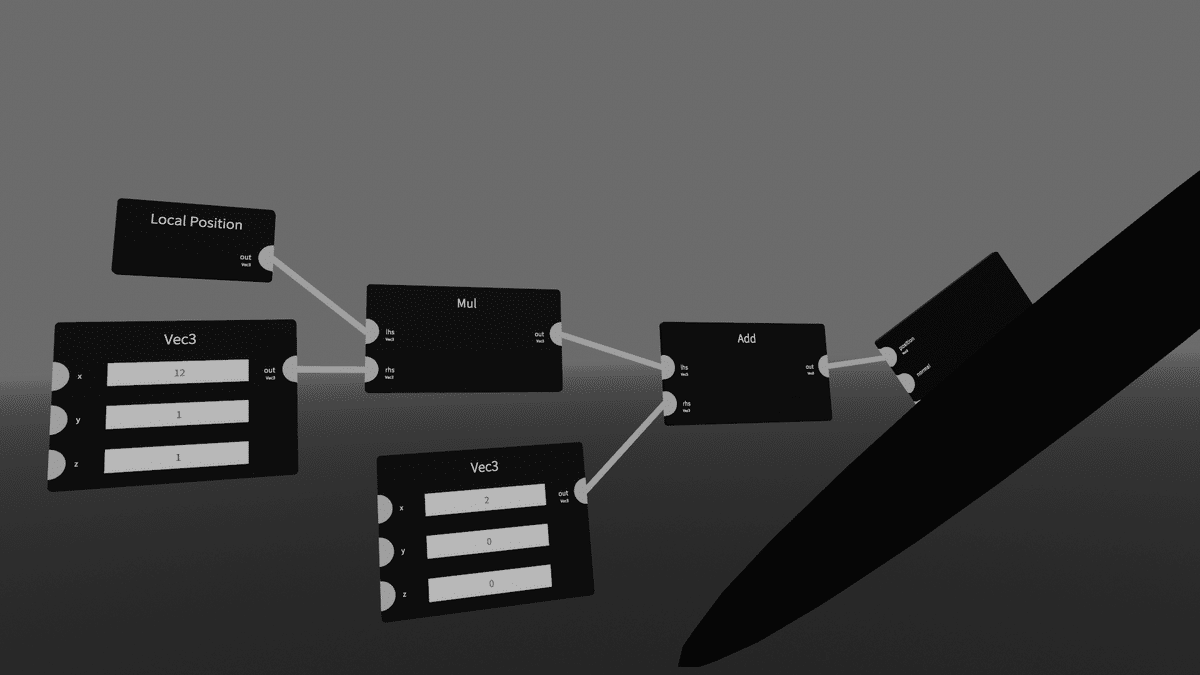
[Mul]と[Sphere]の間に[Add]を割り込ませ、新しい[Vec3]を繋ぎます。

[Vec3]の値を動かしてみると、球が色々な方向に動きます。
全ての頂点に同じ値を足しているので、スライドするように移動するわけです。

Xなら左右、Yなら上下、Zなら前後に移動します。

次に進む前に、[Vec3]の値は(0,0,0)に戻しておきます。

この[Add]を使って、時間経過で球が移動するようにすればビームの動きを作ることができそうです。
Func1＞[Fract]
Input>[Time]
を出し、以下のように繋ぎます。

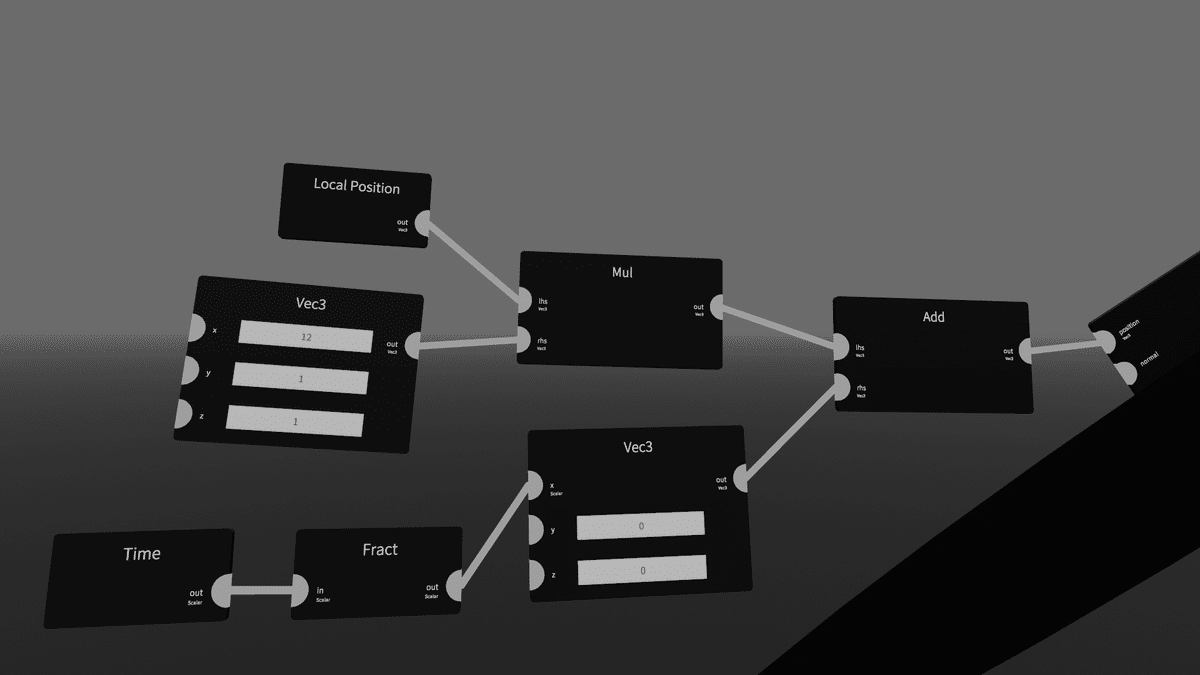
Timeにはインスタンスに入ってからの時間が秒単位で入っています。
時間経過で何か動かすにはこれを使いますが、そのままだとどんどん増えてとても大きな値になってしまいます。5分経ったら300が入っています。

Fractは入力の小数点以下の部分だけを取り出すものです。
1.1なら0.1、5.6なら0.6、0.3なら0.3が返ってきます。

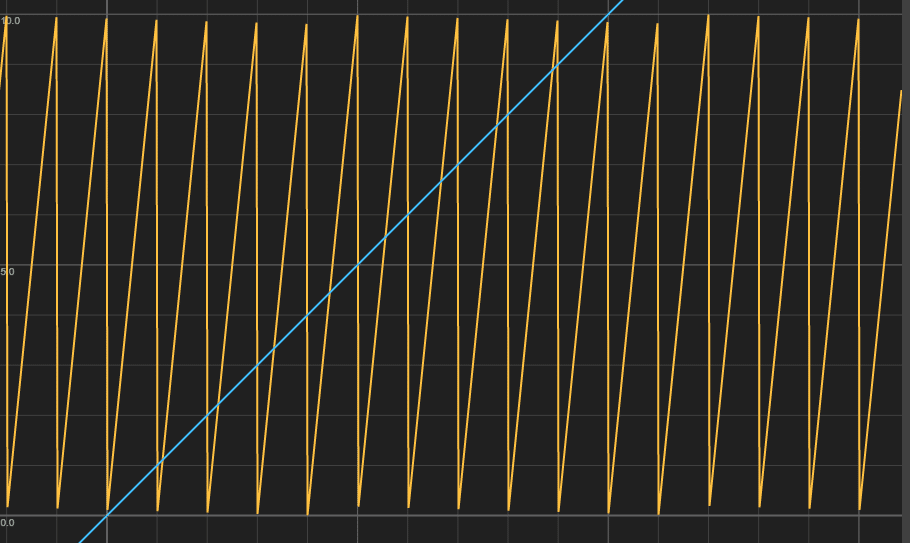
TimeとFractを繋げた結果を言葉で説明するのは難しいので、グラフで示します。
以下の黄色いグラフのように変化する値を取り出すことができます。
青は元のTimeです。
何秒経っても0と1の間の値が取れるようになります。

毎秒0から0.9999に向かって増えて、1秒経つと0に戻る
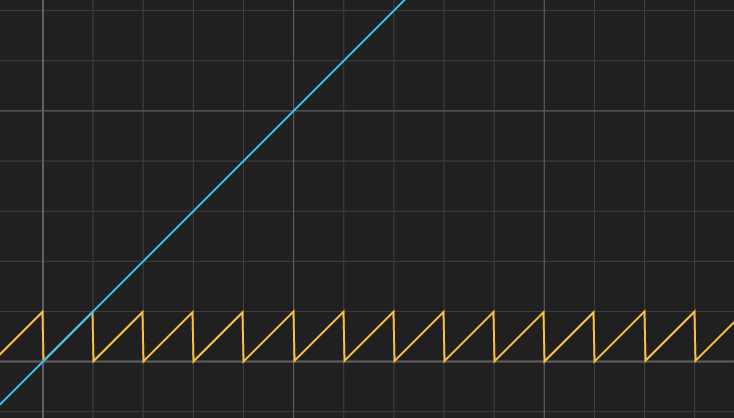
※シェーダーを書くとき便利なgraphtoy.com

これを[Vec3]のxに繋ぎ、[Add]を使ってpositionに足します。
動きます。

まだビームというにはあまりにも遅いです。

⑤早く遠くに飛ばす

今は1秒かけて1しか進まない状態です。ビームらしく早く遠くに飛ばすには、グラフで言うとこうなってほしいわけです。

本当はもっと、毎秒300くらい増えてほしい

Arith>[Mul]を出し、Fractのあとに繋ぎます。
[Mul]の数値を300くらいまで上げます。

よく飛ぶようになりました。

⑥色を付ける

このままだと黒い物体が飛んでいくだけなので、色を付けます。
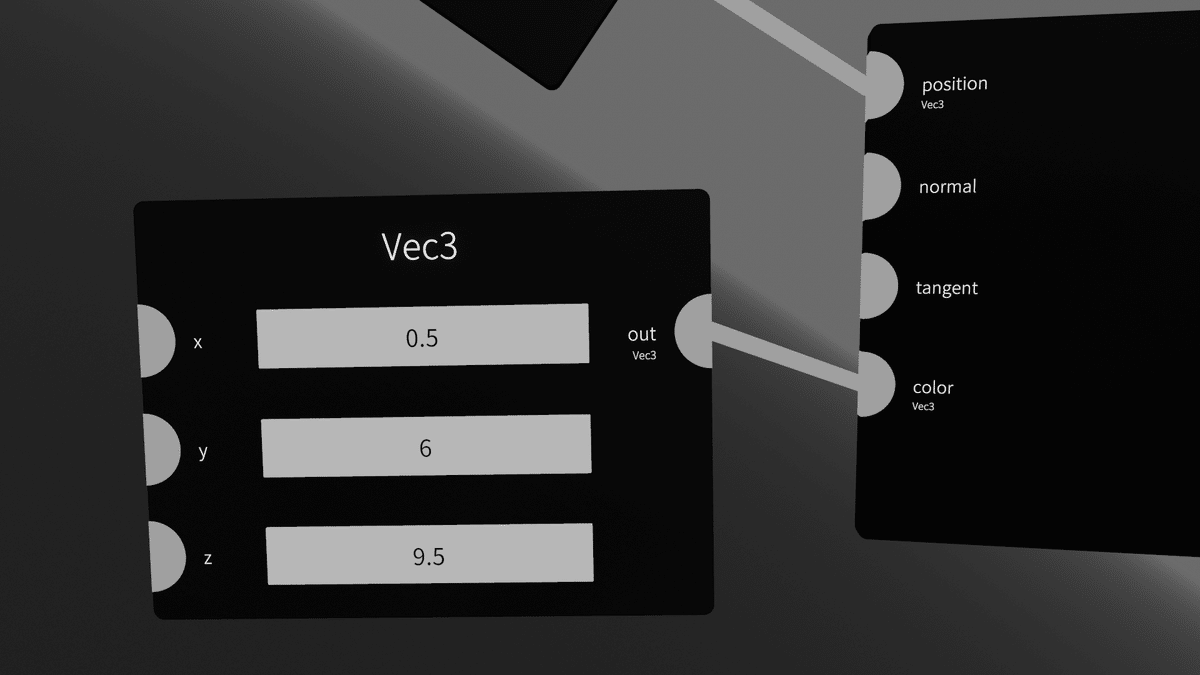
Input>[Vec3]を出し、好きな色を指定して[Sphere]のcolorに繋ぎます。

[Vec3]のxyzがそのままRGBとして使われます。
256段階のほうが慣れている人もいるかもしれませんが、ここでは(0,0,0)が黒で(1,1,1)が白になります。(1,0,0)は赤。
また、1以上が入るとBloomの効果で滲んで見えます。つまり光ります。

ビームは光ったほうが良いので、このように1つか2つに大きい数値を入れるのがオススメです。

⑦完成

速度やビームの長さを好みに調整して、完成です。

完成形のノードはこんな感じ。全部で10個です。

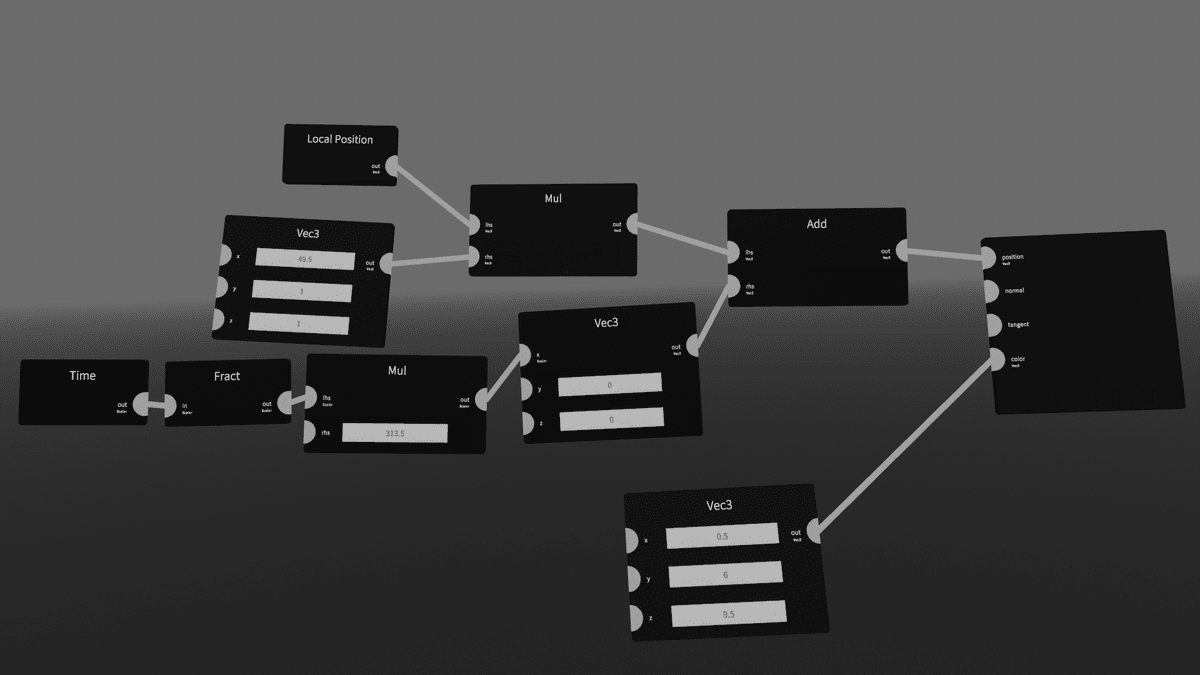
⑧応用

色々とノードを増やして動きがどう変わるか試してみるのも良いです。

形や移動、色などそれぞれの計算をしているノードを跨って繋げるのが面白かったりします。適宜[Mul]で大きさを調整すると良いです。

・[Add]に繋げている値を[Sin][Cos]に通して形状に反映させる

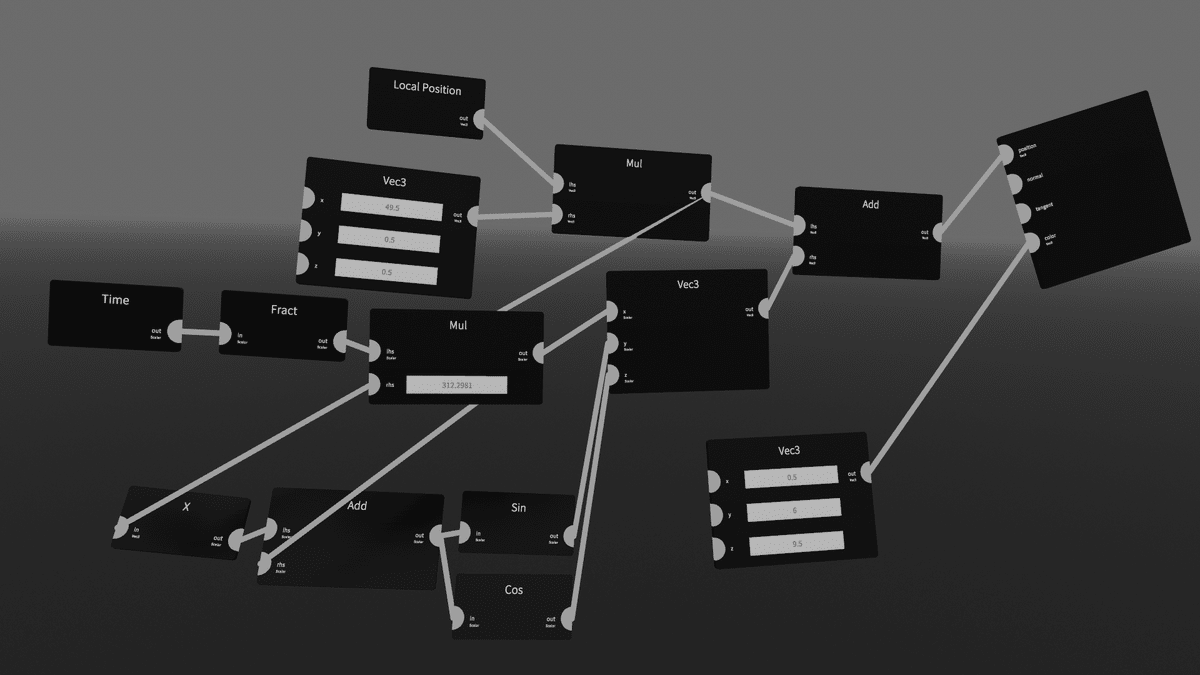
ちょっと難しい。[X]ノードは[Vec3]のx成分だけ欲しいときに使います。
回転しながら飛んでいきます。

・Other>[HSV2RGB]にX座標を繋げると進みながら色が変化する

[Div]は割り算、値の調整に使いました。
いわゆるゲーミングカラー的な。

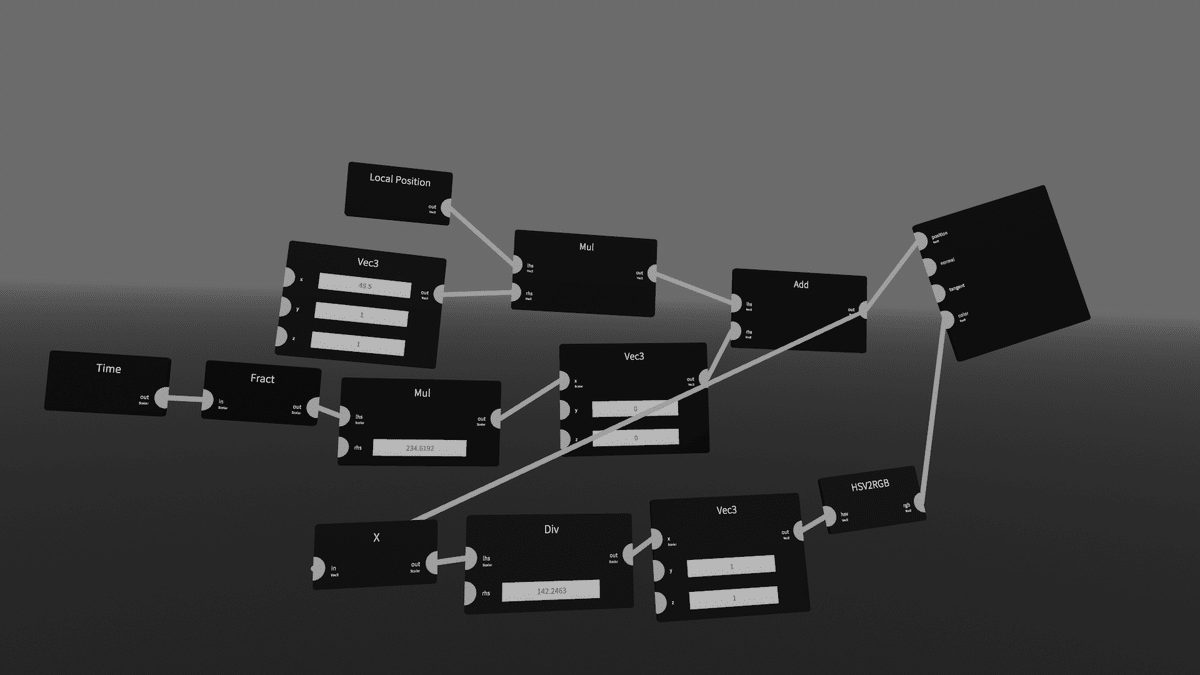
⑨補足

今回はノードベースで主に頂点の座標を操作しました。
全ての頂点に同じ計算が行われる、というのがポイントです。
別々の入力（今回は球の各頂点の座標）に対し、同じプログラムの処理が行われて、その結果を返す。
色の方も似たような考え方で、こちらは各ピクセル（みなさんのHMDの画素）ごとに同じプログラムの処理が行われます。入力には色々使えますが、基本的にはUV座標というものを使います。

おまけ

まったく入門向けでは無いですが、以下のような構成で頂点位置にNaNを繋ぐことでGridを裁断して小さなQuadをたくさん取り出すことができます。

ここから頑張ると蝶を出したり、色々できて楽しいです。

あとがき

シェーダーは難しいです。
私もわからないことばかりですがなんとか書いています。

でも、VRChatでは日々シェーダーを使った面白いワールドやギミックが作られていて、それを目にする機会がとても多いです。
入口の部分を少しだけでも知っておくと、それらを前よりも一歩踏み込んで楽しめると思います。
とても綺麗なものが、意外と単純な作りだったりもします。
本当に分からないすごいシェーダーが出てきて頭を抱えることも多いですが。（"Graphilia"というワールドそのものとか）

ワ探アドカレ、明日はshrさんの「Just a Pool」の解説記事だそうです。
最近の「本当に分からないすごいシェーダー」の一つなので、とても楽しみです。

いいなと思ったら応援しよう！