
ICM, Bubble Factor, Risk Premiumの近似法について
はじめに
ポーカーのトーナメントにおいてICM, Bubble Factor, Risk Premiumの概念は非常に重要な役割を果たしていることが知られているが、一方でこれらはプレイ中に計算不可能な指標であると考えられている。実際、これら指標の厳密な算出は残りプレイヤー数が増えるほど膨大な計算量となり、到底人間の手に負えるものではなくなる。
しかしながら、少なくともプレイ中の意思決定においてはこれら指標の厳密な値が必要となることは稀であり、おおよその値がわかれば十分であることの方が多い。特にICMによる賞金期待値を算出することができればBubble FactorやRisk Premiumも計算可能になるため、賞金期待値の近似的計算手法が重要となる。
そこで本記事では大胆な近似をすることでICMによる賞金期待値をプレイ中に計算できうる計算量に落とし込む方法を考える。特に、「1位の獲得プライズ」「いま飛んだときの獲得プライズ」「プライズ平均」「自身を除いて算出したアベレージスタック」の4つの値からICMによる賞金期待値を近似する。ICMによる賞金期待値は線型性があることと残りプレイヤー数が十分多いときは最後の値はアベレージスタックで近似できることから、この手法は事実上「プライズ平均/1位プライズ」「アベレージスタック」の2つの値から賞金期待値を近似できることを意味する。
このような近似手法について述べた記事は筆者の知る限りでは他になく、例えばGTO Wizardのブログ"ICM Basics"にもこれら指標の重要性を認めながらも"It’s not possible to run ICM calculations in game."という記述があり、賞金期待値の近似的計算手法の導出は一定の価値があると考えられる。
面倒くさい部分(読み飛ばして問題ないです)
1位の獲得プライズを$${P_1}$$, いま飛んだときの獲得プライズを$${P_0}$$, 残っているプライズ総額を残りプレイヤー人数で割った値(プライズ平均)を$${\overline{P}}$$, 自身を除いて算出したアベレージスタックを$${S}$$とする。自身のスタックを$${X}$$とするとき、自分以外のプレイヤーのスタックと各順位のプライズから定まる定数$${A, B, C}$$が存在し、ICMに基づく賞金期待値$${E(X)}$$はその定義式から
$${E(X) = A+\frac{BX}{C+X}+\textrm{higher order terms}}$$
と書ける。
ここで高次項を無視する。明らかに$${E(0) = P_0}$$, $${\lim_{X\to\infty}E(X) = P_1}$$であるから$${A = P_0}$$, $${B = P_1 - P_0}$$。
$${C}$$を決定するために、次のような大胆な近似を行う。すなわち、自身のスタックがアベレージスタック$${S}$$に等しいとき、賞金期待値$${E(S)}$$はプライズ平均$${\overline{P}}$$に等しいとする。$${\overline{P} = P_0 + \frac{(P_1 - P_0)S}{C+S}}$$を解いて$${C = \frac{P_1 - \overline{P}}{\overline{P} - P_0}S}$$
以上のことから
$${E(X) \approx P_0 + \frac{(P_1 - P_0)X}{\frac{P_1 - \overline{P}}{\overline{P} - P_0}S + X}}$$
これが導出したかった近似式である。
検証
前節の計算から、雑に
$${E(X) \approx P_0 + \frac{(P_1 - P_0)X}{\frac{P_1 - \overline{P}}{\overline{P} - P_0}S + X}}$$
と近似されそうだということがわかった。この式の近似精度はどれほどであろうか?簡単に2通りほど検証してみよう。
残り6人、自分以外のプレイヤーをそれぞれ100, 150, 180, 250, 300とし、プライズ配分は1位100, 2位20とする。このとき、自分のスタックを0から600まで変化させたときのICMによる賞金期待値と上の近似式の値は以下のグラフの通りほぼ一致する。
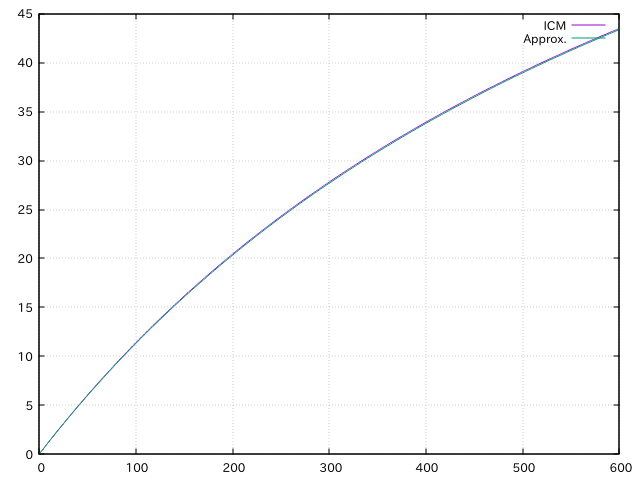
また、同じスタック状況でプライズ配分を1位100, 2位60, 3位40, 4位10としたときのICMによる賞金期待値と上の近似式の値をプロットすると下図のようになり、これも十分な精度でほぼ一致する。

この近似式を用いてBubble FactorやRisk Premiumも計算してみよう。よりFTらしく、プライズを1位100, 2位60, 3位40, 4位25, 5位10とする。自分のスタックが200のとき、300持ちのプレイヤーから受けるBubble FactorおよびRisk Premiumは以下のようになる。
・厳密な値
Bubble Factor = 1.97
Risk Premium = +16%
・近似式から求めた値
Bubble Factor = 1.74
Risk Premium = +14%
Bubble Factorの近似値の誤差がやや大きいものの、実戦的には十分な精度であると考えられる。FTになると例えばBubble Factorの計算において$${\overline{P}}$$を複数回計算しなければならず暗算では少々大変なことになるが、残りプレイヤーが十分多くマネージャンプもないときは後述の通りスタック差分を$${\Delta X}$$として$${\textrm{BF} \approx \frac{D+X+\Delta X}{D+X-\Delta X}}$$と書けるため十分に暗算可能な計算量になる。
現時点でわかっている注意点として、この近似はサテライトバブル等で誤差が大きく使い物にならなくなる場合がある。近似に2次の項を導入することで精度を改善はできるが、それはもはや暗算可能な範囲を超えていると考えられるためここでは詳細は述べない。
追記: Bubble Factorの具体的な近似式
$${E(X) \approx P_0 + \frac{(P_1 - P_0)X}{\frac{P_1 - \overline{P}}{\overline{P} - P_0}S + X}}$$であるから、自分のスタックを$${X}$$、相手のスタックを$${Y}$$としたときのBubble Factorは
$$
\text{BF}\approx\frac{\frac{(P_1 - P_0)X}{\frac{P_1 - \overline{P}}{\overline{P} - P_0}S + X}-\frac{(P_1 - P_0)\max(X-Y,0)}{\frac{P_1 - \overline{P}}{\overline{P} - P_0}S + \max(X-Y,0)}}{\frac{(P_1 - P'_0)\min(X+Y,2X)}{\frac{P_1 - \overline{P'}}{\overline{P'} - P'_0}S' + \min(X+Y,2X)}-\frac{(P_1 - P_0)X}{\frac{P_1 - \overline{P}}{\overline{P} - P_0}S + X}}
$$
となる。
一見複雑に見えるが、実戦的には$${\frac{P_1 - \overline{P}}{\overline{P} - P_0}}$$が一定値とみなせる場合が多く、そのような場合にはかなり計算が簡略化される。
例えばマネージャンプがないとき、あるいは1位プライズに比べていまのプライズが十分小さいときは$${P'_0 \approx P_0}$$である。また残り人数が十分に多いときは$${S'\approx S}$$、誰も飛ばないとき、あるいは残り人数が十分に多いときは$${\overline{P'}\approx\overline{P}}$$である。
従って残り人数が十分多くマネージャンプもないときなどでは$${D=\frac{P_1 - \overline{P}}{\overline{P} - P_0}S}$$として
$$
\text{BF}\approx\frac{\frac{X}{D + X}-\frac{\max(X-Y,0)}{D + \max(X-Y,0)}}{\frac{\min(X+Y,2X)}{D + \min(X+Y,2X)}-\frac{X}{D + X}} \\
=\frac{1-\frac{(X-\min(X,Y))(D+X)}{(D + X-\min(X,Y))X}}{\frac{(X+\min(X,Y))(D+X)}{(D + X+\min(X,Y))X}-1} \\
=\frac{\frac{D\min(X,Y)}{(D + X-\min(X,Y))X}}{\frac{D\min(X,Y)}{(D + X+\min(X,Y))X}} \\
=\frac{D + X+\min(X,Y)}{D + X-\min(X,Y)}
$$
となる。
またRisk Premiumについては、一般的な手法により$${\text{BF}<1.6}$$のとき$${\text{RP} \approx 20(\text{BF}-1)}$$と近似できる。
これら近似式の一例を示そう。WSOP 2023 main event、残り49人、自分のスタックが8.45M、相手のスタックが5.3Mという状況を考える。このとき1位獲得賞金$12.1M、49位獲得賞金$188.4k、プライズ平均$941k、アベレージスタック12.2Mであったらしいから$${D=180.9M}$$、これより上式に代入するとBubble Factor 1.06、Risk Premium +1.4%(一般的手法による近似を用いるなら+1.2%)となる。厳密な計算結果はBubble Factor 1.11、Risk Premium +2.6%であり、恐らくはこれも実戦的には十分な精度であると考えてよいだろう。
この記事が何か役に立つことがあれば嬉しいです。
