
3-A-1【離散数学】数と表現、集合、論理演算の基礎
ブログ教材(コード)一覧
音声解説はこちらのWebページ最上部の▶︎を押してください
バックグラウンド再生も可能です。
【過去問はこちら】どんな問題が出るのか事前に確認しよう!
コンピュータサイエンスや数学の基本的な要素として、2進数の表現、集合論、そして論理演算は非常に重要です。これらの概念は、データの表現や操作、情報の処理において不可欠な役割を果たします。本記事では、これらの基本的な考え方とその利用方法について、順を追って解説します。
1. 2進数の表現と基数変換
2進数の表現
2進数(バイナリ)は、数値を0と1の2つの値を使って表現する方法です。コンピュータでは、すべてのデータや命令が2進数で表現されています。
2進数の特徴
0と1:2進数は、0と1だけを使って数を表します。例えば、10進数の「5」を2進数で表すと「101」となります。
桁の増加:各桁は、2の累乗に対応します。例えば、2進数「101」は、次のように解釈できます。
1 × 2^2 + 0 × 2^1 + 1 × 2^0 = 4 + 0 + 1 = 5(10進数)
基数変換
基数変換は、異なる進数の間で数値を変換する方法です。2進数、10進数、16進数などの異なる基数の間での変換がよく行われます。

基数変換の方法
10進数から2進数への変換:10進数の数を2で割り、その余りを逆順に並べることで2進数を得ます。
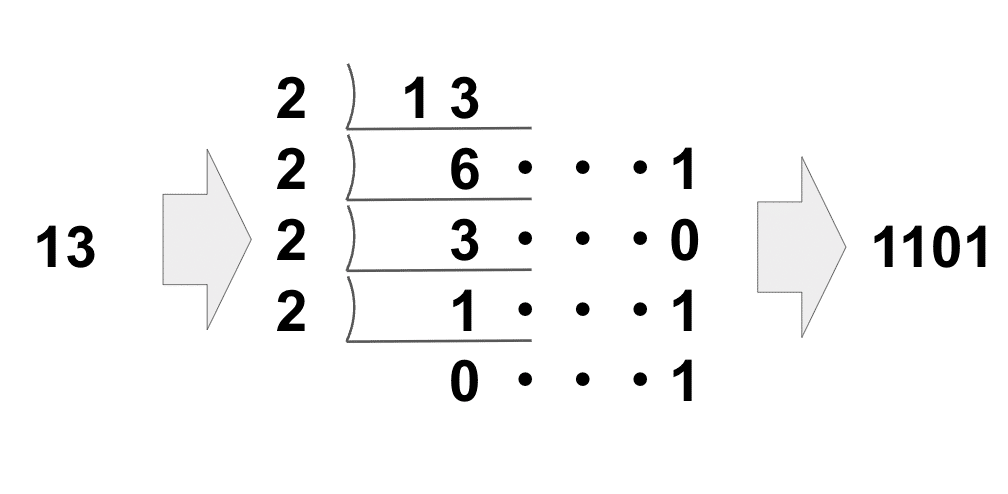
例:10進数「13」を2進数に変換する方法
13 ÷ 2 = 6 余り 1
6 ÷ 2 = 3 余り 0
3 ÷ 2 = 1 余り 1
1 ÷ 2 = 0 余り 1
余りを逆順に並べると、「1101」となります。

2進数から10進数への変換:2進数の各桁に対応する2の累乗を掛け、すべての結果を足し合わせます。
例:2進数「1101」を10進数に変換する方法
1 × 2^3 + 1 × 2^2 + 0 × 2^1 + 1 × 2^0 = 8 + 4 + 0 + 1 = 13(10進数)

2進数の加算と減算
加算
2進数の加算は、10進数と同じく繰り上がりを考慮します。加算のルールは以下の通りです。
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10(繰り上がり)
減算
2進数の減算は、10進数の減算と同じく借りることを考慮します。例えば、10進数で「5 - 3」を計算するのと同じように、2進数でも借りることで減算が行われます。
2. 集合と命題
集合と命題
集合は、特定の要素が集まった集まりで、数学や論理学で広く使われます。例えば、1から5までの数字の集合は{1, 2, 3, 4, 5}です。命題は、真または偽を判定できる文で、集合に関連して、特定の要素が集合に含まれているかどうかを調べることができます。
ベン図
ベン図は、集合の関係を視覚的に表現する図です。複数の集合の共通部分や違いを示すのに便利です。
真理値表
真理値表は、命題の論理的な真偽値を列挙した表で、命題の組み合わせがどのような結果になるかを示します。
3. 論理演算とその利用
論理演算の基本的な考え方
論理演算は、命題の真偽値を操作するための演算です。主な論理演算には、AND、OR、NOT、およびXOR(排他的論理和)があります。
AND(論理積)
両方の命題が真でない限り、結果は偽です。
例:A AND B の場合、AとBが両方とも真のときのみ結果は真。

OR(論理和)
ORは「AもしくはB」を意味します。2つの条件のうち、少なくともどちらかを満たしているデータを検索/抽出するときに利用する条件指定方法です。ORは論理和ともいいます。
少なくとも一方が真であれば、結果は真です。
例:A OR B の場合、AまたはBが真であれば結果は真。

NOT(論理否定)
NOTは「〜ない」という否定の条件をつけることができます。3年生だが、「運動部には所属していない」学生を検索/抽出したいときは、NOTを使います。NOTは否定ともいいます。
命題の真偽を逆転させます。真なら偽、偽なら真になります。

XOR(排他的論理和)
片方だけが真であれば、結果は真です。両方が真か両方が偽の場合、結果は偽です。
真理値表の利用方法
真理値表を使うと、複数の命題がどのように組み合わさった場合に結果がどうなるかを視覚的に確認することができます。例えば、ANDやOR演算の組み合わせを示すことができます。
サマリー
ここから先は

3-A 基礎理論【テクノロジ系】
このマガジンでは、基礎理論に関する重要なテーマについて解説しています。具体的には、離散数学、応用数学、情報に関する理論を取り上げ、情報処理…
この記事が気に入ったらチップで応援してみませんか?
