
再帰的プログラミングと直交多項式
今回初めてこれまでにプログラミングで学んだことについて書いてみます。以下で出てくるコードはいずれもPython3のものです。
プログラミングにおける「再帰」「ループ」と、「ルジャンドル多項式」と言った用語のいずれかを知っている方に読んでいただければ嬉しく思います。ただしこの時点で何をしたか察しのつく方にとっては新しく知る情報は少ないかもしれません。
今回の話題はこちらの書籍で学んだことが元になっています。
1. 再帰呼出し
プログラミングにおいて再帰といえば関数を実装する中で自分自身を呼び出すような手法を指します。またそのようにして実装された関数を再帰関数と呼びます。
再帰を利用する例として分かりやすいのが数学における「階乗」です。負でない整数nに対し、nから始めて1までの自然数を乗じたものをnの階乗(英語ではfactorial)といい、n!のように書きます。例えば
3! = 3・2・1 = 6
4! = 4・3・2・1 = 24のようになります。また特別なものとして0と1の階乗は1であるとされています。
0! = 1! = 1定義より、nが1より大きい場合には明らかに
n! = n・(n-1)!が成り立ちます。したがってプログラムでは、
・nが1以下の場合には1を
・そうでない場合には「n」と「引数をn-1とした自分自身」との積を
それぞれ返すような関数を定義すれば、これが整数型の引数に対してその階乗(※)を出力してくれます。このような具合です。
def factorial(n=1):
if n<=1:
return 1
else:
return n*factorial(n-1)最後の一行が再帰呼び出しになっています。これで任意の整数の階乗をPythonで計算できるようになりました。
※ 細かいことを言いますと上の関数ではnが負のときにも1を返すようにしていますが負の整数の階乗は存在しません。数学には整数でない値に対しても定義できるよう階乗を拡張したガンマ関数がありますが、引数が負の整数である場合にはガンマ関数もまた発散してしまって決まった値がありません。そのため本来階乗を計算する関数ではnが負であればエラーないし警告を出すようにすべきです。実際Pythonのmathライブラリには階乗を返す同名の関数があって例えばfactorial(-1)を計算させようとすると
ValueError: factorial() not defined for negative valuesのようにエラーになります。
再帰的な手法を使えばフィボナッチ数を出力させることもできます。フィボナッチ数列とは、
・初めとその次の項が1
・それ以降は直前の2項を足し合わせた数
からなる数列であり、その一つ一つの整数をフィボナッチ数といいます(最初を0とする定義もあります)。初めの10個を挙げると
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55] といった感じです。フィボナッチ数を返す関数は、その定義そのままに
def fibonacci(n=1):
if (n==0) or (n==1):
return 1
else:
return fibonacci(n-2)+fibonacci(n-1)として実装することができます。この中でifの次の行が「初めとその次の項が1」であること、elseの次の行が「それ以降は直前の2項を足し合わせた数」となることを意味します。これも再帰関数です。実際にこれで例えばfibonacci(7)を呼び出してみれば21という結果が返ってきます。
2. メモ化
論理的には上記のやり方で階乗やフィボナッチ数を計算することはできますが、計算のアルゴリズムの観点からすると賢い方法ではありません。
1つのフィボナッチ数を計算するためにそれより小さい2つのフィボナッチ数を求めるわけですが、それぞれのフィボナッチ数を求めるのにも同じ計算を行う点に注目します。
例えばfibonacci(10)を計算するにはfibonacci(9)とfibonacci(8)とを求めて足し合わせます。そしてfibonacci(9)を求めるときにもfibonacci(8)が必要であるためfibonacci(8)は2回計算されます。これより小さいfibonacci(7)は3回計算されます。このように元の引数(この場合は10)より2以上小さい番号のフィボナッチ数を求める処理が複数回繰り返されることになります。
引数nが3とか5のように小さければ大した問題になりませんが、引数nがある程度以上大きいと、関数を呼び出して変数の型を調べて積や和を計算して代入して... といった演算が行われる回数が非常に多くなってしまいます。これは指数関数的な増大です。
アルゴリズムの教材においてフィボナッチ数の例題はこのような再帰関数の問題を認識するためための位置付けで、『Pythonではじめるアルゴリズム入門』では計算を高速化するために「メモ化」を行いました。これは一度計算して出た結果を保存しておいて後で呼び出すというやり方で、こうことで同じ計算の繰り返しを避けることができます。具体的には次のようにします。
mem = {0: 1, 1: 1}
def fibonacci(n=1):
if n not in mem:
mem[n] = fibonacci(n-2)+fibonacci(n-1)
return mem[n]最初に初めの2つのフィボナッチ数でmemなる辞書(連想配列)を作っておき、欲しい結果がその中にあればその値を返すし、なければそこで初めてフィボナッチ数を計算して登録(メモ)します。ここで登録された数は、より大きなフィボナッチ数を求めるときに再帰で呼び出されます。この方法ならば計算回数がぐっと削減されるため、nが30以上でもほとんど待つことなくfibonacci(n)を得ることができます。
3. ループ
同じ計算をするのにそもそも再帰ではなくループを使う方法もあります。
def fibonacci(n=1):
mem = [1, 1]
for k in range (2, n+1):
mem.append(mem[k-2]+mem[k-1])
return mem[n]ここでは
・memをリストとして最初に初めの2つのフィボナッチ数を入れる。
・3個目以降を求める場合には3項目以降を計算して末尾に追加していく。
・リストの末尾に入った整数を返す。
といったことを行っています。これでもまたメモ化と再帰による手法と同程度の計算量で結果が得られます。
4. ルジャンドル多項式への応用
ここまで知ったところで元物理学科の私はルジャンドル多項式を自分で実装してみたくなりました。
ルジャンドル多項式P_l (x)とは整数パラメータlを持ち -1 ≦ x ≦ 1 の範囲で定義されるxのl次式で、元々は

のように左辺の関数をtで展開したときに現れる係数として考えられました。今日では左辺の関数をルジャンドル多項式の母関数と呼びます。このときxの関数であるP_lは
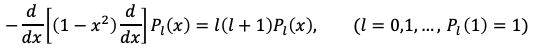
といった微分方程式と境界条件を満たしていて、その表式は
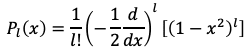
というロドリゲスの公式で求められます。
これが何に使われるのかといいますと、まずクーロンの法則にあるような「逆二乗力」のポテンシャル関数を考えた際に先ほど母関数と呼んだのと同じ形の数式が現れます。より一般には、3次元のラプラス方程式、ヘルムホルツ方程式、ポアソン方程式を球座標(3次元極座標)で変数分離した際の解の一部分がルジャンドル多項式であるので物理学では応用範囲がとても広いです。
物理学科でなくても電子軌道の図を見たことがあれば、あの形を決めているのがルジャンドル多項式から派生した3次元球面調和関数なので応用先の一つを知っているわけです。
このようにルジャンドル多項式とはざっくり言ってこの世の中に電気が存在して空間が3次元であるために物理や化学で必要になる関数であると思えば間違いありません。このルジャンドル多項式をPythonを使って自分で実装してみようという話でした。
実はルジャンドル多項式には帰納的な式
![]()
があり、この中の3つ目はボネの漸化式と呼ばれます。フィボナッチ数をリストとループで求めるプログラムを知ったとき、私にはこの式が思い浮かびました。ここまで考えれば難しいことはありません。
def legpoly(x=1.0,l=0):
mem = [1.0, x]
for k in range(2,l+1):
y = ((2*k-1)/k)*x*legpoly(x, k-1) - ((k-1)/k)*legpoly(x, k-2)
mem.append(y)
return mem[l]関数名は英語のLegendre polynomialsを略して付けています。ここでは
・memをリストとして最初にP_0 = 1.0 とP_1 = x を入れておく。
・l=2以降の項を求めるには漸化式で計算して末尾に追加していく。
・リストの末尾に入った数を返す。
といったことをしています。基本的な考え方はフィボナッチ数列のときと同じで、異なるのは整数のインデックスlの他に浮動小数点型の変数xがあることくらいです。早速この関数を用いてmatplotlibでグラフを描いてみました。

同じような図は検索すればたくさん出てきますが、こうして自分の手を動かしてプログラムを書き、そして図示した結果を見て初めて使える知識として身についた気になります。
私がルジャンドル多項式の出てくる講義を受けたのはもう10年も前のことです。当時はその数式の煩雑さに惑わされた上に勉強にほとんど身が入らなくなっていましたので、レポート課題を提出して単位を取っても何が何だかさっぱり分かりませんでした。
昨年個人的にこうした基本的な「特殊関数」を勉強し直したことでようやくある程度自在に数式を操れるようになりました。これはこれで面白いですが、10年前にもっと積極的になってこういう勉強ができていればどれほど良かったかと思います。本当に「大学生が個性を身につけたければ勉強すれば良いという話」です。
5. その他の直交多項式
こうして味を占めるとせっかくなので他の特殊関数も作ったろかという気分になりました。要は整数のパラメータを持ち、(微分を含まない)漸化式が分かっている直交多項式なら同じ手法で作れるわけです。整数型の変数(物理学における量子数やモードの番号)はリストのインデックスに使い、浮動小数点型の変数(物理学における一般化座標)は四則演算で処理します。そうやって構成できるものを2つ紹介します。
一つはエルミート多項式で、次のように関数prbherpolyを作りました。
def prbherpoly(x=0.0, n=0):
mem = [1.0, x]
if n > 1:
for k in range(2, n+1):
y = x*prbherpoly(x, k-1) - k*prbherpoly(x, k-2)
mem.append(y)
return mem[n]但しこれは物理の教科書に載っているエルミート多項式ではなく、英語版Wikipediaでいうprobabilists' Hermite polynomials、つまり確率論におけるエルミート多項式で、 物理学に出てくるそれとは変数変換と定数倍とで移り替わることができます。この多項式は
![]()
なる漸化式で求められるのでこれを元に実装しました。

もう一つはラゲールの陪多項式です。正確には日本語版Wikipediaにあるものではなく英語版のGeneralized Laguerre polynomials (一般化ラゲール多項式)の方です。実数変数x、インデックスnの他に実数パラメータαを持ちます。これについては
![]()
という少し長い公式を用いることになりましたがやることは同じです。
def genlagpoly(x=1.0,n=0,a=0.0):
mem = [1.0, 1.0+a-x]
for k in range(2, n+1):
y = (float(2*k-1)+a-x)/k*genlagpoly(x, k-1, a)
- (float(k-1)+a)/k*genlagpoly(x, k-2, a)
mem.append(y)
return mem[n]このようにして自分たちの環境でいつでも簡単に直交多項式を出力できるようになりました。
6. 水素原子の波動関数
ラゲールの陪多項式は量子力学の水素型原子のシュレーディンガー方程式の解の一部になっています。詳細は省きますが、変数分離を行い動径の長さrに依存する成分を取り出すと、
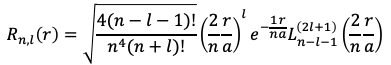
がその(常微分方程式の)解になっていて、右辺の端にある大文字のLがラゲールの陪多項式です。但しn=1,2,...であり、l=0,1,...,n-1という整数に限ります。これらはそれぞれ主量子数、方位量子数と呼ばれます。
また、定数aはその原子のボーア半径で関数genlagpolyの引数aとは別物です。動径の長さrをボーア半径aで割っているので、ρ=r/aは「ボーア半径の何倍の距離か」を表します(参考:原子単位系)。
上記の関数R_n, lは既に規格化されており
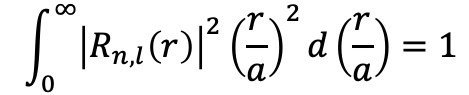
が成り立ちます。先ほどの日本語版ウィキペディアのページにも同じ表記の関数R_n, lがありますが、上記のものとは定数倍だけ異なります。なぜ積分の変数をrではなく無次元量のρ=r/aにしたかというと、この後で異なる固有状態の波動関数の形を比較しやすくするためです。
Pythonではρ=r/aを"rho"(ギリシャ文字ρのこと)として、先ほどの関数genlagpolyと階乗関数factorialを使い新しい関数を定義しました。これは1になる上記の積分の中の被積分関数(integrant)です。
"""
factorialとgenlagpolyをimport
"""
def integrant(rho=0.0, n=1, l=0):
if n > l:
coef = 4*factorial(n-l-1)/(n**4*factorial(n+l))
vari1 = np.exp(-rho/n)*(2*rho/n)**l
vari2 = genlagpoly(2*rho/n, n-l-1, float(2*l+1))
return coef*(rho**2)*(vari1*vari2)**2
else:
return 0.0ここに2つの量子数の組(n, l)を与え、例えば
import matplotlib.pyplot as plt
import numpy as np
(中略)
x = np.linspace(0.0, 25.0, 200)
y = integrant(x, 2, 1)としてx, yをmatplotlibでプロットすれば、電子が原子核のある中心からrとr+drの間の距離にある確率
![]()
をdr/aで割った確率密度の分布曲線を見ることができます。ただ一通りの(n, l)の組み合わせだけ見ても面白くないため、まず(n, l)=(1, 0), (2, 0), (3, 0)の3通りを比較します。これらはそれぞれ1s, 2s, 3sと呼ばれる電子軌道のものです。

このように方位量子数が等しければ、主量子数が大きいほど電子の波動関数が中心から離れた領域に分布することが見て取れます。
(n, l)=(3, 0), (3, 1), (3, 2)でも同様の比較をしました。これらはそれぞれ3s, 3p, 3dと呼ばれる電子軌道に対応します。このように主量子数を揃えて比較すれば、方位量子数が大きいほどピークが中心に寄る様子が伺えます。

先ほどのヨビノリ動画を見るときなんかにこうした定性的なイメージを持っていると分かりやすいかもしれません。もし他の電子軌道も見てみたい方がいましたら、ご自身の環境で関数genlagpolyおよびintegrantを利用し別のパラメータを使ってプロットしてもらえればと思います。但し全ての内容は第三者のチェックを受けたものではなく未だ誤りがあるかも分かりませんので正しさの保証は致しかねます。

関数integrantを規格化したため、いずれ曲線でもy=0の横軸との間の領域の面積を求めれば1になります。それ故これらの曲線は確率密度を表しているといえます。念のため正しく規格化されているか確かめるために、有限なステップ数・有限な長さの区間で数値的に積分を求める関数norm_hydatomを追加し、原点(rho=0)からボーア半径の50倍の距離までの区間においてステップ数500で計算してみました。ここでの出力pとは「(n, l)で指定された電子軌道に対応する固有状態にある電子が原点からボーア半径の50倍の距離までの領域に存在する確率」になります。
(略)
def norm_hydatom(n=1, l=0, radi=50.0, step=500):
integ = 0.0
if l < n:
drho = radi/step
for s in range(0, step):
rho = radi*s/step
integ += integrant(rho, n, l)*drho
return integ
for n in range(5):
for l in range(n):
p = norm_hydatom(n,l)
print('P = '+str(p)+' for n ='+str(n)+', l = '+str(l))その結果は以下の通りです。
P = 0.9999933544529871 for n =1, l = 0
P = 0.9999991684835401 for n =2, l = 0
P = 1.000000000165054 for n =2, l = 1
P = 0.999999698937952 for n =3, l = 0
P = 0.9999999691434047 for n =3, l = 1
P = 0.9999999920869674 for n =3, l = 2
P = 0.99904809636214 for n =4, l = 0
P = 0.9993203497043445 for n =4, l = 1
P = 0.9996795120816482 for n =4, l = 2
P = 0.9999231959668202 for n =4, l = 3というわけで最初に何の話をしていたか思い出しますと、再帰的プログラミングから始めてその代替手段としてのメモ化とループ、さらに物理学に出てくる特殊関数への応用について書いてきました。面白いと感じられましたらハートマークを押していただけると嬉しいです。
追記:
直交多項式以外の特殊関数として代表的な存在であるベッセル関数について書きました。
