円錐振り子の張力を求める問題で、あえて重力の方を分解して解いてみた

せっかく物理を学んでいるんだから何かアウトプットしたいなーと日頃思っていたのですが、なんせ大抵の物理の問題は誰かが解いていて、すでにテキストなりWEBなりのどこかしらに情報がアップされているだろうから、あえて同じものをアウトプットするのもやる気がでないなあと思っていたところ、ちょうどこんなアホみたいなこと誰も解説したりしてないだろというネタを見つけたので解説します。

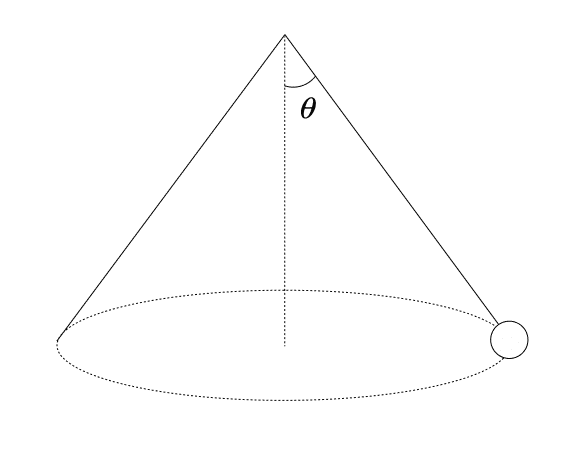
物理の円錐振り子の問題は上の図のようなもので、天井から長さ$${l}$$の糸で質量$${m}$$の質点を吊るしたところ、糸は鉛直線から角度$${\theta}$$を保って、質点は平面上を等速円運動した。という状況で、糸の張力$${T}$$を求めよという問題。

張力を分解する解法

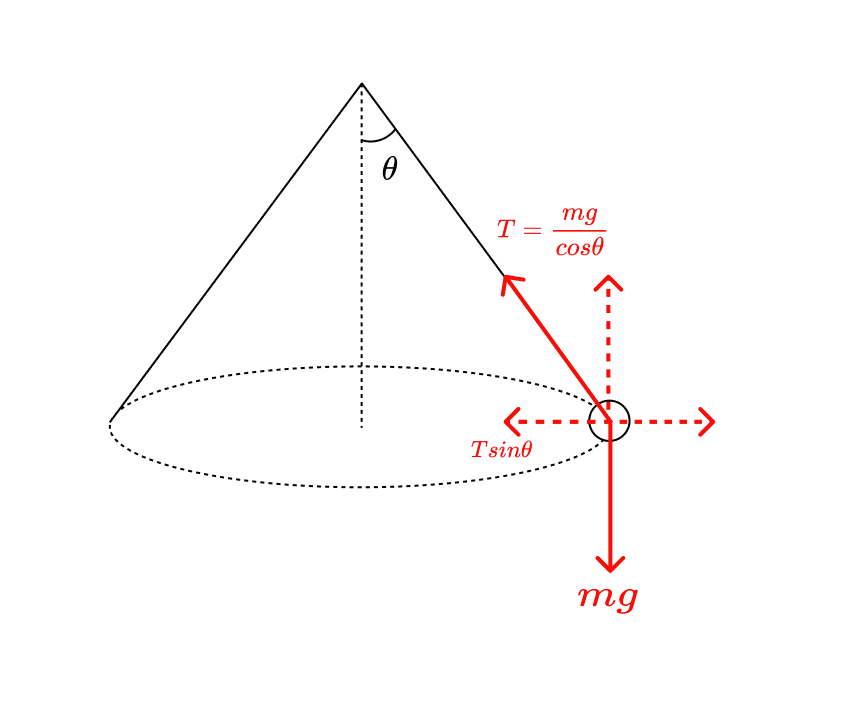
で、普通の解き方は上の図のように

1. それぞれに働いている力、張力$${T}$$と重力$${mg}$$を書き込む

2. 張力$${T}$$を鉛直方向と水平方向の力に分解する
   水平方向の力: $${Tsin\theta}$$
   鉛直方向の力は重力と釣り合っていなければならないので $${mg}$$

3. 三角比の関係から$${T=\frac{mg}{cos\theta}}$$となることが分かる

重力を分解する解法

だが、上の図のように、重力の方を張力に平行な方向の力と、それに垂直な力に分解したくなる人はぼく以外にもいるだろう（たぶん物理でよくある角度$${\theta}$$の坂を下る物体の問題のせい）。

しかしこれはうまくいかない。この形で力を分けてしまうと、上の図の$${mgsin\theta}$$と釣り合う力がないから。これを解決するには、質点の水平方向、遠心力$${f}$$をこの$${mgsin\theta}$$に対応する方向に分解してあげれば良い（青字）。これが、それぞれ$${fcos\theta}$$、$${fsin\theta}$$となる。$${f}$$は未知数だが、後ほど消せるので問題ない。

これで全ての力が釣り合いがとれる状態に出来たので、張力$${T}$$を求めていく。

$$
\begin{aligned}
fcos\theta=mgsin\theta\\
f=mgtan\theta\\
\end{aligned}
$$

$$
\begin{aligned}
T&=mgcos\theta+fsin\theta\\
&=mgcos\theta+mgtan\theta sin\theta\\
&=mg(cos\theta+\frac{sin^2\theta}{cos\theta})\\
&=mg(\frac{cos^2\theta+sin^2\theta}{cos\theta})\\
&=\frac{mg}{cos\theta}
\end{aligned}
$$

という形で、めでたく1つ目の解法と一致する張力$${T=\frac{mg}{cos\theta}}$$が得られた。

実際この解き方にメリットは全くなく、ただ計算がめんどくさいだけで、やる必要も覚える必要もないんだけど、理論的に1つ目の解法と一致する結果が出ないとおかしいと思ったので確かめずにはいられなかった。ちゃんと一致した結果が得られてスッキリ。