
「確率変数」とはなにかをわかりやすく
前回、大数の法則の記事を分かりやすく説明しようという記事を書きました。
そして、その記事の続きとしてもう少し数学的な内容に踏み込んだ大数の法則を解説したいと思ったのですが――
そのまえにこの大切なテーマに関して説明しておかないと、とてもじゃないけど数学的に正確な議論はできないと感じ、この記事は別に独立させることにしました。
ということで、今回のテーマは確率変数です。
確率変数とは
わかりそうでわからないこの言葉。
高校生のときには「ある試行に対してその値をとる確率が定まる変数を確率変数という」と定義されていました。
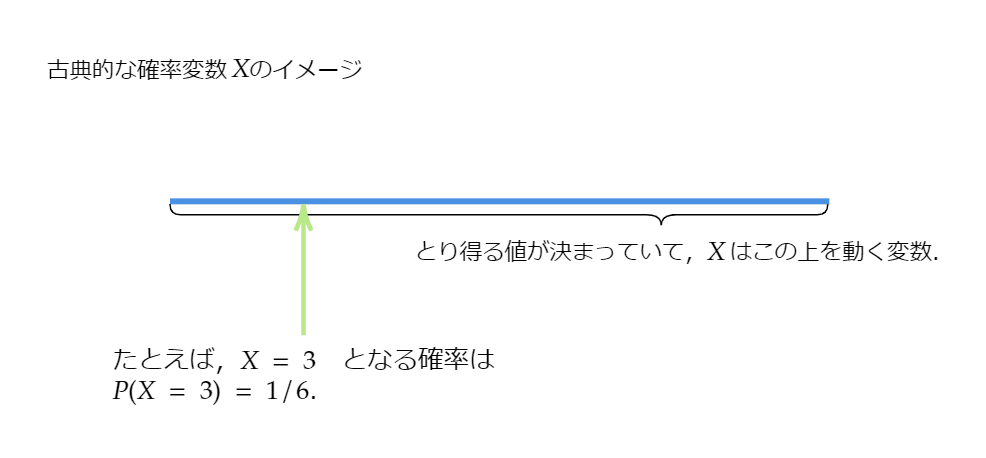
でもこの文章、いまいちピンとこないんですよね。
その値をとる確率が定まる、っていうけど、じゃあ確率ってなんなの? とか。
その値をとるっていうけどどういう風にとるの? とか。これに対し、古典的にはランダムに値をとると答えざるを得なかったんですが、このランダムという概念は実はとっても難しいんです。
実は今でも、ランダムとはなにかは数学的に定式化できていません。
とにかく、確率変数という言葉はあいまいで突っ込みどころ満載だったわけです。(すこし悪く言い過ぎたかもしれませんが、古典確率論も応用上は大きな成果を上げていたんですけどね)
しかし、20世紀の偉大な数学者であるコルモゴロフが数学の2つの分野を融合させ、確率論に大きな進化をもたらしました。
それは、確率論と測度論の融合です。
測度論というのはすごく簡単に言うと、面積とはなにかを徹底的に考える分野です。
そして、コルモゴロフは「確率とは面積である」ととらえることによってさまざまな事実が美しく、そして数学的に正確に描かれることを見出しました。
そして、面積を図ることができる空間、測度空間上で確率変数を定義しました。
コルモゴロフの定義では、確率変数とは測度空間上の関数です。
ここ、注意してください。確率変数は名前こそ変数なのですが、その実態は関数であると考えているんです。
変数とは名ばかりなんですね。
どのようなイベントにどのような値が紐づいているのかを対応付ける関数として確率変数を定義しました。

そして、確率変数を測度空間(=面積を図ることができる空間)上の関数で定めたため、ランダムという概念に頼る必要がなくなりました。
関数なのですから、どこからどこへの対応関係なのかはっきり決まっていると思ってよいわけです。
「あるイベントが起こる確率は?」という質問にも明確に答えられます。
それは、そのイベントの面積だ、と言えるんです。

標本空間こそが面積を測れる空間のことです。標本空間Ωの横にあるやわらかいBみたいなのはイベントの集合です。その横のPは面積を測るための関数ですね。どちらも測度論を取り入れたことによって出てくるものです。
確率変数が関数であるということをより強く意識してもらうためには、次のような図で確率変数をイメージしてもらってもよいです。
そのときそのときでイメージしやすい方を考えるために使ってもらえればよいと思います。


このイメージを見てもらうとほんとにy=f(x)という関数と同じ形だということがわかってもらえると思います。
細かいことを言うと確率測度Pはその都度変わっています。というかこの確率測度を取り換えるということを理解すれば、もはや離散型の確率変数と連続型の確率変数は区別する必要はありません。
入っている測度が違うから、の一言でかたずけられるんです。
というわけで今回は確率変数の説明でした。
次回は大数の法則に戻りたいと思います。
<<前回
>>次回
