
[Python]医療費データを主成分分析してみた(続き)
こんにちは。機械学習勉強中のあおじるです。
前回の記事で、協会けんぽの過去10年間、47都道府県別の医療費データを主成分分析(PCA)しました。今回はその続きです。
1.全国平均を主成分座標平面上にプロット
2.主成分分析の結果を3次元プロット
してみます。
前回と同じく、Python、Google Colaboratoryを使用します。
1.全国平均を主成分座標平面上にプロット
前回は、47都道府県別のデータを主成分分析(PCA)し、結果を主成分の座標平面上にプロットしてみましたが、今回は、その同じ主成分の座標平面上に全国平均(47都道府県の加重平均)をプロットしてみます。
前回、年月別の都道府県別データと年度別の都道府県別データのそれぞれにPCAを実行しましたので、今回も年月別の全国平均(10年×12か月分)と年度別の全国平均(10年度分)をそれぞれプロットしてみます。
1.1.年月別
まず、年度別から。
前回の年月別都道府県別のデータを全国集計して、年月別の全国平均を計算します(単純平均ではなく加重平均を計算するため、3要素を計算する前のデータに戻って全国集計し、全国平均の3要素を計算します。)。
# 全国平均を計算
import pandas as pd
# 都道府県別データ
df_ymtsn_XC_k = pd.read_csv('./df_ymtsn_XC_k.csv', index_col=None)
print(df_ymtsn_XC_k.shape)
# (90240, 45)
# 全国集計
df_ymsn_XC_k = df_ymtsn_XC_k.iloc[:,[0]+list(range(2,15))].groupby(['ym', 's', 'n'], as_index=False).sum()
print(df_ymsn_XC_k.shape)
# (1920, 14)
print(df_ymsn_XC_k.columns)
# Index(['ym', 's', 'n', 'P', 'Ken_1', 'Ken_2', 'Ken_3', 'Nit_1', 'Nit_2',
# 'Nit_3', 'Ten_1', 'Ten_2', 'Ten_3', 'Ten_4'],
# dtype='object')
# 3要素の計算
df_ymsn_XC_k['KperP_1'] = df_ymsn_XC_k['Ken_1'] / df_ymsn_XC_k['P']
df_ymsn_XC_k['KperP_2'] = df_ymsn_XC_k['Ken_2'] / df_ymsn_XC_k['P']
df_ymsn_XC_k['KperP_3'] = df_ymsn_XC_k['Ken_3'] / df_ymsn_XC_k['P']
df_ymsn_XC_k['NperK_1'] = df_ymsn_XC_k['Nit_1'] / df_ymsn_XC_k['Ken_1']
df_ymsn_XC_k['NperK_2'] = df_ymsn_XC_k['Nit_2'] / df_ymsn_XC_k['Ken_2']
df_ymsn_XC_k['NperK_3'] = df_ymsn_XC_k['Nit_3'] / df_ymsn_XC_k['Ken_3']
df_ymsn_XC_k['TperN_1'] = df_ymsn_XC_k['Ten_1'] / df_ymsn_XC_k['Nit_1']
df_ymsn_XC_k['TperN_2'] = df_ymsn_XC_k['Ten_2'] / df_ymsn_XC_k['Nit_2']
df_ymsn_XC_k['TperN_3'] = df_ymsn_XC_k['Ten_3'] / df_ymsn_XC_k['Nit_3']
df_ymsn_XC_k['TperN_4'] = df_ymsn_XC_k['Ten_4'] / df_ymsn_XC_k['Nit_2']
print(df_ymsn_XC_k.shape)
# (1920, 24)
print(df_ymsn_XC_k.columns)
# Index(['ym', 's', 'n', 'P', 'Ken_1', 'Ken_2', 'Ken_3', 'Nit_1', 'Nit_2',
# 'Nit_3', 'Ten_1', 'Ten_2', 'Ten_3', 'Ten_4', 'KperP_1', 'KperP_2',
# 'KperP_3', 'NperK_1', 'NperK_2', 'NperK_3', 'TperN_1', 'TperN_2',
# 'TperN_3', 'TperN_4'],
# dtype='object')
col_names = ['ym','s','n']
var_names = []
for x in ['KperP','NperK','TperN']:
if x != 'TperN':
for k in [1,2,3]:
var_names.append(x+'_'+str(k))
else:
for k in [1,2,3,4]:
var_names.append(x+'_'+str(k))
col_names = col_names + var_names
df_ymsn_C10 = df_ymsn_XC_k.copy()
df_ymsn_C10 = df_ymsn_C10[col_names]
df_ymsn_C10
print(df_ymsn_C10.shape)
# (1920, 13)
print(df_ymsn_C10.columns)
# Index(['ym', 's', 'n', 'KperP_1', 'KperP_2', 'KperP_3', 'NperK_1', 'NperK_2',
# 'NperK_3', 'TperN_1', 'TperN_2', 'TperN_3', 'TperN_4'],
# dtype='object')
# データのpivot
df_ym_C10_sn = df_ymsn_C10.pivot(index=['ym'], columns=['s','n'], values=var_names)
col_names = []
for ck in var_names:
for s in [1,2]:
for n in [1,2,3,4,5,6,7,8]:
col_names.append(ck+'_'+str(s)+'_'+str(n))
df_ym_C10_sn = df_ym_C10_sn.set_axis(col_names, axis='columns')
df_ym_C10_sn = df_ym_C10_sn.reset_index()
print(df_ym_C10_sn.shape)
# (120, 161)
print(df_ym_C10_sn.columns)
# Index(['ym', 'KperP_1_1_1', 'KperP_1_1_2', 'KperP_1_1_3', 'KperP_1_1_4',
# 'KperP_1_1_5', 'KperP_1_1_6', 'KperP_1_1_7', 'KperP_1_1_8',
# 'KperP_1_2_1',
# ...
# 'TperN_4_1_7', 'TperN_4_1_8', 'TperN_4_2_1', 'TperN_4_2_2',
# 'TperN_4_2_3', 'TperN_4_2_4', 'TperN_4_2_5', 'TperN_4_2_6',
# 'TperN_4_2_7', 'TperN_4_2_8'],
# dtype='object', length=161)
df_ymsn_XC..
df_ymsn_C10.to_csv('./df_ymsn_C10.csv', index=None)
df_ym_C10_sn.to_csv('./df_ym_C10_sn.csv',index=None)これで、10年×12か月=120時点における160項目の全国平均のデータができました。
ここから数値部分のみ取り出して、主成分へ変換します。
前回は前処理としてMinMaxスケーリングした後にPCAを実行しましたので、そのときの変換(スケーリング+PCA)をscaler_ymとpca_ymとして保存しておき、それを全国平均のデータに適用します。
# 前回の変換
df_ym = pd.read_csv('./df_ymt_C10_sn.csv')
# データ
X = df_ym.iloc[:,2:] # 数値部分のみ
print(X.shape) # (5640, 160)
# スケーリング
from sklearn import preprocessing
scaler_ym = preprocessing.MinMaxScaler()
X = scaler_ym.fit_transform(X)
print(X.shape) # (5640, 160)
# PCA
from sklearn.decomposition import PCA
pca_ym = PCA(n_components=160)
PC_ym = pca_ym.fit_transform(X)
print(PC_ym.shape) # (5640, 160)このスケーリング(scaler_ym)とPCA(pca_ym)の変換を全国平均のデータ(120時点×160項目)に適用します。
# 全国平均のデータ
df_zenkoku = df_ym_C10_sn.copy()
X_zenkoku = df_zenkoku.iloc[:,1:] # 数値部分のみ
print(X_zenkoku.shape) # (120, 160)
# 上と同じスケーリングの変換を適用
X_zenkoku = scaler_ym.transform(X_zenkoku)
print(X_zenkoku.shape) # (120, 160)
# 上と同じPCAの変換を適用
PC_ym_zenkoku = pca_ym.transform(X_zenkoku)
print(PC_ym_zenkoku.shape) # (120, 160)結果を前回のプロットに重ねて描きます。色分けは前回と同じで、左側が年月別の色分け、右側が都道府県別の色分けです。前回の都道府県別のプロットを薄く小さく、今回の全国平均のプロットを濃く大きくしてあります。
# プロット
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import preprocessing
le = preprocessing.LabelEncoder()
# 都道府県別データ_年月ym
le.fit(df_ym['ym'])
label_ym = le.transform(df_ym['ym'])
cp = sns.color_palette("hls", n_colors=10*12+1)
color_ym = [cp[x] for x in label_ym]
# 都道府県別データ_都道府県t
le.fit(df_ym['t'])
label_t = le.transform(df_ym['t'])
cp = sns.color_palette("hls", n_colors=47+1)
color_t = [cp[x] for x in label_t]
# 全国平均データ_年月ym
le.fit(df_zenkoku['ym'])
label_ym_zenkoku = le.transform(df_zenkoku['ym'])
cp_zenkoku = sns.color_palette("hls", n_colors=10*12+1)
color_ym_zenkoku = [cp_zenkoku[x] for x in label_ym_zenkoku]
n = 10
for i in range(n-1):
for j in range(i+1,n):
if (i==0 or j==i+1):
print('PC{} x PC{}'.format(i+1, j+1))
plt.figure(figsize=(12,5))
plt.subplot(1, 2, 1)
plt.title('PC{} x PC{} colored by ym'.format(i+1, j+1))
plt.xlabel('PC{}'.format(i+1))
plt.ylabel('PC{}'.format(j+1))
plt.scatter(x=PC_ym[:,i], y=PC_ym[:,j], c=color_ym, s=10, alpha=0.1)
plt.scatter(x=PC_ym_zenkoku[:,i], y=PC_ym_zenkoku[:,j], c=color_ym_zenkoku)
plt.subplot(1, 2, 2)
plt.title('PC{} x PC{} colored by t'.format(i+1, j+1))
plt.xlabel('PC{}'.format(i+1))
plt.ylabel('PC{}'.format(j+1))
plt.scatter(x=PC_ym[:,i], y=PC_ym[:,j], c=color_t, s=10, alpha=0.1)
plt.scatter(x=PC_ym_zenkoku[:,i], y=PC_ym_zenkoku[:,j], c='black')
plt.show()
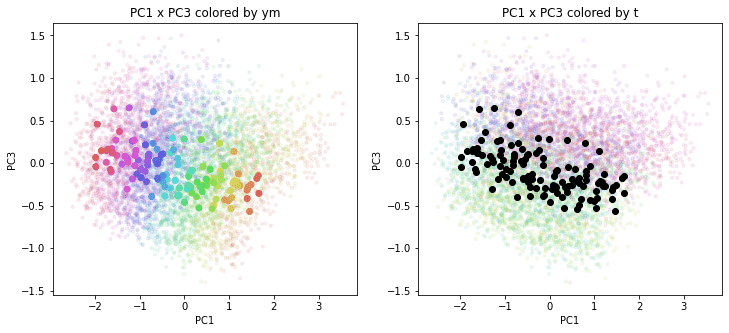


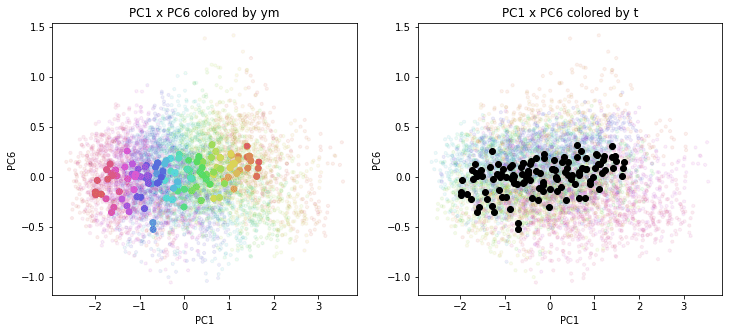







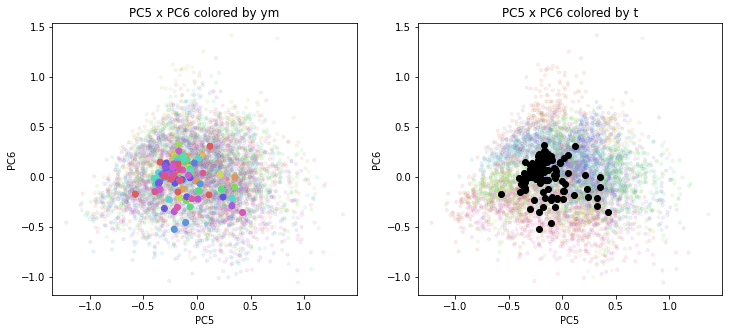




PC1×PCn(n>1)を見ると、全国平均は(多少上下(PCn方向)に変動しながらも)概ね時間の経過とともにPC1軸に沿って動いているのがわかります。PCn×PCm(n,m>1)を見ると、全国平均はほぼ中央付近に固まって分布しています。やはり、PC1が時間の経過を表す成分で、PC2以降が地域性を表す成分のようです。
1.2.年度別
年月別と同様のことを年度別の全国平均についても行います。
まず、年度別の全国平均を計算します。
# 全国平均を計算
import pandas as pd
# 都道府県別データ
df_ytsn_XC_k = pd.read_csv('./df_ytsn_XC_k.csv', index_col=None)
print(df_ytsn_XC_k.shape)
# (7520, 36)
# 全国集計
df_ysn_XC_k = df_ytsn_XC_k.iloc[:,[0]+list(range(2,18))].groupby(['y','s','n'], as_index=False).sum()
print(df_ysn_XC_k.shape)
# (160, 17)
print(df_ysn_XC_k.columns)
# Index(['y', 's', 'n', 'P', 'Ken_1', 'Ken_2', 'Ken_3', 'Nit_1', 'Nit_2',
# 'Nit_3', 'Ten_1', 'Ten_2', 'Ten_3', 'Ten_4', 'KperP_1', 'KperP_2',
# 'KperP_3'],
# dtype='object')
# 医療費の3要素の計算
df_ysn_XC_k['KperP_1'] = df_ysn_XC_k['Ken_1'] /(df_ysn_XC_k['P']/12)
df_ysn_XC_k['KperP_2'] = df_ysn_XC_k['Ken_2'] /(df_ysn_XC_k['P']/12)
df_ysn_XC_k['KperP_3'] = df_ysn_XC_k['Ken_3'] /(df_ysn_XC_k['P']/12)
df_ysn_XC_k['NperK_1'] = df_ysn_XC_k['Nit_1'] / df_ysn_XC_k['Ken_1']
df_ysn_XC_k['NperK_2'] = df_ysn_XC_k['Nit_2'] / df_ysn_XC_k['Ken_2']
df_ysn_XC_k['NperK_3'] = df_ysn_XC_k['Nit_3'] / df_ysn_XC_k['Ken_3']
df_ysn_XC_k['TperN_1'] = df_ysn_XC_k['Ten_1'] / df_ysn_XC_k['Nit_1']
df_ysn_XC_k['TperN_2'] = df_ysn_XC_k['Ten_2'] / df_ysn_XC_k['Nit_2']
df_ysn_XC_k['TperN_3'] = df_ysn_XC_k['Ten_3'] / df_ysn_XC_k['Nit_3']
df_ysn_XC_k['TperN_4'] = df_ysn_XC_k['Ten_4'] / df_ysn_XC_k['Nit_2']
print(df_ysn_XC_k.shape)
# (160, 24)
print(df_ysn_XC_k.columns)
# Index(['y', 's', 'n', 'P', 'Ken_1', 'Ken_2', 'Ken_3', 'Nit_1', 'Nit_2',
# 'Nit_3', 'Ten_1', 'Ten_2', 'Ten_3', 'Ten_4', 'KperP_1', 'KperP_2',
# 'KperP_3', 'NperK_1', 'NperK_2', 'NperK_3', 'TperN_1', 'TperN_2',
# 'TperN_3', 'TperN_4'],
# dtype='object')
col_names = ['y','s','n']
var_names = []
for x in ['KperP','NperK','TperN']:
if x != 'TperN':
for k in [1,2,3]:
var_names.append(x+'_'+str(k))
else:
for k in [1,2,3,4]:
var_names.append(x+'_'+str(k))
col_names = col_names + var_names
df_ysn_C10 = df_ysn_XC_k.copy()
df_ysn_C10 = df_ysn_C10[col_names]
df_ysn_C10
print(df_ysn_C10.shape)
# (160, 13)
print(df_ysn_C10.columns)
# Index(['y', 's', 'n', 'KperP_1', 'KperP_2', 'KperP_3', 'NperK_1', 'NperK_2',
# 'NperK_3', 'TperN_1', 'TperN_2', 'TperN_3', 'TperN_4'],
# dtype='object')
# データのpivot
df_y_C10_sn = df_ysn_C10.pivot(index=['y'], columns=['s','n'], values=var_names)
col_names = []
for ck in var_names:
for s in [1,2]:
for n in [1,2,3,4,5,6,7,8]:
col_names.append(ck+'_'+str(s)+'_'+str(n))
df_y_C10_sn = df_y_C10_sn.set_axis(col_names, axis='columns')
df_y_C10_sn = df_y_C10_sn.reset_index()
print(df_y_C10_sn.shape)
# (10, 161)
print(df_y_C10_sn.columns)
# Index(['y', 'KperP_1_1_1', 'KperP_1_1_2', 'KperP_1_1_3', 'KperP_1_1_4',
# 'KperP_1_1_5', 'KperP_1_1_6', 'KperP_1_1_7', 'KperP_1_1_8',
# 'KperP_1_2_1',
# ...
# 'TperN_4_1_7', 'TperN_4_1_8', 'TperN_4_2_1', 'TperN_4_2_2',
# 'TperN_4_2_3', 'TperN_4_2_4', 'TperN_4_2_5', 'TperN_4_2_6',
# 'TperN_4_2_7', 'TperN_4_2_8'],
# dtype='object', length=161)
df_ysn_XC_k.to_csv('./df_ysn_XC_k.csv', index=None)
df_ysn_C10.to_csv('./df_ysn_C10.csv', index=None)
df_y_C10_sn.to_csv('./df_y_C10_sn.csv',index=None)これで、10年度分の160項目の全国平均のデータができました。
ここから数値部分のみ取り出して、主成分へ変換します。
前回のスケーリングの変換scaler_yとPCAの変換pca_yを保存しておきます。
# 前回の変換
df_y = pd.read_csv('./df_yt_C10_sn.csv')
# データ
X = df_y.iloc[:,2:] # 数値部分のみ
print(X.shape) # (470, 160)
# スケーリング
from sklearn import preprocessing
scaler_y = preprocessing.MinMaxScaler()
X = scaler_y.fit_transform(X)
print(X.shape) # (470, 160)
# PCA
from sklearn.decomposition import PCA
pca_y = PCA(n_components=160)
PC_y = pca_y.fit_transform(X)
print(PC_y.shape) # (470, 160)全国平均のデータから数値部分のみ取り出して、スケーリングの変換scaler_yとPCAの変換pca_yを適用して、主成分へ変換します。
# 全国平均のデータ
df_y_zenkoku = df_y_C10_sn.copy()
X_zenkoku = df_y_zenkoku.iloc[:,1:] # 数値部分のみ
print(X_zenkoku.shape) # (10, 160)
# 上のスケーリングと同じ変換
X_zenkoku = scaler_y.transform(X_zenkoku)
print(X_zenkoku.shape) # (10, 160)
# 上のPCAと同じ変換
PC_y_zenkoku = pca_y.transform(X_zenkoku)
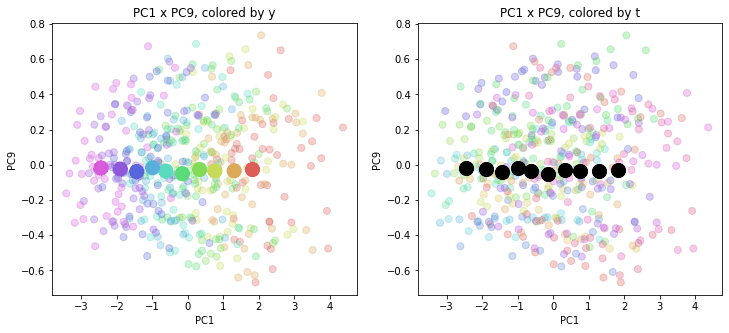
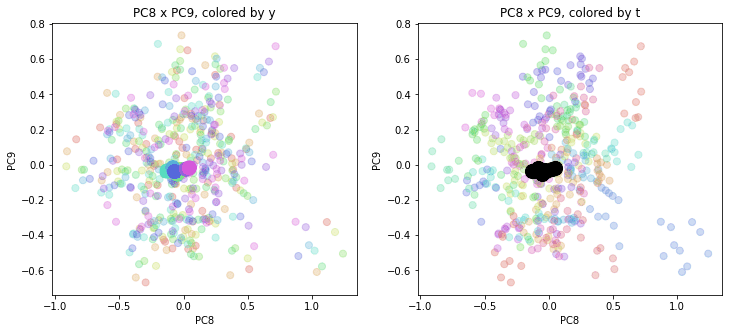
print(PC_y_zenkoku.shape) # (10, 160)結果を前回のプロットに重ねて描きます。色分けは前回と同じで、左側が年度別の色分け、右側が都道府県別の色分けです。
# プロット
from sklearn import preprocessing
le = preprocessing.LabelEncoder()
# 都道府県別データ_年度y
le.fit(df_y['y'])
label_y = le.transform(df_y['y'])
cp = sns.color_palette("hls", n_colors=10+1)
color_y = [cp[x] for x in label_y]
# 都道府県別データ_都道府県t
le.fit(df_y['t'])
label_t = le.transform(df_y['t'])
cp = sns.color_palette("hls", n_colors=47+1)
color_t = [cp[x] for x in label_t]
# 全国平均データ_年月y
le.fit(df_y_zenkoku['y'])
label_y_zenkoku = le.transform(df_y_zenkoku['y'])
cp_zenkoku = sns.color_palette("hls", n_colors=10+1)
color_y_zenkoku = [cp_zenkoku[x] for x in label_y_zenkoku]
n = 10
for i in range(n-1):
for j in range(i+1,n):
if (i==0 or j==i+1):
print('PC{} x PC{}'.format(i+1, j+1))
plt.figure(figsize=(12,5))
plt.subplot(1, 2, 1)
plt.title('PC{} x PC{}, colored by y'.format(i+1, j+1))
plt.xlabel('PC{}'.format(i+1))
plt.ylabel('PC{}'.format(j+1))
plt.scatter(x=PC_y[:,i], y=PC_y[:,j], c=color_y, s=50, alpha=0.3)
plt.scatter(x=PC_y_zenkoku[:,i], y=PC_y_zenkoku[:,j], s=200, c=color_y_zenkoku)
plt.subplot(1, 2, 2)
plt.title('PC{} x PC{}, colored by t'.format(i+1, j+1))
plt.xlabel('PC{}'.format(i+1))
plt.ylabel('PC{}'.format(j+1))
plt.scatter(x=PC_y[:,i], y=PC_y[:,j], c=color_t, s=50, alpha=0.3)
plt.scatter(x=PC_y_zenkoku[:,i], y=PC_y_zenkoku[:,j], s=200, c='black')
plt.show()














2.主成分分析の結果を3次元プロット
PCAの結果を2次元にプロットしてきましたが、3次元にもプロットしてみます。(年度別のデータについて行います。)
3次元プロットはmatplotlibのチュートリアルを参考にしました。
# 3次元プロット
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
n = 10
for i in range(n):
for j in range(i+1,n):
for k in range(j+1,n):
if i==0 or j==i+1 or k==j+1:
print('PC{} x PC{} x PC{}'.format(i+1,j+1,k+1))
fig = plt.figure(figsize=(15, 6))
ax = fig.add_subplot(1, 2, 1, projection='3d')
ax.scatter(PC_y[:,i], PC_y[:,j], PC_y[:,k], c=color_y, s=30)
ax.scatter(PC_y_zenkoku[:,i], PC_y_zenkoku[:,j], PC_y_zenkoku[:,k],
c='black', s=80)
ax.set_title('PC{} x PC{} x PC{}, colored by y'.format(i+1,j+1,k+1))
ax.set_xlabel('PC{}'.format(i+1))
ax.set_ylabel('PC{}'.format(j+1))
ax.set_zlabel('PC{}'.format(k+1))
# ax.w_xaxis.set_ticklabels([])
# ax.w_yaxis.set_ticklabels([])
# ax.w_zaxis.set_ticklabels([])
ax = fig.add_subplot(1, 2, 2, projection='3d')
ax.scatter(PC_y[:,i], PC_y[:,j], PC_y[:,k], c=color_t, s=30)
ax.scatter(PC_y_zenkoku[:,i], PC_y_zenkoku[:,j], PC_y_zenkoku[:,k],
c='black', s=80)
ax.set_title('PC{} x PC{} x PC{}, colored by t'.format(i+1,j+1,k+1))
ax.set_xlabel('PC{}'.format(i+1))
ax.set_ylabel('PC{}'.format(j+1))
ax.set_zlabel('PC{}'.format(k+1))
# ax.w_xaxis.set_ticklabels([])
# ax.w_yaxis.set_ticklabels([])
# ax.w_zaxis.set_ticklabels([])
plt.show()



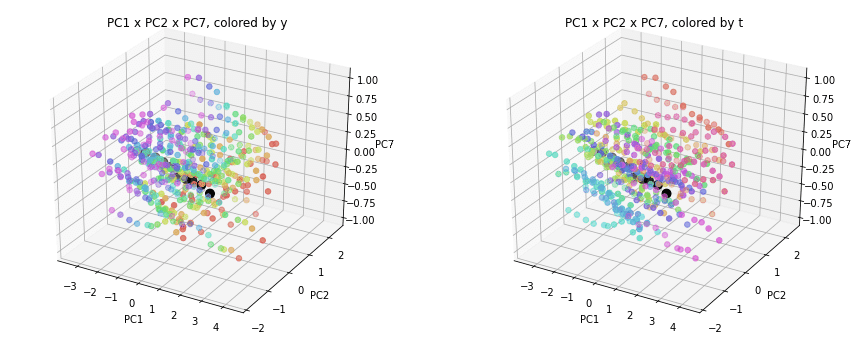











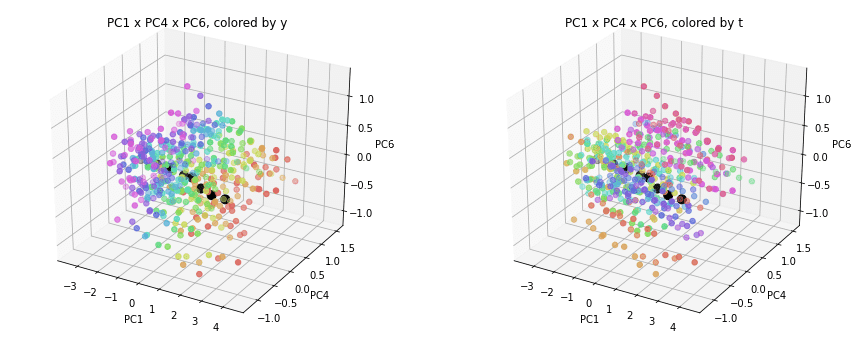





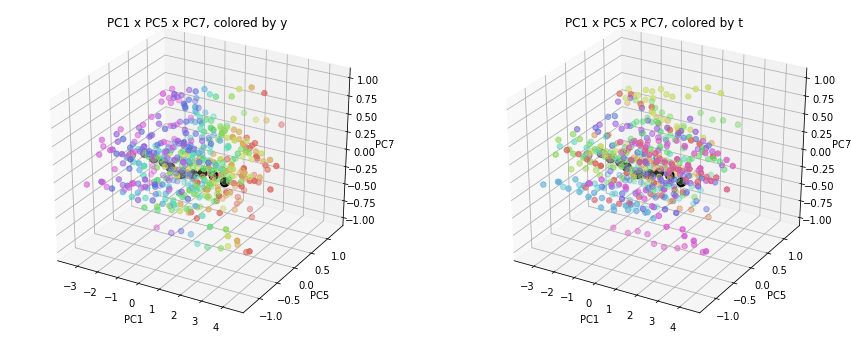












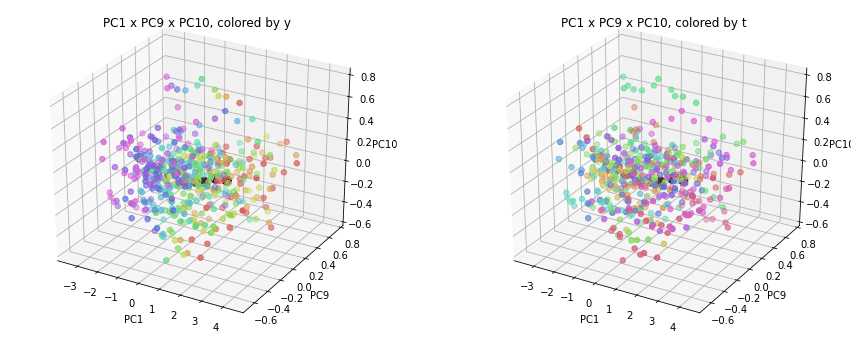












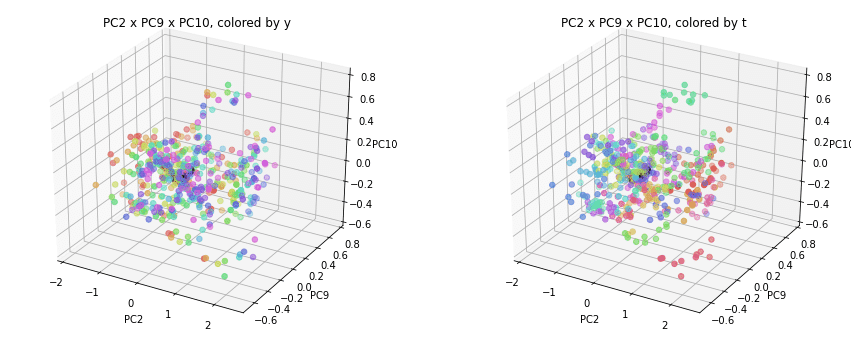



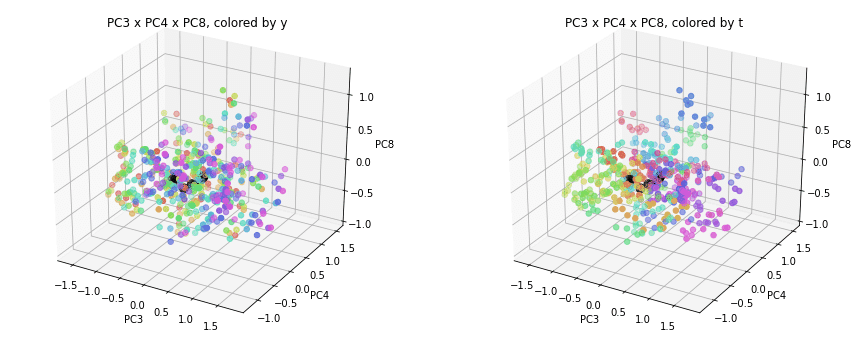






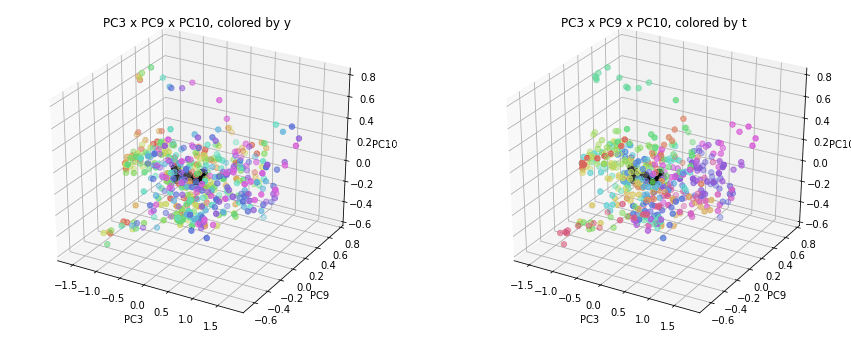












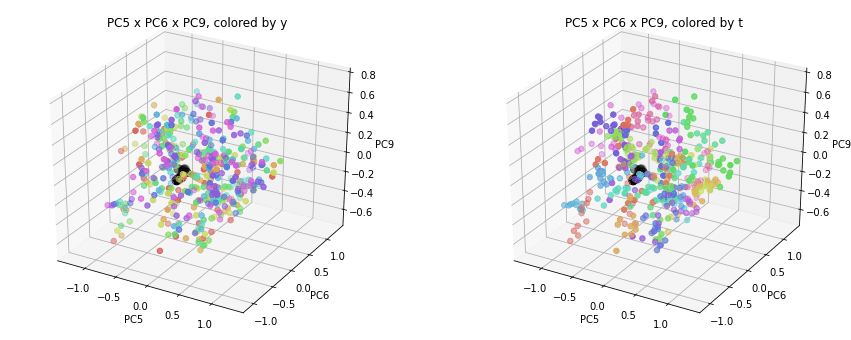













PC1×PCn×PCm(n,m>1)を見ると、全国平均(黒の点)を囲んで都道府県(カラーの点)が概ね相対的な位置関係を保ったままPC1方向に平行移動しています。
PC2×PC3×PC4以降を見ると、全国平均は中央付近に固まり、都道府県はその周りに都道府県ごと(色ごと)に固まって分布しています。2次元プロットでは重なっていた色同士が、3次元プロットではもう少しきれいに分離できているようです。
おわりに
今回は、前回の都道府県別医療費3要素データの主成分分析の結果をプロットしたのと同じ主成分座標平面上に、全国平均をプロットしてみました。
また、主成分分析の結果を3次元にプロットすることで、前回の2次元プロットでは重なっていたところを分離することができました。
最後まで読んでいただき、ありがとうございました。
自分でもだんだん何をやっているのかわからなくなってきましたが、お気づきの点等ありましたら、コメントいただけますと幸いです。
#医療費 , #医療費の3要素 , #医療費の地域差 , #地域差 , #地域間格差 , #協会けんぽ , #主成分分析 , #PCA
