
[Python]健診データを次元削減してみた:PCAとUMAPによる次元削減
はじめに
こんにちは、機械学習勉強中のあおじるです。
これまで、全国健康保険協会(協会けんぽ)の医療費データを使っていくつか記事を書きました。
今回は、別のデータとして健診のデータを使ってみました。
データの取得
全国健康保険協会(協会けんぽ)のホームページから健診データを取得します。
場所は、「統計情報」の「医療費分析」というページの中に年度ごとのデータがあります(年度によって資料の様式が違っていて探しにくいですが。)。
令和元年度~平成29年度(2019~2017年度)
「1.都道府県医療費の状況」という資料のバックデータのエクセルファイルの中に年度ごとの集計があります。https://www.kyoukaikenpo.or.jp/g7/cat740/sb7210/sbb7211/bunseki1/平成28年度~平成23年度(2016~2011年度)
「3.都道府県医療費等の基礎データ」という資料のエクセルファイルの中に年度ごとの集計があります。https://www.kyoukaikenpo.or.jp/g7/cat740/sb7210/sbb7214/bunseki4/
データは、都道府県支部ごとに、男女別(男女計・男性・女性別)に
・メタボリックリスク保有率
・メタボリックリスク予備群の割合
・腹囲のリスク保有率
・血圧のリスク保有率
・脂質のリスク保有率
・代謝のリスク保有率
・喫煙者の割合
・BMIのリスク保有率
・中性脂肪のリスク保有率
・HDLコレステロールのリスク保有率
があります。各指標の定義は次のようになっています。
集計対象データは(中略)年度末に35歳以上75歳以下に達し、1年間継続して協会けんぽに加入した被保険者が年度中に受診した生活習慣病予防健診(一般健診、付加健診)データのうち、特定保健指導レベルが判定不可能でないもの(35~39歳の特定保健指導レベルは40歳以上の階層化の方法に準じて判定)とし、リスク保有者割合等の分母は、特に断りのない場合、当該リスクの判定が可能なデータの総数としている。
① メタボリックリスク保有率は、③かつ④~⑥のうち2項目以上に該当する者の割合(分母は集計対象データ総数)
② メタボリックリスク予備群の割合は、③かつ④~⑥のうち1項目に該当する者の割合(分母は集計対象データ総数)
③ 腹囲のリスク保有率は、内臓脂肪面積が100㎠以上の者(ただし内臓脂肪面積の検査値がない場合は、腹囲が男性で85cm以上、女性で90cm以上の者)の割合
④ 血圧のリスク保有率は、収縮期血圧130mmHg以上、または拡張期血圧85mmHg以上、または高血圧に対する薬剤治療ありの者の割合
⑤ 脂質のリスク保有率は、中性脂肪150mg/dl以上、またはHDLコレステロール40mg/dl未満、または脂質異常症に対する薬剤治療ありの者の割合
⑥ 代謝のリスク保有率は、空腹時血糖110mg/dl以上(ただし空腹時血糖の検査がない場合は、HbA1c 6.0%以上)、または糖尿病に対する薬剤治療ありの者の割合
⑦ 喫煙者の割合は問診票において喫煙者であると回答した者の割合
⑧ BMIのリスク保有率はBMI(肥満度)が25以上の者の割合
⑨ 脂質(中性脂肪)のリスク保有率は中性脂肪150mg/dl以上の者の割合
⑩ 脂質(HDLコレステロール)のリスク保有率はHDLコレステロール40mg/dl未満の者の割合
ただし、平成28~26年度の3年間分は「メタボリックリスク予備群の割合」が抜けているようです。
以下では、途中の年度に抜けのある「メタボリックリスク予備群の割合」を除く9個の指標を使います。
データの加工
エクセルファイルのデータを読み込んで、次の形に整理したものを使います。
年度、性、都道府県別の9指標
$$
\def\arraystretch{1.5}
\begin{array}{c:c:c|c:c:c:c:c:c:c}
\textsf{y} & \textsf{s} & \textsf{t} & \textsf{metabo} & \textsf{hukui} & \textsf{ketsuatsu} & \textsf{sisitsu} & \textsf{taisha} & \cdots & \textsf{hdl} \\ \hline
2011 & 1 & 1 & {} & {} & {} & {} & {} & {} & {} \\
2011 & 1 & 2 & {} & {} & {} & {} & {} & {} & {} \\
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\
2011 & 1 & 47 & {} & {} & {} & {} & {} & {} & {} \\
2011 & 2 & 1 & {} & {} & {} & {} & {} & {} & {} \\
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\
2019 & 2 & 47 & {} & {} & {} & {} & {} & {} & {}
\end{array}
$$
・年度(y)は、2011~2019の9年度
・性(s)は、1:男性、2:女性の2区分(「男女計」は除く。)
・都道府県(t)は、1:北海道、・・・、47:沖縄の47区分(「全国平均」は除く。)
で、9×2×47=846行、
指標は、
・metabo:① メタボリックリスク保有率
・hukui:③ 腹囲のリスク保有率
・ketsuatsu:④ 血圧のリスク保有率
・sisitsu:⑤ 脂質のリスク保有率
・taisha:⑥ 代謝のリスク保有率
・kitsuen:⑦ 喫煙者の割合
・bmi:⑧ BMIのリスク保有率
・chuseisibo:⑨ 脂質(中性脂肪)のリスク保有率
・hdl:⑩ 脂質(HDLコレステロール)のリスク保有率
の9指標のデータフレームになります。
import pandas as pd
df_yst_Kensin = pd.read_excel('./Data/健診結果.xlsx')
print(df_yst_Kensin.shape)
# (846, 12)
# 846=9*2*47
print(df_yst_Kensin.columns)
# Index(['y', 's', 't', 'metabo', 'hukui', 'ketsuatsu', 'sisitsu', 'taisha',
# 'kitsuen', 'bmi', 'chuseisibo', 'hdl'],
# dtype='object')性別を列方向に移して、年度×都道府県ごとのデータに変形します。
var_names = list(df_yst_Kensin .columns)[3:]
print(var_names)
# ['metabo', 'hukui', 'ketsuatsu', 'sisitsu', 'taisha', 'kitsuen', 'bmi', 'chuseisibo', 'hdl']
df_yt_Kensin_s = df_yst_Kensin.pivot(index=['y','t'], columns=['s'], values=var_names)
print(df_yt_Kensin_s.shape)
# (423, 18)
# 423=9*47
col_names = []
for v in var_names:
for s in [1,2]:
col_names.append(v+'_'+str(s))
df_yt_Kensin_s = df_yt_Kensin_s.set_axis(col_names, axis='columns')
df_yt_Kensin_s = df_yt_Kensin_s.reset_index()
print(df_yt_Kensin_s.shape)
# (423, 20)
print(df_yt_Kensin_s.columns)
# Index(['y', 't', 'metabo_1', 'metabo_2', 'metabo_3', 'hukui_1', 'hukui_2',
# 'hukui_3', 'ketsuatsu_1', 'ketsuatsu_2', 'ketsuatsu_3', 'sisitsu_1',
# 'sisitsu_2', 'sisitsu_3', 'taisha_1', 'taisha_2', 'taisha_3',
# 'kitsuen_1', 'kitsuen_2', 'kitsuen_3', 'bmi_1', 'bmi_2', 'bmi_3',
# 'chuseisibo_1', 'chuseisibo_2', 'chuseisibo_3', 'hdl_1', 'hdl_2',
# 'hdl_3'],
# dtype='object')
print(df_yt_Kensin_s)
df_yt_Kensin_s.to_csv('./Data/df_yt_Kensin_s.csv', index=None)これで、423行(9年度×47都道府県)×18列(9指標×2性別)のデータができました。
次元削減
医療費データの次元削減の記事と同様に、PCAとUMAPで次元削減します。
# 数値部分のみ取り出し
df = df_yt_Kensin_s.copy()
X = df.iloc[:,2:]
print(X.shape)
# (423, 18)
# 423=9*47
# スケーリング
from sklearn import preprocessing
scaler = preprocessing.MinMaxScaler()
X = scaler.fit_transform(X)
print(X.shape)
# (423, 18)結果は、以前の記事と同じ色分けをします。
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import preprocessing
le = preprocessing.LabelEncoder()
# 年度y
label_y = le.fit_transform(df['y'])
cp = sns.color_palette("hls", n_colors=9+1)
color_y = [cp[x] for x in label_y]
# 都道府県t
label_t = le.fit_transform(df['t'])
cp = sns.color_palette("hls", n_colors=47+1)
color_t = [cp[x] for x in label_t]PCA
from sklearn.decomposition import PCA
pca = PCA()
PC = pca.fit_transform(X)
print(PC.shape)
# (423, 18)
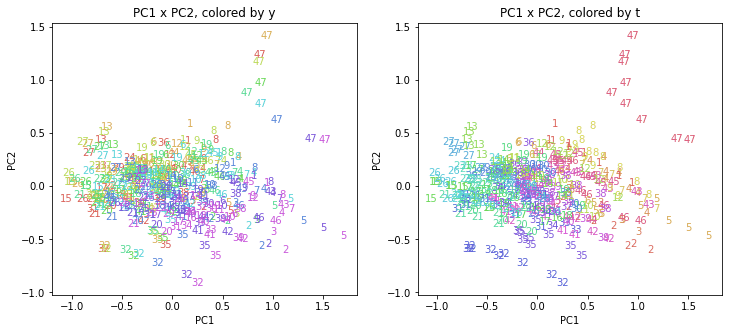






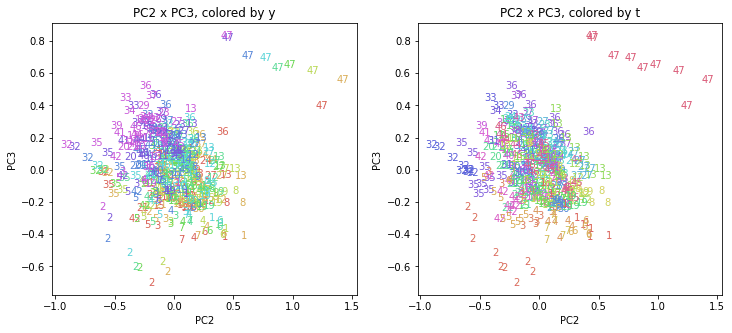












PC1×PC2では、47沖縄がかなり離れたところにあります。
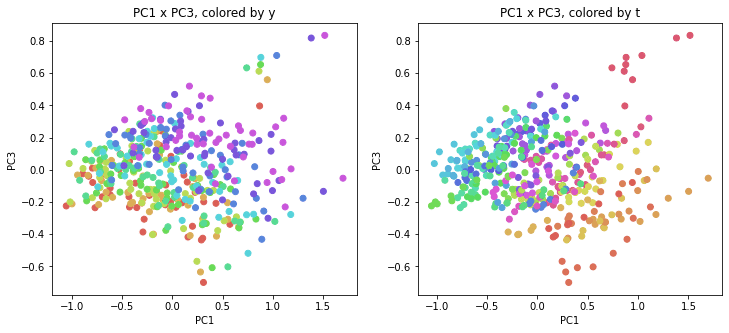
PC1×PC3では、左下から右上に向かって各都道府県が動いている感じです。
UMAP
! pip install umap-learn
import umap.umap_ as umaplist_n_neighbors = [2,3,4,5,10,15,20,30,40,50,60,70,80,90,100,150,200,300,400]
for n_neighbors in list_n_neighbors:
reducer = umap.UMAP(n_components=2, n_neighbors=n_neighbors, random_state=0)
reducer.fit(X)
embedding = reducer.transform(X)
print(embedding.shape) # (423, 2)


















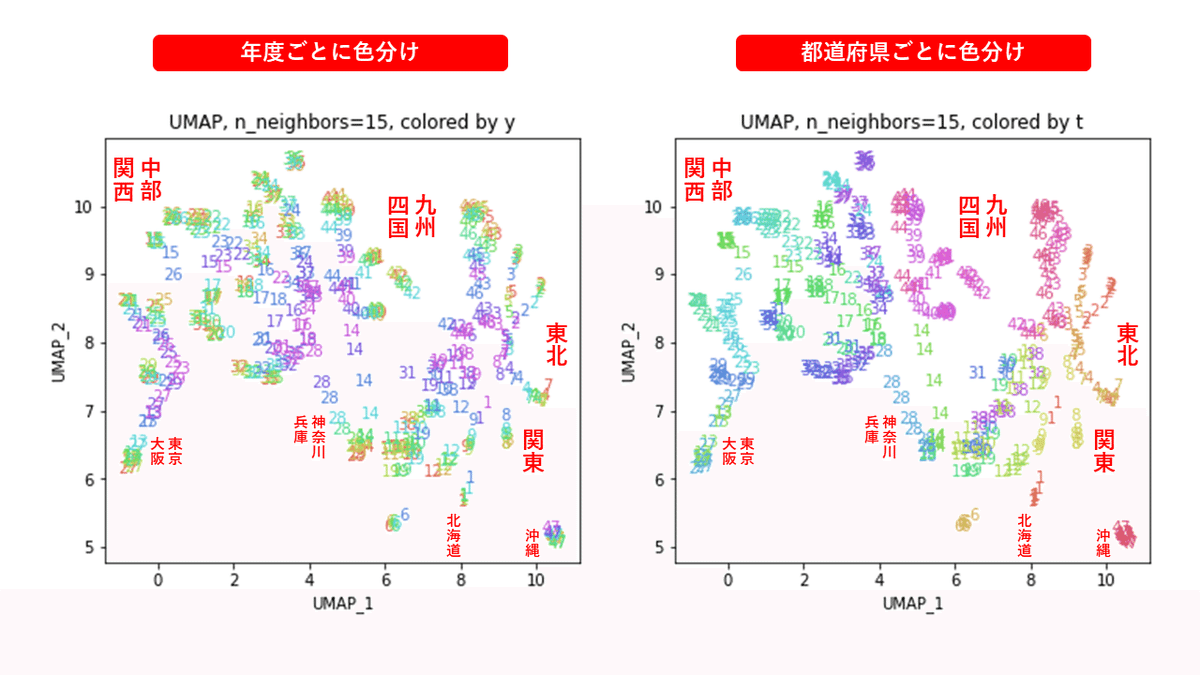
地域性が何となく見えるような気もしますが、医療費データと違って年齢の要素がないためか、あまりきれいな結果にはなっていません。
おわりに
今回は、次元削減のPCAとUMAPの手法を使って、18次元の健診データを2次元に圧縮してみました。
今回使用した健診データは医療費データと違って年齢の要素がなかったためか、あまりきれいな結果にはなりませんでした。
最後まで読んでいただき、ありがとうございました。
お気づきの点等ありましたら、コメントいただけますと幸いです。
#健診 , #医療費分析 , #地域差 , #地域間格差 , #PCA , #UMAP , #機械学習 , #Python , #協会けんぽ , #noteで数式
