
[Python]医療費データを主成分分析してみた
はじめに
こんにちは、機械学習を勉強中の社会人です。初めて投稿します。
医療費の地域間格差に関心があり、機械学習を利用して要因を探りたいと思っています。
今回は、医療費のデータをPCA(主成分分析)してみました。
医療費データの主成分分析
手順
1.データの取得
2.データの加工
3.PCAの実行
4.結果の図示
5.年度単位でPCAの再実行
言語はPython、環境はGoogle Colaboratoryを使用しました。
1.データの取得
データ
医療費に関する手ごろなデータとして、全国健康保険協会(協会けんぽ)のデータを使います。加入者基本情報、医療費基本情報として、2010年度(平成22年度)から直近までの各月のデータが継続して公表されています(3か月分ごとに1ファイル)。
加入者基本情報:
年月・都道府県・適用区分・被保険者被扶養者区分・性別・年齢階級別の加入者数医療費基本情報:
年月・都道府県・被保険者被扶養者区分・性別・年齢階級・診療種別・疾病分類別のレセプト統計の数値:件数、日数、点数、点数(調剤を含む)
それぞれの項目内容の説明はこちらにあります。
使用項目
あまり細かすぎても扱いにくいので、今回は、このうち、年月・都道府県・性別・年齢階級別の診療種別ごとの件数、日数、点数、点数(調剤を含む)を用いることにしました。なお、点数(診療報酬点数)は1点=10円で医療費の金額のことです。
対象期間
新型コロナウイルス感染症の影響が強く出ていると思われる2020(令和2)年度以降のデータを除き、2010(平成22)年4月~2020(令和2)年3月分までの10年間としました。
2.データの加工
データの読み込み
加入者基本情報・医療費基本情報の対象期間のデータをデータフレームに読み込みます。
import pandas as pd
df_P = pd.read_csv('./加入者基本情報.csv', encoding='shift_jis')
df_X = pd.read_csv('./医療費基本情報.csv', encoding='shift_jis')以下、年月をym、都道府県をt、性別をs、年齢階級をn、診療種別をkと表記することにします。また、Pは加入者数(人口)、Xはレセプト統計の数値(件数、日数、点数、点数(調剤含む))を表すことにします。
ym:年月
201004:2010年4月、201005:2010年5月、・・・、202003:2020年3月t:都道府県
1:北海道、2:青森、3:岩手、4:宮城、5:秋田、6:山形、7:福島、8:茨城、9:栃木、10:群馬、11:埼玉、12:千葉、13:東京、14:神奈川、15:新潟、16:富山、17:石川、18:福井、19:山梨、20:長野、21:岐阜、22:静岡、23:愛知、24:三重、25:滋賀、26:京都、27:大阪、28:兵庫、29:奈良、30:和歌山、31:鳥取、32:島根、33:岡山、34:広島、35:山口、36:徳島、37:香川、38:愛媛、39:高知、40:福岡、41:佐賀、42:長崎、43:熊本、44:大分、45:宮崎、46:鹿児島、47:沖縄s:性別
1:男性、2:女性n:年齢10歳階級
1:0~9歳、2:10~20歳、3:20~29歳、4:30~39歳、5:40~49歳、6:50~59歳、7:60~69歳、8:70歳以上k:診療種別
1:医科入院、2:医科外来、3:歯科P:加入者数
X:レセプト統計の数値(医療費に関する集計値)
Ken:件数(レセプトの枚数)、Nit:日数(レセプト上の診療実日数)、Ten:点数(レセプト上の診療報酬点数)、Ten2:点数(調剤含む)(外来レセプトに紐づく調剤レセプトの点数も合計した点数)
データの集計
読み込んだデータから使用する項目のみ抜き出して、集計します。加入者数のデータdf_Pはym,t,s,n,k別に集計し、医療費のデータdf_Xはym,t,s,n,k別に集計して、df_ymtsn_Pとdf_ymtsnk_Xを作成します。df_ymtsn_Pは、ym(10年×12か月)×t(47都道府県)×s(男女の2区分)×n(年齢の8階級)の10×12×47×8=90240行のデータフレーム、df_ymtsnk_Xは、ym(10年×12か月)×t(47都道府県)×s(男女の2区分)×n(年齢の8階級)×k(入院・外来・歯科の3診療種別)の10×12×47×2×8×3=270720行のデータフレームとなります。df_ymtsnk_Xの列は、Ken:件数、Nit:日数、Ten:点数、Ten2:点数(調剤含む)の4項目あります。
df_ymtsn_P = df_P.iloc[:,[0,1,4,5,6]]
col_names = ['ym', 't', 's', 'n', 'P']
df_ymtsn_P.set_axis(col_names, axis='columns', inplace=True)
df_ymtsn_P = df_ymtsn_P.groupby(['ym', 't', 's', 'n'], as_index=False).sum()
df_ymtsnk_X = df_X.iloc[:,[0,1,3,4,5,7,8,9,10]]
col_names = ['ym', 't', 's', 'n', 'k', 'Ken', 'Nit', 'Ten', 'Ten2']
df_ymtsnk_X.set_axis(col_names, axis='columns', inplace=True)
df_ymtsnk_X = df_ymtsnk_X.groupby(['ym', 't', 's', 'n', 'k'], as_index=False).sum()
print(df_ymtsn_P.shape, df_ymtsnk_X.shape)
# (90240, 5) (270720, 9)
# 10*12*47*28, 10*12*47*2*8*3データの変形
次に、df_ymtsnk_Xの行方向のkを列方向に移すことで、df_ymtsn_Pと同じymtsn別の形に変形します。
df_ymtsn_X_k = df_ymtsnk_X.pivot(index=['ym','t','s','n'],
columns=['k'],
values=['Ken','Nit','Ten','Ten2'])
col_names = []
for x in ['Ken','Nit','Ten','Ten2']:
for k in [1,2,3]:
col_names.append(x+'_'+str(k))
df_ymtsn_X_k = df_ymtsn_X_k.set_axis(col_names, axis='columns')
df_ymtsn_X_k = df_ymtsn_X_k.reset_index()
print(df_ymtsn_X_k.columns)
# Index(['ym', 't', 's', 'n', 'Ken_1', 'Ken_2', 'Ken_3', 'Nit_1', 'Nit_2',
# 'Nit_3', 'Ten_1', 'Ten_2', 'Ten_3', 'Ten2_1', 'Ten2_2', 'Ten2_3'],
# dtype='object')
print(df_ymtsn_X_k.shape)
# (90240, 16)これで、医療費のデータもym(10年×12か月)×t(47都道府県)×s(男性・女性の2区分)×n(年齢の8階級)の10×12×47×8=90240行のデータになりました。列の項目は「X_k」(X:数値名、k:診療種別)の形で、例えば、「Ken_1」は「入院の件数」、「Nit_2」は「外来の日数」、「Ten_3」は「歯科の点数」を表しています。
調剤点数の計算
次に、調剤を含む点数Ten2から調剤を含まない点数Tenを引き算することで調剤点数Ten_4を計算します。
df_ymtsn_X_k['Ten_4'] = df_ymtsn_X_k['Ten2_2'] - df_ymtsn_X_k['Ten_2'] + df_ymtsn_X_k['Ten2_3'] - df_ymtsn_X_k['Ten_3']
col_names = ['ym','t','s','n']
for x in ['Ken','Nit','Ten']:
for k in [1,2,3]:
col_names.append(x+'_'+str(k))
col_names = col_names + ['Ten_4']
df_ymtsn_X_k = df_ymtsn_X_k[col_names]
print(df_ymtsn_X_k.columns)
# Index(['ym', 't', 's', 'n', 'Ken_1', 'Ken_2', 'Ken_3', 'Nit_1', 'Nit_2',
# 'Nit_3', 'Ten_1', 'Ten_2', 'Ten_3', 'Ten_4'],
# dtype='object')
print(df_ymtsn_X_k.shape)
# (90240, 14)医療費の3要素の計算
加入者数のデータdf_ymtsn_Pと医療費のデータdf_ymtsn_X_kをym,t,s,n,kごとに突合し、それぞれの加入者数Pと件数Ken、日数Nit、点数Tenから、医療費の3要素を計算します。医療費の3要素とは、
1人当たり件数 = 件数/加入者数(件/人)(「受診率」ということもあります。)
1件当たり日数 = 日数/件数(日/件)
1日当たり点数 = 点数/日数(点/日)
のことで、1人当たり医療費(1人当たり点数)を
1人当たり点数 = 1人当たり件数 × 1件当たり日数 × 1日当たり点数
(点/人) (件/人) (日/件) (点/日)
と分解したものになっています。3要素はそれぞれ分数の形になっていますので、「XperY」(X/Y)の形で表記しています。例えば、「KperP」は「件数Ken/加入者P」で「1人当たり件数」の意味です。
df_ymtsn_XC_k = pd.merge(df_ymtsn_P, df_ymtsn_X_k,
on=['ym','t','s','n'], how='left')
df_ymtsn_XC_k['KperP_1'] = df_ymtsn_XC_k['Ken_1'] / df_ymtsn_XC_k['P']
df_ymtsn_XC_k['KperP_2'] = df_ymtsn_XC_k['Ken_2'] / df_ymtsn_XC_k['P']
df_ymtsn_XC_k['KperP_3'] = df_ymtsn_XC_k['Ken_3'] / df_ymtsn_XC_k['P']
df_ymtsn_XC_k['NperP_1'] = df_ymtsn_XC_k['Nit_1'] / df_ymtsn_XC_k['P']
df_ymtsn_XC_k['NperP_2'] = df_ymtsn_XC_k['Nit_2'] / df_ymtsn_XC_k['P']
df_ymtsn_XC_k['NperP_3'] = df_ymtsn_XC_k['Nit_3'] / df_ymtsn_XC_k['P']
df_ymtsn_XC_k['TperP_1'] = df_ymtsn_XC_k['Ten_1'] / df_ymtsn_XC_k['P']
df_ymtsn_XC_k['TperP_2'] = df_ymtsn_XC_k['Ten_2'] / df_ymtsn_XC_k['P']
df_ymtsn_XC_k['TperP_3'] = df_ymtsn_XC_k['Ten_3'] / df_ymtsn_XC_k['P']
df_ymtsn_XC_k['TperP_4'] = df_ymtsn_XC_k['Ten_4'] / df_ymtsn_XC_k['P']
df_ymtsn_XC_k['NperK_1'] = df_ymtsn_XC_k['Nit_1'] / df_ymtsn_XC_k['Ken_1']
df_ymtsn_XC_k['NperK_2'] = df_ymtsn_XC_k['Nit_2'] / df_ymtsn_XC_k['Ken_2']
df_ymtsn_XC_k['NperK_3'] = df_ymtsn_XC_k['Nit_3'] / df_ymtsn_XC_k['Ken_3']
df_ymtsn_XC_k['TperK_1'] = df_ymtsn_XC_k['Ten_1'] / df_ymtsn_XC_k['Ken_1']
df_ymtsn_XC_k['TperK_2'] = df_ymtsn_XC_k['Ten_2'] / df_ymtsn_XC_k['Ken_2']
df_ymtsn_XC_k['TperK_3'] = df_ymtsn_XC_k['Ten_3'] / df_ymtsn_XC_k['Ken_3']
df_ymtsn_XC_k['TperK_4'] = df_ymtsn_XC_k['Ten_4'] / df_ymtsn_XC_k['Ken_2']
df_ymtsn_XC_k['TperN_1'] = df_ymtsn_XC_k['Ten_1'] / df_ymtsn_XC_k['Nit_1']
df_ymtsn_XC_k['TperN_2'] = df_ymtsn_XC_k['Ten_2'] / df_ymtsn_XC_k['Nit_2']
df_ymtsn_XC_k['TperN_3'] = df_ymtsn_XC_k['Ten_3'] / df_ymtsn_XC_k['Nit_3']
df_ymtsn_XC_k['TperN_4'] = df_ymtsn_XC_k['Ten_4'] / df_ymtsn_XC_k['Nit_2']
print(df_ymtsn_XC_k.columns)
# Index(['ym', 't', 's', 'n', 'P', 'Ken_1', 'Ken_2', 'Ken_3', 'Nit_1', 'Nit_2',
# 'Nit_3', 'Ten_1', 'Ten_2', 'Ten_3', 'Ten_4', 'KperP_1', 'KperP_2',
# 'KperP_3', 'NperP_1', 'NperP_2', 'NperP_3', 'TperP_1', 'TperP_2',
# 'TperP_3', 'TperP_4', 'NperK_1', 'NperK_2', 'NperK_3', 'TperK_1',
# 'TperK_2', 'TperK_3', 'TperK_4', 'TperN_1', 'TperN_2', 'TperN_3',
# 'TperN_4'],
# dtype='object')
print(df_ymtsn_XC_k.shape)
# (90240, 36)
col_names = ['ym','t','s','n']
var_names = []
for x in ['KperP','NperK','TperN']:
if x != 'TperN':
for k in [1,2,3]:
var_names.append(x+'_'+str(k))
else:
for k in [1,2,3,4]:
var_names.append(x+'_'+str(k))
col_names = col_names + var_names
df_ymtsn_C10 = df_ymtsn_XC_k.copy()
df_ymtsn_C10 = df_ymtsn_C10[col_names]
print(df_ymtsn_C10.columns)
# Index(['ym', 't', 's', 'n', 'KperP_1', 'KperP_2', 'KperP_3', 'NperK_1',
# 'NperK_2', 'NperK_3', 'TperN_1', 'TperN_2', 'TperN_3', 'TperN_4'],
# dtype='object')
print(df_ymtsn_C10.shape)
# (90240, 14)これで、ymtsn別の診療種別ごとの3要素(入院・外来・歯科の1人当たり件数、入院・外来・歯科の1件当たり日数、入院・外来・歯科・調剤の1日当たり点数の計10項目)が計算できました。
データの完成形
さらに、これをymt別の形に変形します。項目名は、「XperY_k_s_n」(XperY:要素名、k:診療種別、s:性別、n:年齢階級)の形で、例えば、「KperP_1_2_3」は「1人当たり件数_入院_女性_20歳代」の意味、「NperK_3_1_2」は「1件当たり日数_歯科_男性_10歳代」の意味です。
df_ymt_C10_sn = df_ymtsn_C10.pivot(index=['ym','t'],
columns=['s','n'],
values=var_names)
col_names = []
for ck in var_names:
for s in [1,2]:
for n in [1,2,3,4,5,6,7,8]:
# print(ck+'_'+str(s)+'_'+str(n))
col_names.append(ck+'_'+str(s)+'_'+str(n))
df_ymt_C10_sn = df_ymt_C10_sn.set_axis(col_names, axis='columns')
df_ymt_C10_sn = df_ymt_C10_sn.reset_index()
print(df_ymt_C10_sn.columns)
# Index(['ym', 't', 'KperP_1_1_1', 'KperP_1_1_2', 'KperP_1_1_3', 'KperP_1_1_4',
# 'KperP_1_1_5', 'KperP_1_1_6', 'KperP_1_1_7', 'KperP_1_1_8',
# ...
# 'TperN_4_1_7', 'TperN_4_1_8', 'TperN_4_2_1', 'TperN_4_2_2',
# 'TperN_4_2_3', 'TperN_4_2_4', 'TperN_4_2_5', 'TperN_4_2_6',
# 'TperN_4_2_7', 'TperN_4_2_8'],
# dtype='object', length=162)
print(df_ymt_C10_sn.shape)
# (5640, 162)これで、ym,t別の医療費3要素のデータができました。
3.PCAの実行
このデータを用いて、PCA(主成分分析)を実行します。
ym,tの2列を除いて数値部分のみ取り出したデータは、10年×12か月×47都道府県=5640行、診療種別ごとの3要素10項目×性別2区分×年齢8階級=160列の形になっています。
df = df_ymt_C10_sn.copy()
X = df.iloc[:,2:] # 数値部分のみ
print(X.shape)
# (5640, 160)
# 5640=10*12*47, 160=10*2*8前処理
スケールの異なる3要素のデータなので、前処理としてスケーリングしておきます。StandardScalerとMinMaxScalerの両方を試してみて、後者の方が結果がよかったのでMinMaxScalerを使いました。
from sklearn import preprocessing
scaler = preprocessing.StandardScaler()
X = scaler.fit_transform(X)
scaler = preprocessing.MinMaxScaler()
X = scaler.fit_transform(X)
print(X.shape)
# (5640, 160)PCA
scikit-learnのdecomposition.PCAを使って主成分分析を実行します。
from sklearn.decomposition import PCA
pca = PCA(n_components=160)
PC = pca.fit_transform(X)
print(PC.shape)
# (5640, 160)寄与率
累積寄与率を見ると、第10主成分までで8割を超えていました。
import numpy as np
np.set_printoptions(precision=5, suppress=True) # numpyの表示桁数設定
print(pca.explained_variance_ratio_) # 寄与率
# [0.40023 0.12229 0.07477 0.05272 0.0466 0.03249 0.02905 0.02144 0.01569
# 0.01499 0.0117 0.00901 0.00791 0.00716 0.0062 0.00534 0.0052 0.00469
# 0.00438 0.00412 0.00393 0.00385 0.00356 0.00323 0.0032 0.00305 0.00296
# 0.00288 0.00281 0.00266 0.00264 0.00247 0.00235 0.00234 0.00227 0.00215
# 0.00211 0.00202 0.00197 0.00191 0.00182 0.00174 0.00165 0.00162 0.0016
# 0.00156 0.00153 0.00152 0.00141 0.00139 0.00136 0.00133 0.00132 0.00127
# 0.00123 0.00122 0.00117 0.00117 0.00113 0.00111 0.00109 0.00109 0.00107
# 0.00105 0.00101 0.00099 0.00096 0.00094 0.00093 0.0009 0.00088 0.00085
# 0.00083 0.00082 0.00079 0.00076 0.00075 0.00073 0.00071 0.00071 0.0007
# 0.00068 0.00067 0.00066 0.00065 0.00063 0.00061 0.0006 0.00059 0.00057
# 0.00057 0.00055 0.00054 0.00052 0.00052 0.00051 0.0005 0.00049 0.00049
# 0.00046 0.00044 0.00043 0.00041 0.0004 0.00039 0.00038 0.00037 0.00037
# 0.00036 0.00035 0.00033 0.00033 0.00032 0.0003 0.00029 0.00028 0.00027
# 0.00026 0.00025 0.00024 0.00024 0.00024 0.00023 0.00022 0.00022 0.00022
# 0.0002 0.0002 0.00019 0.00018 0.00018 0.00018 0.00017 0.00016 0.00015
# 0.00014 0.00014 0.00014 0.00014 0.00013 0.00013 0.00012 0.00012 0.00011
# 0.00011 0.00011 0.0001 0.0001 0.0001 0.00009 0.00008 0.00008 0.00008
# 0.00007 0.00007 0.00005 0.00005 0.00005 0.00004 0.00004]
print(np.cumsum(pca.explained_variance_ratio_)) # 累積寄与率
# [0.40023 0.52252 0.5973 0.65002 0.69662 0.72911 0.75816 0.7796 0.7953
# 0.81029 0.82198 0.83099 0.8389 0.84606 0.85227 0.85761 0.86281 0.86749
# 0.87187 0.87599 0.87993 0.88378 0.88734 0.89057 0.89378 0.89683 0.89979
# 0.90266 0.90547 0.90813 0.91077 0.91324 0.9156 0.91794 0.92021 0.92236
# 0.92447 0.92649 0.92845 0.93036 0.93218 0.93392 0.93556 0.93718 0.93878
# 0.94033 0.94187 0.94339 0.9448 0.94619 0.94755 0.94888 0.95019 0.95146
# 0.95269 0.9539 0.95508 0.95624 0.95737 0.95849 0.95958 0.96067 0.96173
# 0.96278 0.96379 0.96479 0.96575 0.96669 0.96763 0.96853 0.96941 0.97026
# 0.97108 0.97191 0.97269 0.97346 0.97421 0.97494 0.97566 0.97636 0.97706
# 0.97774 0.97841 0.97907 0.97973 0.98036 0.98097 0.98158 0.98216 0.98274
# 0.9833 0.98385 0.9844 0.98492 0.98544 0.98594 0.98644 0.98694 0.98742
# 0.98789 0.98833 0.98876 0.98917 0.98957 0.98995 0.99033 0.99071 0.99108
# 0.99143 0.99178 0.99211 0.99244 0.99276 0.99306 0.99335 0.99362 0.9939
# 0.99416 0.99441 0.99465 0.99489 0.99513 0.99536 0.99558 0.9958 0.99602
# 0.99622 0.99642 0.99661 0.99679 0.99697 0.99715 0.99732 0.99747 0.99763
# 0.99777 0.99791 0.99805 0.99819 0.99832 0.99844 0.99856 0.99868 0.99879
# 0.9989 0.999 0.9991 0.9992 0.9993 0.99938 0.99947 0.99955 0.99962
# 0.99969 0.99976 0.99981 0.99987 0.99992 0.99996 1. ]4.結果の図示
年月別・都道府県別の色分け
以下、PCAの結果の第n主成分をPCnと表記します。
PCAの結果を見やすく表示するため、seabornのカラーパレットを使って、年月別、都道府県別に色分けして図示してみます(左側が年月別に色分け、右側が都道府県別に色分け)。PC1~PC10まで表示しました。
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import preprocessing
le = preprocessing.LabelEncoder()
# 年月ym
label_ym = le.fit_transform(df['ym'])
cp = sns.color_palette("hls", n_colors=10*12+1)
color_ym = [cp[x] for x in label_ym]
# 都道府県t
label_t = le.fit_transform(df['t'])
cp = sns.color_palette("hls", n_colors=47+1)
color_t = [cp[x] for x in label_t]
n = 10
for i in range(n-1):
for j in range(i+1,n):
print('PC{} x PC{}'.format(i+1, j+1))
plt.figure(figsize=(12,5))
plt.subplot(1, 2, 1)
plt.title('PC{} x PC{} colored by ym'.format(i+1, j+1))
plt.xlabel('PC{}'.format(i+1))
plt.ylabel('PC{}'.format(j+1))
plt.scatter(x=PC[:,i], y=PC[:,j], c=color_ym, s=10, alpha=0.5)
plt.subplot(1, 2, 2)
plt.title('PC{} x PC{} colored by t'.format(i+1, j+1))
plt.xlabel('PC{}'.format(i+1))
plt.ylabel('PC{}'.format(j+1))
plt.scatter(x=PC[:,i], y=PC[:,j], c=color_t, s=10, alpha=0.5)
plt.show()





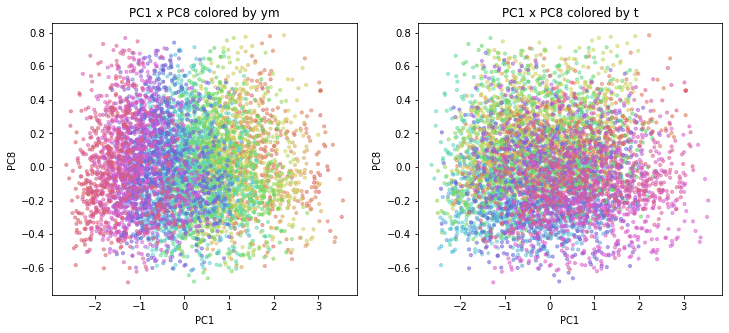










PC1×PCn(n>1)を見ると、左側の図(年月で色分け)ではPC1方向に色が変わっており、右側の図(都道府県で色分け)ではPC1方向に同じ色が並んでいます。
PC2×PC3以降を見ると、左側の図(年月で色分け)では年月の色が混ざっており、右側の図(都道府県で色分け)では同じ色が固まって存在しています。
このことから、PC1は時間の経過を表す成分(時間軸)、PC2以降は時点によって変わらない何らかの地域的な特徴を表す成分のようです。
(PC2×PC3の右側の図(都道府県で色分け)では、同系色の色が近くに分布していることから、都道府県番号の近い(=地理的に近い)都道府県が近い主成分値となっているので、何らかの地理的な特徴を表していると考えられます。)
都道府県番号の表示
上の色分けだけでは都道府県が区別しにくいので、点の代わりに都道府県番号をプロットした図も描いておきます(色分けは上と同じ)。
n = 5
for i in range(n):
for j in range(i+1,n):
if (i==0 or j==i+1):
print('PC{} x PC{}'.format(i+1, j+1))
xmin, xmax = min(PC[:,i]), max(PC[:,i])
ymin, ymax = min(PC[:,j]), max(PC[:,j])
plt.figure(figsize=(16,7))
plt.subplot(1, 2, 1)
plt.title('PC{} x PC{}, colored by ym'.format(i+1, j+1))
plt.xlabel('PC{}'.format(i+1))
plt.ylabel('PC{}'.format(j+1))
plt.xlim(xmin-(xmax-xmin)/20, xmax+(xmax-xmin)/20)
plt.ylim(ymin-(ymax-ymin)/20, ymax+(ymax-ymin)/20)
for p in range(10*12*47):
plt.text(x=PC[:,i][p], y=PC[:,j][p], s=df.iloc[:,1][p],
ha='center', va='center', fontsize=10, color=color_ym[p])
plt.subplot(1, 2, 2)
plt.title('PC{} x PC{}, colored by t'.format(i+1, j+1))
plt.xlabel('PC{}'.format(i+1))
plt.ylabel('PC{}'.format(j+1))
plt.xlim(xmin-(xmax-xmin)/20, xmax+(xmax-xmin)/20)
plt.ylim(ymin-(ymax-ymin)/20, ymax+(ymax-ymin)/20)
for p in range(10*12*47):
plt.text(x=PC[:,i][p], y=PC[:,j][p], s=df.iloc[:,1][p],
ha='center', va='center', fontsize=10, color=color_t[p])
plt.show()



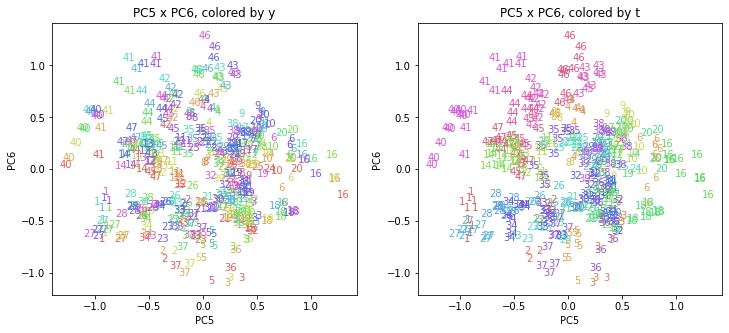
同じ都道府県の番号はある程度固まって近くに分布しています。
PC2は、1北海道、47沖縄が高く、23愛知、27大阪が低くなっています。PC3は、41佐賀、36徳島が高く、20長野、11埼玉、12千葉が低くなっています。PC4は、18福井、33岡山、29奈良が高くなっています。
5.年度単位でPCAの再実行
年月単位ではデータが多すぎてプロットが重なって見づらくなってしまいましたので、年度単位に集計し直して再度PCAを実行することにしました。
年度単位の集計
年月ymから年度yを計算して追加し、ym別の集計だったところをy別に集計し直します。
# 年度追加
df_ymtsn_P['y'] = df_ymtsn_P['ym'] // 100
df_ymtsn_P['y'] = df_ymtsn_P['y'].where(df_ymtsn_P['ym'] % 100 >= 4, df_ymtsn_P['y']-1)
df_ymtsnk_X['y'] = df_ymtsnk_X['ym'] // 100
df_ymtsnk_X['y'] = df_ymtsnk_X['y'].where(df_ymtsnk_X['ym'] % 100 >= 4, df_ymtsnk_X['y']-1)
print(df_ymtsn_P.shape, df_ymtsnk_X.shape)
# (90240, 6) (270720, 10)
# 年度集計
df_ytsn_P = df_ymtsn_P.loc[:,['y','t','s','n','P']]
df_ytsn_P = df_ytsn_P.groupby(['y','t','s','n'], as_index=False).sum()
df_ytsnk_X = df_ymtsnk_X.loc[:,['y','t','s','n','k','Ken','Nit','Ten','Ten2']]
df_ytsnk_X = df_ytsnk_X.groupby(['y','t','s','n','k'], as_index=False).sum()
print(df_ytsn_P.shape, df_ytsnk_X.shape)
# (7520, 5) (22560, 9)
# 医療費データのpivot
df_ytsn_X_k = df_ytsnk_X.pivot(index=['y','t','s','n'],
columns=['k'],
values=['Ken','Nit','Ten','Ten2'])
col_names = []
for x in ['Ken','Nit','Ten','Ten2']:
for k in [1,2,3]:
col_names.append(x+'_'+str(k))
df_ytsn_X_k = df_ytsn_X_k.set_axis(col_names, axis='columns')
df_ytsn_X_k = df_ytsn_X_k.reset_index()
print(df_ytsn_X_k.columns)
# Index(['y', 't', 's', 'n', 'Ken_1', 'Ken_2', 'Ken_3', 'Nit_1', 'Nit_2',
# 'Nit_3', 'Ten_1', 'Ten_2', 'Ten_3', 'Ten2_1', 'Ten2_2', 'Ten2_3'],
# dtype='object')
print(df_ytsn_X_k.shape)
# (7520, 16)
# 調剤点数計算
df_ytsn_X_k['Ten_4'] = df_ytsn_X_k['Ten2_2'] - df_ytsn_X_k['Ten_2'] + df_ytsn_X_k['Ten2_3'] - df_ytsn_X_k['Ten_3']
col_names = ['y','t','s','n']
for x in ['Ken','Nit','Ten']:
for k in [1,2,3]:
col_names.append(x+'_'+str(k))
col_names = col_names + ['Ten_4']
df_ytsn_X_k = df_ytsn_X_k[col_names]
print(df_ytsn_X_k.columns)
# Index(['y', 't', 's', 'n', 'Ken_1', 'Ken_2', 'Ken_3', 'Nit_1', 'Nit_2',
# 'Nit_3', 'Ten_1', 'Ten_2', 'Ten_3', 'Ten_4'],
# dtype='object')
print(df_ytsn_X_k.shape)
# (7520, 14)
# 医療費の3要素の計算
df_ytsn_XC_k = pd.merge(df_ytsn_P, df_ytsn_X_k,
on=['y','t','s','n'], how='left')
df_ytsn_XC_k['KperP_1'] = df_ytsn_XC_k['Ken_1'] /(df_ytsn_XC_k['P']/12)
df_ytsn_XC_k['KperP_2'] = df_ytsn_XC_k['Ken_2'] /(df_ytsn_XC_k['P']/12)
df_ytsn_XC_k['KperP_3'] = df_ytsn_XC_k['Ken_3'] /(df_ytsn_XC_k['P']/12)
df_ytsn_XC_k['NperP_1'] = df_ytsn_XC_k['Nit_1'] /(df_ytsn_XC_k['P']/12)
df_ytsn_XC_k['NperP_2'] = df_ytsn_XC_k['Nit_2'] /(df_ytsn_XC_k['P']/12)
df_ytsn_XC_k['NperP_3'] = df_ytsn_XC_k['Nit_3'] /(df_ytsn_XC_k['P']/12)
df_ytsn_XC_k['TperP_1'] = df_ytsn_XC_k['Ten_1'] /(df_ytsn_XC_k['P']/12)
df_ytsn_XC_k['TperP_2'] = df_ytsn_XC_k['Ten_2'] /(df_ytsn_XC_k['P']/12)
df_ytsn_XC_k['TperP_3'] = df_ytsn_XC_k['Ten_3'] /(df_ytsn_XC_k['P']/12)
df_ytsn_XC_k['TperP_4'] = df_ytsn_XC_k['Ten_4'] /(df_ytsn_XC_k['P']/12)
df_ytsn_XC_k['NperK_1'] = df_ytsn_XC_k['Nit_1'] / df_ytsn_XC_k['Ken_1']
df_ytsn_XC_k['NperK_2'] = df_ytsn_XC_k['Nit_2'] / df_ytsn_XC_k['Ken_2']
df_ytsn_XC_k['NperK_3'] = df_ytsn_XC_k['Nit_3'] / df_ytsn_XC_k['Ken_3']
df_ytsn_XC_k['TperK_1'] = df_ytsn_XC_k['Ten_1'] / df_ytsn_XC_k['Ken_1']
df_ytsn_XC_k['TperK_2'] = df_ytsn_XC_k['Ten_2'] / df_ytsn_XC_k['Ken_2']
df_ytsn_XC_k['TperK_3'] = df_ytsn_XC_k['Ten_3'] / df_ytsn_XC_k['Ken_3']
df_ytsn_XC_k['TperK_4'] = df_ytsn_XC_k['Ten_4'] / df_ytsn_XC_k['Ken_2']
df_ytsn_XC_k['TperN_1'] = df_ytsn_XC_k['Ten_1'] / df_ytsn_XC_k['Nit_1']
df_ytsn_XC_k['TperN_2'] = df_ytsn_XC_k['Ten_2'] / df_ytsn_XC_k['Nit_2']
df_ytsn_XC_k['TperN_3'] = df_ytsn_XC_k['Ten_3'] / df_ytsn_XC_k['Nit_3']
df_ytsn_XC_k['TperN_4'] = df_ytsn_XC_k['Ten_4'] / df_ytsn_XC_k['Nit_2']
print(df_ytsn_XC_k.columns)
# Index(['y', 't', 's', 'n', 'P', 'Ken_1', 'Ken_2', 'Ken_3', 'Nit_1', 'Nit_2',
# 'Nit_3', 'Ten_1', 'Ten_2', 'Ten_3', 'Ten_4', 'KperP_1', 'KperP_2',
# 'KperP_3', 'NperP_1', 'NperP_2', 'NperP_3', 'TperP_1', 'TperP_2',
# 'TperP_3', 'TperP_4', 'NperK_1', 'NperK_2', 'NperK_3', 'TperK_1',
# 'TperK_2', 'TperK_3', 'TperK_4', 'TperN_1', 'TperN_2', 'TperN_3',
# 'TperN_4'],
# dtype='object')
print(df_ytsn_XC_k.shape)
# (7520, 36)
col_names = ['y','t','s','n']
var_names = []
for x in ['KperP','NperK','TperN']:
if x != 'TperN':
for k in [1,2,3]:
var_names.append(x+'_'+str(k))
else:
for k in [1,2,3,4]:
var_names.append(x+'_'+str(k))
col_names = col_names + var_names
df_ytsn_C10 = df_ytsn_XC_k.copy()
df_ytsn_C10 = df_ytsn_C10[col_names]
print(df_ytsn_C10.columns)
# Index(['y', 't', 's', 'n', 'KperP_1', 'KperP_2', 'KperP_3', 'NperK_1',
# 'NperK_2', 'NperK_3', 'TperN_1', 'TperN_2', 'TperN_3', 'TperN_4'],
# dtype='object')
print(df_ytsn_C10.shape)
# (7520, 14)
# データのpivot
df_yt_C10_sn = df_ytsn_C10.pivot(index=['y','t'],
columns=['s','n'],
values=var_names)
col_names = []
for ck in var_names:
for s in [1,2]:
for n in [1,2,3,4,5,6,7,8]:
col_names.append(ck+'_'+str(s)+'_'+str(n))
df_yt_C10_sn = df_yt_C10_sn.set_axis(col_names, axis='columns')
df_yt_C10_sn = df_yt_C10_sn.reset_index()
print(df_yt_C10_sn.columns)
# Index(['y', 't', 'KperP_1_1_1', 'KperP_1_1_2', 'KperP_1_1_3', 'KperP_1_1_4',
# 'KperP_1_1_5', 'KperP_1_1_6', 'KperP_1_1_7', 'KperP_1_1_8',
# ...
# 'TperN_4_1_7', 'TperN_4_1_8', 'TperN_4_2_1', 'TperN_4_2_2',
# 'TperN_4_2_3', 'TperN_4_2_4', 'TperN_4_2_5', 'TperN_4_2_6',
# 'TperN_4_2_7', 'TperN_4_2_8'],
# dtype='object', length=162)
print(df_yt_C10_sn.shape)
# (470, 162)1件当たり件数(受診率)の計算は、12か月分の加入者数Pを12で割った年度平均加入者数で割って計算しています。
これで、yt別の医療費3要素のデータができました。
PCAの実行
このデータに対して、上と同様にPCAを実行します。
y,tの2列を除いて数値部分のみ取り出したデータは、10年×47都道府県=470行、診療種別ごとの3要素10項目×性別2区分×年齢8階級=160列の形になっています。
df = df_yt_C10_sn.copy()
X = df.iloc[:,2:] # 数値部分のみ
print(X.shape)
# (470, 160)
# 前処理
scaler = preprocessing.StandardScaler()
X = scaler.fit_transform(X)
scaler = preprocessing.MinMaxScaler()
X = scaler.fit_transform(X)
print(X.shape)
# (470, 160)
# PCA
from sklearn.decomposition import PCA
pca = PCA(n_components=160)
PC = pca.fit_transform(X)
print(PC.shape)
# (470, 160)PCAの結果
累積寄与率は第6主成分までで8割を超えました。
# 寄与率
print(pca.explained_variance_ratio_) # 寄与率
# [0.44787 0.1282 0.09443 0.05171 0.0431 0.0373 0.02687 0.02205 0.01517
# 0.00986 0.00909 0.0085 0.00776 0.00697 0.00598 0.00502 0.00463 0.00452
# 0.00396 0.00364 0.00353 0.00301 0.00295 0.00259 0.00244 0.00237 0.00213
# 0.00202 0.00193 0.00187 0.00174 0.0016 0.00148 0.00134 0.00132 0.00129
# 0.00119 0.00118 0.00109 0.00105 0.00097 0.0009 0.00088 0.00085 0.00081
# 0.00078 0.00074 0.0007 0.00068 0.00066 0.00063 0.0006 0.00057 0.00056
# 0.00054 0.00053 0.00051 0.00047 0.00046 0.00046 0.00043 0.00041 0.0004
# 0.00038 0.00038 0.00037 0.00034 0.00033 0.00032 0.00031 0.00029 0.00028
# 0.00027 0.00027 0.00026 0.00025 0.00024 0.00023 0.00023 0.00022 0.00021
# 0.0002 0.0002 0.0002 0.00019 0.00018 0.00018 0.00017 0.00016 0.00016
# 0.00015 0.00015 0.00014 0.00014 0.00013 0.00013 0.00013 0.00012 0.00012
# 0.00012 0.00011 0.00011 0.0001 0.0001 0.00009 0.00009 0.00009 0.00008
# 0.00008 0.00008 0.00008 0.00007 0.00007 0.00007 0.00007 0.00006 0.00006
# 0.00006 0.00006 0.00005 0.00005 0.00005 0.00005 0.00005 0.00004 0.00004
# 0.00004 0.00004 0.00004 0.00003 0.00003 0.00003 0.00003 0.00003 0.00003
# 0.00003 0.00003 0.00002 0.00002 0.00002 0.00002 0.00002 0.00002 0.00002
# 0.00002 0.00002 0.00002 0.00001 0.00001 0.00001 0.00001 0.00001 0.00001
# 0.00001 0.00001 0.00001 0.00001 0.00001 0.00001 0.00001]
print(np.cumsum(pca.explained_variance_ratio_)) # 累積寄与率
# [0.44787 0.57607 0.67051 0.72222 0.76532 0.80262 0.82949 0.85153 0.86671
# 0.87656 0.88565 0.89416 0.90192 0.90889 0.91487 0.9199 0.92453 0.92904
# 0.93301 0.93665 0.94018 0.94319 0.94614 0.94873 0.95118 0.95355 0.95568
# 0.9577 0.95963 0.96151 0.96325 0.96485 0.96632 0.96767 0.96899 0.97028
# 0.97146 0.97264 0.97373 0.97478 0.97575 0.97665 0.97753 0.97838 0.97919
# 0.97997 0.98071 0.98141 0.98209 0.98275 0.98338 0.98398 0.98455 0.9851
# 0.98565 0.98618 0.98669 0.98717 0.98763 0.98809 0.98852 0.98893 0.98933
# 0.98971 0.99009 0.99046 0.9908 0.99113 0.99144 0.99175 0.99204 0.99232
# 0.99259 0.99286 0.99312 0.99336 0.9936 0.99383 0.99406 0.99429 0.9945
# 0.9947 0.9949 0.9951 0.99529 0.99547 0.99565 0.99582 0.99598 0.99613
# 0.99629 0.99644 0.99658 0.99671 0.99685 0.99698 0.9971 0.99722 0.99734
# 0.99746 0.99757 0.99768 0.99778 0.99788 0.99797 0.99806 0.99814 0.99823
# 0.99831 0.99839 0.99847 0.99854 0.99861 0.99868 0.99875 0.99881 0.99887
# 0.99893 0.99899 0.99904 0.99909 0.99914 0.99919 0.99924 0.99928 0.99932
# 0.99937 0.9994 0.99944 0.99947 0.99951 0.99954 0.99957 0.9996 0.99963
# 0.99965 0.99968 0.9997 0.99973 0.99975 0.99977 0.99979 0.99981 0.99982
# 0.99984 0.99986 0.99987 0.99989 0.9999 0.99991 0.99992 0.99993 0.99994
# 0.99995 0.99996 0.99997 0.99998 0.99999 0.99999 1. ]結果の図示
また、上と同様に、年度別(左側の図)、都道府県別(右側の図)に色分けしてみます。
le = preprocessing.LabelEncoder()
# 年度y
label_y = le.fit_transform(df['y'])
cp = sns.color_palette("hls", n_colors=10+1)
color_y = [cp[x] for x in label_y]
# 都道府県t
label_t = le.fit_transform(df['t'])
cp = sns.color_palette("hls", n_colors=47+1)
color_t = [cp[x] for x in label_t]
n = 10
for i in range(n-1):
j = i+1
print('PC{} x PC{}'.format(i+1, j+1))
plt.figure(figsize=(12,5))
plt.subplot(1, 2, 1)
plt.title('PC{} x PC{} colored by y'.format(i+1, j+1))
plt.xlabel('PC{}'.format(i+1))
plt.ylabel('PC{}'.format(j+1))
plt.scatter(x=PC[:,i], y=PC[:,j], c=color_y)
plt.subplot(1, 2, 2)
plt.title('PC{} x PC{} colored by t'.format(i+1, j+1))
plt.xlabel('PC{}'.format(i+1))
plt.ylabel('PC{}'.format(j+1))
plt.scatter(x=PC[:,i], y=PC[:,j], c=color_t)
plt.show()








PC5くらいまでは、年月単位で実行した主成分の結果と似ているように見えます。
都道府県番号の表示
上と同様に、点の代わりに都道府県番号もプロットしておきます。
n = 10
for i in range(n):
for j in range(i+1,n):
if (i==0 or j==i+1):
print('PC{} x PC{}'.format(i+1, j+1))
xmin, xmax = min(PC[:,i]), max(PC[:,i])
ymin, ymax = min(PC[:,j]), max(PC[:,j])
plt.figure(figsize=(12,5))
plt.subplot(1, 2, 1)
plt.title('PC{} x PC{}, colored by y'.format(i+1, j+1))
plt.xlabel('PC{}'.format(i+1))
plt.ylabel('PC{}'.format(j+1))
plt.xlim(xmin-(xmax-xmin)/20, xmax+(xmax-xmin)/20)
plt.ylim(ymin-(ymax-ymin)/20, ymax+(ymax-ymin)/20)
for p in range(10*47):
plt.text(x=PC[:,i][p], y=PC[:,j][p], s=df.iloc[:,1][p],
ha='center', va='center', fontsize=10, color=color_y[p])
plt.subplot(1, 2, 2)
plt.title('PC{} x PC{}, colored by t'.format(i+1, j+1))
plt.xlabel('PC{}'.format(i+1))
plt.ylabel('PC{}'.format(j+1))
plt.xlim(xmin-(xmax-xmin)/20, xmax+(xmax-xmin)/20)
plt.ylim(ymin-(ymax-ymin)/20, ymax+(ymax-ymin)/20)
for p in range(10*47):
plt.text(x=PC[:,i][p], y=PC[:,j][p], s=df.iloc[:,1][p],
ha='center', va='center', fontsize=10, color=color_t[p])
plt.show()















PC1×PCn(n>1)を見ると、都道府県番号はお互いの相対的な位置関係を保ったまま全体としてPC1軸に沿って平行移動しています。PCn×PCm(n>1,m>1)を見ると、同じ都道府県番号はほとんど位置を変えずに固まっています。
PC1は時間の経過、PC2以降は何らかの地域の特徴を表す成分で、その地域の特徴は年度によってほとんど変わっていないということがよりはっきりわかるようになりました。
おわりに
PCAの結果、第1主成分は時間の経過を表す成分で、時間軸に沿った全体的な動き(全国的な動き)を表しており、第2主成分以降は、地域の特徴を表す成分で、この10年間ほとんど変わっていないことがわかりました。第2主成分以降がそれぞれ具体的に何を表すのかの解釈はできていませんが、これほどはっきりと地域の特徴を表す成分を抽出できたのは驚きでした。
この10年間で、医療保険制度をめぐって様々な状況の変化がありました。医療提供側の行動や患者の受診行動に影響を与えそうなものとして、診療報酬改定・薬価改定(2年ごと)、消費税増税(2019(平成27)年10月)、大規模な医療保険制度改革(2018(平成30)年度)、短時間労働者への適用拡大、高額療養費制度の改正、自己負担割合の変更、東日本大震災(2011(平成23)年3月11日)・熊本地震(2016(平成28)年4月14・16日)等の自然災害、ジェネリック医薬品の使用割合の向上、DPC制度の進展、などなど。それにもかかわらず、これほどはっきりと変わらない地域の特徴を表す成分が抽出できたということは、都道府県の医療費の構造にそれほど根深い違いが存在しているということかもしれません。
今回は、協会けんぽの医療費データを使ってPCAを試してみました。今後、他の手法も試してみたいと思います。
また、都道府県間の違いが大きいということは、医療費のデータから都道府県を予測できそうな気がしますので、分類問題として解いてみようと思います。
最後まで読んでいただき、ありがとうございました。
お気づきの点等ありましたら、コメントいただけますと幸いです。
