AIエンジニアへの道：パーセプトロンってなに？

はじめに：AIエンジニアへの道を歩む理由

こんにちは、AIスタートアップのPdMとして働いている私ですが、
新たな挑戦としてAIエンジニアとしてのスキルを身につけることに挑戦中！
「なんでAIエンジニア？」と思われるかもしれませんが、スタートアップの現場で毎日感じるのは、テクノロジーが世界を変える力。その最前線にいる中で、動きを理解し「自分でも作れるようになりたい！」と思い、学習を始めました🦖

今日は、その第一歩として「パーセプトロン」について一緒に学んでいきましょう！
初心者でも楽しく学べるように、できるだけわかりやすくお伝えしていきますので、お付き合いくださいね🙌🏻💫

パーセプトロンとは？ — 知識の第一歩

パーセプトロンという言葉、皆さんは聞いたことがありますか？
名前だけ聞くとなんだか難しそうですが、、、
実はAIのアルゴリズムの中でも基礎中の基礎。この「パーセプトロン」があってこそ、今のAI技術が存在していると言っても過言ではありません。

簡単に言うと、
パーセプトロンは、データから「YES」か「NO」かを判断する最も単純なアルゴリズムです。
まるで電気のスイッチのように、入力に対して一つの答えを出す仕組みです。高校生でも理解できるように例えるなら、電気を通すか通さないかのスイッチがあって、それを使って「AI」が簡単な判断を下すようなものです。

このシンプルさが実は面白いんです！👩🏻‍💻
シンプルだけど、ここから複雑なAIの世界が始まっているというのが、なんともワクワクしますよね。まさにロマンですね。

パーセプトロンの基本構造と動作原理

パーセプトロンは、実はとてもシンプルな仕組みから成り立っています。
理解の鍵となるのは、次の3つの要素です。

1. 入力層（Input Layer）：
   ここには、データが入力されます。例えば、画像認識ならピクセルの色、音声認識なら音の波形などが入力されます。

2. 重み（Weights）：
   各入力に対して、「どれくらい重要か」を決めるための値です。入力が多ければ多いほど、これをどう設定するかが重要になります。

3. バイアス（Bias）：
   出力を調整するための値です。まるで調味料のように、全体のバランスを整えます。

これらが合わさって、パーセプトロンはデータに対する判断を行います。入力されたデータに対して、重みを掛け合わせて足し合わせ、その結果がバイアスを超えると「YES」、超えなければ「NO」といった判断を下すわけです。
これだけシンプルなのに、AIがどうやって判断しているのかが見えてきますね！

上記を図式化してみると下記のようになります。

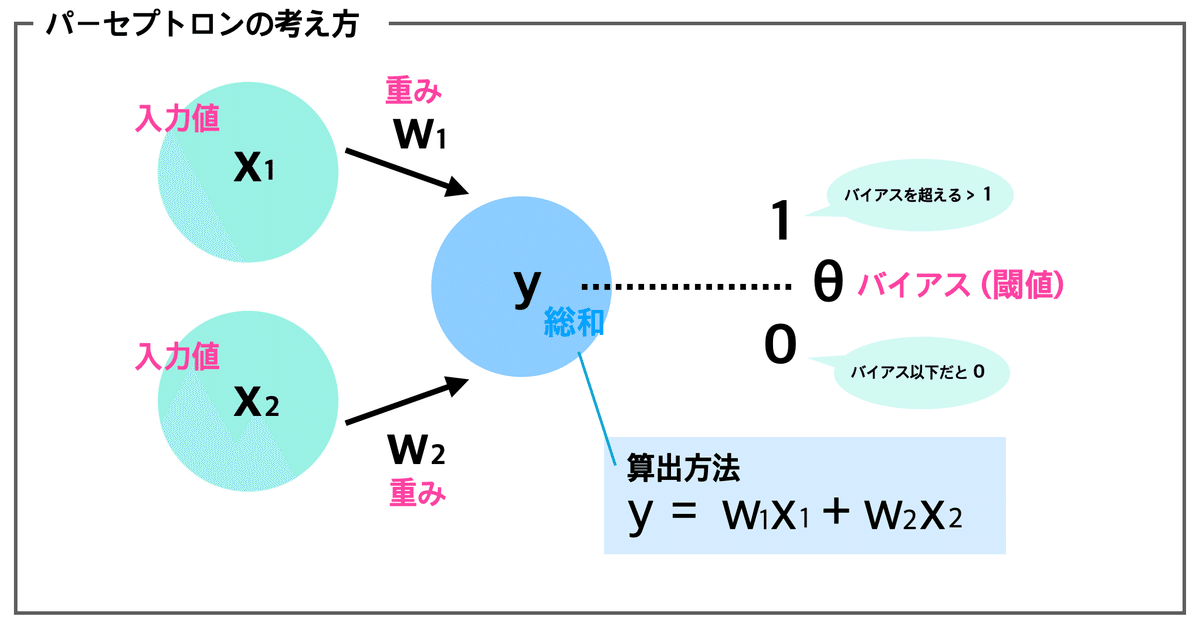
パーセプトロンで考える「単純な論理回路」について

次に、パーセプトロンがどのように論理回路を模倣できるかを考えてみましょう。

まず、論理回路とは、電気信号を使って「YES」か「NO」のような二択の答えを導き出す仕組みのことです。コンピュータの中では、この論理回路がたくさん組み合わさって、複雑な計算や判断を行っています。

パーセプトロンは、この論理回路の役割を果たすことができます。
具体的には、次のような基本的な論理ゲートを模倣することが可能です。

1. ANDゲート：
   すべての入力が「1」（電気が通る状態）の場合に「1」を出力します。
   たとえば、両手にスイッチがあり、両方を同時に押したときだけ電気が流れる仕組みです。

2. NANDゲート：すべての入力が「1」の場合に「0」を出力します。
   上記の例では、両手で押すと逆に電気が切れるというイメージです。

3. ORゲート：どれか一つでも「1」であれば「1」を出力します。
   片手でもスイッチを押せば電気が流れるという感じです。

例えば、家の電気スイッチを考えてみてください。両方のスイッチをオンにしないと電気がつかない場合はANDゲート、どちらか一つでもオンにすれば電気がつく場合はORゲートのような働きをしています。

実践！Pythonでのパーセプトロン実装

ここまでで、パーセプトロンの仕組みが少し見えてきたでしょうか？それでは、実際にPythonを使ってシンプルなANDゲートを実装してみましょう。

import numpy as np

# ANDゲートのパーセプトロンを定義
def AND(x1, x2):
    w = np.array([0.5, 0.5])  # 重み：両方の入力が等しく重要
    b = -0.7  # バイアス：しきい値を調整
    tmp = np.sum(w * np.array([x1, x2])) + b  # 入力×重みの総和にバイアスを加える
    if tmp > 0:  # 結果が0を超えたら
        return 1  # 出力1（YES）
    else:
        return 0  # それ以外は0（NO）

# ANDゲートをテスト
print(AND(0, 0))  # 期待出力: 0
print(AND(1, 0))  # 期待出力: 0
print(AND(0, 1))  # 期待出力: 0
print(AND(1, 1))  # 期待出力: 1

このコードでは、ANDゲートを実現するためのパーセプトロンを定義しています。
簡単に言うと、2つの入力（x1とx2）がどちらも「1」なら、出力も「1」になります。逆に、どちらかが「0」なら、出力も「0」になります。

重み（w）は、どの入力がどれだけ重要かを示し、バイアス（b）はその結果を調整する役割を果たします。このシンプルな例から、AIがどのようにして判断を下しているかの基礎が見えてきたのではないでしょうか？

最後のまとめ

いかがでしたでしょうか？
パーセプトロンの仕組みやその重要性について、この機会に少しでも興味を持ってもらえたら嬉しいです😇

次回の記事では、パーセプトロンを応用して、より複雑なAIの判断をどう実現するかを探っていきます。
今後のAIエンジニアとしてのスキルアップに繋がる内容をお届けしますので、ぜひお楽しみに！🐣

一緒に学びながら、AIエンジニアとしての夢に近づいていきましょう。
フォローして次回の記事もチェックしていただけると嬉しいです！
ここまで読んでくれてありがとうございました！