AtCoder Beginner Contest反省会 ~入緑編~

最近Pythonを勉強しはじめました。本を読み続けてページが進んでいくと充実感があるのですが、本を読んでるだけでは実は何も身についてないという厳しい現実に対して危機感があり、適度に課題を見つけて実践しようと努力しています。勉強が進んでないような焦りも感じますが、そうした中でしか得られない発見があると言い聞かせています。

「Wordleをやっててふと思いついた問題をPythonで解く」という記事は、そんな取り組みの1つです。この記事を書いたときに、noteの他のプログラミング記事をいろいろ読んでいると、AtCoderをやっている人が結構いて興味がわき、AtCoder Beginner Contest 266に初めて参加してみました。勉強になったので、自分のためという性質が強いですが、メモを書きます。今後参加したときもこの記事に追記していきます。上記、Wordleの記事で処理時間の長いプログラムを書きましたが、AtCoderをやっているうちに、一瞬で処理できるアルゴリズムが見つかるのではないかと思えてきて、探しています。

AtCoder Beginner Contest 266

時間内に正解したのはA、B、C、Eの4問でした。Aの時点で10分かかり、type(4/2)の結果が、<class 'float'>だったのがまず勉強になりました。Cまで正解したあと、Dの問題文を読んでおもしろい問題のように感じましたが、全く解き方の見当がつかず、あきらめてEに進むとEはすぐに解けました。Dが400点でEが500点なので、Eの方が難易度が高いのでしょうか？その後Fのコードを書いているときに制限時間となりました。G、Exはまだ問題も読んでいませんが、問題も理解できないかも知れません。

D - Snuke Panic (1D)

問題を読んでおもしろそうだと思い、なんとかしたかったですが、残念ながら全く解き方の見当がつきませんでした。解説を読むと動的計画法（Dynamic Programming, DP）と書いてあり、発想に驚きました。この問題を見るまで、でかい配列を作ってしまっていい（作らなくてもいいですが）という考えが、ぼくにはありませんでした。DPを知ると確かに簡単かもしれません。DPの他のパターンもいろいろ勉強しておきたいです。 2022-08-27

n = int(input())
t_max = 10**5
dp = [[-10**10]*5 for _ in range(t_max+1)]
sunuke = [[0]*5 for _ in range(t_max+1)]
t_last = 1
for _ in range(n):
    t, x, a = map(int, input().split())
    sunuke[t][x] = a
    if t > t_last:
        t_last = t
dp[0][0] = 0
for t in range(1,t_last+1):
    for x in range(5):
        dp[t][x] = dp[t-1][x]
        if x < 4 and dp[t-1][x+1] > dp[t][x]:
            dp[t][x] = dp[t-1][x+1]
        if x > 0 and dp[t-1][x-1] > dp[t][x]:
            dp[t][x] = dp[t-1][x-1]
        dp[t][x] += sunuke[t][x]
print(max(dp[t]))

追記1。問題Exを読んだところ、すぬけ君の出現領域がでかすぎて全領域メモリ確保は無理だったのでここに戻ってきました。最初にメモリ確保せず、すぬけくんの出現位置での情報だけで解いてみます。時間tに影響するのはt-3以降の影響があるものと、t-4以前の最大値という考え方で解きました。実行時間とメモリ使用量の最大値が242ms/103152KBから280ms/114388KBに増えたのが気になります（あれ？）が、全領域でDPやらなくても正常に動作しました。コードも上のよりスッキリしないですが、すぬけ君出現位置だけに注目して解ける感覚は得られました。問題Exに戻る。 2022-08-31

n = int(input())
sunuke = {}
bests = {}
ts = []
for _ in range(n):
    t, x, a = map(int, input().split())
    if x > t:
        continue
    sunuke[t] = (x, a)
    bests[t] = [0,0] # best at sunuke point and best so far
    ts.append(t)
best_so_far = 0
for i in range(len(ts)):
    j = i - 1
    max_effect = 0
    while j >= 0 and ts[j] > ts[i] - 4:
        if ts[i] - ts[j] >= sunuke[ts[j]][0] - sunuke[ts[i]][0] >= ts[j] - ts[i]:
            if bests[ts[j]][0] > max_effect:
                max_effect = bests[ts[j]][0]
        j -= 1
    if j >= 0 and bests[ts[j]][1] > max_effect:
        max_effect = bests[ts[j]][1]
    bests[ts[i]][0] = max_effect + sunuke[ts[i]][1]
    if bests[ts[i]][0] > best_so_far:
        best_so_far = bests[ts[i]][0]
    bests[ts[i]][1] = best_so_far
print(best_so_far)

F - Well-defined Path Queries on a Namori

xからyに行く単純パスが一意に定まるか？という問題。最初、xから同じ頂点を通らないルートを全探索して、2通り見つかった時点でNoとするコードを書いていましたが、当然それでは実行時間制限3秒に収まらずNGでした。グラフに関する数学的な知識を前提に解く必要があります。解説によるとN頂点N辺の連結なグラフのことを「なもりグラフ」といい、閉路が必ず1つのグラフになるそうです。なぜ閉路が1つになるのか考えてみました。3頂点では明らかに閉路1つです。N頂点で閉路0のグラフを作れたとすると、その枝の先の頂点と辺を除くことでN-1頂点で閉路0のグラフを作れることになり、3角形が閉路1つであることと矛盾します。閉路2つの場合については、枝があれば閉路0の場合と同じロジックで説明でき、枝がなければグラフは閉路2つだけとなり、連結であることに矛盾します。ということで、この問題の条件は「なもりグラフ」であることなので、1つの閉路とそこから木が生えた構造であり、同じ木に属する頂点同士は単純パスが一意に定まり、そうでなければ定まらないです。このような問題が出題されるのであれば、グラフ関連のこともいろいろ勉強しておきたいです。しかし「N頂点N辺の連結なグラフ」という前提条件が恣意的な感じもしてしまいますが、現実世界でよくあるのでしょうか？ 2022-08-28

Submission #34427826 - AtCoder Beginner Contest 266

グラフの問題を見直しているので久しぶりにやってみたら、難しかった。巡回路ノータッチで、サブツリーの部分を検出してやる。しかし処理速度が他の人より遅いのが気になるな。みんなどうやってんだろう？ぼくの提出は1826msから1506msになっただけ。この時から経験積んだからこなれたかもしれないけど、処理内容あまり変わってない？ 2022-12-17

N = int(input())
g = [set() for _ in range(N)]
for _ in range(N):
    u, v = map(int, input().split())
    g[u-1].add(v-1)
    g[v-1].add(u-1)
leaves = []
for i in range(N):
    if len(g[i]) == 1:
        leaves.append(i)
subtrees = {}
for leaf in leaves:
    cur = leaf
    v_subtree = set()
    while len(g[cur]) == 1:
        v_subtree.add(cur)
        next = g[cur].pop()
        if next in subtrees:
            v_subtree |= subtrees[next]
            subtrees.pop(next)
        g[next].remove(cur)
        cur = next
    v_subtree.add(cur)
    subtrees[cur] = v_subtree
sub = [-1]*N
for root, vs in subtrees.items():
    for v in vs:
        sub[v] = root
Q = int(input())
for _ in range(Q):
    x, y = map(int, input().split())
    if sub[x-1] != -1 and sub[x-1] == sub[y-1]:
        print('Yes')
    else:
        print('No')

G - Yet Another RGB Sequence

ついに、問題Gを解説を見ずに自力でACできました！比較的易しい問題ではありましたが、それでも今後の意識の変化につながる大きな一歩です。実は直前にABC267 Gで「挿入DP」を学んだ直後で、「数列に挿入していく」という見方が身についていたため、ぼくの頭が、この問題の解き方を思いつきやすい状態になっていた可能性はあります。DPかなと思わせてDPではありませんでしたが、ちゃんとひらめくことができました。しかもPythonでの提出が160くらいあって、処理速度が5位でした。高速化のノウハウが身についてきているのでしょうか？RGをKで置き換えると、まず、K、B、Rを並べたあとで、Rの後ろ以外にGを挿入すればよいことがわかります。最近、過去に参加したABCのGまでの問題を埋めていってたのですが、この問題が最後でした。 2022-12-16

M = 998244353
R, G, B, K = map(int, input().split())
R -= K
G -= K
N = max(K+B+R, K+B+G)
fact = [0]*(N+1)
invfact = [0]*(N+1)
fact[0] = 1
for i in range(1, N+1):
    fact[i] = fact[i-1] * i % M
invfact[N] = pow(fact[N], M-2, M)
for i in range(N-1, 0, -1):
    invfact[i] = invfact[i+1] * (i+1) % M
invfact[0] = 1
def choose(n, r):
    return fact[n] * invfact[r] * invfact[n-r] % M
ans = choose(K+B+R, K)
ans *= choose(B+R, B)
ans %= M
ans *= choose(K+B+G, G)
ans %= M
print(ans)

Ex - Snuke Panic (2D)

問題Dの2D版ということでおもしろそうです。問題読みましたが、問題Dで学んだDPが使えない。すぬけ君の出現範囲が問題Dでは5x10^5だったのに対し、Exでは10^9x10^9x10^9、全領域のメモリ確保できません。ですよねぇ。Dの解法でも気になってたポイントなので。ひとまず、問題Dに戻り、すぬけ君の位置だけの情報で解くプログラムを作ってからExに戻ってきます。この問題はそれだけでは済まないですが。一旦問題Dに戻る。 2022-08-31

問題Dから戻ってきました。別の解き方をしたことで、全領域メモリ確保せずにすぬけ君の位置だけに注目して解く考え方がわかりました。現在のすぬけ君の位置でのポイントの最大値を求めるには、その位置に到達しうるすぬけ君の位置全部の最大値+現在のすぬけ君の大きさを求めればよいです。問題Dでは出現範囲が5しかないので4秒以上前のすぬけ君全部の影響を受けることになり、4秒以上前の最大値を順次更新していけば解けましたが、問題Exは出現領域が広すぎて単純化できません。かと言って他のすぬけ君の位置全部に対して影響するかどうか調べているとそれだけでO(N^2)になってしまいます。解説を見ると2次元セグメントツリーという言葉が書いてありましたので、セグメントツリーについて勉強しました。なるほど、2分木を使うことで範囲の最大値の更新も取り出しもO(log(N))ででき、感動です。これを2次元にするというのは、イメージするのに苦労します。2次元でO(log(N)^2)で取り出せます。しかしメモリがN^2になってしまうなら結局解けねぇじゃねぇかという疑問が残ります。これ、データが入ってるところだけ確保することでN log(N)^2になるとの説明。確かに辞書を使えばできるので感動モノです。そこまで理解しても、すぬけ君の位置はtもあり、3次元領域なのでどうやって解けばいいかわからず、解説を見ました。(t, x, y) -> (a=t-x-y, b=t+x-y, y) と座標変換することで、aとbとyの値がすべて現在のすぬけ君以下のものの影響を受ける、と言い換えることができます。2次元セグメントツリーなどの高速アルゴリズムを知っている場合、この座標変換の方が問題を解くときの肝になりそうです。解説では不等式を変形していってaとbにたどり着いていますが、影響を受けるすぬけ君の位置と影響を受けない位置の境界において、t-x-yとt+x-yは一定となるため、意味的に考えてもしっくり来る変換です。でも機械的に式を変形して導けた方が良いようにも思います。実装するにあたり、解説のC++実装例を参考にしました。何日も気になって考えていたら疲れており、何かで行き詰まったときに参考にできるコードがないと、がんばるエネルギーがもう残ってないです。読み始めて気づいたんですが、これセグメントツリーじゃないです。まず、サイズがnで変だなと思いました。セグメントツリーならサイズ2nになるはず。あとx&-xというなぞのビット演算。フェニック木（Binary Indexed Tree、BIT）というものでした。x&-xは最下位ビットを取り出す処理になります。なぜそうなるかというと、x+(-x)が0になるということは、xと-xは最下位ビットが同じで、それより上位のビットは全部逆になるからですね。これを足したり引いたりしていますが原理がわかるとすごいです。作った人、定式化した時に興奮したんじゃないかなと感じました。自分でBITを実装するときは1から7くらいまでバイナリ表現で紙に書いてみるといつでも思い出せます。最初に作ったバージョンは制限時間の5秒を0.5秒くらいオーバーしました。もう改善できるところないよ、Pythonでは無理なのか？とあきらめかけましたが、defaultdictやsetdefaultを使っているところで、いらないノードを追加してしまっていることに気づき（！）if文やgetに変更して無事正解しました。BIT.set、BIT.prod、BIT2D.set、BIT2D.prodの中でsetdefaultやgetやif分岐を使い分けているところです。不十分な検討でむやみにdefaultdictとかsetdefaultとか使ってしまっていたことがわかり、勉強になりました。 2022-09-03

class BIT():
    def __init__(self, n):
        self.n = n
        self.maxima = {}
    def set(self, i, input):
        while i <= self.n:
            if input > self.maxima.setdefault(i, 0):
                self.maxima[i] = input
            i += i&-i
    def prod(self, i):
        res = 0
        while i > 0:
            if self.maxima.get(i, 0) > res:
                res = self.maxima[i]
            i -= i&-i
        return res
class BIT2D():
    def __init__(self, n, m):
        self.n = n
        self.m = m
        self.bits = {}
    def set(self, i, j, input):
        while i <= self.n:
            if i in self.bits:
                if input > self.bits[i].prod(j):
                    self.bits[i].set(j, input)
            else:
                self.bits[i] = BIT(self.m)
                self.bits[i].set(j, input)
            i += i&-i
    def prod(self, i, j):
        res = 0
        while i > 0:
            if i in self.bits:
                max1d = self.bits[i].prod(j)
                if max1d > res:
                    res = max1d
            i -= i&-i
        return res

n = int(input())
sunuke = []
pset = set()
qset = set()
for _ in range(n):
    t, x, y, a = map(int, input().split())
    if t >= x + y:
        p = t-x-y
        q = t+x-y
        sunuke.append((y, t, p, q, a))
        pset.add(p)
        qset.add(q)
pmap = {p:i+1 for i, p in enumerate(sorted(pset))}
qmap = {q:i+1 for i, q in enumerate(sorted(qset))}
sunuke.sort(key=lambda x: (x[0], x[1]))
pnum = len(pset)
qnum = len(qset)
bit2d = BIT2D(pnum, qnum)
for item in sunuke:
    p_compress = pmap[item[2]]
    q_compress = qmap[item[3]]
    max_pq = bit2d.prod(p_compress, q_compress)
    bit2d.set(p_compress, q_compress, max_pq + item[4])
print(bit2d.prod(pnum, qnum))

2次元セグメント木でもやっておきたいと気になっていたので、作ってみましたが、半分のテストケースで時間制限をクリアできません。厳しいですねぇ。いろいろ手を打ったけど、これ以上どこを改善できるのか？ただ、トライすることで、いろいろ気づきがあります。フェニック木は1から始まってたけど、このセグメント木は0からだなぁとか、無駄な処理いっぱいしてたなぁとか、デフォルト値は何かな？とか、更新するときに必ず更新するか、変更が入るときだけ更新するかみたいなのは問題によって変わるのかなぁとか。そういうことを考えているとライブラリーを使うってのも、何も考えずに適用できるわけではなく、問題に合わせて設定を変えたりする必要があって、なかなかむずかしいと認識しました。ACしないと意味ないですね。このコードでは、時間制限に引っかかってACできていないです。なんとかしたいけど、ここは一旦あきらめます。 2022-09-26

Submission #35186264 - AtCoder Beginner Contest 266

ABC283 Fをやっていて、初めてセグメントツリーで1問ACできた中で、改善点が見つかったので、ちょっと2次元セグメントツリーでのAC可能性でてきた？と思い修正してみました。再帰呼び出しをスタックに変更したり、無駄に子要素両方のmax値を計算し直していたのをやめたりしました。ていうか昔書いたコードってだめなところ見つかるもので、学習が進んでる証拠なのでいいですね。上にコピペしていたコードは問題があったので、コードは消して、提出リンクに変更しました。ていうか9月26日って始めてから1ヶ月のころです。それにしてはがんばっていて、時間間隔が変に感じます。が、確かに若干スピードアップしたものの、TLEx19がTLEx16になったに過ぎませんでした。正しく動いてそうなのは喜ばしいことですが。他のPythonでACしてる人の中で、フェニック木ではなくセグメントツリーを使っている人たちは、なぜか2次元部分を領域木というもので実装していそうです。領域木に秘密がありそうなので、領域木というものを別途学ぶ必要がありそうです。 2023-01-09

Submission #37906861 - AtCoder Beginner Contest 266

その後、ABC285 Fを通じて、さらにqueryの処理を改善し、またこの問題のTLE解消を期待しましたが、処理速度は速くなったものの、TLEの数は減りませんでした。 2023-01-16

Submission #38102815 - AtCoder Beginner Contest 266

AtCoder Beginner Contest 267

直前まで266のExをやってて頭が死んでる状態で、悩みましたが参加。A、B、Cまで解いて、Dがわかりませんでした。解説を見て驚愕。前回と同じでDPに持ち込む問題でしたがそのように見えてませんでした。まずは4問解くのが目標になりそうです。勉強になるのでおもしろいしやりたいけど、他の生活もあるので、続けてたらたぶん頭と体がもたないです。ある程度のレベルに達したらそんなことないのでしょうが。

B - Split?

問題がビットフラグで書かれていると影響受けます。 2022-09-04

Submission #34587252 - NEC Programming Contest 2022 (AtCoder Beginner Contest 267)

D - Index × A(Not Continuous ver.)

ABC 266 Dと同じでDPで解ける問題と解説で知りましたが、気づきませんでした。こういった問題をDPに持ち込める頭になる必要がありそうです。あと負数もありうるということのあつかいは要注意でした。0と比較して0を最大値として採用してしまってバグりました。 2022-09-04

n, m = map(int, input().split())
a = [0]
a.extend(list(map(int, input().split())))
dp = [[-10**12]*(m+1) for _ in range(n+1)]
dp[0][0] = 0
for i in range(1,n+1):
    dp[i][0] = 0
    for j in range(max(1, m-n+i), min(i+1, m+1)):
        dp[i][j] = max(dp[i-1][j], dp[i-1][j-1] + j * a[i])
print(dp[n][m])

E - Erasing Vertices 2

解説に、「「現時点でコストが最も低い頂点に対して操作を行う」を N回繰り返すのが最適であることがわかります」と書かれています。頂点を全部消さないといけないし、操作のたびに他の頂点に対する操作のコストはどんどん減っていくだけなので、言われてみると当たり前なのですが、これにすぐ気づけません。こういったことに短時間で気づけるにはどのように頭を使えばよいのでしょうか？とりあえず問題文にグラフと書かれているからと言ってなにか複雑な理論が必要だとは思い込まないようにします。そしてプライオリティーキューというものが使われていました。Pythonではheapqというライブラリになっています。ヒープ領域のヒープと全く関係なく、ヒープ木を使うアルゴリズムとのことです。最小のものをO(1)で取り出すことができますが、最小以外の要素に簡単に操作ができません。そこで、同じ頂点の以前登録した情報を残したまま、コストが小さくなった頂点の情報を、どんどんプライオリティーキューに追加していってます。そして頂点を消したかどうかは別のところで管理しておき、heapqからすでに消した頂点が取れたときは無視するという方法を取っています。コードだけ見ると「あれ？」と思いましたが理由があるんですね。理由があるにせよ、古くなった情報はキューから消さねば…という思い込みがあるので、これでいいんだ！というのは頭を刺激されました。 2022-09-04

import heapq
from collections import defaultdict
n, m = map(int, input().split())
a = tuple(map(int, input().split()))
removed = [False for _ in range(len(a))]
nexts = defaultdict(set)
costs = defaultdict(int)
for _ in range(m):
    u, v = map(int, input().split())
    iu = u-1
    iv = v-1
    nexts[iu].add(iv)
    nexts[iv].add(iu)
    costs[iu] += a[iv]
    costs[iv] += a[iu]
pq = [(item[1],item[0]) for item in costs.items()]
heapq.heapify(pq)
maxcost = 0
while pq:
    item = heapq.heappop(pq)
    id = item[1]
    if removed[id]:
        continue
    if item[0] > maxcost:
        maxcost = item[0]
    for next in nexts[id]:
        nexts[next].remove(id)
        costs[next] -= a[id]
        heapq.heappush(pq, (costs[next],next))
    nexts.pop(id)
    removed[id] = True
print(maxcost)

F - Exactly K Steps

この問題、むずかしいと思うのですが、自力で解くことができました。ABC281、ABC268に続いて問題Fを自力で解けたのは3回目です。それが3日以内に急に起きているので、力がついてきたのではないか？とうれしいです。ぼくはグラフ理論における、木の直径という概念を全く知りませんでしたが、この問題においてそれを求めれば良いと気づき、かつ、DFSを2回やれば求められることまで自力でたどり着けました。ABCに初めて参加した3ヶ月半前には考えられなかったようなことです。最長のパスをstem、それ以外をbranchと名付けて処理しました。Uのrootからの距離がK以上の場合は、K代上の先祖、Uがstemにあって最長パスの末端からの距離がK以上の場合は、K代子孫、Uがstemにあって最長パスの末端からの距離がK未満の場合は、なし、Uがbranchにあってbranch root（stem上のbranchの分かれ目）経由で末端までの距離がK以上の場合は、branch rootからK-(branch内距離)子孫、Uがbranchにあってbranch root（stem上のbranchの分かれ目）経由で末端までの距離がK未満の場合は、なし。と場合分けしました。すべての場合について、頂点が存在する場合はn世代上の先祖を求める問題に帰着し、nを2のべき乗に分解してアクセスできるようにしました。かなり複雑になりましたが、ここまで自分で導いてACできたことは、喜びたいと思います。提出時に最初ほとんどのケースでREとなってしまい、調査が難航し、バグ修正に何時間もかかってしまいました。コメントアウトなどして提出を繰り返してREの位置を特定して確認したところ、リストの要素に()でアクセスしており、not callableエラーが発生していたようでした。ローカルではよく起きるミスですが、AtCoderで起きてもエラーメッセージが見れないため、気づくのがかなり大変です。RE発生時のあるあるパターンとして、記憶しておかなければなりません。せっかくこのような難しい問題を自力で解けてうれしいのに、バグ調査に時間がかかって気分が萎え萎えになってしまいました。解説に良い方法が説明されていそうですが、今は読む気が起きません。しかしぼくのこのコード、長いししんどいです。いつかコンテスト時間内にこんなのも書けるときがくるのでしょうか？答えを求めるための処理の流れの方針を決めて紙一枚に書き出し、その方法で処理を組み立てるために必要なデータは何か？ということを抽出し、ようやくコードを書き始めました。苦労して完成したコードでACできるって達成感がありますね。 2022-12-13

import math
N = int(input())
nexts = [[] for _ in range(N)]
for _ in range(N-1):
    a, b = map(int, input().split())
    nexts[a-1].append(b-1)
    nexts[b-1].append(a-1)
root = N // 2 # arbitrary
longest = [root, 0]
used = [False]*N # need for undirected graph
stack = [(root, 0)]
while stack:
    cur, dist = stack.pop()
    used[cur] = True
    if dist > longest[1]:
        longest[0] = cur
        longest[1] = dist
    for next in nexts[cur]:
        if not used[next]:
            stack.append((next, dist+1))
root = longest[0] # reset root
dists = [-1]*N
# doubling [2^k][v]
max_double = math.floor(math.log2(N))
parents = [[-1]*N for _ in range(max_double + 1)]
longest = [root, 0]
stack = [(root, 0)]
# dfs again
while stack:
    cur, dist = stack.pop()
    dists[cur] = dist
    if dist > longest[1]:
        longest[0] = cur
        longest[1] = dist
    for next in nexts[cur]:
        if dists[next] != -1:
            # already accessed
            continue
        parents[0][next] = cur
        x = 0
        while x < max_double:
            if parents[x][parents[x][next]] == -1:
                break
            parents[x+1][next] = parents[x][parents[x][next]]
            x += 1
        stack.append((next, dist+1))
cur = longest[0] # this is longest end
used = [False]*N
branch_root = [-1]*N
while cur != root:
    used[cur] = True
    parent = parents[0][cur]
    for next in nexts[cur]:
        if used[next] or next == parent:
            continue
        stack = [next]
        while stack:
            branch_cur = stack.pop()
            # set branch root
            branch_root[branch_cur] = cur
            used[branch_cur] = True
            for branch_next in nexts[branch_cur]:
                if not used[branch_next]:
                    stack.append(branch_next)
    cur = parent
def ask_ancestor(v, step):
    i = 0
    cur = v
    while step:
        if step % 2 == 1:
            cur = parents[i][cur]
        step //= 2
        i += 1
    return cur
Q = int(input())
for _ in range(Q):
    u, k = map(int, input().split())
    u -= 1
    if dists[u] >= k:
        print(ask_ancestor(u, k)+1)
    else: # dists[u] < k
        if branch_root[u] == -1: # u on stem
            dist_from_end = longest[1] - dists[u]
            if dist_from_end >= k:
                print(ask_ancestor(longest[0], dist_from_end-k) + 1)
            else:
                print(-1)
        else: # u on branch
            local_root = branch_root[u]
            local_root_dist = dists[local_root]
            local_dist = dists[u] - local_root_dist
            # must < k
            dist_on_stem = k - local_dist
            dist_from_end = longest[1] - local_root_dist - dist_on_stem
            if dist_from_end >= 0:
                print(ask_ancestor(longest[0], dist_from_end)+1)
            else:
                print(-1)

G - Increasing K Times

問題Gを初めて自力で解くべく、DPだろうと思ったので、過去にやったDPの問題をすべてふりかえって、ヒントを抽出しました。インスピレーションを得たうえで、しばらくこの問題を考えてみましたが、結局なにもひらめかず、断念しました。解説によると「挿入DP」というようで、見たことがない全く新しい手法でした。それを使って苦労して解きましたが、提出した解答の処理時間は遅めで、TLEを回避するのにも苦労しました。でもなんか、むちゃくちゃ速い解答提出してる人いっぱいいるんですよね。どういう考え方で解いてるんでしょうか？問題Gって、ひらめけば一瞬で解ける問題が結構混じってるんでしょうか？ABC279 Gもそうでした。ABC279 Gは理解できましたが、この問題も理解したいです。 2022-12-15

from collections import defaultdict
M = 998244353
N, K = map(int, input().split())
acount = defaultdict(int)
for a in map(int, input().split()):
    acount[a] += 1

# https://atcoder.jp/contests/abc267/submissions/37291675
# 階乗やchooseの処理省略

alist = list(acount.items())
alist.sort(key=lambda x:x[0])
alen = len(alist)
dp = [0]*(K+2)
dp[0] = 1
total = 1 # gap number
shuffle = 1
for i, a_n in enumerate(alist):
    ii = i + 1 # ii is idx for a
    n = a_n[1]
    dp_new = [0]*(K+2)
    for j in range(min(K+2, total+1)):
        if not dp[j]:
            continue
        # j -> j + x <= K + 1
        for x in range(min(n+1, total-j+1, K+2-j)):
            if n-x > n+j-1:
                continue
            dp_new[j+x] += dp[j] * choose(total-j, x) * choose(n+j-1, n-x)
            dp_new[j+x] %= M
    dp = dp_new
    total += n
    shuffle *= fact[n]
    shuffle %= M
print(dp[K+1] * shuffle % M)

上記の通り、昨日提出したコードが遅いのが気になったので、やり直したところ、なんと、ぼくの提出が一気に最速となりました。速い人が特殊なことをやっていたわけではなく、同じく「挿入DP」ですが、同じ値の数字をまとめて挿入せず、1つずつ挿入しているだけのようです。あまりにもコードの様子が変わるので、すごいことしてるように見えてました。上のコードを提出した時は、まとめて挿入する方が自然だと感じてそのように実装したのですが、1つずつ挿入することによって複雑にならないし、むしろコードがむちゃくちゃシンプルになって速くなりました。Chooseを何度も計算するために、事前に階乗を計算しておくとか、必要なくなり、いいですね。シンプル・イズ・ベストです。やはりコードがシンプルなのは気持ちいいですね。ってまあ、場合によるのでしょうが。また、DPのリストをループの中で作り直していません。数字を挿入したときにAi<Ai+1となる箇所の個数は増えるだけなので、挿入したときにリストの中で影響を受けるインデックスは、より大きなインデックスとなります。より大きなインデックスにしか影響しないのであれば、大きい方から順に計算することで、DPのリストを直接更新することが可能となります。これは、ABC269 Gから学んだことです。DPの高速化では、非常に有効な方法ですね。早速使えてうれしいです。もう1つの高速化ポイントは、DPの状態遷移がi->i+1としたとき、iからi+1の状態を計算するのではなく、i+1の状態を、関係するiから引っ張ってきて計算しています。このことによって、i+1での新しい値が1回の足し算でも止まっています。これもポイントですね。ということで学んだノウハウが生きて、ぼくの提出が現在最速の132mとなりました。昨日の1666msから大幅に改善です。しかし「挿入DP」とはまたクレイジーです。この問題のような並べ替えの場合、左から確定していくと、残りの値を覚えておく必要があって破綻します。それを解決する秩序ある処理順が、小さい順に挿入していく方法だったというわけですね。 2022-12-16

from collections import defaultdict
M = 998244353
N, K = map(int, input().split())
acount = defaultdict(int)
for a in map(int, input().split()):
    acount[a] += 1
alist = list(acount.items())
alist.sort(key=lambda x:x[0])
alen = len(alist)
# init
dp = [0]*(K+2)
fact_a0num = 1
for i in range(2, alist[0][1]+1):
    fact_a0num = fact_a0num * i % M
dp[1] = fact_a0num
aida = alist[0][1] + 1
for a, n in alist[1:]:
    for acount in range(n):
        for k in range(min(aida+2, K+1), 0, -1):
            dp[k] = (dp[k] * (k+acount) + dp[k-1] * (aida-k+1-acount)) % M
        aida += 1
print(dp[K+1])

Ex - Odd Sum

数列の並び順は関係なく、どの数字を何個使うかだけ。ということに気づいてプログラミング脳になってきたか？いけるかも。とちょっと期待してランニングしながら頭の中で解き方を考えていたけど、どうしても計算量減らせず断念。解説を見てすげぇと思ったけど、高速フーリエ変換のしくみを思い出せないので一旦保留。高速フーリエ変換を勉強し直して戻ってきたいです。 2022-09-04

1ヶ月かかって高速フーリエ変換を勉強し、戻ってきました。1ヶ月と言ってもコンテストにたまに参加したりすると毎回毎回新しいことが出てきてそれを勉強しなければならず、高速フーリエ変換なんて勉強してるヒマがありませんでした。しかし解けてない問題はずっと気になるので、よしと思って一気にやった感じです。週末こんなのを理解しようとしてたら、久しぶりにとんでもなく頭が疲れたのを感じて、そのあとパワーナップしたら気持ち良すぎました。仕事でこの感覚を味わうことはできないのでいいですね。AtCoderに出てくるどのアルゴリズムを見てもクレイジーだと感じていますが、高速フーリエ変換は群を抜いてクレイジーだと思いました。1ヶ月前に読んで理解した解説を思い出しながら自力で動的計画法の実装をし、畳み込みの部分はmaspy氏のnumpyのfftを使った畳み込みを使い、サンプルに正解できました。サンプル問題で正解が出力された時は脳内物質が出てむちゃくちゃ興奮しました。たぶん、1ヶ月放置してた反動ですね。しかし提出したら実行エラーが発生しました。コードテストでModuleNotFoundError: No module named 'numpy'と出力されたので何かと思ったら、PyPyではnumpyが使えないけど、Pythonでは使えるということらしいです。今まで無意識にPyPy使ってました。PyPyは速いらしいので、numpyを取るかPyPyを取るかみたいな選択をせまられるんですね。 2022-10-02

ようやく正解できました。maspy氏のnumpyのfftを使った畳み込み、確かにconvolve2を使わないと不正解になっちゃいますね。最後ギリギリのところでの速度改善をしていて、大変でした。といっても今回numpyをはじめて使い、全く詳しくなかったので無駄に標準のlistを作ってからnumpyのarrayに変換したりしてたのをやめたら結構改善しました。combination計算のために階乗と階乗の逆元を事前に計算しておくところは、解説を参考にしましたが、逆元を1回しか計算しないのは効率的ですね。階乗計算のnはちゃんと一番多い数字の個数までしか計算しないようにしました。高速フーリエ変換をする時は、できるだけ係数のリストが小さくなるように、i*(iの個数)と、Mの小さい方の値までとしました。最後の最後でTLEがあと7つのテストケースとなったところで、入れた改善は、1から10まで順に計算するのではなく、i*(iの個数)が小さい順に計算するようにしたことです。畳み込みのたびにどんどんリストは大きくなるはずなので、できるだけ小さい状態を維持するには、係数リストが小さい順に計算したほうがよいはずです。この修正で十分速くなる保証はなかったですが、なんと、残りの7つのテストケースも間に合うことに成功しました。解説のC++コードが全く気にしていないところに気を使ってギリギリAC、やったぜ！って感じです。Pythonでの正解はぼくが11人目でしたが、ぼく以外全員PyPyでした。 2022-10-08

# fftコード省略

mod = 998244353
n, m = map(int, input().split())
from collections import Counter
counter = Counter(map(int, input().split()))
count_max = counter.most_common(1)[0][1]

# https://atcoder.jp/contests/abc267/submissions/35459588
# 階乗やchooseは省略

odd_prev = np.array([])
even_prev = np.array([])
is_first = True
counter_list = list(counter.items())
counter_list.sort(key=lambda x: (x[0]*x[1]))
for i, num in counter_list:
    coef_maxidx = min(i*num, m)
    odd_cur = np.zeros(coef_maxidx+1, dtype=np.int64)
    even_cur = np.zeros(coef_maxidx+1, dtype=np.int64)
    sum = 0
    even_cur[0] = 1
    is_even = False
    for n in range(1, num+1):
        sum += i # iをn個
        if sum > coef_maxidx:
            break
        if is_even:
            even_cur[sum] = choose(num, n) % mod
            is_even = False
        else:
            odd_cur[sum] = choose(num, n) % mod
            is_even = True
    if is_first:
        odd_prev = odd_cur
        even_prev = even_cur
        is_first = False
    else:
        new0 = convolve2(odd_prev, even_cur, mod) \
             + convolve2(even_prev, odd_cur, mod)
        new1 = convolve2(odd_prev, odd_cur, mod) \
             + convolve2(even_prev, even_cur, mod)
        odd_prev = new0[:m+1] if new0.size > m+1 else new0
        even_prev = new1[:m+1] if new1.size > m+1 else new1
if odd_prev.size >= m+1:
    print(odd_prev[m] % mod)
else:
    print(0)

AtCoder Beginner Contest 268

他にやることがあってリアルタイム参加はあきらめました。翌日、ワイン1杯飲んでましたが、バーチャル参加しました。時間内にはA、B、Cだけ解けました。Cが結構むずかしいと感じ、Cを解いた時点で35分くらいでした。それでも1時間以上残っているのでなんとか目標の4問を目指しましたが、D、Eがどちらもむずかしく、4問正解なりませんでした。過去問を6問やって解けるのも増えてきたかなと感じてましたがまだまだダメでした。D、Eの解説をみてやりましたが、実際むずかしかったです。

D - Unique Username

Tと一致しないことを短時間で判定できればよい。あとはこの条件に従ってユーザー名を生成したときにどれくらい作られるのか？ということが気になります。多すぎると処理が終わりません。まさにそれが解説に書かれていました。十分少ないとのこと。そして計算しなくてもプログラムを動かしてカウントしてみても良いと書かれていました。これは役に立つノウハウです。ぼくが、この問題を解けなかった原因は他にあり、そもそもどのようにユーザー名の候補を生成すればよいかで行き詰まってました。Xの文字数が3以上16以下ということで'_'を使う数に幅があり、それをどうあつかえばよいかわからず、行き詰まりました。不覚です。16文字ギリギリまで用意しておいて、右端の'_'列だけ捨てれば良いとのこと。これは気づけなかったのが悔しい。まあ'_'の数でループしても良いですが、頭疲れてます。そこまでわかれば、解けます。あとはユーザー名が3文字以上という条件を入れないと不正解になってしまうテストケースもあったので要注意でした。 2022-09-12

import sys
from itertools import permutations
from itertools import combinations
n, m = map(int, input().split())
ss = [input() for _ in range(n)]
ts = {input() for _ in range(m)}
s_all_len = len(''.join(ss))
us_split_point_num = 16 - s_all_len
for s_per in permutations(ss):
    for us_split_combi in combinations(range(us_split_point_num), n-1):
        us_lens = []
        id_cur = -1
        for id_temp in us_split_combi:
            us_lens.append(id_temp - id_cur)
            id_cur = id_temp
        res = ''
        for i in range(n-1):
            res += s_per[i]
            res += '_'*us_lens[i]
        res += s_per[n-1]
        if res not in ts and len(res) >= 3:
            print(res)
            sys.exit()
print(-1)

E - Chinese Restaurant (Three-Star Version)

頭の中にギザギザの不満度グラフがn個思い浮かんでいましたが、これをどう処理すればO(N^2)より小さくできるのかさっぱりわからず、公式解説を見ました。「いもす法」を使うと書かれていました。すべての場所で全データ処理しなくても、変化するところだけ覚えておいて、あとで走査すればO(N)で処理できるというものです。大事です。この問題のすごいところは、1次関数の次数ごとに「いもす法」を使うというところでした。クレイジーです。そこまでわかったとしても、同じ人の不満度を表す1次関数が範囲ごとに変化しギザギザになるので、それを正確に表現するのがむずかしく感じました。nが偶数だったら、nが奇数だったら、など考えました。実際最初バグっていて、1つだけ不正解が出て、整理し直してなんとか正解できました。今の実力で、時間内にこれを正解できる気はしません。むちゃくちゃ大変だと感じました。それにしても明らかにロジックに誤りがあるのに、1つを除いて正解になってしまったのは驚きました。この1つがなかったらバグを見つけられなかったと思うと、06_corner_03.txtはナイステストケースです。 2022-09-12

n = int(input())
ps = [p for p in map(int, input().split())]
imosu = [[0]*2 for _ in range(n)]
c = [[0]*2 for _ in range(n)]
for i, p in enumerate(ps):
    t = (p-i) % n
    if t < int(n/2):
        imosu[0][1] += -1
        imosu[0][0] += t
        imosu[t][1] += 2
        imosu[t][0] -= 2*t
        imosu[t+int((n-1)/2)+1][1] -= 2
        imosu[t+int((n-1)/2)+1][0] += (2*t + n)
    else:
        imosu[0][1] += 1
        imosu[0][0] += (-t + n)
        imosu[t-int(n/2)][1] -= 2
        imosu[t-int(n/2)][0] += (2*t - n)
        imosu[t][1] += 2
        imosu[t][0] -= 2*t
c[0][1] = imosu[0][1]
c[0][0] = imosu[0][0]
for x in range(1, n):
    c[x][1] = c[x-1][1] + imosu[x][1]
    c[x][0] = c[x-1][0] + imosu[x][0]
min = 10**11
for x in range(n):
    cur = x*c[x][1] + c[x][0]
    if cur < min:
        min = cur
print(min)

F - Best Concatenation

遡って解くぞシリーズ。この問題は自力で解くことができ、ABC281 Fに続いて2つ目の自力で解けた問題Fとなりました。ABC281は先週土曜日に開催され、今日は火曜日です。そして実はABC267 Fも、難しかったと思いますが、この問題のあとで自力で解けました。問題Fを初めて自力で解いてから、急に3日で3問、自力で解けたことになります。急に力がついたんでしょうか？うれしいです。この問題の考え方は、まず数字だけの文字列がXの前にあってもスコアになりませんから、全部まとめて後ろだなーと気づきました。よって、Xを含む文字列の順序だけ考えればよいとわかります。数字の区別は必要でしょうか？数字がそのままスコアになるので、区別せずに、全部足して考えればよいと気づけます。i番目とj番目の文字列のどちらを前に持ってこればよいでしょうか？i番目が前の場合と、j番目が前の場合、それぞれスコアを計算して大きくなる方の順序にすればよいです。Xの個数をnXi、nXjとし、数字の合計をFi、Fjとすると、スコアは、iが前の場合nXi*Fj、jが前の場合、nXj*Fiとなります。iを前にした方が良くなる、nXi*Fj > nXj*Fiを変形してFj/nXj > Fi/nXiということがわかり、F/nXでソートした順序が正解であることがわかります。最初に述べたように、nXが0のときは全部後ろでよいので、ソートのキーを最大値にしておきます。それぞれの文字列の中でもXの後ろに数字があればスコアになりますので、それも加えて答えを出力すればよいです。よし！解けるぞ！ 2022-12-13

N = int(input())
ans = 0
# X count, fugure sum
ss = [[0,0] for _ in range(N)]
for i in range(N):
    s = input()
    n_X = 0
    sum_fig = 0
    for c in s:
        if c == 'X':
            n_X += 1
        else:
            fig = int(c)
            ans += fig * n_X
            sum_fig += fig
    ss[i][0] = n_X
    ss[i][1] = sum_fig
ss.sort(key=lambda x:10**7 if x[0] == 0 else x[1]/x[0])
n_X = 0
for item in ss:
    ans += n_X * item[1]
    n_X += item[0]
print(ans)

G - Random Student ID

解説を読むだけの仕事になってしまってますが、時間を区切って解説を見ることにしないと体が持ちません。ていうかもう持ってないです。学籍番号の期待値を計算するということで、計算方法が全く検討つかなかったわけですが、解説によると、iさんの学籍番号の期待値を計算するには、jさんの名前がiさんの名前の接頭辞ならjさんは確実に前にいるので+1、iさんの名前がjさんの名前の接頭辞なら確実に後ろにいるので0、それ以外は1/2で計算すると。クレイジーです。期待値ってこうやって計算するんだということにまず驚き、そしてiさんとjさんの名前の何文字目かが異なる場合は前か後ろかの確率が1/2っていうのも驚きです。そして、トライ木（Trie）という構造を使うと、お互いに接頭辞になる人の人数を高速で数えられると書いてありましたので、素直に実装しました。ようやく提出したら、005.txtと015.txtだけ実行時エラー。同じ結果になってる人もいてなんだろうと思ったのですが、長い名前のテストケースを作って実行してみたら「RecursionError: maximum recursion depth exceeded」が発生し、原因がわかりました。深くなる再帰関数を使わないでおこうと思ってstackとかqueueを使ってたのですが、あきらめて、sys.setrecursionlimit(10**6)としました。これで無事正解です。ところで再帰回数が限界を超えたのはTrie.addです。別オブジェクトを作ってから呼んでるので、RecursionErrorが発生するまで、ぼくは再帰関数と認識していませんでした。Pythonってオブジェクトは引数のselfなんですよね。つまりオブジェクトを関数に渡して呼んでるだけなのでTrie.addを再帰的に呼び出していることになるという気づきが得られました。この問題では、有理数の答えをmod 998244353で出力するということで、これも厄介な話で、分子に分母の逆元（フェルマーの小定理により分母のm-2乘）をかけるとのこと。 2022-09-13

import sys
from collections import deque
sys.setrecursionlimit(10**6)
class Trie():
    def __init__(self, c='', parent=None):
        self.c = c
        self.parent = parent
        self.children = {}
        self.name = ''
        self.anc_num = 0
        self.desc_num = 0
        self.visited = False # for dfs
    def add(self, idx, name):
        if not self.c:
            if name[0] not in self.children:
                self.children[name[0]] = Trie(name[0], self)
            self.children[name[0]].add(0, name)
        elif idx == len(name) - 1:
            self.name = name
        else:
            if name[idx+1] not in self.children:
                self.children[name[idx+1]] = Trie(name[idx+1], self)
            self.children[name[idx+1]].add(idx+1, name)

m = 998244353
inv = pow(2, m-2, m)
n = int(input())
root = Trie()
ss = {} # s and answer
for i in range(n):
    s = input()
    ss[s] = 0
    root.add(0, s)
s = deque([])
s.append(root)
while s:
    trie = s.pop()
    if not trie.visited:
        trie.visited = True
        s.append(trie)
        for child in trie.children.values():
            child.anc_num = trie.anc_num
            if trie.name:
                child.anc_num += 1
            s.append(child)
    else:
        if trie.name:
            ss[trie.name] = ((1 + trie.anc_num - trie.desc_num + n) * inv) % m
        if trie.parent:
            trie.parent.desc_num += trie.desc_num
            if trie.name:
                trie.parent.desc_num += 1
for res in ss.values():
    print(res)

Ex - Taboo

Sを1文字目から順番に調べていき、Tが見つかったらその終端位置を覚える。その終端位置の中で一番手前のものを*に変える。という考え方でいけそうです。問題Gで覚えたばかりのトライ木で、最初に見つかるTの終端位置を見つけ、プライオリティキューに入れていけば一番手前をすぐに取り出せます。どう考えても計算量に無理がありますが、無駄な処理はいろいろ減らせるのでとりあえずやってみました。そして、不正解と時間切れになったのを確認して迷わず解説へ。公式解説のSuffix Arrayというクレイジーなアイデアに驚きつつ、SA-IS法がマジでわけがわからない（といいつつDNAとかの研究でも使うらしくむちゃくちゃ大事、O(N)でSuffix Arrayが作れるらしい）ので、別の方法を見ていると、エイホ–コラシック法（Aho-Corasick）というので解けるらしいと知りました。これはトライ木を発展させたものであり、大変わかりやすいです。Aho-Corasickは、トライ木の各ノードがSuffixが最も長く一致するノードへのリンクを持っている構造です。これを使うと、Sの文字を1文字進めるごとに最初からTと一致しているか調べ直さなくても、トライ木の途中から始まっているTもいっしょに調べることができてしまいます。Aho-Corasickは、トライ木のルートから幅優先で走査して生成できます。苦労してACしました。他の人よりメモリ使用量が多いのが解せません。 2022-09-18

import sys
sys.setrecursionlimit(10**6)
class Aho():
    def __init__(self, c=''):
        self.c = c # c is '' only when this is root
        self.children = {}
        self.is_word = False
        self.link = None
    def add(self, s, idx):
        if not self.c: # root
            if s[0] not in self.children:
                self.children[s[0]] = Aho(s[0])
            self.children[s[0]].add(s, 0)
        elif idx == len(s)-1:
            self.is_word = True
        else: # len(s) > 1
            if s[idx+1] not in self.children:
                self.children[s[idx+1]] = Aho(s[idx+1])
            self.children[s[idx+1]].add(s, idx+1)

from collections import deque
s = input()
n = int(input())
root = Aho()
for _ in range(n):
    t = input()
    root.add(t, 0)
q = deque([])
for rootchild in root.children.values():
    rootchild.link = root
    q.append(rootchild)
while q:
    node = q.popleft()
    cs = set(node.children)
    linkcand = node.link
    while cs:
        clist = list(cs)
        for c in clist:
            if c in linkcand.children:
                node.children[c].link = linkcand.children[c]
                if not node.children[c].is_word:
                    node.children[c].is_word = linkcand.children[c].is_word
                cs.remove(c)
            elif linkcand == root:
                node.children[c].link = root
                cs.remove(c)
        linkcand = linkcand.link
    q.extend(node.children.values())

i = 0
count = 0
aho = root
while True:
    if i == len(s):
        break
    if s[i] in aho.children:
        aho = aho.children[s[i]]
        if aho.is_word:
            count += 1
            aho = root
    else:
        while aho.c:
            aho = aho.link
            if s[i] in aho.children:
                aho = aho.children[s[i]]
                if aho.is_word:
                    count += 1
                    aho = root
                break
    i += 1
print(count)

AtCoder Beginner Contest 269

ABC268 Exが解けていなかったので、参加していません。その前のABC267 Exもまだ時間がかかりそうで、これ以上解けてない問題が増えるのは精神的にきついです。仕事もありつつ、Exの問題は1週間で理解できるレベルではないので、参加するエネルギーないです。その後日曜日にABC268 Exがなんとか解けたので、懲りずにABC269の問題を見てしまう。しんどいです。ググる回数が減るように、使った機能の復習はざっとした方が良さそうです。

B - Rectangle Detection

PyPyって文字列扱うのやたら遅いのでしょうか？なぜかPython勢もPyPyではなく、普通のPythonを使っている人が多く、その人達が実行速度上位でした。ムカついたので、C言語でテキトーに書いて2msにしました。1msは無理でしょうか。 2023-01-25

Submission #38308275 - UNICORN Programming Contest 2022(AtCoder Beginner Contest 269)

C - Submask

2022-09-19

n = int(input())
ans = [0]
while n:
    smallest = n & -n
    new = [i + smallest for i in ans]
    ans.extend(new)
    n -= smallest
for i in ans:
    print(i)

D - Do use hexagon grid

こういう連結成分の個数を出力する問題あるよなぁと思いながら、やったことがなかったです。ちょっと遠回りな感じもしますが、とりあえず隣同士のものを最初に見つけておいてから、幅優先でたどって全部のグリッドを見ればよいでしょうか？x, y, x-yの値が全部+-1の範囲にあるものが隣なので、そのように実装しました。最初bisectを使って-1から1の範囲を取り出していましたが、自分の環境では動くのに、AtCoderの環境では全テストケース実行エラーとなってしまいました。何かと思ったら、bisect.bisect()の引数のkeyを使っており、これはPython 3.10で追加されたので、AtCoderではまだ使えないようです。bisectなど使わず、座標の辞書を作ってもいけそうだったので、書き直して正解しました。 2022-09-19

from collections import defaultdict
from collections import deque
n = int(input())
nexts = {}
grids = []
c_dict = [defaultdict(set), defaultdict(set), defaultdict(set)]
for i in range(n):
    x, y = map(int, input().split())
    grids.append((x, y, x-y))
    c_dict[0][x].add(i)
    c_dict[1][y].add(i)
    c_dict[2][x-y].add(i)
for i in range(n):
    nextset = set()
    for dir in range(3):
        c = grids[i][dir]
        if dir == 0:
            nextset = c_dict[dir][c-1] | c_dict[dir][c] | c_dict[dir][c+1]
        else:
            nextset &= c_dict[dir][c-1] | c_dict[dir][c] | c_dict[dir][c+1]
    nextset.remove(i)
    nexts[i] = nextset
s = set(range(n))
count = 0
while s:
    count += 1
    q = deque([])
    x = s.pop()
    q.append(x)
    while q:
        cur = q.pop()
        for next in nexts[cur]:
            if next in s:
                s.remove(next)
                q.append(next)
print(count)

E - Last Rook

遡って解いていこうシリーズ。インタラクティブな問題は、Grundy数を使ってゲームに勝つ問題だったABC278 G以来、2回目です。今回は自力でいけました。が、i方向で絞り込んだ値をそのままj方向を調べるときにも使ってしまい、1ペナしてしまいました。1辺が1000なので、2^10より小さく、行列合計20回の2分探索で見つけることができ、質問回数の上限に設定されています。他の人より妙に遅いのが気になります。コードに違いがあるようには見えないのですが。 2022-12-10

N = int(input())
imin = 1
imax = N
while imin < imax:
    imid = (imin+imax) // 2
    print('?', imin, imid, 1, N, flush=True)
    T = int(input())
    if T < imid - imin + 1:
        imax = imid
    else:
        imin = imid + 1
# imin = imax
jmin = 1
jmax = N
while jmin < jmax:
    jmid = (jmin+jmax) // 2
    print('?', 1, N, jmin, jmid, flush=True)
    T = int(input())
    if T < jmid - jmin + 1:
        jmax = jmid
    else:
        jmin = jmid + 1
# jmin = jmax
print('!', imin, jmin)

F

めんどうなので、スキップ。 2022-12-11

G - Reversible Cards 2

問題Gを自力で解きたいと思ってやってますが、達成できず。これは相当難しかったです。そして非常に勉強になりました。いつものようにシンプルな問題ですが、公式解説にいろいろ書いてあって深いです。愚直に自分なりにDPをやるとこのようになりました。b-aの絶対値が同じものをまとめておき、負数の場合はマイナス回裏返すというように考えて、まとめて処理しています。この実装ではDPのリストをループ中で作り直しているので、b-aの絶対値が同じものに関しては、DPのリストの作り直し1回で済ませており、そこが高速化ポイントになっていると思ったのですが、これはTLEx8です。

Submission #37234142 - UNICORN Programming Contest 2022(AtCoder Beginner Contest 269)

解説の実装例を見ると、DPのリストを作り直していないんですよね。1つのリストを更新し続けて処理しています。これがものすごく不思議に見えました。ぼくは、カードの合計値のループの中で、裏返す回数のループを回していた上に、減るときをマイナス回にしてまとめて処理してたので、DPリストを作り直すしかないと思っていたんです。でも解説では、裏返す回数のループの内側で、カードの合計値のループを回し、かつ、裏返して合計値が増えるパターンのときはreverseした順序でループを回すことで、DPリストの作り直しが不要となっていました。リスト1つでも、処理順を工夫することで、排他的に実行しなければならないDPの更新処理が、互いに影響しないようにできるということです。それだけではなく、c増える操作をn回やる場合の処理を驚くべき方法で、高速化していました。自然数nをこのように分解していました。このループでnを分解したmの組み合わせで、1からnまでの自然数をすべて生成できることは、考えればわかります。n回裏返す処理が、log(N)回裏返す処理の組み合わせで表現できてしまいます。

x = 1
while n:
    m = min(n, x)
    # do something
    n -= m
    x *= 2

最終的なぼくのコードは、いろいろとがんばってこれで、1209msになりました。が、まだまだ速いコードが複数提出されています。中身を見ても何が違うんだかさっぱりわかりません。処理速度の違い、なぞなことが多いんですよねぇ。解説には|b-a|の種類が高々√M程度であることが、示されています。√M個の数字を小さい順にびっしり詰めると、1,2,3,4,…,√Mとなりますが、すべて加えると(√M(√M+1))/2です。負数も加えるとMを超えます。しかしΣb+Σa=Mであることから、Σ|b-a|は、明らかにM以下ですので、√M個 小さい順に詰めてもMを超えてしまうのであれば、|b-a|の種類は√M種類より小さくなければならないとわかります。つまり、Nが大きければb-aが同じものが大量に発生するので、今回のような高速化が可能です。入れ子ループのどちらを内側にするのかによって、自然数を分解した今回の高速化が可能になることや、ループの順序を工夫することでDPのリストは作り直す必要がなくなることなど、クレイジーな学びのある問題でした。あ、解説でreversed(range(l,r+1))というような書き方がされていましたが、range(r,l-1,-1)とした方が効率的なようです。 2022-12-12

import sys
input = sys.stdin.readline
from collections import defaultdict
N, M = map(int, input().split())
INF = N + 1
suma = 0
sub_count = defaultdict(int)
for _ in range(N):
    a, b = map(int, input().split())
    suma += a
    c = b - a
    if c != 0: # skip 0
        sub_count[c] += 1
dp = [INF]*(M+1)
dp[suma] = 0
l = r = suma
sub_ordered = list(sub_count.items())
sub_ordered.sort(key=lambda x:abs(x[0]*x[1]))
for sub, n in sub_ordered:
    x = 1
    while n:
        m = min(n, x) # m step at once
        for k in (range(r, l-1, -1) if sub > 0 else range(l, r+1)):
            if dp[k] == INF:
                continue
            k_ = k + sub * m
            dp[k_] = min(dp[k_], dp[k] + m)
        if sub > 0:
            r = r + sub * m
        else:
            l = l + sub * m
        n -= m
        x *= 2
for k in range(M+1):
    print(-1 if dp[k] == INF else dp[k])

Ex

理解するのきつそう。FFTはまた出てきたけどそれ以外のところ。 2022-09-19

AtCoder Beginner Contest 270

4問正解を目指して過去問などもやっていますが、基礎的なことを勉強していないせいで解説を読むたびに毎回度肝を抜かれ、ネットなどで調べて勉強しようとし、精神的にしんどいです。みんな基礎的な知識を身につけてやっているようで、どうやって身につけているんだろう？と調べてみると、蟻本に知りたかったことがいろいろ書かれていそうと気づきました。そこで今は蟻本を読み始めています。蟻本、問題に関連するアルゴリズムなど、気になったところを読めばいいと思ってましたが、全部読んだほうが良さそうです。いろいろと解けてない問題を抱えていてしんどいですが、そんなこと言ってたら永久に参加できないので今回のABCは参加しました。Cまでで1時間かかりました。Cのような、いかにも基本的な問題でも0から考えてる感じで時間がかかります。とはいえ、あと40分もあります。しかしDはまんまと引っかかって貪欲でいってしまい、正解できませんでした。むずかしいです。

C - Simple path

グラフの初級編のところを今蟻本で読んでるんですが、むずかしいです。この問題はいかにも基本って感じがしますが、ぼくにとっては0から考えてる感じでしんどいす。隣接リストを作り、そこから1を根とした木（各頂点の親と深さをメモ）を作り、xとyからLCA（Lowest Common Ancestor）まで親をたどっていきました。良いやり方なのかはわかりません。LCAに関連するアルゴリズムは今勉強したいと思っていることの1つで、この問題に関しては複雑なことをせずに解けましたが、気になっていることがいろいろあります。あと、この問題ではjoinで数値のlistを文字列化しようとしたときに失敗して手こずりました。strにしてからjoinしないといけないようです。' '.join([str(n) for n in [3,4,5]])。と思ったらリストを引数にアンパックして渡せるので、print(*l)でいいらしい。解説に書いてあったんですが、yを根にすればxから登っていくだけでよかったのか。なるほど！ 2022-09-24

from collections import defaultdict
from collections import deque
n, x, y = map(int, input().split())
par = [0 for _ in range(n+1)] # 0,1,2,..,n
depth = [-1 for _ in range(n+1)]
nexts = defaultdict(set)
for _ in range(n-1):
    u, v = map(int, input().split())
    nexts[u].add(v)
    nexts[v].add(u)
q = deque([])
q.append(1)
par[1] = 1 # root
depth[1] = 0
while q:
    cur = q.popleft()
    depth_cur = depth[cur]
    par_cur = par[cur]
    for c in nexts[cur]:
        if par[c] != 0:
            continue
        depth[c] = depth_cur + 1
        par[c] = cur
        q.append(c)
xline = [x]
yline = [y]
while True:
    if depth[x] > depth[y]:
        x = par[x]
        xline.append(x)
    else:
        y = par[y]
        yline.append(y)
    if x == y:
        yline.pop(-1)
        yline.reverse()
        xline.extend(yline)
        print(*xline)
        break

D - Stones

正解できませんでした。4問正解ならず。解説にこのように書いてあります。「「各手番で石を取れるだけ取る」という貪欲法で解くことはできません」反例を思いつかず、ひっかかりました。最初に提出したコードはこれです。半分のテストケースで不正解となりました。Sampleのテストケースでは気づけないようになっていたので厳しく、むずかしいです。

Submission #35132491 - TOYOTA MOTOR CORPORATION Programming Contest 2022(AtCoder Beginner Contest 270)

正しくはこのように動的計画法で解くとのことです。この感覚がまだ身についておらず、不思議な感じが抜けません。dp[n]はn個から始めて先手が取れる個数。その時後手の取れる個数はn - dp[n]。よって、先手が取れるのは、max(Ai + (n-Ai) - dp[n-Ai]) = max(n - dp[n-Ai])となる。0からnまで計算していく。 2022-09-24

n, k = map(int, input().split())
alist = []
for a in map(int, input().split()):
    alist.append(a)
dp = [0]*(n+1)
for i in range(n+1):
    for j in range(k):
        if alist[j] > i:
            break
        dp[i] = max(dp[i], i - dp[i-alist[j]])
print(dp[n])

E - Apple Baskets on Circle

これは特殊なことが不要で、愚直に回転数を重ねていくだけで正解できました。Dを飛ばしてこれを解いたほうが良かったようです。ただ、処理の流れを整理するのは苦労したので、短時間で整理できるように訓練が必要だと感じました。解説ではm回転したときの食べた個数をΣmin(a,m)で計算し、kになるところを2分探索していて勉強になりました。 2022-09-25

n, k = map(int, input().split())
alist = []
a_nonzero = []
for a in map(int, input().split()):
    alist.append(a)
    if a != 0:
        a_nonzero.append(a)
a_nonzero.sort()
i = 0
rot = 0
basket_num = len(a_nonzero)
a_prev = 0
while True:
    a = a_nonzero[i]
    if (a - a_prev) * basket_num >= k:
        rot += int(k / basket_num)
        amari = k % basket_num
        break
    k -= (a - a_prev) * basket_num # k > 0
    rot = a
    a_prev = a
    while a == a_nonzero[i]:
        i += 1
    basket_num = len(a_nonzero) - i
for i in range(len(alist)):
    alist[i] -= rot
    if alist[i] <= 0:
        alist[i] = 0
    elif amari:
        alist[i] -= 1
        amari -= 1
print(*alist)

復習なう。2分探索でやってみました。1回でACできて良かったですが、2分探索に慣れてないせいか、ループの終了条件がこれでいいのか？ちょっと悩んでしまいました。処理時間遅めです。 2023-01-05

Submission #37753153 - TOYOTA MOTOR CORPORATION Programming Contest 2022(AtCoder Beginner Contest 270)

F - Transportation

最小全域木の問題っぽい、ですが道路だけでなく、空港と港の建設によってつなぐこともできるため、解き方の見当がつきません。解説を読むと、空というノードを考え、空港建設のコストを、島と空をつなぐ道路のコストと考えればよいと書いてありました。港の場合は海をノードと捉えるのです。最初から空をノードにして最小全域木を作ってしまうと、必ず空港を建設するのが前提になってしまいますから、道路のみの場合と、空だけを追加する場合と、海だけを追加する場合と、空と海を両方追加する場合の4通りで最小全域木を計算し、一番コストが小さいものを回答すればよいです。またまた発想がクレイジー過ぎます。しかしこれを読むだけで、あー解けるなと思えるすごいトリックです。最小全域木はクラスカル法を使って解きます。新たに追加するエッジの両端ノードがすでに作られた木を通してつながっているかどうかは、Union-Findを使って判定します。このあたりは蟻本を見ながらUnionクラスとして実装しました。ノードの最大インデックス+1で初期化しているのでこれが無駄にでかくなると嫌ですが、まあ今後も使えると思います。この問題は道路だけですべての島をカバーできる前提ではないので、道路の最小全域木を求めても、答えになっていない場合が半分以上あるので注意が必要です。 2022-11-04

class Union():
    # 省略
n, m = map(int, input().split())
aircosts = [(x, i, n) for i, x in enumerate(map(int, input().split()))]
portcosts = [(y, i, n+1) for i, y in enumerate(map(int, input().split()))]
roads = []
road_cover = set()
for _ in range(m):
    a, b, z = map(int, input().split())
    roads.append((z, a-1, b-1))
    road_cover.add(a)
    road_cover.add(b)
# sky
es = roads + aircosts
es.sort(key=lambda x: x[0])
u = Union(n+1)
res = 0
for e in es:
    if not u.same_tree(e[1], e[2]):
        u.unite(e[1], e[2])
        res += e[0]
# sea
es = roads + portcosts
es.sort(key=lambda x: x[0])
u = Union(n+2)
cost_cur = 0
for e in es:
    if not u.same_tree(e[1], e[2]):
        u.unite(e[1], e[2])
        cost_cur += e[0]
if cost_cur < res:
    res = cost_cur
# sky and sea
es = roads + aircosts + portcosts
es.sort(key=lambda x: x[0])
u = Union(n+2)
cost_cur = 0
for e in es:
    if not u.same_tree(e[1], e[2]):
        u.unite(e[1], e[2])
        cost_cur += e[0]
if cost_cur < res:
    res = cost_cur
# when roads cover all islands
if len(road_cover) == n:
    roads.sort(key=lambda x: x[0])
    u = Union(n)
    cost_cur = 0
    for e in roads:
        if not u.same_tree(e[1], e[2]):
            u.unite(e[1], e[2])
            cost_cur += e[0]
    if cost_cur < res:
        res = cost_cur
print(res)

G - Sequence in mod P

遡ってGまで解くぞシリーズ！また新しい、あたおかな武器を手に入れてしまった。「Baby-step Giant-step」という。例によって自力で解こうとして、取りうる値は高々P個だからループするなぁ、そのループの中にGが含まれているのか？どうなのか？という問題だなぁ、一般項は求められるなぁ、などと考え行き詰まり、何か使える情報はないかと、ググって整数論の定理の記事などを苦しみながら読んでも、解決には結びつきませんでした。「Baby-step Giant-step」！いやぁクレイジーですね。理解して問題に適用するのに苦労しました。Wikipediaに書いてある例のように、Pがバカでかいときに、A^x≡B (mod P)となるxを求めるテクニックのようです。mを√P以上の数とします。x=im+jとすると、0<=i,j<mとすれば、xで0からP-1までカバーできます。A^j≡B(A^-m)^iと変形できます。A^jをj=0からmまで計算しておきます。A^-mを計算し、(A^-m)^iを、iを0からmまで変化させて計算します。先程計算したA^jの中のどれかと一致すれば、見つかったことになります。これまた、なんでこれで速くなってるの？とすごく不思議です。なぜか、ちょっと「半分全列挙」を思い出します。この離散対数問題を解く方法を見ると、A^-mを計算できていますが、この問題では逆関数m回の処理を計算していません。どう計算すればよいかも、よくわかりません。「Baby-step Giant-step」は、この問題のようなループする数列に対して適用できます。Baby-stepは数列を1歩ずつ進むことです。Giant-stepはm歩進むことです。Giant-stepでmずつm歩進むと、Baby-stepで0からm-1まで1歩ずつ進んだとき通った場所に、必ず当たるという性質を利用しています。√Pというのはどこから出てきたのか考えてみます。mは√Pでなくても、Babyでm歩、GiantでP/m歩歩けば同じ性質が得られます。BabyとGiantの歩数の合計であるm+P/mを最小化しようと思うと、m=√Pが導かれますので、そのような理由で√Pが採用されているのだと思います。この問題ではXi=S*A^i+B*(A^i-1)/(A-1)ですので、Giant-stepであるXmを直接計算することができます。あとはS=GやA=1やB=0のときを特別扱いする必要があって注意が必要でした。エグいです。最近の目標は、問題Gを自力で解くことになってますが、なかなか実現できません。 2022-12-09

import math
T = int(input())
for _ in range(T):
    P, A, B, S, G = map(int, input().split())
    if G == S:
        print(0)
        continue
    if A == 0:
        print(1 if G == B else -1)
        continue
    if A == 1:
        if B == 0:
            print(-1)
        else:
            print((G - S) * pow(B, P-2, P) % P)
        continue
    giant = math.ceil(P**0.5)
    cur = G
    babies = {cur:0}
    for i in range(1, giant):
        cur = (A * cur + B) % P
        babies[cur] = i # set biggest ok
    A_giant = pow(A, giant, P)
    A_giants = A_giant
    A_inv_1 = pow(A-1, P-2, P)
    for i in range(1, giant+1):
        val = (A_giants * S + (A_giants-1) * A_inv_1 * B) % P
        if val in babies:
            print(i*giant - babies[val])
            break
        A_giants *= A_giant
        A_giants %= P
    else:
        print(-1)

AtCoder Beginner Contest 271

Cでハマって過去最低の2問正解で終了し、無理かと思いましたが、入茶しました！。しかし、勉強続けてるのに点数が右肩下がりで納得いきません。

入茶しました！

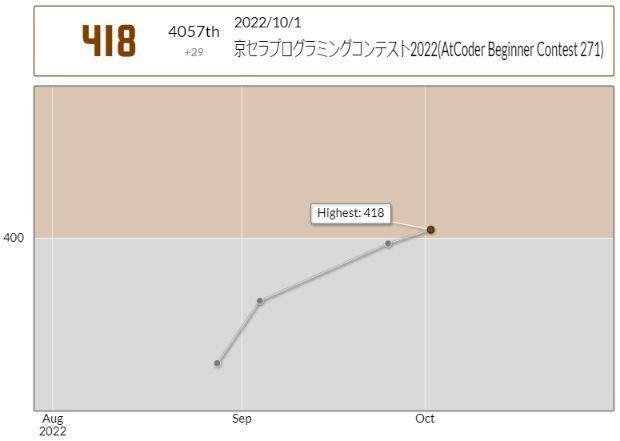
C - Manga

時間中、なんとか正解したいと粘りましたが解けず、ついに過去最低の2問正解で終わってしまいました。解説によるとx冊読めるかどうか簡単に計算できるので、2分探索すればよいと。問題がかなりシンプルに整理されて素晴らしいです。サンプル問題で「高橋君は同じ巻を 2 冊以上持っているかもしれません。」と書いてあり、いじわるだと思いましたが、高橋君が持ってる巻の数列が単調増加じゃないテストケースもありそうです。（たぶん。）だとするとユニークな巻を取り出すにはsetを使わなければならないので、問題を整理しきれてないから解けないんだとがんばっていたのに、これはさすがに悪意が強く、ひどい引っかけだと感じました。考えても意味がないことで時間を無駄にしたくないです。2分探索のコードは、はじめて書きましたが、自力で書いたら解説と同じになっていて良かったです。Pythonで、/で整数の割り算をするとfloatになってしまうことに気づいていたので、これまでint(n/2)というような書き方をしていましたが、切り捨て除算が別に用意されており、n//2と書けることを初めて学びました。 2022-10-01

n = int(input())
a_set = set(map(int, input().split()))
def can_read(x):
    global n
    i = len(set(range(1, x+1)) & a_set)
    return i + (n-i) // 2 >= x
l = 0
r = n+1
while r > l + 1:
    x = (l+r) // 2
    if can_read(x):
        l = x
    else:
        r = x
print(l)

上に書いた、高橋君が持っている巻の数列が単調増加じゃない引っかけテストケースを考慮し、ソートを1回入れたら最初の方針で正解できました。同じ巻を複数冊持っている場合はどんどん後ろに回し、持ってない巻があれば後ろから売って埋め合わせていくという割と愚直な方法です。1回目のsortを実行しないと、02_srnd_03、02_srnd_04、03_rnd_00、03_rnd_01、03_rnd_02、03_rnd_03のテストケースで不正解となりました。問題の条件を見れば単調増加じゃない可能性があることはわかるのですが、そこで引っかけても参加者にとって勉強にならないので、できればやめて欲しいです。笑。上の2分探索コードは892ms、このコードは179msで処理が終わりました。 2022-10-01

Submission #35328075 - KYOCERA Programming Contest 2022（AtCoder Beginner Contest 271）

復習なうです。今のところこのコンテストが唯一の2完ですが、この問題C確かにむずかしいですね。やっかいなので2完も納得です。もう一度やってみたらこうなりました。2分探索おもしろいけど、自然に考えたらこうなりますよね。 2023-01-06

N = int(input())
alist = list(map(int, input().split()))
alist.sort()
amari = 0
auniq = [alist[0]]
for i in range(1, N):
    if alist[i] == alist[i-1]:
        amari += 1
    else:
        auniq.append(alist[i])
auniq.extend([-1]*amari)
book = 1
i = 0
while i < N:
    if auniq[i] != book: # need to sell
        if N - i >= 2:
            N -= 2
            book += 1
        else: # not enough
            break
    else:
        book += 1
        i += 1
print(book-1)

D - Flip and Adjust

またもやわからん。解説に、できるかできないかを動的計画法でという説明があります。dpの範囲は100x10000。たしかに十分小さいです。そして、dpのマトリックスを作ってしまえば、逆向きにたどることで表か裏か決められるなぁ。クレイジーだなぁ。できる気がしないことをできてしまうマジック。ふぅ。 2022-10-01

import sys
n, s = map(int, input().split())
cards = []
for _ in range(n):
    a, b = map(int, input().split())
    cards.append((a,b))
dp = [[0]*(s+1) for _ in range(n+1)]
dp[0][0] = 1
for i in range(1, n+1):
    for j in range(s+1):
        x = dp[i-1][j-cards[i-1][0]] if j-cards[i-1][0] >= 0 else 0
        y = dp[i-1][j-cards[i-1][1]] if j-cards[i-1][1] >= 0 else 0
        dp[i][j] = x | y
if dp[n][s] == 0:
    print('No')
    sys.exit()
else:
    print('Yes')
i = n
res = ''
while True:
    if i == 0:
        break
    if dp[i-1][s-cards[i-1][0]] == 1:
        s -= cards[i-1][0]
        res += 'H'
    else:
        s -= cards[i-1][1]
        res += 'T'
    i -= 1
print(res[::-1])

E - Subsequence Path

古いのを遡ってやり始めています。考えすぎてわからなかったのですが、コードを見ての通り、かなり簡単な処理で解ける問題です。くやしいです。数列Eを順番に処理して、その道を使ったときに次の都市に低いコストでたどり着ければ距離を更新する。それだけです。しかも同じリスト上で更新していくだけでOKです。こんなにシンプルなのに考え込んでしまってわからないってくやしいなぁ。長い文字列が入力されるので、input = sys.stdin.readlineでの高速化が有効に働く問題です。 2022-12-03

import sys
input = sys.stdin.readline
N, M, K = map(int, input().split())
A = [0]
B = [0]
C = [0]
for _ in range(M):
    a, b, c = map(int, input().split())
    A.append(a)
    B.append(b)
    C.append(c)
costs = [10**15]*(N+1)
costs[1] = 0
for e in map(int, input().split()):
    cnext = C[e] + costs[A[e]]
    costs[B[e]] = min(cnext, costs[B[e]])
print(-1 if costs[N]==10**15 else costs[N])

F - XOR on Grid Path

「半分全列挙」というらしいですが、そこまでは、なぜか自力でたどり着けました。(1,1)から対角線上にある、i+j=N+1のマスまでの通り道の組み合わせは、最大2^20通りなので100万程度になることがわかります。ということは、そのまま(N,N)まで行く組み合わせはその2乗で1兆ということになり、すべて計算できません。しかし(N,N)から逆に進んで来て対角線にたどり着く場合はまた100万程度の計算で済み、出会ったところで比べれば良いのではないでしょうか？問題のマス目を見ていて自然に思いついたのですが、1兆通り計算しなければならないところを、√1兆=100万の計算で済んでしまうなんて、なんでそんなことが可能なのか？これまた化かされたような気分です。気づけたにも関わらず、あれ？なんでこんなに計算量減るんだ？と不思議でした。とはいえ、それがわかったあとの実装も結構大変でした。コードを見るとなんかサラッと書いてるように見えますが、ループを回すときのインデックスの値をちゃんと決めるのに苦労してました。こういったループ中の変数の値の整理を短時間で行うのは、まだまだ苦手だなぁと思います。XORが0になるのは、同じ値同士の場合だけです。なので(1,1)から来た値と(N,N)から来た値が一致している組み合わせ数を調べればよいです。そこはCounterを使って計算しました。pythonのCounter、めっちゃ便利ですね。 2022-12-04

N = int(input())
alist = []
for _ in range(N):
    alist.append(list(map(int, input().split())))
# print(alist)
res1 = [[[] for _ in range(N)] for _ in range(N)]
res1[0][0].append(alist[0][0])
for i in range(1, N):
    j = i-1
    while j >= 0:
        k = i-1-j # j+k = i-1
        res1[j+1][k].extend([val^alist[j+1][k] for val in res1[j][k]])
        res1[j][k+1].extend([val^alist[j][k+1] for val in res1[j][k]])
        j -= 1
res2 = [[[] for _ in range(N)] for _ in range(N)]
res2[N-1][N-1].append(alist[N-1][N-1])
for i in range(N-1, 0, -1):
    j = i
    while j <= N-1:
        k = i+N-1-j
        if i == 1:
            res2[j-1][k].extend(res2[j][k])
            res2[j][k-1].extend(res2[j][k])
        else:
            res2[j-1][k].extend([val^alist[j-1][k] for val in res2[j][k]])
            res2[j][k-1].extend([val^alist[j][k-1] for val in res2[j][k]])
        j += 1
from collections import Counter
ans = 0
for i in range(N):
    j = N-1-i
    count1 = Counter(res1[i][j])
    count2 = Counter(res2[i][j])
    for n in count1:
        if n in count2:
            ans += count1[n]*count2[n]
print(ans)

G - Access Counter

勉強になるので、参加し始めてからのABCの問題Gまでを、遡ってやっています。問題Gを自力で解けるようになりたいですが、まだまだです。半分くらいは自力で進むのですが、最後の1手がわからないというような感覚があります。その1手に毎回驚いて刺激を受けるのでやめられません。この問題は、i時にアクセスが発生してから次にj時にアクセスが発生する確率が無限級数で計算でき、24個の状態が次にどこに遷移するかの確率が計算できるということまで自力でたどり着けました。1回目は24通り計算すればいいです。2回目は24x24通り計算すれば良い。これくらいなら計算できるなぁということまでわかりましたが、Nの最大値が10^18と書いてあるのを見て行き詰まりました。1ステップずつ進む方法しか思いつかなかったからです。これだけNがでかいと、毎回24x24通り計算するのは無理です。と、ここまで自分でたどり着けるだけでもずいぶん成長した気がします。解説を見てやられたと思いました。「繰り返し二乗法」という名前がついているようです。そういえば、べき乗の計算の中身がこういうやり方で、なるほどと思ったことがあるのですが、この問題は複雑だったので、思いつけませんでした。気づけるようになりたいものです。 2022-12-08

MOD = 998244353
inv100 = pow(100, MOD-2, MOD)
N, X, Y = map(int, input().split())
# X:T高橋, Y:A青木
S = input()
p = [(X if c=='T' else Y)*inv100%MOD for c in S] # access
q = [(100-X if c=='T' else 100-Y)*inv100%MOD for c in S] # noaccess
rate_next = [0]*(24*24)
rates = [rate_next]
for i in range(24): # prev access is i
    noaccess_sum = 1
    for j in range(1,25):
        t_next = (i + j) % 24
        ij = i * 24 + t_next
        rate_next[ij] = noaccess_sum * p[t_next] % MOD
        noaccess_sum = noaccess_sum * q[t_next] % MOD
infx = pow(1-noaccess_sum, MOD-2, MOD)
for i in range(24*24):
    rate_next[i] = rate_next[i] * infx % MOD
def multiply(l, r):
    ret = [0]*(24*24)
    for i in range(24):
        for j in range(24):
            idx = i * 24 + j
            for k in range(24):
                ret[idx] = (ret[idx] + l[i*24+k]*r[k*24+j]) % MOD
    return ret
count = 1
N_half = N // 2
while count <= N_half:
    rates.append(multiply(rates[-1], rates[-1]))
    count *= 2
digit = 0
first = True
while N:
    if N % 2 == 1:
        N -= 1
        if first:
            total_multiply = rates[digit]
            first = False
        else:
            total_multiply = multiply(total_multiply, rates[digit])
    N //= 2
    digit += 1
ans = 0
for i, c in enumerate(S):
    if c == 'A':
        ans = (ans + total_multiply[24*23+i]) % MOD
print(ans)

AtCoder Beginner Contest 272

前回に続き、問題Cで罠にハマってしまい5回も不正解を提出して、時間をロス。Cはなんとか解けましたが、Dは間に合わず、3問正解でした。前回2問正解で入茶したのに、早速脱落しかけています。直前までABC267 Ex Odd Sumをがんばっていて、なんとか正解できた直後の参加でした。解けない問題が積み上がっていると疲れますね。完全消化してから次のコンテストに臨めるようになりたいものですが、今の実力では無理です。いずれできるようになるのでしょうか？

C - Max Even

大きい順に3つの数字を選べば、その中の2つの和に必ず偶数が現れるなぁ、と思い、その値を回答すれば良いと思いこんでしまいました。実際には2番目と3番目の和より、1番目と4番目の和の方が大きい可能性があります。このことになかなか気づけず、なんとか正解したときには1時間以上経っていました。つらい。偶数の上位2つの和と奇数の上位2つの和を比較して大きい方を回答すればよかったのですね。それならシンプルでわかりやすいです。でも思いこんでしまうと抜け出せないなぁ。 2022-10-08

リベンジ。今となってはこうとしか思えないな。 2023-01-06

import sys
input = sys.stdin.readline
N = int(input())
even = []
odd = []
for a in map(int, input().split()):
    if a % 2 == 0:
        even.append(a)
    else:
        odd.append(a)
ans = [-1]
if len(even) >= 2:
    even.sort()
    ans.append(even[-1]+even[-2])
if len(odd) >= 2:
    odd.sort()
    ans.append(odd[-1]+odd[-2])
print(max(ans))

D - Root M Leaper

間に合わなかったけど、Cでハマらずに十分時間が取れたら正解できたかもなぁと思っています。 2022-10-08

from collections import deque
n, m = map(int, input().split())
import math
move = set()
for i in range(m):
    j2 = m - i**2
    if j2 < 0:
        break
    root_j2 = int(math.sqrt(j2))
    if root_j2**2 == j2:
        move.add((i,root_j2))
        move.add((i,-root_j2))
        move.add((-i,root_j2))
        move.add((-i,-root_j2))
        move.add((root_j2,i))
        move.add((-root_j2,i))
        move.add((root_j2,-i))
        move.add((-root_j2,-i))
grid = [[-1]*n for _ in range(n)]
q = deque([])
grid[0][0] = 0
q.append((0, 0))
while q:
    x, y = q.popleft()
    for delta in move:
        x_next = x + delta[0]
        y_next = y + delta[1]
        if 0 <= x_next < n and 0 <= y_next < n:
            if grid[x_next][y_next] == -1:
                grid[x_next][y_next] = grid[x][y] + 1
                q.append((x_next, y_next))
for i in range(n):
    print(*grid[i])

E - Add and Mex

これは無理だろ、M回の操作すらできないよ。と思って解説を見たら0からNまでの範囲内には、調和級数により、O(N log(N))しか入ってこないのだとか。調和級数なんて普段考えることないと、衝撃を受けますね。その情報を元にやってみると正解できました。考え方はむちゃくちゃ普通ですが、いけるという判断をするのがむずかしいですね。 2022-10-08

import math
n, m = map(int, input().split())
alist = list(map(int, input().split()))
val_list = [set() for _ in range(m+1)]
for i, a in enumerate(alist):
    i += 1
    if a > n:
        continue
    l = max(1, math.ceil(-(a/i)))
    r = min(m, math.floor((n-a)/i))
    for j in range(l, r+1):
        val_list[j].add(a + i*j)
for i in range(1, m+1):
    for j in range(n+1):
        if j in val_list[i]:
            continue
        print(j)
        break

F - Two Strings

ABCに参加するようになってから、Suffix Array（接尾辞配列）という言葉に何度かめぐりあっています。Suffix Arrayという概念に最初に触れた時は「マジかよ」と思いました。そこソートすんのかよ！と。しかもSA-ISという方法を使うとO(N)で計算できるようです。エグすぎます。ぼくは問題を解くときに、必要なアルゴリズムを一応理解して、自分なりに実装して解こうと試みるのが、基本姿勢としてあります。SA-ISも理解しようとはしましたが、こればかりは意味不明だったため、処理の流れを追ったところで自分で実装するエネルギーなどなく、「Suffix Arrayで解けます」と書かれている問題には、なかなか手を付けられずにいました。蟻本ではSA-ISの実装は説明されていません。ダブリングの実装が書かれています。しかしダブリングでは間に合わない問題が出題されてるっぽいですよね。もうSA-ISはブラックボックスとして使うしかないと腹をくくりました。「SA-IS Python」でググるとyaketake08さんの実装がヒットしますのでこれを使わせていただきました。で、普通に解けました。今後は苦手意識を持たずにSA-ISを使えるようになっていきたいです。解説では、SS、'a'をN回連続、TT、'z'をN回連続をつなげた文字列Xを考え、これのSuffix Arrayを構築すればよいと書いてありました。しかし、a-zだけを使うことにこだわらなければ、SS`TT{という文字列Xでいけると思いましたので、そのように実装しました。SA-ISを使う問題が解けたのは気持ちいいです。文字列Xを作ってSuffix Array、かなりおもしろい解き方だと思いました。 2022-11-04

# https://tjkendev.github.io/procon-library/python/string/sa_sa-is.html
# SA-ISコード省略

n = int(input())
s = input()
t = input()
x = s + s + chr(ord('a')-1) + t + t + chr(ord('z')+1)
res = 0
count_t = 0
for i in sais(x):
    if 2*n+1 <= i <= 3*n:
        count_t += 1
    elif 0 <= i <= n-1:
        res += (n-count_t)
print(res)

蟻本を読んで作ったダブリングバージョンも載せておきます。ACx9、TLEx63でした。だめだこりゃ。SA-ISがないとやってられねぇ。 2022-11-04

def sa_doubling(x):
    n = len(x)
    sa = [0]*(n+1)
    rank = [0]*(n+1)
    tmp = [0]*(n+1)
    def compare_sa(i, j, k):
        if rank[i] != rank[j]:
            return rank[i] < rank[j]
        else:
            ri = rank[i+k] if i+k <= n else -1
            rj = rank[j+k] if j+k <= n else -1
            return ri < rj
    for i in range(n+1):
        sa[i] = i
        rank[i] = ord(x[i]) if i < n else -1
    k = 1
    while True:
        if k > n:
            break
        sa.sort(key=lambda x: (rank[x], rank[x+k] if (x+k) <= n else -1))
        tmp[0] = 0
        for i in range(1, n+1):
            tmp[sa[i]] = tmp[sa[i-1]] \
            + (1 if compare_sa(sa[i-1], sa[i], k) else 0)
        for i in range(n+1):
            rank[i] = tmp[i]
        k *= 2
    return sa

n = int(input())
s = input()
t = input()
x = s + s + chr(ord('a')-1) + t + t + chr(ord('z')+1)
res = 0
count_t = 0
for i in sa_doubling(x):
    if 2*n+1 <= i <= 3*n:
        count_t += 1
    elif 0 <= i <= n-1:
        res += (n-count_t)
print(res)

G - Yet Another mod M

自力でたどり着けたのは、Mは素数と4だけで良いな、というところまででした。解説を見ると、「確率的にほぼ正解が出る」という解法が書かれており、みんなそれを使って高速なプログラムを書いていることに驚きました。一般的なやり方なのでしょうね。もう一方の解法は確実性のある方法だったのでこちらの方法で解くことにします。過半数がmod Mで一致するという条件から、もしもMが存在するなら、隣同士の数字の差の約数の中に含まれることがわかります。これ、気づけませんでした。なるほどです。確かに過半数の中に、必ず隣あうものが存在するはずです。3以上の素数と4のみでよいということまでは、わかっているので、見つかった素数で全探索しています。速度は出ませんが、これでACできました。この問題で、素因数分解のプログラムも勉強できたので、良かったです。 2022-12-01

import sys
from collections import defaultdict
N = int(input())
half = N // 2 + 1
alist = list(map(int, input().split()))
# return set of prime or 4 except for 2
def prime_factorization(n):
    res = set()
    count2 = 0
    while n % 2 == 0:
        count2 += 1
        n //= 2
    if count2 >= 2:
        res.add(4)
    a = 3
    while a*a <= n:
        while n % a == 0:
            res.add(a)
            n //= a
        a += 1
    if n != 1:
        res.add(n)
    return res
# return True if found
def checkall(p):
    counter = defaultdict(int)
    countmax = 0
    for i in range(N):
        a = alist[i]
        x = a % p
        counter[x] += 1
        if counter[x] == half:
            return True
        if counter[x] > countmax:
            countmax = counter[x]
        if countmax + N - 1 - i < half:
            return False
    return False
checked = set()
for i in range(N):
    diff = abs(alist[i]-alist[0 if i == N-1 else i+1])
    cands = prime_factorization(diff)
    for p in (cands-checked):
        if checkall(p):
            print(p)
            sys.exit()
    checked |= cands
print(-1)

AtCoder Beginner Contest 273

京都に旅行してたので不参加でした。

久世橋から桂川

グリルはせがわ

グリルはせがわのAミックス

この回も2022年末から2023年始にかけて問題Gまでやりました。 2023-01-03

D - LRUD Instructions

書き方をミスるだけでわかりにくいコードになってしまいそうな問題です。整理してわかりやすく書ければ良いと思いました。境界部分は全部壁と思えば良いので、defaultdictのdefault値をlambda関数で渡してdefaultdict(lambda: [0,W+1])としているあたりや、1方向の移動後の位置を、壁の前と壁がない場合に到達する位置の近い方、というように表現したことでわかりやすくなったと思います。 2022-12-30

import sys
input = sys.stdin.readline
from collections import defaultdict
import bisect
H, W, ti, tj = map(int, input().split())
N = int(input())
blocks_hori = defaultdict(lambda: [0,W+1])
blocks_vert = defaultdict(lambda: [0,H+1])
for _ in range(N):
    i, j = map(int, input().split())
    blocks_hori[i].append(j)
    blocks_vert[j].append(i)
for i in blocks_hori:
    blocks_hori[i].sort()
for j in blocks_vert:
    blocks_vert[j].sort()
Q = int(input())
ans = []
for _ in range(Q):
    d, c = input().split()
    c = int(c)
    if d == 'L':
        blocks = blocks_hori[ti] if ti in blocks_hori else [0,W+1]
        idx = bisect.bisect(blocks, tj)
        tj = max(tj - c, blocks[idx-1] + 1)
    elif d == 'R':
        blocks = blocks_hori[ti] if ti in blocks_hori else [0,W+1]
        idx = bisect.bisect(blocks, tj)
        tj = min(tj + c, blocks[idx] - 1)
    elif d == 'U':
        blocks = blocks_vert[tj] if tj in blocks_vert else [0,H+1]
        idx = bisect.bisect(blocks, ti)
        ti = max(ti - c, blocks[idx-1] + 1)
    elif d == 'D':
        blocks = blocks_vert[tj] if tj in blocks_vert else [0,H+1]
        idx = bisect.bisect(blocks, ti)
        ti = min(ti + c, blocks[idx] - 1)
    ans.append('{} {}'.format(ti, tj))
print(*ans, sep='\n')

E - Notebook

問題文を素直に読むと、SAVEで整数列Aを丸ごとノートにコピーしたり、LOADでノートからAに丸ごとコピーしてきたりと、膨大な処理が必要になるように読めますが、Aを整数のツリーで管理すると、SAVEはツリーNodeにタグをつけることに、LOADはツリーNodeにポインタを移動することに対応し、膨大な操作は不要となります。問題の読み替えができるかどうかにかかっている、おもしろい問題です。 2022-12-30

import sys
input = sys.stdin.readline
class Node():
    def __init__(self, c, p):
        self.p = p # parent
        self.c = c
        self.children = {} # c -> Node
    def add(self, c): # return added Node
        if c not in self.children:
            self.children[c] = Node(c, self)
        return self.children[c]
note = {} # int -> Node
Q = int(input())
cur = ROOT = Node('', None) # root
ans = []
for _ in range(Q):
    q = input().split()
    if q[0] == 'ADD':
        cur = cur.add(int(q[1]))
    elif q[0] == 'DELETE':
        if cur != ROOT:
            cur = cur.p
    elif q[0] == 'SAVE':
        note[int(q[1])] = cur
    elif q[0] == 'LOAD':
        if int(q[1]) in note:
            cur = note[int(q[1])]
        else:
            cur = ROOT
    ans.append(-1 if cur == ROOT else cur.c)
print(*ans)

F - Hammer 2

最初、グラフを作ってクリティカルパスを調べて解けないか？と思って考えていましたが力尽きました。その方針で解けるのか？まだ気になりますが、ここでは解説の方法でやります。区間DPという新しいDPが出てきました。最近、過去にやったDPをまとめてふり返る機会を作り、これでちょっとDPに慣れたかなぁと思ったあとで、挿入DPが出てきて、さらにこの問題で区間DPが出てきました。まだあるんかい！と衝撃を受けています。到達した両端がLとRの状態でDPする、その情報を頼りにどうやって遷移していくのか？考えて、ようやくやり方がわかるまで苦労しました。Lにいる場合とRにいる場合も分け、L+1にLから行く場合とRから行く場合、R+1にLから行く場合とRから行く場合を計算していくんですね。見ての通りif分岐が多く、コードが長くなり苦労が見えます。ハンマーのインデックスを負数にすることで、壁と区別し、また、ゴールと原点のインデックスは0としました。このあたりの実装方針がこれで良かったのか？判断がむずかしいですが、ACにたどり着くことができました。入手済みハンマーを覚えておくところもややこしいですよね。 2023-01-03

N, X = map(int, input().split())
levents = [(0, 0)]
revents = [(0, 0)] # origin id 0 posi 0
if X > 0:
    revents.append((0, X)) # set goal id 0
else:
    levents.append((0, X))
# wall idx is +
for i, y in enumerate(map(int, input().split())):
    if y > 0:
        revents.append((i+1, y))
    else:
        levents.append((i+1, y))
# hammer idx is -
for i, z in enumerate(map(int, input().split())):
    if z > 0:
        revents.append((-i-1, z))
    else:
        levents.append((-i-1, z))
revents.sort(key=lambda x:x[1])
levents.sort(key=lambda x:-x[1])
rnum = len(revents)
lnum = len(levents)
rdp = [[-1]*rnum for _ in range(lnum)]
ldp = [[-1]*rnum for _ in range(lnum)]
rdp[0][0] = 0 # [l][r]
ldp[0][0] = 0
lhammers = set()
ans = -1
for i in range(lnum):
    ni = i + 1
    l  = levents[i]
    if l[1] == X:
        break # no need to move any more
    if l[0] < 0: # hammer
        lhammers.add(l[0])
    hammers = set(lhammers)
    for j in range(rnum):
        nj = j + 1
        r  = revents[j]
        if r[1] == X:
            break # no need to move any more
        if r[0] < 0:
            hammers.add(r[0])
        if ni < lnum: # update ldp next
            nl = levents[ni]
            if nl[0] <= 0 or nl[0] > 0 and -nl[0] in hammers:
                if rdp[i][j] != -1:
                    next = rdp[i][j] + r[1] - nl[1] # r->l
                    ldp[ni][j] = next if ldp[ni][j] == -1 else min(ldp[ni][j], next)
                if ldp[i][j] != -1:
                    next = ldp[i][j] + l[1] - nl[1] # l->l
                    ldp[ni][j] = next if ldp[ni][j] == -1 else min(ldp[ni][j], next)
                if nl[1] == X and ldp[ni][j] != -1:
                    if ans == -1:
                        ans = ldp[ni][j]
                    else:
                        ans = min(ans, ldp[ni][j])
        if nj < rnum: # update rdp next
            nr = revents[nj]
            if nr[0] <= 0 or nr[0] > 0 and -nr[0] in hammers: # can break r
                if rdp[i][j] != -1:
                    next = rdp[i][j] + nr[1] - r[1] # r->r
                    rdp[i][nj] = next if rdp[i][nj] == -1 else min(rdp[i][nj], next)
                if ldp[i][j] != -1:
                    next = ldp[i][j] + nr[1] - l[1] # l->r
                    rdp[i][nj] = next if rdp[i][nj] == -1 else min(rdp[i][nj], next)
                if nr[1] == X and rdp[i][nj] != -1:
                    if ans == -1:
                        ans = rdp[i][nj]
                    else:
                        ans = min(ans, rdp[i][nj])
print(ans)

G - Row Column Sums 2

最終的にDPの問題として解きましたが、自力ではできませんでした。DPをもっと解けるようになりたいですが、問題Gを自力で解いたのは過去1回しかないですし、まだまだ困難です。この問題はDPかなぁとも思ったのですが、最初別の方法で解けるのではないか？と思って試行錯誤していました。その時に少し考えを進めたあとで、RとCの1と2が同じ個数と勘違いしていて、心折れて解説を見ました。R方向に遷移していくDPで、残り2の列の個数をインデックスにすればよいとのこと。確かに、それまでに通った行を見れば、残った数字を計算でき、よって残り2の列の個数から残り1の列の個数も得ることができるので、これでいけます。こういったDPの式を、自力で思いつけるようになりたいものです！ところで、Python3でACしている30人ほどの中で、ぼくの処理速度が下から2番目の2408msだったのは少し気になります。この問題に関しては、配るDPより貰うDPの方が効率的で、処理速度が速くなりそうです。が、思考の流れが配るDPだったので配るDPで実装しました。書き換えるのは面倒です。貰うDPでやる強い意志を持って、その方針でささっと式を書くスキルは必要な場面が多そうですね。 2023-01-03

import sys
N = int(input())
mod = 998244353

# https://atcoder.jp/contests/abc273/submissions/37708024
# 階乗やchoose省略

R = list(map(int, input().split()))
sumR = sum(R)
sumC = 0
count2 = 0
for c in map(int, input().split()):
    sumC += c
    if c == 2:
        count2 += 1
if sumR != sumC:
    print(0)
    sys.exit()
dp = [0]*(N+1) # 2 left
dp[count2] = 1
sum_left = sumR
for i in range(N): # i->i+1
    if R[i] == 0: # do nothing
        continue
    dp_next = [0]*(N+1)
    for x in range(N+1):
        if dp[x] == 0:
            continue
        y = sum_left - 2*x
        if y < 0:
            break
        if R[i] == 1:
            if x > 0:
                dp_next[x-1] += dp[x] * x
                dp_next[x-1] %= mod
            dp_next[x] += dp[x] * y
            dp_next[x] %= mod
        elif R[i] == 2:
            if x > 1:
                dp_next[x-2] += dp[x] * choose(x, 2)
                dp_next[x-2] %= mod
            if x > 0:
                dp_next[x-1] += dp[x] * x
                dp_next[x-1] += dp[x] * x * y
                dp_next[x-1] %= mod
            if y > 1:
                dp_next[x] += dp[x] * choose(y, 2)
                dp_next[x] %= mod
    sum_left -= R[i]
    dp = dp_next
print(dp[0])

AtCoder Beginner Contest 274

ようやく初回以来の4問正解できました。これまで参加したABCの正解数は4,3,3,2,3,4です。初回にビギナーズラックなのか？4問正解でベストの成績を収め、その後低迷していたので、ようやく4問正解にたどり着けて嬉しいです。問題D - Robot Arms 2で、p2​=(A1​,0)というp2だけは+方向確定という条件を見逃していて、テストケース1つ不正解になる原因がわからず、残り30秒で気づいて正解するという奇跡を演じました。ミスったら不正解のまま終了という手に汗握る状況で正解できました。この罠にハマってなかったら問題Eを30分くらい考えられたのではないか？問題Eはたまに簡単なこともあるし解けたかもしれない。と悔しかったですが、問題Eはむずかしく、時間があってもどうせできませんでしたので、今回の4問正解は実力だなと納得しています。

E - Booster

わからなくて解説見ましたが、S\{i}というのは集合Sからiを除くという意味のようですね。これを知らなかったので、解説の理解にも手こずりました。いつも考え方を理解したあと、まずは自力で実装してみるのですが、bitDPのビットフラグの部分を、通過点のセットのタプルで表現し、dictを使ってやりましたところ、順当に時間制限にひっかかりました。で、解答例を見ました。なかなかエグいです。ビット演算を使いまくってるのはビット演算に慣れるのにいいですね。注意点として覚えたのは、&などのビット演算子の優先順位は+などの演算子より低いということ。なのでビット演算子を使う時()で囲っておいたほうが無難だなと思いました。知らない言葉も覚えました。popcountというのはビットが1の桁の数のようです。この問題ではboosterの回数を調べるのに5bitの整数のpopcountが必要なので、最初に計算してリストを作成していました。作り方もおもしろいです。ちなみに、Python3.10でint.bit_count()が追加されましたが、AtCoderでは使えませんね。hypotというのは2乗和の平方根らしいです。hypotenuse（ハイポテニュース）の略で、斜辺という意味です。平方根の計算をするときにmath.sqrtを使うのが当たり前と思っていましたが、**0.5と0.5乗する方法もあることも知りました。ぼくは距離は最初に全部計算して覚えておくように実装しました。この問題で最後に気になったのはdpのループの順序がこれで問題ないのか？ということです。通過した場所のリストをn+m桁のビットフラグで持っていて、for s in range(1, 1<<(n+m))のようにループさせてdpを更新しています。これでいいのか？ということです。考えてみると、これでいいということがわかりました。現在見ている[s]を更新できる条件は、sの部分集合の[sub_s]がすでに更新されていることですが、ビットフラグで考えるとsub_sのビットはsのビットの一部であることから、sub_s < sであることは明らかです。なのでこのループ処理において、[s]を更新する時点ですべての[sub_s]は更新されていることがわかります。なので、これで良いのです。最初に自力で実装したときは、popcountが小さい順じゃなければならないのではないかと思って、popcountをインクリメントしながらループして、combinationでsを作ってましたからね。そりゃあいろいろと重い。bitDP、クレイジーですね。 2022-10-23

popcount = [0]*32
for i in range(1, 32):
    popcount[i] = popcount[i>>1] + (i&1) # + > &
n, m = map(int, input().split())
nodes = [(0,0)]
for _ in range(n+m):
    nodes.append(tuple(map(int, input().split())))
dists = [[0.0]*(n+m+1) for _ in range(n+m+1)]
for i in range(n+m+1):
    for j in range(n+m+1):
        if j == i:
            continue
        if j < i:
            dists[i][j] = dists[j][i]
        dx = nodes[i][0] - nodes[j][0]
        dy = nodes[i][1] - nodes[j][1]
        dists[i][j] = (dx*dx + dy*dy)**0.5
# initialize
dp = [[1e12]*(1<<(n+m)) for _ in range(n+m)]
for i in range(n+m):
    dp[i][1<<i] = dists[0][i+1] #index+1 in dists
for s in range(1, 1<<(n+m)):
    boost_count = popcount[s>>n]
    for i in range(n+m):
        if not s & (1<<i):
            continue
        for j in range(n+m):
            if s & (1<<j):
                continue
            # i in s, j not in s
            new_time = dp[i][s] + dists[i+1][j+1]*0.5**boost_count
            if new_time < dp[j][s|(1<<j)]:
                dp[j][s|(1<<j)] = new_time
res = 1e12
for s in range((1<<n)-1, 1<<(n+m), 1<<n):
    boost_count = popcount[s>>n]
    for i in range(n+m):
        time = dp[i][s] + dists[i+1][0]*0.5**boost_count
        if time < res:
            res = time
print(res)

F - Fishing

わからなかったので解説の考え方を見ました。ある時刻において「左端に魚が必ずいる状態を調べれば良い」ということまでは自力でわかっていたのですが、その先の発想の転換ができませんでした。「時刻tではなくfish[i]に注目する」という視点の転換は、プログラミングにおいて、あるあるパターンだと思います。「左端に魚がいる状態を見ればいい」→「左端の魚を固定してみる」これが自然に思いつくようになりたいです。で、そこまでわかっても、Pythonで時間制限を突破するのはしんどかったです。最初heapqでイベントの発生順を管理しようとしましたが、全然間に合いませんでした。しかもPythonで間に合わせるユーザー解説に書いてあるように、ぼくもタプルをheapqにつっこんでました。無駄に第2要素の重さも見てしまってるようだし、いろいろ重い。時間のsetと、時間をキーとする重さの変化のdictを別々に管理してようやく間に合いました。Pythonで正解するにはノウハウがいろいろ必要ですね。いもす法なんですが、当たり前すぎていもす法とか言わないんでしょうか。笑。  2022-10-24

from collections import defaultdict
n, a = map(int, input().split())
fish = [tuple(map(int, input().split())) for _ in range(n)]
# w x v
res = 0
for i in range(n):
    # watch fish[i]
    imosuplus = defaultdict(int)
    imosuminus = defaultdict(int)
    times = set()
    for j in range(n):
        if i == j:
            continue
        v_rel = fish[j][2] - fish[i][2]
        if v_rel == 0:
            if fish[i][1] <= fish[j][1] <= fish[i][1]+a:
                times.add(0.0)
                imosuplus[0.0] += fish[j][0]
        elif v_rel > 0: # j is faster
            if fish[j][1] <= fish[i][1]+a:
                if fish[i][1] <= fish[j][1]:
                    times.add(0.0)
                    imosuplus[0.0] += fish[j][0]
                else:
                    time = (fish[i][1]-fish[j][1])/v_rel
                    times.add(time)
                    imosuplus[time] += fish[j][0]
                timeout = (fish[i][1]+a-fish[j][1])/v_rel
                times.add(timeout)
                imosuminus[timeout] -= fish[j][0]
        elif v_rel < 0: # i is faster
            if fish[i][1] <= fish[j][1]:
                if fish[j][1] <= fish[i][1]+a:
                    times.add(0.0)
                    imosuplus[0.0] += fish[j][0]
                else:
                    time = (fish[i][1]+a-fish[j][1])/v_rel
                    times.add(time)
                    imosuplus[time] += fish[j][0]
                timeout = (fish[i][1]-fish[j][1])/v_rel
                times.add(timeout)
                imosuminus[timeout] -= fish[j][0]
    weight = fish[i][0]
    if weight > res:
        res = weight
    for time in sorted(list(times)):
        weight += imosuplus[time]
        if weight > res:
            res = weight
        weight += imosuminus[time]
print(res)

G - Security Camera 3

問題の内容がシンプルでとっつきやすいので、自力で解けるんじゃないかと錯覚しましたが、いろいろな新しいことを勉強しなければ、ぼくには解けない問題でした。右方向と下方向のカメラだけ考えれば良くて、'.'が連続して並んでるところは1つのカメラで監視できます。すべての'.'をどちらかのカメラで監視するには最低いくつのカメラが必要か？というように、問題を読み替えられます。単純だし、全部右方向だけでもそこそこいい答えが得られそうじゃないですか。でも簡単ではありませんでした。この問題を通じて新しい言葉やアルゴリズムを覚えることとなりました。右方向のカメラのノードセット1、下方向のカメラのノードセット2を考え、それらの間をエッジ（'.'に相当）でつなぐグラフの問題となります。このような、ノードが2つのグループに分けられて、同じグループ内のノードは隣接していないようなグラフを「2部グラフ」と呼びます。最小数のノードを選択することですべてのエッジをカバーするにはどうすればよいか？という問題だということがわかりますが、それを「最小点カバー」「最小点被覆」と呼びます。さらに、2部グラフの「最小点カバー」は「最大マッチング」と一致するため、「最大マッチング」を解く問題に帰着します。（追記：マッチングの片方の点を選んでカバーできるということです。）なぜ「最小点カバー」と「最大マッチング」が一致するのかというと、グループ1のマッチしていない点Aの隣接点は必ずマッチしています。なぜなら隣接点もマッチしていないなら新しいマッチングが作れるので「最大マッチング」になってなかったことになりますから。グループ2のマッチしていない点Bについても同様です。では、Aの隣接点とBの隣接点同士がマッチしていることがあるかというと、それはありません。もしそうなっていると、Aと隣接点、Bと隣接点で2つマッチを作ったほうが良いことになり、この場合も「最大マッチング」になってなかったことになりますから。そのように考えを進めると、「最小点カバー」は「最大マッチング」と一致することがわかります。では「2部グラフ」の「最大マッチング」はどのように求めるのか？Source（s）ノードからグループ1のすべてのノードにつながっており、グループ2のすべてのノードがSink（t）につながっているようなグラフを考え、「最大流」を求めることで、「最大マッチング」を得ることができます。「最大流」を求めるにはFord-Fulkersonアルゴリズムを使います。sからtに流せるルートが無くなるまで、深さ優先探索をやり続けるという方法です。すでに流したエッジは、流量を減らすことで逆方向に流すことができると考えるのが味噌です。なぜ、Ford-Fulkersonで最大流量が求まるか？処理が終わるとtまで流せなくなったので、まだ流せる頂点の集まりSを考えます。これを残余グラフと呼びます。（Sから出ていく流量）-（Sに入ってくる流量）が現在求まっている総流量のはずです。ここで（Sから出ていく流量）は、キャパ限界で、（Sに入ってくる流量）は0となっているはずです。そうでないなら、流量を減らす余地があることになり、残余グラフSをもっと広げられることになるからです。よって、Sからこれ以上出ていくことができない状態になっていることがわかりますので、化かされたようなロジックですが、最大流量は確かに求まっていることがわかります。しかしFord-Fulkersonは効率的ではなく、最初このアルゴリズムを使ってやってみたらTLE（Time Limit Exceeded）でした。Dinic法という、より速い方法があります。Ford-Fulkersonは何も考えずにDFSを繰り返しますが、Dinic法では、BFSで各頂点へのSからの距離を計算し、一番短い経路から順にDFSします。これで速くなるというのがぼくにはあまり直感的ではありませんが、Ford-Fulkersonに比べて、処理がとても秩序だっていることはわかります。Dinic法を実装することで、ようやくACすることができました。この問題は、非常にシンプルで自力でいけそうでしたが、解くために新しい言葉を覚え、苦労してアルゴリズムを理解し、何ステップも経てのACで、勉強になりました。 2022-11-02

import sys
from collections import defaultdict
h, w = map(int, input().split())
s = []
cam_wdir = [[0]*w for _ in range(h)]
cam_cur = 0 # source
g = defaultdict(list)
for i in range(h):
    gap = True
    s_row = input()
    s.append(s_row)
    for j, c in enumerate(s_row):
        if c == '.':
            if gap == True:
                cam_cur += 1
                gap = False
                g[0].append([cam_cur, 1, len(g[cam_cur])])
                g[cam_cur].append([0, 0, len(g[0])-1])
            cam_wdir[i][j] = cam_cur
        if c == '#':
            gap = True
camlist_hdir = []
for j in range(w):
    gap = True
    for i in range(h):
        if s[i][j] == '.':
            if gap == True:
                cam_cur += 1
                gap = False
                camlist_hdir.append(cam_cur)
            g[cam_wdir[i][j]].append([cam_cur, 1, len(g[cam_cur])])
            g[cam_cur].append([cam_wdir[i][j], 0, len(g[cam_wdir[i][j]])-1])
        if s[i][j] == '#':
            gap = True
cam_cur += 1 # sink
if cam_cur == 1:
    print(0)
    sys.exit()
for i in camlist_hdir:
    g[i].append([cam_cur, 1, len(g[cam_cur])])
    g[cam_cur].append([i, 0, len(g[i])-1])
from collections import deque
level = []
def bfs(s):
    global g
    global level
    level = [-1]*len(g) # initialize level
    level[s] = 0
    q = deque([s])
    while q:
        v = q.popleft()
        for e in g[v]:
            if e[1] and level[e[0]] < 0:
                level[e[0]] = level[v] + 1
                q.append(e[0])
watch = [0]*len(g)
def dfs(v, t, f):
    global g
    global watch
    global level
    if v == t:
        return f
    for i in range(watch[v], len(g[v])):
        watch[v] = i
        e = g[v][i] # e = [to, capa, rev_id in g[to]]
        if e[1] and level[e[0]] > level[v]:
            d = dfs(e[0], t, min(f, e[1])) # f=e[1]=1 in this problem
            if d > 0: # d must be 1 in this problem
                e[1] -= d
                g[e[0]][e[2]][1] += d
                return d
    return 0
flow = 0
while True:
    bfs(0)
    if level[len(g)-1] < 0:
        break
    watch = [0]*len(g)
    while True:
        f = dfs(0, len(g)-1, 1)
        if f == 0:
            break
        flow += f
print(flow)

PyPyではなく、Pythonを使えば、NetworkXというライブラリを使うことができ、NetworkXには2部グラフの最大マッチングを求める関数も用意されているようです。それも試してみました。上のコードより少し処理時間が伸びましたが、ACできました。Hopcroft–Karpアルゴリズムを使っています。速そうですが、PyPy+自分で実装したDinicには勝てませんでした。NetworkXのhopcroft_karp_matchingを利用した2部グラフの最大マッチング計算は、以下のコードの最後の部分です。matchingのdictには逆方向のエッジも含まれるため、2で割る必要があります。 2022-11-02

import networkx as nx
h, w = map(int, input().split())
s = []
cam_wdir = [[0]*w for _ in range(h)]
cam_cur = 0
cams_wdir = []
for i in range(h):
    gap = True
    s_row = input()
    s.append(s_row)
    for j, c in enumerate(s_row):
        if c == '.':
            if gap == True:
                cam_cur += 1
                gap = False
                cams_wdir.append(cam_cur)
            cam_wdir[i][j] = cam_cur
        if c == '#':
            gap = True
es = []
cams_hdir = []
for j in range(w):
    gap = True
    for i in range(h):
        if s[i][j] == '.':
            if gap == True:
                cam_cur += 1
                gap = False
                cams_hdir.append(cam_cur)
            es.append((cam_wdir[i][j], cam_cur))
        if s[i][j] == '#':
            gap = True
B = nx.Graph()
B.add_nodes_from(cams_wdir, bipartite=0)
B.add_nodes_from(cams_hdir, bipartite=1)
B.add_edges_from(es)
matching = nx.bipartite.hopcroft_karp_matching(B, cams_wdir)
print(len(matching)//2)

AtCoder Beginner Contest 275

はじめて5問正解できました！前回まで4問を目指してがんばっていて、ようやく4問解けたところでしたが、その次の回で更新できるとは、ノッているようでうれしいです。問題Cは、頂点ペアを全探索し、それを1辺とする正方形があればカウントし、最後に4で割るという方法でやりましたが、処理時間は問題ありませんでした。問題Dは、最初f(10)くらいまで書き出してなにか規則がないかなどと考え始めましたが、f(n)を求めるのに、f(n/2)とかf(n/3)の値がわかればいいので結構計算が必要なところはスカスカであることに気づき、メモしながら再帰で解けました。問題Eは、逆元が必要な問題は過去に出会って計算方法を覚えていたので、そこでは悩みませんでした。確率の計算もこなれて、できたのかもしれません。Ratingが+169で665に伸びました。 2022-10-29

F - Erase Subarrays

DPだろうと思いながらも、どうすればいいかわからず、解説を読みました。確かに解説の通り、DPの式を作ることができます。これを自力で思いつけるようになるには、いろいろなパターンを解いていくしかないように思います。解説にdp[i][j][k]で、k=0のときaiを削除し、k=1のときaiを残すと書かれていますが、そのまま実装するとTLE（Time Limit Exceeded）となってしまいました。どうもPythonは、リストの数がパフォーマンスに大きく影響するようです。dp[i][j][k]だと、3次元目の要素数2のリストがN x M個作られることになります。これをdp[i][k][j]という順序にいれかえると、3次元目の要素数がMになり、リスト数はN x 2となり、この問題では1000分の1以下に削減できることになります。実際そのようにjとkを入れ替えるだけでACすることができました。制限時間2秒に引っかかっていたのに、431msで処理が終わりました。解説でdp[i][j][k]となっているのは理解しやすくて自然ですが、Pythonで解くには罠になっていました。高速に動作するためには、小さいリストをたくさん作るのを避け、大きなリストを少なく作るようにするべきです。メモ用の多次元リストは機械的に行列入れ替えられるはずなので、そのように実装すべきです。この問題から非常に重要な知見を得ることができました。 2022-10-30

n, m = map(int, input().split())
alist = list(map(int, input().split()))
dp = [[[3000]*(m+1) for _ in range(2)] for _ in range(n)]
dp[0][0][0] = 1
if alist[0] <= m:
    dp[0][1][alist[0]] = 0
for i in range(1, n):
    for j in range(0, m+1):
        dp[i][0][j] = min(dp[i-1][1][j]+1, dp[i-1][0][j])
        j_ = j - alist[i]
        if j_ >= 0:
            dp[i][1][j] = min(dp[i-1][1][j_], dp[i-1][0][j_])
for j in range(1, m+1):
    res = min(dp[n-1][0][j], dp[n-1][1][j])
    print(-1 if res >= 3000 else res)

G - Infinite Knapsack

今日は2022年12月1日。最近ABCの7問目である問題Gまでを、コンテスト終了後にACできるようになっています。ABC276、277、278、279は、やりました。昔はできてなかったのですが、力がついてきたのか、コンテスト終了後解説を見てACできているのです。非常に勉強になっているので、遡って問題Gまでを埋めていこうかなと思います。最初がこの問題で、最終的にはABCに参加し始めたところまで戻っていければと思います。この問題ですが、全部価値が1になるようにして解けば良く、Σxi = 1の条件で、max(Σai*xi, Σbi*xi)の最小値を求める問題であるというところまで、自力で問題を言い換えられていました。そこでなんとなく、力尽きたなぁと思って解説を見に行ったところ、凸包と書いてありました。自分で書いた式をよく見たらΣxi = 1で(Σai*xi, Σbi*xi)ってたしかに(ai, bi)の凸包ですね。冴えてたら気づけたと思うとちょっとくやしいです。で、凸包はこれを使えば良いと解説にありました。ロジックはわかりやすく、コピーして使います。この問題は、凸包の経験さえあればいけそうに感じました。問題Gの自力正解もちょっと近づいてきたような気がします。 2022-11-30

N = int(input())
points = []
for _ in range(N):
    a, b, c = map(int, input().split())
    points.append((a/c, b/c))
points.sort()
def cross(o, a, b):
    return (a[0]-o[0])*(b[1]-o[1]) - (a[1]-o[1])*(b[0]-o[0])
lower = []
for p in points:
    while len(lower) >= 2 and cross(lower[-2], lower[-1], p) <= 0:
        lower.pop()
    lower.append(p)
# upper = [] # upper[:-1]
# for p in reversed(points):
#     while len(upper) >= 2 and cross(upper[-2], upper[-1], p) <= 0:
#         upper.pop()
#     upper.append(p)
len_con = len(lower)
res = max(lower[0][0], lower[0][1])
if len_con > 1:
    for i in range(1, len(lower)):
        a, b = lower[i-1]
        c, d = lower[i]
        if d >= b:
            break
        res = min(res, max(c, d))
        t = (a-b)/(a+d-b-c)
        if 0.0 < t < 1.0:
            res = min(res, a+(c-a)*t)
print(1/res)

AtCoder Beginner Contest 276

家族で焼肉を食べに行ってたので、リアルタイム参加していません。翌日バーチャル参加し、問題A-Dの4完でした。4問解けたのは喜ばしいです。問題Cでなかなかバグを取れず45分くらいかかってしまいました。それでも問題Eに30分くらいかけられましたが、間に合いませんでした。ぼくの問題Eの方針は、壁伝いに進むというものだったのですが、うまく実装できず混乱に陥ってしまいました。笑。

焼肉

E - Round Trip

上記の通り、ハマってしまったため、解説を読みました。なるほど、シンプルですばらしいです。Sの上下左右の4点を始点として行ける限り行く。つながればOKということですね。自然に思いつきたいものです。ぼくが最初にやろうとしていた「壁伝いに行く」でも解けるのでしょうか？まあちゃんとやればいけるのでしょうけれども。 2022-11-06

import sys
from collections import deque
h, w = map(int, input().split())
cs = []
for i in range(h):
    cline = input()
    cs.append(list(cline))
    j = cline.find('S')
    if j >= 0:
        si = i
        sj = j
snexts = [(si+1,sj),(si-1,sj),(si,sj+1),(si,sj-1)]
for i, snext in enumerate(snexts):
    if 0 <= snext[0] < h and 0 <= snext[1] < w:
        if cs[snext[0]][snext[1]] == '.':
            q = deque([snext])
            while q:
                cur = q.pop()
                cs[cur[0]][cur[1]] = i
                if 0 <= cur[0]+1 < h:
                    if cs[cur[0]+1][cur[1]] == '.':
                        q.append((cur[0]+1,cur[1]))
                if 0 <= cur[0]-1 < h:
                    if cs[cur[0]-1][cur[1]] == '.':
                        q.append((cur[0]-1,cur[1]))
                if 0 <= cur[1]+1 < w:
                    if cs[cur[0]][cur[1]+1] == '.':
                        q.append((cur[0],cur[1]+1))
                if 0 <= cur[1]-1 < w:
                    if cs[cur[0]][cur[1]-1] == '.':
                        q.append((cur[0],cur[1]-1))
        elif isinstance(cs[snext[0]][snext[1]], int):
            print('Yes')
            sys.exit()
print('No')

F - Double Chance

k番目のカードを袋に追加したときに、期待値がどのように変化するのかまでたどりつき、フェニック木的なので高速に計算するんだろうなぁと思いながらそれ以上考えるエネルギーがなく、力尽きて解説を見ました。解説に、フェニック木を2つ作ると書いてあります。そこまでわかれば、あ～確かにいけそうだとなって実装し、ACできました。フェニック木といえば、初めて参加したABC266のEx - Snuke Panic (2D)で覚えた構造です。あの時は終わったあとの復習で、解説を見てExまでやらないといけないという強迫観念があり、むちゃくちゃつらい苦労をして1週間でACしたのでした。初めてでよくわかっていなかったからこそできたことでしたが、その後、初参加から3回目まではExをACするまでやりました。次ExをACするのはいつだろう？ABC266 Exで使ったのは2次元フェニック木でした。前回は最大値を求めるフェニック木でしたが、今回は合計ですね。2次元フェニック木だと空間計算量がでかくなりすぎることの回避策として、リストではなく辞書で実装します。今回は1次元ですが、最初は辞書のまま実装して提出しました。時間は1141msでした。 2022-11-07

m = 998244353
class BIT():
    global m
    def __init__(self, n):
        self.n = n
        self.sums = {}
    def add(self, i, input):
        while i <= self.n:
            if i in self.sums:
                self.sums[i] += input
            else:
                self.sums[i] = input
            self.sums[i] %= m
            i += i&-i
    def prod(self, i):
        res = 0
        while i > 0:
            res += self.sums.get(i, 0)
            i -= i&-i
        return res
n = int(input())
alist = [a for a in map(int, input().split())]
a_max = 2*10**5
fnum = BIT(a_max)
fsum = BIT(a_max)
top = 0
bottom = 1
for i, a in enumerate(alist):
    num_low = fnum.prod(a)
    sum_up = fsum.prod(a_max) - fsum.prod(a)
    top += (num_low*2 + 1) * a + sum_up*2
    top %= m
    inv_bottom = pow(bottom, m-2, m)
    print(top*inv_bottom % m)
    bottom += 2*(i+1) + 1
    bottom %= m
    fnum.add(a, 1)
    fsum.add(a, a)

なんか遅いなと思い、リストで作り直したところ、459msと、かなり速くなりました。 2022-11-07

class BIT():
    global m
    def __init__(self, n):
        self.n = n
        self.sums = [0]*(n+1)
    def add(self, i, input):
        while i <= self.n:
            self.sums[i] += input
            self.sums[i] %= m
            i += i&-i
    def prod(self, i):
        res = 0
        while i > 0:
            res += self.sums[i]
            i -= i&-i
        return res

G - Count Sequences

しばらく考えた後、あきらめて解説を見ました。解説を理解するのも苦労しました。解説者と自分の思考が同調しないというかなんというか、読めばすんなり入ってくるのではなくて、自分なりに再構築してようやくわかるので、解説を読むって大変ですね。ai+1とaiの差をbiとおく時点でやられたと思いました。でも問題の条件から、差を3で割った余りが1か2になることがわかるわけですから、自然といえば自然で、慣れてくるとこのような変形はできるようになるのかもしれません。ヒントは問題の中に隠されており、素直に考えれば思いつくのではないでしょうか？a1をp、M-aNをq、bi=3*yi+1+xiとおくと、条件は、M-n+1=p+q+3*Σyi+Σxiと変形できて見通しがよくなります。p、q、yiは非負整数、xiは0か1です。これでできる！と思ったのですが、まだまだダメでした。Σyiの取りうる値でループし、残りをp+q+Σxiに振り分けます。このとき、xiのうちいくつ1があるかでループすると、2重ループになり、計算量がO(MN)とかになってしまうのです。なんとかして2重ループを避けなければなりません。でも自力で考えてもどうにもわからん。この問題に関しては、「累積和」というテクニックを使って2重ループを回避できるようです。このように考えます。xiのみで合計sとなる組み合わせ数をf(s)とするとf(s)=choose(n-1,s)です。pとxiのみで合計sとなる組み合わせ数をg(s)とすると、g(s)=Σp(0→s)f(s-p)なので、g(s)=Σp(0→s)f(p)となります。pとqとxiで合計sとなる組み合わせ数をh(s)とすると、同様にh(s)=Σq(0→s)g(q)となることがわかり、h(s)はg(s)の累積和を2回計算すると求められることがわかります。h(s)を事前にO(N)で計算しておき、参照することで内側のループは不要になります。トリッキーで化かされたような気分です。pとqとxiで合計sにするとき、ループを回して足し算してしまうよなぁと思うんですよね。1度経験したことで、これは累積和かな？って今後思うのでしょうか？ 2022-11-09

import sys
mod = 998244353
n, m = map(int, input().split())
sum = m - n + 1
if sum < 0:
    print(0)
    sys.exit()

count_max = max(n - 1, sum//3 + n -2)
fact = [0]*(count_max+1)
invfact = [0]*(count_max+1)
fact[0] = 1
for i in range(1, count_max+1):
    fact[i] = fact[i-1] * i % mod
invfact[count_max] = pow(fact[count_max], mod-2, mod)
for i in range(count_max-1, 0, -1):
    invfact[i] = invfact[i+1] * (i+1) % mod
invfact[0] = 1
def choose(a, r):
    return fact[a] * invfact[r] * invfact[a-r] % mod

two_max = min(sum, n-1)
g = [0]*(two_max+1)
for i in range(two_max+1):
    g[i] = choose(n-1, i)
for i in range(1, two_max+1):
    g[i] = (g[i] + g[i-1]) % mod
if sum > n-1:
    keep = g[n-1]
for i in range(1, two_max+1):
    g[i] = (g[i] + g[i-1]) % mod

ans = 0
for threes in range(sum//3 + 1):
    case_y = choose(threes+n-2, threes)
    left = sum - threes * 3
    ans += case_y * (g[left] if left < n else g[n-1] + keep*(left-n+1))
    ans %= mod
print(ans)

Ex - Construct a Matrix

今ならmod2の連立一次方程式であることは、2が奇数個含まれているときだけ、余り2になることからわかるので、今なら解けるかも、と、ふとこの問題を思い出してやってみたら、簡単ではありませんでした。Q=N=2000で、全頂点を変数にすると、条件だけでQN^2です。無理。XORの2次元累積和を取ることで、4隅のXOR累積和だけを変数として連立方程式を作れるとのことです。4Q^2に減ります。これは気づけない。0は、1つ含まれていれば0になってしまうから、1か2の領域と被ってないことをチェックするだけでしょ。と思ったらこれも結構大変で、2次元いもすからの2次元累積和で処理しました。その後もとにかくバグ取りが大変で、解いた連立方程式の解に自由度があると思うのですが、それによって03_smallzero_01-04あたりのテストケースはダメパターンに陥りました。0でなければならないところを、2にしてしまう解があるということです。どうやって回避すればいいのかわからないのですが、結局0でなければならないところは、無理やり0にするという処理を入れたらなぜかACできました。なぜこれでいいのかわかってないので、もしかしたらバグっているかもしれません。まあ、可能な解でループする処理を入れて、0を2にしてしまったら次の解でやってみるというのが自然な回避方法でしょうね。その処理を書いたことがないし、やったほうがいいですが、もう余力がないです。久しぶりのEx ACで勉強になるところは多かったです。 2023-03-11

Submission #39594348 - AtCoder Beginner Contest 276

AtCoder Beginner Contest 277

4完でした。問題Eに40分残っていました。問題Eは、難しいなと思いましたが、スイッチをコスト0の辺とみなすことに時間内にひらめき、なんとか解こうとがんばりましたが間に合いませんでした。始めた当初なら、これに気づけることなどありえなかったことなので、自分にとってうれしいことですが、解けてる人多すぎです。こんなトリッキーでも、ありがちなパターンなんだろうなぁと思いました。入緑を目指していましたがならず。終わったあと提出したら、なぜか実行時エラー発生。翌朝再チャレンジでACできましたが、その過程でダイクストラ法のロジックにミスっている箇所を発見し、勉強になりました。 2022-11-12

E - Crystal Switches

a=1の辺に対応する頂点を1からN、a=0の辺に対応する頂点をN+1から2*Nとなるように分離してグラフを作ります。スイッチはsとs+Nをつなぐコスト0の辺とみなします。そこからダイクストラ法を使って解きました。heapqにタプルを入れることに抵抗がありますが、そのように実装しました。最初、テストケース001.txtと003.txtがRE（実行時エラー）となって原因不明でした。翌朝やり直したときにダイクストラ法の実装に不備があることに気づきました。# needless cost maybe registered in pqとコメントを書いた箇所です。危ないです。勉強になりました。 2022-11-13

from collections import defaultdict
n, m, k = map(int, input().split())
edges = defaultdict(set)
switches = {}
for _ in range(m):
    u, v, a = map(int, input().split())
    if a == 0:
        u += n
        v += n
    edges[u].add(v)
    edges[v].add(u)
if k != 0:
    for s in map(int, input().split()):
        switches[s] = s+n
        switches[s+n] = s
costs = [-1]*(2*n + 1)
costs[1] = 0
import heapq
pq = [(0, 1)]
while pq:
    cur = heapq.heappop(pq)
    cost = cur[0]
    v = cur[1]
    if cost > costs[v]:
        # needless cost maybe registered in pq
        continue
    for next in edges[v]:
        if costs[next] == -1 or cost+1 < costs[next]:
            costs[next] = cost+1
            heapq.heappush(pq, (cost+1, next))
    if v in switches:
        next = switches[v]
        if costs[next] == -1 or cost < costs[next]:
            costs[next] = cost
            heapq.heappush(pq, (cost, next))
if costs[n] == -1:
    print(costs[2*n])
elif costs[2*n] == -1:
    print(costs[n])
else:
    print(min(costs[n], costs[2*n]))

F - Sorting a Matrix

あわよくば、自力で解けるのではないか？そんな淡い期待を胸に、次の問題、次の問題と進んでいってしまいます。そして問題は解けず、時間が溶けていきます。でも時間が溶けることはネガティブなことではありません。その時間、確実に学んでいるわけですから。この問題Fを自力で解くことはできませんでした。知らない概念が必要な問題で、とても勉強になりました。新しい問題に挑戦するたびに、知らないことがどんどん出てくるからやめられません。解けなかった問題が解けた時、確実に1歩前進しているわけですから。0は無視でいいな。H方向はなんとかなるな。W方向は置換？うーんわからん。ということで解説を読みます。グラフの問題だったんですね。驚きます。新たに学んだ言葉は、「トポロジカルソート」「DAG（Directed Acyclic Graph）（有向非巡回グラフ）」です。W方向は、列を1つの頂点と考え、小さい数字から大きい数字に有向辺を張ります。そうしてできたグラフを「トポロジカルソート」できるならば、条件を満たす置換ができます。しかしそのまま実装するとH x choose(W,2)=O(HW^2)本も辺を作ることになってしまいます。これをO(HW)にする方法が書かれていますが、エグいですね。一般的なやり方なんでしょうか？さて、「トポロジカルソート」できる条件が「DAG」である（巡回路がない）ことです。では「DAG」であることをどのように判定するのでしょうか？Kahnの方法（1962）を使います。入力がない頂点のセットSを作ります。そこから辺をたどっていき、たどった辺を消していきます。辺を消したことで入力がなくなった頂点も頂点セットSに追加し、さらにたどっていきます。頂点セットSが空になった時、まだ入力辺が残っている頂点があれば、このグラフには巡回路があり、「DAG」ではないことがわかります。逆にすべての頂点の入力辺が消えていたら「DAG」です。たしかに巡回路があると、その巡回路に含まれる頂点は、この処理が完了しても、入力辺が0になることがありません。なぜならその頂点の入力辺が0になるためには、巡回路の中の1つ前の頂点からの入力が消えなければならず、つまりその頂点がSに追加されなければなりません。そのためには巡回路の中の1つ前の頂点が…。とぐるぐる回ってしまうからです。これで「DAG」判定ができるようになりました。さて、実装したのですが、TLEが4つ出てしまいました。テストケースの002、005、006、007です。最初に、グラフなどの構造をdict（実際にはdefaultdict）を使って表現していましたが、これを全部リストにしました。これでテストケース002をACできました。IDがスカスカであれば、dictを使ってメモリ使用量を抑える効果がありますが、隙間なく頂点のIDを使うのであれば、listを使うべきですね。2次元フェニック木とかで空間計算量を抑えるためにdictを使うというようなことを覚えたせいで、なんかdictを使ってしまいがちです。無駄にdictを使わないというのは大事なことだと思います。次にinputを高速化しました。以下のように追記します。これ、本当に効くので、今後は入れたほうが良いと知りました。

import sys
input = sys.stdin.readline

それでもテストケース005、006、007がTLEのままでした。H方向のmin-max区間が被っていないことのチェックをいもす法みたいな処理でやっていたのですが、これが該当テストケースにおいて、むちゃくちゃ遅かったようです。シンプルに(min, max)のリストを作ってソートしてからループを回し、prev_max<=cur_minをチェックすればよかったのです。これで遅かった3つのテストケースが一気に短時間で処理できるようになり、結果的に現時点でPython3のACの中で、2番目の速度を出すことができました。TLEから2位へ。ちょっとした修正でこんなに速くなるとは、わけがわかりませんね。いもす法バージョンは、dictに{min:+1, max:-1}のような合計を計算しておいて、ソートして小さい順に計算し、合計が2以上になったら被っていると判定していました。dictを使っていること、それをソートするときにlistに変換されることなどオーバーヘッドは確かにありますが、こんなに効くとは。結局、最終的なコードではdictを全く使っていません。dictとlistの使い分けは、速度の観点で要注意であると、強く思いました。dictよりlistを使え。というわけで、ヨシっ！やっとACできた。この問題の解き方の、頂点を追加してグラフを作るところ、美しいし、頭の中でイメージするだけで楽しくなってしまうような解き方だなぁと感じています。 2022-11-14

import sys
input = sys.stdin.readline
h, w = map(int, input().split())
vnext = w
minmax_list = []
graph_updated = False
graph = [[] for _ in range(w)]
from_count = [0]*w
for _ in range(h):
    alist = list(map(int, input().split()))
    aset = set(alist)
    aset.discard(0)
    a_unique_num = len(aset)
    if a_unique_num > 1:
        graph_updated = True
        a_unique_sorted = sorted(aset)
        amin = a_unique_sorted[0]
        amax = a_unique_sorted[-1]
        minmax_list.append((amin,amax))
        a2v = {a : vnext+i for i, a in enumerate(a_unique_sorted)}
        graph.extend([[] for _ in range(a_unique_num-1)])
        from_count.extend([0]*(a_unique_num-1))
        for i in range(w):
            a = alist[i]
            if a == 0:
                continue
            interv = a2v[a]
            if a != amin:
                graph[interv-1].append(i)
                from_count[i] += 1
            if a != amax:
                graph[i].append(interv)
                from_count[interv] += 1
        vnext = a2v[amax]
# check h dir
minmax_list.sort()
prevmax = 0
for x in minmax_list:
    if x[0] < prevmax:
        print('No')
        sys.exit()
    prevmax = x[1]
# h dir ok, then check w dir
if not graph_updated:
    print('Yes')
    sys.exit()
starters = [v for v in range(len(from_count)) if from_count[v] == 0]
if not starters:
    print('No')
    sys.exit()
# check DAG
while starters:
    v = starters.pop()
    for next in graph[v]:
        from_count[next] -= 1
        if from_count[next] == 0:
            starters.append(next)
for count in from_count:
    if count:
        print('No')
        sys.exit()
print('Yes')

G - Random Walk to Millionaire

解説を見るしかないわけですが、またクレイジーですね。解説を理解できるまでに何ステップも「あ、そういうことか！」が必要で大変です。そして理解が進むほど「狂ってる！」と感動します。何も工夫せずにやろうとすると、レベルの状態が多すぎて、1つの行動だけでNK=9000000も状態が必要になってしまいます。通り道のCv=0の個数がX個のときレベルXとなり、Cv=1での獲得金額はX^2となります。これをX^2=choose(X,2)*2+Xと変形すると、通り道のCv=0から2つ選ぶ場合の数と、通り道のCv=0から1つ選ぶ場合の数を計算すれば、獲得金額を計算できることがわかり、各頂点に3つの状態のみ必要なDPに帰着できます。驚くべき問題の読み替えで、狐につままれたような気分です。なんでこんなことになるのでしょうか？途中で獲得するお金は、Cv=1に着くたびに確率をかけて累積していけばよいです。期待値を計算するときのこの感覚を自然だと思えるよう、身につけておきたいところです。さて、いつものようにTLEとなり、速度改善をがんばってACできました。3つの状態のリストはつなげて3*nのサイズの1つのリストにしました。dpのリストをK回の行動分一気に作らず、前回と今回のみ作ってループしました。Fromでループすると全部終わってからもう一度ループを回してansを更新する必要があるので、Toでループし、その場でansを更新できるようにしました。同じ計算を2回しないようにしました。どれが効いたのかはわかりませんが、現在Python3での提出者中、3位の速度でACできました。素直にわかりやすくコードを書くとTLEになりがちなのはPythonのつらいところです。もちろん楽しんでますが、競技プログラミングで使用するならC++も検討すべきと感じていて、今後はちょっとずつC++でも解こうと思っています。問題Fに続き、信じられないような解法で感動したし、楽しかったです。 2022-11-15

mod = 998244353
n, m, k = map(int, input().split())
nexts = [[] for _ in range(n)]
for _ in range(m):
    u, v = map(int, input().split())
    u -= 1
    v -= 1
    nexts[u].append(v)
    nexts[v].append(u)
clist = list(map(int, input().split()))
rates = [0]*n
for v in range(n):
    rates[v] = pow(len(nexts[v]), mod-2, mod)
dp = [0]*(n*3)
dp[0] = 1
ans = 0
nx2 = n*2
for _ in range(k):
    dp_next = [0]*(n*3)
    for v in range(n): # to v
        for next in nexts[v]:
            in0 = dp[next] * rates[next]
            in1 = dp[next+n] * rates[next]
            dp_next[v] += in0
            dp_next[v+n] += in1
            dp_next[v+nx2] += dp[next+nx2] * rates[next]
            if clist[v] == 0:
                dp_next[v+n] += in0
                dp_next[v+nx2] += in1
            dp_next[v] %= mod
            dp_next[v+n] %= mod
            dp_next[v+nx2] %= mod
        if clist[v] == 1: # get money
            ans += dp_next[v+nx2] * 2 + dp_next[v+n]
            ans %= mod
    dp = dp_next
print(ans)

Ex - Constrained Sums

強連結成分分解、トポロジカルソート、2-SAT、そしてこの問題自体の言い換え、と、何日かかけてがんばっていろいろ理解し、久しぶりにExをACしたいと試みましたが、サンプルケースもACできませんでした。ていうか提出したらほとんどのテストケースで、グラフを作るところだけでTLEになってました。くやしいですが一旦あきらめます。よく見たらPythonでACしてる人が2人しかいません。それだけむずかしいのでしょうか？素人のぼくがPythonで3人目のACだとすごいですが、難しいですよねぇ。消耗しました。次のABC278 Exは1人しか解けなかったりと、問題Exは、素人が手を出したらエネルギーがなくなってひどいことになりそうです。もう少し力がつくまで距離を置こうと思います。ABCに参加し始めて最初の3回はExを無理やりACしたのですが、あれは始めたばかりでまだエネルギーがあったということでしょうか？笑。いや、あの時もFFTを理解するのに1ヶ月かかったり大変だったなぁ。勉強したことは身になったはずと前向きに捉えながら。 2022-11-20

「あきらめる」とか言いつつ、考え続けてしまうのはなんなんですかね。「考える」ってコントロールできないような気がします。一度やりはじめたら、やめようと思っても「考えちゃう」んですよね。ACできました！現時点で、PythonでACしてるのが3人しかいないし、提出者も6人しかいないです。なんか少ないな。どういうことでしょうか？競プロ素人のぼくが3人しかいないPythonでのACの中に入ってるなんて、なんか自信に繋がります！ExをACしたのは、ABC268以来で久しぶりです。実は参加開始して最初の3回はExを全部がんばって解いたんですよね。でも、これやり続けたら体が持たないと思って遠ざかっていたのです。今回もやはりきつかった。この問題について書きたいことは、この問題を通じて学んだことが多いので、多いです。しかし強連結成分分解の正当性とか、絵も描かないと説明できないかもなぁと思っていますし、2-SATに関しては、完全に解明できてない部分もあるような気がしていますが、反省会ということで書いていきます。最後の最後でTLEを解決したのは、強連結成分分解のDFSを再帰関数から、スタックを使う方法に変更したところです。ていうかsys.setrecursionlimit(10**6)としたら、自動的にPyPyじゃなくてPythonになってしまうんですね。スタックを使ってPyPyを使ったほうが速いというのは重要な知見です。この問題を解くのに使用している2-SATというのは、「充足可能性問題（satisfiability problem, SAT）」のうち、(A∨B)∧(C∨D)∧…という形式で、「または」の部分の論理式が2つ以下の問題のことです。2-SATに言い換えて解いているわけですが、これが気づける気がしない言い換えになっています。L<=A+B ⇔ ¬((A<0∧B<L+1)∨(A<1∧B<L)∨(A<2∧B<L-1)∨…∨(A<L+1∧B<0)) ⇔ (A>=0∨B>=L+1)∧(A>=1∨B>=L)∧…∧(A>=L+1∨B>=0)というように2-SATに言い換えています。同様に、A+B<=R ⇔ ¬((A>=0∧B>=R+1)∨…∨(A>=R+1∧B>=0)) ⇔ (A<0∨B<R+1)∧…∧(A<R+1∨B<0)と2-SATに言い換えています。条件はL<=A+B<=Rと、LもRも「<=」を使って表現されていますが、言い換えのときに、Lの方の論理式は「>=」で表現され、Rの方の論理式は「<」で表現することによって、Xと¬Xの関係に結びつけているのです。これを狙ってやっているのが、トリッキーで驚きました。信じられません。2-SATを表現するグラフに対して、強連結成分分解を行いXと¬Xが同じ強連結成分に入っていると、解が得られないことがわかります。強連結成分の中ではすべてTrueか、すべてFalseでなければならないからです。強連結成分分解後、トポロジカルソートを行い、Xと¬Xのうち、後ろにある方をTrueにすることで、解を得ることができます。といいつつこれって自明なんですかね？自明ではないと思うので説明が必要です。すべてのXと¬Xのペアが同じ強連結成分に入っていないことがわかり、TrueとFalseを割り当てたとき、同じ強連結成分内でTrueとFalseは全部一致しているのですか？全然自明ではありません。不整合が起きるというのは、Xと¬XのペアにTrue/Falseを割り当てたあと、A→Bというエッジが存在するにも関わらず、AがTrueでBがFalseとなっているということです。A→Bというエッジが存在し、AがTrue、BがFalseであれば、トポロジカルソートの結果は¬A、A、B、¬Bの順に並んでいるはずです。しかし、2-SATのグラフ生成方法から¬B→¬Aというエッジが存在するはずです。これは先程のトポロジカルソートの順序と矛盾するのです。なので、Xと¬Xが同じ強連結成分に含まれていなければ、True、Falseを割り当てたときに、不整合は起きないことがわかります。Aが必ずTrueであるという条件は¬A→Aで表すということで、いけそうです。この議論から、2-SATのグラフはきれいな形をしていそうだな、と思います。変なエッジを適当に加えるといろいろな条件が壊れてしまうのではないでしょうか？A→Bを加えるなら、必ず¬B→¬Aも追加する必要がありそうです。（ですよね。）この問題においては、L、Rの条件以外にX>=0は常にTrue、X<M+1は常にTrueという条件もグラフに追加しています。またX>=tであれば、X>=t-1である、という条件も追加しています。これらのエッジはグラフをきれいなまま維持します。これらのエッジは必要なのでしょうか？結論としては、追加するべきなのだろうと考えています。2-SATの問題は、条件が足りないと、トポロジカルソートの結果が十分定まらず、どちらがTrueでも良いという結果になりえます。なので、人間の頭で把握している条件（1より2が大きいとか）も追加しておくべきだと考えます。（あいまいな言い方しかできませんが。）また、全ノードにエッジがつながってわかりやすくて良いとも感じました。X>=aのときにX<aがFalseとなり、よってX<a-tもFalseということが満たされるので、X>=a∧X<a-tというような、不正な状態が起きないことを保証できるのも良いです。強連結成分分解のアルゴリズムの正当性も時間を使って考えました。最初のDFSでツリーがいくつかできますよね。2回目のエッジを逆向きに進むDFSでは、1本でもエッジがつながったらそりゃぁ確かに強連結成分です。最初のDFSで作った子孫からエッジが伸びてるということですから、すぐさま巡回路の完成です。2回目のDFSで、最初のDFSで作ったツリーの外には出れません。もし出れたら最初のDFSで、その外にあるツリーに含まれてたはずですよね。だから出れません。2回目のDFSのときに、最初のDFSで作ったツリーの中の部分木がいくつか残ったとします。2回目のDFSで別の部分木につながってしまうと、強連結成分じゃなくなってしまいそうです。しかし、2回目のDFSで、部分木の外には出れません。なぜなら最初のDFSで帰りがけ順に番号を振ったからです。2回目のDFSで別の部分木に移動できてしまうと、そっちの部分木の方が帰りがけ順であとになっていたはずなので、ありえないのです。最初のDFSで帰りがけ順に番号を振るのも、帰りがけ順であとになっていた方から2回目のDFSをやるのも、意味があるのです！このように、強連結成分分解、トポロジカルソートに2-SATと、この問題でもいろいろ考えて新しいことを学びました。大変でしたが、久しぶりにExをACできてうれしい！ 2022-11-21

import sys
input = sys.stdin.readline
# sys.setrecursionlimit(10**6)
N, M, Q = map(int, input().split())
M2 = M+2
HALF = N*M2
LENALL = 2*HALF
G = [[] for _ in range(LENALL)]
for i in range(N):
    i0 = M2*i
    G[i0+HALF].append(i0) # x>=0 is always True
    G[i0+M+1].append(i0+M+1+HALF)
    for j in range(M+1):
        ij = i0+j
        G[ij+1].append(ij) # x>=j+1 -> x>=j
        G[ij+HALF].append(ij+HALF+1)
for _ in range(Q):
    a, b, l, r = map(int, input().split())
    a -= 1
    b -= 1
    for j in range(M2): # a
        jj = l + 1 - j # b
        if 0 <= jj < M2:
            aj = M2*a+j
            bjj = M2*b+jj
            G[aj+HALF].append(bjj)
            G[bjj+HALF].append(aj)
        jj = r + 1 -j
        if 0 <= jj < M2:
            aj = M2*a+j
            bjj = M2*b+jj
            G[aj].append(bjj+HALF)
            G[bjj].append(aj+HALF)

# 省略 https://atcoder.jp/contests/abc277/submissions/36706989

ans = []
for i in range(N):
    base = i*M2
    min_ = 0
    for j in range(1, M+1): # check 1-M
        v = base + j
        if t_order[v] == t_order[v+HALF]:
            # need to check all
            print(-1)
            sys.exit()
        elif t_order[v] > t_order[v+HALF]:
            min_ = j
    ans.append(min_)
print(*ans)

AtCoder Beginner Contest 278

前回に続き、4完でした。問題Dで、ペナルティ3回食らってしまい順位を落としました。最初、クエリ1のときに毎回リストを0でリセットしてしまい、TLEでした。あ～確かに、と思い直してリセットフラグみたいなのを各要素に持たせましたが1発で処理の流れを整理しきれなかった感じです。立て直しを迅速にやる力は大事ですね。その後、問題Eに35分くらい残っていて、各数字のミニマックスボックスを作るところまでは思いついたのですが、プラスαで、なんかいもす法的なのを使わないと間に合わないと思いこんでしまい、解けませんでした。終了後にミニマックスボックスだけでやったらふつうにACできました。もったいないです。今回入緑できればと思っていましたが、残念ながらダメでした。問題Eが普通に解けていたらと思い、くやしいです。でもまあ、いつの間にか続けて4問以上解けるようになっているので、成長はしているのかな…。そういえば、今週はABC277 Exを解こうと思ってがんばっており、頭を酷使しすぎて本当にしんどいです。久しぶりにExをACするぞーと、つい始めてしまいました。まだできておらず、疲れ切って消耗しているので、数日でも競プロから距離を置いた方がいいかもしれないです。切実に。 2022-11-19

E - Grid Filling

終了後に、普通に全範囲をループして比較するだけでACできました。くやしいなぁ。ところで、この問題でdefaultdictの初期化時にlambda関数を引数で渡すというのを初めてやりました。今までdefaultdict(int)とかdefaultdict(list)とかしか作ったことなかったんですよね。指定した値で初期化されたリストを返す関数を渡すということをしました。いろいろ勉強していると、いつの間にか新しいことができるようになってますね。 2022-11-19

from collections import defaultdict
H, W, N, h, w = map(int, input().split())
grid = []
for _ in range(H):
    grid.append(list(map(int, input().split())))
# imin, imax, jmin, jmax
default_minmax = lambda : [H, -1, W, -1]
minmax = defaultdict(default_minmax)
for i in range(H):
    for j in range(W):
        a = grid[i][j]
        minmax[a][0] = min(minmax[a][0], i)
        minmax[a][1] = max(minmax[a][1], i)
        minmax[a][2] = min(minmax[a][2], j)
        minmax[a][3] = max(minmax[a][3], j)
num = len(minmax)
res = []
for i in range(H+1-h):
    imax = i + h - 1
    res_w = []
    for j in range(W+1-w):
        jmax = j + w - 1
        count = 0
        for v in minmax.values():
            if i <= v[0] and v[1] <= imax and j <= v[2] and v[3] <= jmax:
                count += 1
        res_w.append(num-count)
    res.append(res_w)
for res_w in res:
    print(*res_w)

F - Shiritori

bitDPでしょ、と思いながら自力ではできず、解説見ました。今週はABC277 Exなどチャレンジして砕け散り、エネルギーが消耗していてつらいです。ABCが毎週あると、素人にとっては毎回新しいことが出てくるので、休む暇がなくてつらいです。この問題、解説見るまでにいろいろ頭の中で考えました。しりとりって次の単語に接続していくので、グラフですよね。そして、出力がない単語を選んだら勝ちです。つまり、すべての単語に出力があるケースを考えたらいいわけですね。最近覚えたばかりの強連結成分分解か？とか、文字を頂点、単語をエッジとするグラフを考えるのか？などと、いろいろ考えておもしろかったですが、行き詰まりましたw。解説はbitDPでしたが、Pythonで提出していてやたら速い人達がたくさんいたので、中身をみると、しりとりのグラフを作ってDFSで解いていました。しかし1度使った単語を再度使わないことで1回のDFSをO(N)にしていたのですが、その正当性が理解できず、自分の中では納得できていません。でもDFSで解く方法も正しいのだと思います。これはいずれ理解しないといけないな、と思っています。以下のコードは解説の通りbitDPで実装したものです。bitDPもすでに2回目なので、すんなり実装できました。ただ、DPテーブルを次文字cから始める場合に勝てるかどうか？と決めることは、まだ容易ではありません。単語を選んだときに、後手はその単語の末尾の文字から始める必要があります。それで勝てない状態が1つでもあれば、先手は勝てることがわかり、DPテーブルを更新することができます。 2022-11-21

import sys
n = int(input())
d = {}
idx = 1
cset = set()
for _ in range(n):
    s = input()
    cset.add(s[0])
    cset.add(s[-1])
    d[idx] = [s[0], s[-1]]
    idx <<= 1
clist = list(cset)
dp = {c:[0]*(1<<n) for c in clist}
# dp[c][bit]
for s in range(1, 1<<n):
    if s in d: # 1bit
        dp[d[s][0]][s] = 1
    else:
        for c in clist:
            # update [c][s]
            scopy = s
            while scopy:
                idx = scopy&-scopy
                if d[idx][0] == c and dp[d[idx][1]][s-idx] == 0:
                    dp[c][s] = 1
                    break
                scopy -= idx
for c in clist:
    if dp[c][s] == 1:
        print('First')
        sys.exit()
print('Second')

やっぱりわからない…。これでACしてしまうけど、どう考えても、コメントアウトしたused[v] = Falseが必要。当初、他の方の回答を見て、なんでこれでACなんだろう？って思ったのが最初なんですよね。自分なりに再現させたのがこのコードです。 2023-01-10

N = int(input())
slist = []
for _ in range(N):
    slist.append(input())
g = [[] for _ in range(N)]
for i, s in enumerate(slist):
    for j, s in enumerate(slist):
        if i != j and slist[i][-1] == slist[j][0]:
            g[i].append(j)
used = [False]*(N)
def win(v):
    res = True
    used[v] = True
    for next in g[v]:
        if used[next]:
            continue
        else:
            if win(next):
                res = False
                break
    # used[v] = False # どう考えてもこれいるでしょ
    return res
for v in range(N):
    used = [False]*(N)
    if win(v):
        print('First')
        break
else:
    print('Second')

上のコードを、WA（不正解）にできるテストケースを作ることができました。こちらです。

4
ab
bc
cc
ca

何か得体の知れない数学の定理によって、このコードは正しいのか？と悩んでいたので、間違っていることは、テストケースを追加して証明するしかないですね。上のコードのコメントアウトによって1回のDFSが必ず頂点数、つまりこの問題では16回で終わり、処理がすぐ終わりますが、誤ったコードです。しかし、コメントアウトしたused[v] = Falseの部分を有効にすると、このままでは処理時間が膨大になってしまうケースがあります。たとえば16個の文字列がすべてaで始まってaで終わる場合、もっともエッジ数が多くなり、DFSの計算量は16!=2x10^13程度になってしまいます。エッジ数を減らすには、先頭の文字と終わりの文字の組み合わせが同じものをまとめることで、エッジ数を減らせば良いのではないでしょうか？そしてその個数を覚えておき、DFSの最中に通ったら1減らし、再帰関数を抜けるときには1増やして元に戻します。この場合、文字ペアがすべて異なるようにしつつエッジ数が最大になるテストケースは、このようなケースではないでしょうか？

16
xa
xb
xc
xd
xe
xf
xg
xh
ax
bx
cx
dx
ex
fx
gx
hx

この場合でもDFSの計算量は、8!=40320で済みそうです。よって、以下のコードでACすることができました。正しいはず。11月から気になってたことが解決しました。ふぅ。小ネタ、平年の2月は8!=40320分（28×24×60）らしいです。 2023-01-11

from collections import defaultdict
N = int(input())
scount = defaultdict(int)
for _ in range(N):
    s = input()
    scount[s[0]+s[-1]] += 1
g = [[1, list(range(1, len(scount)+1))]]
for i, si in enumerate(scount):
    g.append([scount[si], []]) # g[i+1]
    for j, sj in enumerate(scount):
        if si[1] == sj[0]:
            g[i+1][1].append(j+1)
def win(v):
    res = True
    g[v][0] -= 1
    for next in g[v][1]:
        if g[next][0] and win(next):
            res = False
            break
    g[v][0] += 1
    return res
if win(0):
    print('Second')
else:
    print('First')

「再帰関数をできるだけ使うな」という心の声が聞こえてきたので、スタックで書いてみました。勝ち負けをどこに保持するか？とか、あまり考えたくないコードになりました。これに関しては再帰関数のほうがシンプルでいいですね。しかも再帰関数よりちょっと遅くなってしまいました。まあ練習練習。この、ゲームの流れをDFSで調べる処理についても説明します。最初に解いた11月時点ではそれもわかってませんでした。winというのは、その手を選択した人が勝てるかどうか？です。状態が遷移する時、現在の手番の人は、好きな手を選べるので、1つでも勝てる手が存在すれば勝ち局面です。勝てる手が1つ見つかった時点で、他の手を調べる必要はなくなり、枝刈りできます。その場合、1手前の人（相手）にとっては、その手は負ける手であるわけです。これをゲーム終了状態（どちらかが勝った状態）から遡っていき、最初の1手に勝てる手があるかどうかを調べます。 2023-01-11

from collections import defaultdict
N = int(input())
scount = defaultdict(int)
for _ in range(N):
    s = input()
    scount[s[0]+s[-1]] += 1
g = [[1, list(range(1, len(scount)+1))]]
for i, si in enumerate(scount):
    g.append([scount[si], []]) # g[i+1]
    for j, sj in enumerate(scount):
        if si[1] == sj[0]:
            g[i+1][1].append(j+1)
stack = [[-1,True],[0,True]]
while stack:
    cur = stack.pop()
    v = cur[0]
    win = cur[1]
    if v >= 0:
        g[v][0] -= 1
        for next in g[v][1]:
            if g[next][0]:
                stack.extend([[~next,True],[next,True]])
    else:
        g[~v][0] += 1
        if win:
            while len(stack) >= 2 and ~stack[-1][0] == stack[-2][0]:
                stack.pop()
                stack.pop()
            if stack:
                stack[-1][1] = False
if win:
    print('Second')
else:
    print('First')

G - Generalized Subtraction Game

この問題の解説に、Grundy数という初めて聞く言葉が出てきたので、解く前に蟻本の「4-2 ゲームの必勝法を編み出せ！」を読みました。苦労しましたが、なんとか理解して帰ってきました。考え方がクレイジーすぎますね。この問題はほとんどのケースで真似っこ戦略が有効で、真似っこ戦略が使えないケースはGrundy数を使っても計算量が抑えられます。が、Grundy数の勉強のため、全パターン真似っこ戦略を使わずにやりました。対話型の問題は初めてで、デバッグがしにくいなと思いました。TLEが出まくって、やはりPythonだと厳しいか？と疑いましたが、無限ループを入れてしまっていたり、バグ取りに苦労しました。gsetmemoは、1手後の2つの数列長の和が同じ時の、Mexを計算するための遷移先Grundy数のsetをメモするために使っています。ほとんどのケースで高速化に寄与しませんでしたが、速度に大きく影響するケースもあり、gsetmemoを使わないとTLEが2つ出ました。自分の手を決めるために現在の盤面情報が必要なので、リストを作って新しい区間ができたら挿入しようとしていましたが、挿入箇所をbisectでO(log(N))で決めたり、長さが0の時は挿入不要だな～とか、めんどうな処理になるし、リストへの挿入自体O(N)かかるので、このやり方は筋が悪いのですね。おなじO(N)なら全カードの残っているかどうかのリストを用意して、左端のカードのリストと、連続数のリスト、startsとcountsは、自分の手の直前に作り直したほうがわかりやすく、速度も変わらないです。splitmemoというのは、1手進めるときに残った2山の合計枚数と、Grundy数から、2つの山の枚数の例をメモしています。自分の手を決めるときにこれを参照することで、計算せずに正しい手を決められているはずです。あと、Grundy数を使う問題を解くことでXORの性質をいろいろ学びましたね。 2022-11-25

N, L, R = map(int, input().split())
# grundy range 0-N, left 0-(N-L)
idxsm = lambda g_, left_: g_*(N-L+1) + left_
splitmemo = [() for _ in range((N-L+1)*(N+1))]
gsetmemo = [set() for _ in range(N-L+1)]
grundy = [0]*L + [-1]*(N+1-L)
for i in range(L):
    splitmemo[(idxsm(0,i))] = (0,i)
# prepare grundy
for n in range(L, N+1):
    gset = set()
    take_max = min(R, n)
    for take in range(L, take_max+1):
        left = n - take
        gset_left = set()
        if gsetmemo[left]:
            gset_left = gsetmemo[left]
        else:
            for a in range(left+1):
                b = left - a
                if a > b:
                    break
                g = grundy[a] ^ grundy[b]
                splitmemo[idxsm(g,left)] = (a,b)
                gset_left.add(g)
            gsetmemo[left] = gset_left
        gset |= gset_left
    g = 0
    while g in gset:
        g += 1
    splitmemo[idxsm(g,n)] = (0,n)
    grundy[n] = g
# cards remaining
rem = [False] + [True]*(N)
myturn = 1
if grundy[N]:
    print('First', flush=True)
else:
    myturn = 0
    print('Second', flush=True)
while True:
    if myturn:
        xorall = 0
        starts = []
        counts = []
        i = 1
        while i <= N:
            if not rem[i]:
                i += 1
            else: # rem[i]
                starts.append(i)
                while i <= N and rem[i]:
                    i += 1
                # i=N+1 or not rem[i]
                count = i - starts[-1]
                counts.append(count)
                xorall ^= grundy[count]
        # xorall must be > 0
        highbit = 1 << (len(bin(xorall))-3)
        pair_found = False
        for i in range(len(starts)):
            count = counts[i]
            if count < L:
                continue
            if highbit & grundy[counts[i]]:
                gnew = xorall ^ grundy[count]
                for take in range(min(R, count), L-1, -1):
                    left = count - take
                    t = splitmemo[idxsm(gnew,left)]
                    if t: # pair must be found at first trial
                        pair_found = True
                        remove_sta = starts[i] + t[0]
                        print(remove_sta, take, flush=True)
                        for j in range(remove_sta, remove_sta+take):
                            rem[j] = False
                        break
            if pair_found:
                break
        myturn ^= 1
    if not myturn:
        a, b = map(int, input().split())
        if a == b == 0 or a == b == -1:
            break
        for j in range(a, a+b):
            rem[j] = False
        myturn ^= 1

真似っこ戦略を使う場合のコードも載せておきます。基本、これは使うべきです。 2022-11-25

if L != R or not (N^R)&1:
    print('First', flush=True)
    y = R - ((N^R)&1)
    x = 1 + (N-y)//2
    print(x, y, flush=True)
    while True:
        a, b = map(int, input().split())
        if a == b == 0 or a == b == -1:
            break
        print(N-a-b+2, b, flush=True)

AtCoder Beginner Contest 279

2度目の5完！ペナルティは0でした。問題Dで微分を使う必要があり、微分なんて何年も使っていないので、微分の公式を思い出せず、ググらないと計算できませんでした。そのせいで、問題Dだけで30分くらいかかってしまいました。中高生の頃だったら短時間でできたのは間違いなく、くやしい思いをしました。競プロでは、こういった基礎的な数学はとっさに反応できる必要があるんだなと認識しました。問題Eは問題の内容を理解するのに苦労した印象があります。みんなこういう文章を読んでスッと頭に入ってくるんでしょうか？問題の内容を理解したあと、コードを書きながら、これだとTLEだぞ、と思って方針変更し、1回でACできたのは、経験からいろいろ学んだのを感じます。そして、ついに念願の、入緑しました！初めて参加したのがABC266で8/27の開催でした。今日は11/26なのでちょうど3ヶ月です。参加回数10回目で入緑することができました。また、はじめて1000位以内に入れました。AC数履歴は、4,3,3,2,3,4,5,4,4,5でした。 2022-11-26

入緑しました！

F - BOX

コンテスト終了直後は、がんばれば解けたのでは？と思い、終わったあとでやり始めましたが、バグっててACにむちゃくちゃ時間かかりました。それぞれのボールがどの箱に入っているか？を短時間で答えられる構造を作る必要があります。操作タイプ1でYにたくさんボールが入っていると、全ボールの箱情報を書き換えるのが大変なので、どうするかな？という問題ということがわかります。最初なんとなく、同じ箱に入っているボールが同じリストを参照していて、その中に箱が書かれていれば、箱を書き換えられるなぁと考えました。しかし操作のたびにそのリスト自体が増えていってわけがわからなくなります。じゃあリストのリストにするか？などと考えているうちに自動的に深くなっていって、ツリー構造とわかります。そうすると、Union-Findを使えば良いと気づくことができます。same_treeを使わない、uniteするだけのUnion-Findです。これは、使えますね。で、方針変更の疲れにも耐えて書き直したのですが、ACx33、REx39みたいな状況に陥ってしまいました。どこがおかしいかなかなか見つけられず、むちゃくちゃ時間がかかってしまったのですが、じつはQ<Nと勝手に思いこんでしまっており、ボールのサイズを2*Nとしてしまっていたことがわかりました。こういう消耗は時間かかるしつらいなー。 2022-11-27

class Union():
    # 省略
N, Q = map(int, input().split())
box_ball = [i for i in range(N+1)]
ball_box = [i for i in range(N+1)] + [0 for _ in range(Q)]
union = Union(N+Q)
nextball = N
for _ in range(Q):
    q = list(map(int, input().split()))
    if q[0] == 1:
        x = q[1]
        y = q[2]
        if box_ball[y]:
            if box_ball[x]:
                union.unite(box_ball[y], box_ball[x])
            else:
                box_ball[x] = box_ball[y]
            box_ball[y] = 0
            ball_box[union.find_root(box_ball[x])] = x
    elif q[0] == 2:
        nextball += 1
        x = q[1]
        if box_ball[x]:
            union.unite(box_ball[x], nextball)
        else:
            box_ball[x] = nextball
        ball_box[union.find_root(nextball)] = x
    else:
        x = q[1]
        print(ball_box[union.find_root(x)])

G - At Most 2 Colors

こういう動的計画法、解説を理解するのがしんどいです。DPの式から意味を読み取るのがむずかしいので、まず説明の文章だけを読んで、自分でDPの式を組み立てることが多いです。kyopro_friendsさんの解説のDPでやりました。最後のK-1マスが1色の場合と、2色の場合の数をDPで計算していきます。このDPは条件があり、次のマスの色は必ず別の色になる組み合わせをカウントしていきます。そのことによって、直前のK-1マスが1色であれば次の色はC-1色から選べ、直前のK-1マスが2色であれば2色のうちの別の色から選べるので選択肢は1色だけになります。なんとか式を書き上げ、DP[0]からDP[K-1]あたりでミスらないようにコードを書き、ACできました。ACできたものの、問題は、解説を理解することではなく、自分でこの式を導けるか？ということです。動的計画法の問題を見るたび、どうやってこの式にたどりついたんだよ！と思ってしまいます。Kマスが2色である必要があるので、K-1マスまでの状況によって、Kマス目に制限がかかるだろう、というように考えればK-1という数字は自然に出てくるでしょうか？「次のマスの色は必ず変化させて考える」というのは自力で出てきますか？そんなに自然とは思えないですね。でも場合の数を数え上げる場合、加えられる制約は加えたほうが秩序が生まれるようです。DPの問題は、式を作れるかがすべてなので、これまでに出会ったDPの問題をざっと見て、一体どういう思考の流れで式を導き出せているのか？という観点でふりかえってみるのも良いかもしれないです。あ、あとこれ、累積和というやつですね。 2022-11-29

M = 998244353
N, K, C = map(int, input().split())
C = C % M
dp1 = [C]*(N+1)
dp1sum = [0]*(N+1)
for i in range(1, K):
    dp1sum[i] = C * i % M
dp2 = [0]*(N+1)
dp2sum = [0]*(N+1)
dp2sum[2] = dp2[2] = C * (C-1) % M
for i in range(3, K): # if K<=3 do nothing
    js = max(i-K+1, 0)
    je = i - 1
    dp2[i] = (dp1sum[je]-dp1sum[js]) * (C-1) + (dp2sum[je]-dp2sum[js])
    dp2[i] %= M
    dp2sum[i] = dp2sum[i-1] + dp2[i]
    dp2sum[i] %= M
for i in range(K, N+1):
    js = i - K + 1
    je = i - 1
    dp2[i] = (dp1sum[je]-dp1sum[js]) * (C-1) + (dp2sum[je]-dp2sum[js])
    dp2[i] %= M
    dp2sum[i] = dp2sum[i-1] + dp2[i]
    dp2sum[i] %= M
    dp1[i] = C + dp1sum[js] * (C-1) + dp2sum[js]
    dp1[i] %= M
    dp1sum[i] = dp1sum[i-1] + dp1[i]
    dp1sum[i] %= M
print((dp1[N]+dp2[N]) % M)

他の解答を見ていると、むちゃくちゃシンプルなものもありました。嘘みたいにシンプルですが、確かに正しいです。1色と2色のDPを分けておらず、全組み合わせを1つのDPで計算しています。その方が自然ですよね。直前のK-1マスで2色使われていれば、次に使えるのはどちらかなので2色としています。上の解答のように、「次は別の色」という制約は設けていません。自然です。で、K-1マスが1色の場合を考えます。その組み合わせの数はDP[i-(K-1)]なのです。確かに。なんかくやしい。。。その場合、i番目ののマスにはC色使えます。最初の2色使える場合の数はdp[i-1]*2と計算しますが、この中には当然、直前のK-1マスが1色の場合の数x2が含まれてしまっています。K-1マスが1色の場合であるDP[i-(K-1)]*Cから、DP[i-(K-1)]*2を引いておくことで、余計にカウントした分を打ち消すことができます。いや、すごくシンプルだけど、余計にカウントした分を打ち消すところは、美しく、難しいですよね。ひらめきさえすれば、1瞬で解ける可能性もあるのは、おもしろいです。こういうの短時間で解けるようになりたいなぁ。「次使えるのは、同じ2色のうちどっちかだよね。でも最後のK-1マスが1色ならどれ使っても良くなるね。この2つの状況を組み合わせるにはどうすればいいかな？」って考えていくことで、この式にたどり着けるんですかねぇ？ 2022-11-29

M = 998244353
N, K, C = map(int, input().split())
C = C % M
dp = [0]*(N+1)
dp[1] = C
for i in range(2, N+1):
    dp[i] = dp[i-1]*2 + dp[max(i-K+1, 1)]*(C-2)
    dp[i] %= M
print(dp[N])

AtCoder Beginner Contest 280

3度目の5完、そして初めての2連続5完でした。AC数の推移を見ると、順調に成長してることが感じられ、うれしいです。問題Eに70分近く残っていたのですが、勘違いバグをなかなか修正できず、ACできたのは98分くらいでギリギリでした。終了間際は緊張感があり、ACしたときは「ヨッシ！」と叫びました。終了後、問題Fを見ましたが難しく、時間があっても解けなかったであろうことを確認しました。 2022-12-04

E - Critical Hit

終了間際に解けました。どのようなミスをしていたかというと、1と2の合計でN以上になるまでの回数の期待値ということで、2をn2回、1をn1回でN以上となるn2、n1の組み合わせを求めましたが、そのときにまず2をn2回加え、残りは1というような数え方をしてしまっていました。それだと合計N+1で初めてN以上になるパターンが、全部2のときだけになってしまっていました。よく考えたら合計N+1になるのは、N-1になった次に2が出るパターンすべてですね。N-1までは1でも2でもいいのです。貪欲に2ばかりを先に足して残りを1で埋めると、漏れているパターンが大量発生していました。そのことに気づいたのが、残り15分くらいだったでしょうか？では、どのように計算すればよいのか？緊張しながら考え、N-1ちょうどになるときは、次なにが出てもN以上になるので、すべて合算。N-2ちょうどになるときは、次2が出てNになるものだけ合算する。なぜなら、N-2の次に1が出るパターンはN-1のときに、すでに考慮済みです。緊張しながら、なんとか解きましたが、「1と2の合計がN以上になる」というのはいかにも典型的な問題っぽいので、経験を積んだ人は何度も見たことがあり、今回ぼくがやったようなミスでハマったりはしないかもしれません。 2022-12-04

mod = 998244353
N, P = map(int, input().split())

# https://atcoder.jp/contests/abc280/submissions/36995423
# 階乗やchoose省略

ans = 0
inv100 = pow(100, mod-2, mod)
p1 = (100-P) * inv100 % mod
p2 = P * inv100 % mod
n2 = 0
while True:
    # just N-1
    if n2 * 2 > N - 1:
        break
    n1 = N - 1 - n2 * 2
    ans += (n1+n2+1) \
        * pow(p1, n1, mod) * pow(p2, n2, mod) * choose(n1+n2, n2)
    ans %= mod
    n2 += 1
n2 = 0
while True:
    # just N-2
    if n2 * 2 > N - 2:
        break
    n1 = N - 2 - n2 * 2
    ans += (n1+n2+1) \
        * pow(p1, n1, mod) * pow(p2, n2, mod) * p2 * choose(n1+n2, n2)
    ans %= mod
    n2 += 1
print(ans)

F - Pay or Receive

最近5完できるようになってきたので、次のターゲットは6問目の問題Fとなります。が、これは歯が立ちませんでした。AからBに移動するとC増加、BからAに移動するとC減少、という状況を地面の高さに例えるのは、わかりやすくてよいと思いました。「無限アップできる巡回路がない」というのは、「すでに通った頂点に再度到達したときに、高さが一致している」ことです。そうでない場合、回り続けると無限にポイントを増やせます。また、高さの整合性が取れている連結成分内では、XからYにどのように移動しても、ポイントは同じになります。そうでなければ無限アップできてしまうということだからです。よって、問題文に「所持しているポイントの最大値を出力せよ。」と書いてありますが、整合性が取れている連結成分内で移動した場合、いくつかの値の最大値というものは考えられず、確定する1つの値となります。その値は、別の街ZからYに移動したポイント - ZからXに移動したポイントとして、計算することができます。ここで、街Zは任意の街で良いですが、Union-Findのルートを使用しています。Union-Findって便利ですね。何度か使って便利さがわかってきました。 2022-12-04

XとYが同じ連結成分に属しているかどうか？瞬時に判断する必要があるため、Union-Findを使っています。Union-Findにおいて、同じ連結成分である目印は、rootですね。 2023-01-13

N, M, Q = map(int, input().split())
class Union():
    # 省略
u = Union(N+1)
g = [[] for _ in range(N+1)]
infinite_loop = set()
INF = 10**16
costs = [INF]*(N+1)
for _ in range(M):
    a, b, c = map(int, input().split())
    u.unite(a, b)
    g[a].append((b, c))
    g[b].append((a, -c))
for v in range(1, N+1):
    if u.find_root(v) == v: # find_root is cheap
        stack = [v]
        costs[v] = 0
        inf_found = False
        while stack:
            cur = stack.pop()
            for next, c in g[cur]:
                if costs[next] == INF:
                    costs[next] = costs[cur] + c
                    stack.append(next)
                else:
                    if costs[next] != costs[cur] + c:
                        infinite_loop.add(v)
                        inf_found = True
                        break
            if inf_found:
                break
for _ in range(Q):
    x, y = map(int, input().split())
    if u.find_root(x) != u.find_root(y):
        print('nan')
    elif u.find_root(x) in infinite_loop:
        print('inf')
    else:
        print(costs[y]-costs[x])

G - Do Use Hexagon Grid 2

この問題はぼくにとってかなり難しく、ACに数日かかりました。ようやく理解して提出し、多くのケースでACできたあとも、random_07.txtとrandom_15.txtの2つのケースがTLEとなって、苦労しました。最終的になんとかACした処理時間は2929msでした。この問題に関して、自力で考えられたことと言えば、1次元の場合は何通りかな？ということくらいです。まあこの考察は当然必要なのですが、2次元、3次元と次元が増えたときにどのように計算すればいいのか簡単に思いつきませんでした。1次元の場合は、左から小さい順に並んでいるとすると、一番左のマスに注目して、距離D以下のマスが右にn個あれば、n個を選ぶか選ばないかの組み合わせで、2^n通りとし、すべてのマスについて合計すればいいでしょう。一番左のマスを必ず含むようにすれば、排他的な組み合わせを作っていくことができるからです。ではこれが2次元になった場合はどうするのか？混乱して整理しきれませんでした。2次元目についても一番左を必ず選ぶことで排他的な組み合わせを作っていけばいいです。一番左に複数のマスがあったらどう処理すればいいのか？とか考えていると混乱してしまうのですが、複数あっても気にせず処理できます。まずy=YからY+Dまでで組み合わせを数え、Y+1からY+Dまでの組み合わせを数えて引けばシンプルです。このようにすれば、y=Yのマスを含む組み合わせの数だけを抽出でき、つぎはy=Y+1以上を調べるので排他的に調べることができます。3次元目も同様です。ようやくこの方針でプログラムを書いて提出したのですが、上記の通りTLEx2でした。その後も苦労し、最終的にはYからY+DのマスのリストとY+1からY+Dのマスのリストをそれぞれ0から1つずつappendして作っていたところ、YからY+DのマスのリストはY+1からY+Dのマスのリストに、y=Yのマスのリストをextendして作る、というように変更することでリストのappendなどの処理を減らしてACできました。時間はギリギリでした。YとY+Dをスライドさせていくことになるので、dequeで後ろに追加して前を消してく方法なども考えましたが、範囲のマスを抽出したあとで次の次元でソートして、ということを3次元目まで繰り返しているので、dequeからリストを新しく作って次の次元に渡すことになり、高速になりませんでした。これまでも経験則として書いてますが、Pythonはリストが増えると遅いです。この問題では6角格子（Hexagon Grid）のマスとマスの距離が必要ですが、max(|x|, |y|, |x-y|)で求められるようです。自分では導けていませんでしたが、確かにそうです。(x,y)->(x,y,x-y)と座標変換することで、距離D以下というのは2つのマスが1辺の長さがDの立方体の中に入っていることと同値になります。また、2つの点の各座標の差の最大値を「チェビシェフ距離」というようです。現時点でぼく以外のPythonでのACは7名で、黄色とオレンジの方しかいません。8人目のぼくだけ緑です。問題Gで、PythonでのACが8人しかいない上に、ぼく以外黄色以上なのを見ると、やっぱこの問題むずかしいんだよね。自分はがんばってるなぁ、と思えます。笑。 2022-12-07

MOD = 998244353
pow2 = [0]*301
pow2[0] = 1
for i in range(1, 301):
    pow2[i] = pow2[i-1] * 2 % MOD
N, D = map(int, input().split())
xyz = []
for _ in range(N):
    x, y = map(int, input().split())
    xyz.append((x, y, x-y))
def count_yrange(zs):
    zs.sort()
    lenzs = len(zs)
    ret = 0
    for i in range(lenzs):
        z = zs[i]
        ze = z + D
        j = i
        while j < lenzs and zs[j] <= ze:
            j += 1
        ret = (ret + pow2[j-i-1]) % MOD
    return ret
def count_xrange(yz):
    yz.sort(key=lambda item:item[0])
    lenyz = len(yz)
    ret = 0
    i = 0
    while True:
        if i == lenyz:
            break
        y = yz[i][0]
        ye = y + D
        zs = []
        zs1 = []
        j = i
        while j < lenyz and yz[j][0] == y:
            zs.append(yz[j][1])
            j += 1
        i = j
        while j < lenyz and yz[j][0] <= ye:
            zs1.append(yz[j][1])
            j += 1
        cy1 = count_yrange(zs1)
        zs1.extend(zs)
        cy = count_yrange(zs1)
        ret = (ret + cy - cy1) % MOD
    return ret
xyz.sort(key=lambda item:item[0])
ans = 0
i = 0
while True:
    if i == N:
        break
    x = xyz[i][0]
    xe = x + D
    yz = []
    yz1 = []
    j = i
    while j < N and xyz[j][0] == x:
        yz.append((xyz[j][1], xyz[j][2]))
        j += 1
    i = j
    while j < N and xyz[j][0] <= xe:
        yz1.append((xyz[j][1], xyz[j][2]))
        j += 1
    cx1 = count_xrange(yz1)
    yz1.extend(yz)
    cx = count_xrange(yz1)
    ans = (ans + cx - cx1) % MOD
print(ans)

この問題を解くにあたり、処理が複雑すぎてなかなか進められず参っていた間、別の楽な方法がないか逃げていた時間があって、その時に新しいグラフの用語を覚えました。最大300マスなので、すべての2つのマス間の距離を計算できます。よって、距離がD以下のマス間をエッジを結んでグラフを作って解く方法があるのではないか？と考えました。「選んだマスのうちどの2マスの距離もD以下になる」ことは「どの頂点間にもエッジがある」と言い換えられます。「どの頂点間にもエッジがある」グラフのことを完全グラフというようです。知りませんでした。そして完全グラフである誘導部分グラフ（あるグラフから、一部の頂点を取り出し、その頂点対の辺の有無が元のグラフと一致するグラフ）のことを、クリーク（clique）と言います。するとこの問題は、クリークの数を求める問題と言い換えられることがわかります。NetworkXにfind_cliquesという関数があり、最大クリークを得ることができることを知りました。これを使って、クリーク数を求められないか？考えてみましたが、断念しました。グラフとグラフの積をいろんな最大クリーク間で何重にも求めなければいけないような処理になりそうでした。グラフの問題として解く方法はあるのでしょうか？以下はfind_cliquesだけ呼んで終了するコードです。Python (3.8.2)で、ここまでの処理時間は2154msでした。 2022-12-07

import sys
import networkx as nx
g = nx.Graph()
N, D = map(int, input().split())
nodes = []
for _ in range(N):
    x, y = map(int, input().split())
    nodes.append((x, y))
for i in range(N-1):
    x1, y1 = nodes[i]
    for j in range(i+1, N):
        x2, y2 = nodes[j]
        dx = x2 - x1
        dy = y2 - y1
        if max(abs(dx), abs(dy), abs(dy-dx)) <= D:
            g.add_edge(i, j)
for i in nx.find_cliques(g):
    pass
sys.exit()

AtCoder Beginner Contest 281

4完でした。問題Bでトラブって15分経ちました。問題DはDPでしたが、自分にとってはまだ難しい部類で、終わった時点で80分。これを解ききれたことは喜びたいと思います。問題Eを少しやり始めて、プライオリティキュー使ったらできるでしょと思いながらコンテスト終了しましたが、実際にACできたのは翌日でした。このようなプライオリティキューの使い方を頭に入れられたので良い勉強になったと思います。前回まで2連続5完していましたので、4完に減ると残念ですが、内容をふりかえると実力だったと納得できました。問題Bと問題Dで、デバッグ時のprintを残して提出してしまい、それぞれ1ペナルティ食らったのはもったいないので、今後、気をつけたいです。Ratingはかろうじて上昇しました。

B - Sandwich Number

罠にハマってしまいました。読み込みの高速化でinput = sys.stdin.readlineとすることを最近覚えました。副作用はないと思っていたのですが、stdin.readlineだと終端文字が取れるようです。8文字の入力なのにlenを取ると9が返ってきて、なんだこれは？と思っているうちに時間が経ってしまいました。意味もなく使わないようにしたいと思います。入力をsplitする場合は問題なさそうですが。 2022-12-10

D - Max Multiple

コンテスト中にACできましたが、ぼくにとっては結構難しいと感じます。最近5問解けることも出てきて、4完で終わると残念に感じてしまいますが、この4問目がコンテスト中に解けたことは喜ばしいことで、満足したいです。最初からDPと思わず、全く解ける気がしないと感じましたが、「あれ？DPでいけるのか？」と気づいて頭が働き始めました。DPは、できる気がしないような問題が解けてしまうところがあり、いまだにマジックのような感じがしています。そのロジックを自分で組み立てられるのですから、これが解けることは、大きな喜びです。これまでに選択した個数と、Dで割った余りごとに最大値を計算していけばよいです。aiを選択すると個数が1つ増え、Dで割った余りも計算することができます。初期状態は0個、余り0の状態で、最大値が0のみです。存在しない状態から次の状態に遷移してはいけないので、他の初期値を-1としておき、-1でない値が入っていたときだけ、次の状態を計算するようにします。最初存在しない状態を別扱いできておらず、デバッグにも時間を使ってしまい、この問題が解けたのは、開始から80分くらいでした。 2022-12-10

N, K, D = map(int, input().split())
alist = [0] + list(map(int, input().split()))
idx = lambda m,p:p*(K+1)+m # m ko, amari p
dp = [[-1]*((K+1)*D) for _ in range(N+1)]
dp[0][idx(0,0)] = 0
for i in range(N): # i -> i+1
    for j in range((K+1)*D):
        dp[i+1][j] = dp[i][j]
    for m in range(min(i+1,K)):
        for p in range(D):
            if dp[i][idx(m,p)] != -1:
                nextval = dp[i][idx(m,p)] + alist[i+1]
                dp[i+1][idx(m+1,(p+alist[i+1])%D)] \
                    = max(dp[i+1][idx(m+1,(p+alist[i+1])%D)], nextval)
print(dp[N][idx(K,0)])

E - Least Elements

昇順で最初のK個と残りのM-K個をそれぞれ別管理し、スライドさせていったときに消すものと追加するものだけ処理していけば良いな、K個の最大とM-K個の最小の値が必要になるので、プライオリティキューでやれば良いかな？というところまでは、コンテスト時間内に思っていました。終了後に、それでできるだろーと思ってやっていましたが、かなり苦労しました。その苦労は、プライオリティキューの使い方に慣れておらず、整理できずに混乱したのが原因と思っています。03_m_small_00.txtだけREという状態がしばらく続きましたが、プライオリティキューの先頭にアクセスするときに存在確認しておらず、不正アクセスしていたことが原因でした。これは基本でしょう。そして、プライオリティキューは先頭のpopしかできないので、他の要素を削除するときはremovedフラグを別途用意して維持する必要があります。削除するときは先頭であればpopし、先頭をpopしたあとは、removedである限りpopし続けることによって、先頭はremovedではない状態を維持する必要があるでしょう。プライオリティキューは先頭が大事ですから。removedが先頭に残っていてはいけません。また、存在確認も必要でしたので、setを使いました。pushしたとき、remvoedフラグを更新したときは、必ずsetも更新します。ということで、プライオリティキューを使いますが、補助的にremovedフラグのリストと要素setをあわせて使う必要がありました。このような使い方はよくあるだろうと思いますので、この問題を通して学んだことで、今後混乱せずに使うことができるようになったのではないかと思います。 2022-12-11

復習です。小さい方K個と大きい方M-K個のIDのsetを持っておいて、とりあえず消すものは消します。setからは消せるが、heapqからは消せないので、removedリストで管理しておく必要があります。heapqから消さないというのは直感的ではないですが、removedリストを見ればすでに消えているかどうかはわかるので、これを自然にやれるようになるべきでしょう。問題は追加するときに、大きさの整合性が取れている必要があること。これはheapqを使って境界を確認し、整合性が取れる方に追加する必要があります。K個のグループのmax値以下なら、K個のグループに追加するということで良いでしょう。消したグループに追加したなら、そのままでOK。異なるグループに追加した場合は、数をK個とM-K個になるように、1つ移動して調整しなければなりません。このときも最大値、もしくは最小値に相当するものをheapqの先頭を確認して移動すれば良いです。setとremovedリストはやはり必要だということを確認しました。 2023-01-12

import heapq
N, M, K = map(int, input().split())
alist = list(map(int, input().split()))
_m = [(alist[i], i) for i in range(M)] # val, idx
_m.sort(key = lambda x:x[0])
_k = [(-_k[i][0], _k[i][1]) for i in range(K)]
big = _m[K:M]
heapq.heapify(_k)
heapq.heapify(big)
kidset = {x[1] for x in _k}
bigidset = {x[1] for x in big}
ans = sum([-x[0] for x in _k])
anss = [ans]
l = 0
r = M
removed = [False]*N
while r < N:
    minus = alist[l]
    plus = alist[r]
    remove_from_k = True
    removed[l] = True
    # remove
    if l in bigidset:
        bigidset.remove(l)
        remove_from_k = False
        if big[0][1] == l:
            heapq.heappop(big)
            while big and removed[big[0][1]]:
                heapq.heappop(big)
    else:
        kidset.remove(l)
        ans -= minus
        if _k[0][1] == l:
            heapq.heappop(_k)
            while _k and removed[_k[0][1]]:
                heapq.heappop(_k)
    # add
    if not _k or plus <= -_k[0][0]: # check _k empty at first!
        # add to _k
        kidset.add(r)
        ans += plus
        heapq.heappush(_k, (-plus, r))
        if not remove_from_k:
            # removed from big
            # need to move from _k to big
            while True:
                hoge = heapq.heappop(_k)
                if not removed[hoge[1]]:
                    ans -= -hoge[0]
                    kidset.remove(hoge[1])
                    while _k and removed[_k[0][1]]:
                        heapq.heappop(_k)
                    bigidset.add(hoge[1])
                    heapq.heappush(big, (-hoge[0], hoge[1]))
                    break
    else:
        # add to big
        bigidset.add(r)
        heapq.heappush(big, (plus, r))
        if remove_from_k:
            # removed from _k
            # need to move from big to _k
            while True:
                hoge = heapq.heappop(big)
                if not removed[hoge[1]]:
                    ans += hoge[0]
                    bigidset.remove(hoge[1])
                    while big and removed[big[0][1]]:
                        heapq.heappop(big)
                    kidset.add(hoge[1])
                    heapq.heappush(_k, (-hoge[0], hoge[1]))
                    break
    anss.append(ans)
    l += 1
    r += 1
print(*anss)

F - Xor Minimization

この問題は、初めて自力で解けた6問目となり、成長を感じられてうれしいです。わりと早い段階でこうやればいいなぁということは思いついたのですが、1発ではサンプルケースがうまくいかず、minimax関数の戻り値のところの細かい処理など、修正してのACとなりました。 なんかGrundy数を勉強してからXOR好きですね。 2022-12-11

import sys
input = sys.stdin.readline
N = int(input())
alist = list(map(int, input().split()))
alist.sort()
inf = alist[-1] + 1
# return possible minimum of max
def minimax(bitmask, s, e):
    '''s != e'''
    if bitmask == 1:
        if bitmask & alist[s] == bitmask & alist[e-1]:
            return 0
        else:
            return 1
    i = s
    while i != e and bitmask & alist[i] == 0:
        i += 1
    res = inf
    if s != i:
        res = min(res, minimax(bitmask>>1, s, i))
    if i != e:
        res = min(res, minimax(bitmask>>1, i, e))
    if s == i or i == e:
        return res
    return bitmask + res
topbit = 1 << len(bin(alist[-1]))-3
print(minimax(topbit, 0, N))

G - Farthest City

DPに持ち込むのだろうと思いながら、持ち込めず解説を見ました。問題Gを初めて自力で解けるのはいつになるのでしょうか？条件を満たすグラフをどのように作るかまでは、自分で導くことができました。そこはうれしいです。そして総数を求める式も作れるなぁと思い、でも1から同じ距離の頂点グループの組み合わせが膨大にあり過ぎて計算できないなぁと思い、よってDPでなんとかするんだろうなぁ、というところまで考えましたが、力尽きて解説を見ました。DPに持ち込めることがすごく大事ですね。今までいろいろなDPの問題を解いてきたので、考え方のノウハウを抽出したいです。実行時間が3286msと遅めなのですが、改善の余地があるのかはちょっとわからないです。Combinationを計算しているところは左右対称なので無駄ですが、これは大した計算ではないです。 2022-12-12

N, M = map(int, input().split())
combi = [[1]*(i+1) for i in range(N-1)]
for i in range(1, N-1): # max N-2 is necessary
    for j in range(1, i):
        combi[i][j] = (combi[i-1][j-1] + combi[i-1][j]) % M
    combi[i][-1] = 1
pow2 = [1]*(N*N)
for i in range(1, N*N):
    pow2[i] = pow2[i-1] * 2 % M
dp = [[0]*(N-1) for _ in range(N-1)]
# init
for i in range(1, N-1):
    dp[i][i] = combi[N-2][i] * pow2[i*(i-1)//2] % M
for i in range(1, N-1): # used i
    for j in range(1, i+1): # prev group
        pow2_j_1 = pow2[j] - 1
        pow2_j_1_pow_k = 1
        for k in range(1, N-1-i): # next group
            pow2_j_1_pow_k = pow2_j_1_pow_k * pow2_j_1 % M
            count = dp[i][j] * combi[N-2-i][k] \
                * pow2_j_1_pow_k * pow2[k*(k-1)//2] % M
            dp[i+k][k] = (dp[i+k][k] + count) % M
ans = 0
for j in range(1, N-1):
    ans = (ans + dp[N-2][j] * (pow2[j] - 1)) % M
print(ans)

AtCoder Beginner Contest 282

くやしい結果となりました。何度か5問解けたことで、力がついてきた気がしていたのですが、今回は、極めてシンプルな、3問目の問題CでTLEに陥りました。しかし、何がまずいのかピンとこず、一旦スキップして問題Dに進んだのですが、問題Cが解けなかったことで動揺していてうまくいきませんでした。考え方がわかったにも関わらず、落ち着いてバグを直せませんでした。なによりも問題Cでつまずいたことがショックで、終わったあと、かなりイライラしてしまいました。連続で参加して疲れているし、休めばよかったかなぁとも後悔しましたが、失敗したからこそ、学ぶことが多かったとも、言えそうです。これがCやC++を使っていく転機にもなりえます。

Rating ダウン

ここに来て順位が過去最低。そして、問題Cを99:59にACするという奇跡w

99:59でAC！

C - String Delimiter

※最初に書きます。この問題でTLEを出してイライラしていましたが、解決しました。PEP 8 Programming Recommendationsにこのことが書かれています。

Code should be written in a way that does not disadvantage other implementations of Python (PyPy, Jython, IronPython, Cython, Psyco, and such).
For example, do not rely on CPython’s efficient implementation of in-place string concatenation for statements in the form a += b or a = a + b. This optimization is fragile even in CPython (it only works for some types) and isn’t present at all in implementations that don’t use refcounting. In performance sensitive parts of the library, the ''.join() form should be used instead. This will ensure that concatenation occurs in linear time across various implementations.

https://peps.python.org/pep-0008/#programming-recommendations

いや、まさに。performance sensitiveなところで、文字結合に+=じゃなくて''.join()を使えと。これ常識なんですかね。Pythonを使うなら、知っておかなければならない常識なのでしょう。こういうの知らずに失敗するのは、くやしいですね。 2022-12-20

この問題Cが、ABC282の重大問題でした。わからないことも多いので、事実を書きます。以下のコード、PyPy3 (7.3.0)でACx6、TLEx14となります。最初に提出したのはこのようなコードでした。01_test_04.txtから01_test_17.txtまで全部TLE、2秒超えです！これで動揺しまくって問題Cをスキップし、落ち着かないまま問題Dにいって、惨敗のきっかけとなりました。

N = int(input())
outer = 1
ans = ''
for c in input():
    if c == '"':
        outer ^= 1
    if outer and c == ',':
        c = '.'
    ans += c
print(ans)

今このnoteを書いてる途中で気づいたのですが、同じコードがPython (3.8.2)で、74ms！ACできてしまいます。Pythonの方が圧倒的に速いのかよ！イラつかせるなぁ。なぜ気づいたかというと、自分のマシン上で、この問題の調査のために以下のコードを実行すると0.1秒で終了しました。自分のローカル環境はPyPyではなく、Pythonなのです。PyPy、2秒超えるってどういうことだよ。ふざけんな。

import time
time_sta = time.time()
s = ''
for _ in range(1000000):
    s += 'a'
print(time.time()- time_sta)

もう1つ気になることは、リストに1文字ずつappendしておいて、最後にjoinすると、速いのです。ふざけんな。このコードがPyPyで86ms！なんでやねん！てあれ？Pythonで63ms！これもPythonの方が速いのかよ！PyPyざけんな。しかし公式解説がなぜかPythonで、しれっとjoinを使って実装しているのです。正直""の内外判定はどうでもよく、なぜjoinで実装しているのか？を書くべきではないかとモヤモヤする解説です。

N = int(input())
outer = 1
ans = []
for c in input():
    if c == '"':
        outer ^= 1
    if outer and c == ',':
        c = '.'
    ans.append(c)
print(''.join(ans))

ちなみに、このC言語のコードで実行時間4msを出すことができ、全提出の4位に入ることができ、少し溜飲を下げることができました。3ms1人、4ms3人です。いや、普通インデックスで指定してダイレクトに書き換えますよね。Pythonではこれができない。TypeError: 'str' object does not support item assignment.というエラーが出ます。なんでやねん。今後2度と、速度問題でロジックと無関係なところで苦労し、ストレスを感じたくありません。簡単な問題ではC言語も使えたら、爆速実行時間をたたき出し、溜飲を下げられる可能性があります。今後のために準備しておきたいです。この問題は、C、C++を取り入れるきっかけになるのでしょうか？だとしたら、あとでふりかえって良かったと思える日が来るかもしれません。 2022-12-19

Submission #37370216 - HHKB Programming Contest 2022 Winter(AtCoder Beginner Contest 282)

D - Make Bipartite 2

コンテスト時間内に解答したかったですが、バグをとれませんでした。問題Cで動揺していたせいでしょうか？コンテスト終了後に落ち着いてやり直してもTLEとなり、連結成分間の辺の数を全連結成分ペアに対してかけ算で計算していたことで、計算量がO(N^2)になってしまっていたことが原因でした。不覚です。N頂点全体の最大エッジ数N(N-1)/2から、2部グラフが崩れるエッジ数、すなわち同一連結成分内の同じグループの頂点間のエッジ数と、はじめからあるエッジ数Mを引くことで、ぼくがやってしまったようなO(N^2)の計算を回避しつつ、答えを得ることができます。気づけずくやしいです。DFSで連結成分を抽出する処理もなんか落ち着いて実装できず、最初バグだらけになってました。usedフラグやcolorリストを更新するのは、stackからpopするときか、appendするときか？といったこともブレブレで、反省です。ABC282、ダメダメです。 2022-12-17

import sys
N, M = map(int, input().split())
g = [[] for _ in range(N)]
for _ in range(M):
    u, v = map(int, input().split())
    g[u-1].append(v-1)
    g[v-1].append(u-1)
used = [False]*N
color = [-1]*N
ans = N*(N-1)//2 - M
for v in range(N):
    if used[v]:
        continue
    stack = [(v,0)] # color 0
    used[v] = True
    color[v] = 0
    countcol = [0,0]
    while stack:
        cur = stack.pop()
        curv = cur[0]
        curc = cur[1]
        colnext = curc^1
        countcol[curc] += 1
        for next in g[curv]:
            if used[next]:
                if color[next] != colnext:
                    print(0)
                    sys.exit()
                continue
            used[next] = True
            color[next] = colnext
            stack.append((next,colnext))
    for count in countcol:
        if count > 1:
            ans -= count*(count-1)//2
print(ans)

E - Choose Two and Eat One

ボール数が500なので、全ボール間の得点を計算し、完全木を作れます。このように考えました。頂点の辺の重みの最大値でソートし、それが小さい順に消していけばいいのでは？と。最大が最小であれば、その頂点を消しても他の頂点に対する、より重みの大きな辺を残すことができるはずだからです。辺の重みの最大値が一致していて、その辺を共有している2頂点の場合は、2番目に大きな重みが大きい方を後で消すようにします。と考えてましたが、行き詰まって解説を見ると、最大全域木を求めればよいとのことです。2つのボールを選ぶ操作は、1本の辺を選ぶことと同値です。1つずつ頂点を消すので、連結成分の中で残っている点は常に1つだけであり、閉路をつくることは不可能です。つまり、この操作はどのような順序であっても、全域木を作る操作に等しいです。であれば、最大全域木の合計得点が答えです。こういうの、気づきたいものです。 2022-12-18

class Union():
    # 省略
N, M = map(int, input().split())
alist = list(map(int, input().split()))
es = []
for i in range(N-1):
    for j in range(i+1, N):
        es.append(((pow(alist[i],alist[j],M)+pow(alist[j],alist[i],M))%M,i,j))
es.sort(key=lambda e:-e[0])
u = Union(N)
ans = 0
for e in es:
    if not u.same_tree(e[1], e[2]):
        u.unite(e[1], e[2])
        ans += e[0]
print(ans)

F - Union of Two Sets

Sparse Tableそのものとのことでした。Sparse Tableを知りませんが、意味するところがわかれば、すぐにコードを書くことはできます。任意区間を、2つの2べき幅の区間の和でカバーできるという発想です。気づける人は気づけるかもしれません。 2022-12-18

import math
N = int(input())
maxdouble = math.floor(math.log2(N))
leftidx = []
count = 0
lrs = []
for i in range(maxdouble+1):
    leftidx.append(count+1)
    width = 2**i-1 # r-l
    lrs.extend([(l,l+width) for l in range(1, N-width+1)])
    count += N - width
print(count, flush=True)
for lr in lrs:
    print(*lr, flush=True)
Q = int(input())
for _ in range(Q):
    L, R = map(int, input().split())
    log2LR = math.floor(math.log2(R-L+1))
    l = leftidx[log2LR] + L - 1
    r = leftidx[log2LR] + R - 2**log2LR
    print(l, r, flush=True)

G - Similar Permutation

解説にEDPC T - Permutationが参考になるとあったので、まずそちらをやりました。EDPC T、理解するのに苦労しました。すごい問題です。そしてこの問題に戻ってきても、同じ考え方であると納得するのに時間がかかりました。1からiまでの並べ替えで、もとの昇順の数列(1,2,3,4,….,N)内での前後関係を表現しており、その発想はクレイジーだと思いました。途中の段階で実際にどの数字が割り当てられるのかわからず、Nまで挿入して初めて実際の数字が決まることが、理解するのに時間がかかる原因かなぁと思っています。使った数字の個数、類似度、Aの最後の挿入位置、Bの最後の挿入位置、という4次元のDPになります。4次元は初めてです。紙に描いて考え、なんとか遷移の処理を整理し、ACすることができました。2次元累積和の計算も、ぼくは初めてでした。どのように計算するべきか考える機会を得られたのは良かったです。数列Aで、0からi-1までの数字を挿入済で、最後に挿入したi-1が[j]の位置にあるとき、iを、[0]から[j]までの位置に挿入すれば[i]<[i-1]、[j+1]から[i]までの位置に挿入すれば[i]>[i-1]となります。Bの<>と一致するには…という風に考えていくと、どのような累積和を計算する必要があるのか、整理することができます。O(100^4)になるので、TLEしないか不安になりますが、遷移処理を高速化すればいけましたね。このコードは1080msで、現時点でPythonの中で2番目の処理速度が出ていました！しかしコンテスト時間内にここまで整理して、ちゃんと実装できる気がしないです。120人も解いてるの半端ないです。。 2022-12-19

考えているときに描いたメモ

N, K, P = map(int, input().split())
dp = [[1]] # dp is list of matrix
for i in range(1, N): # previously inserted i numbers
    ni = i + 1 # i -> ni
    kmax = min(ni-1, K) # max similarity to calculate next
    ni2 = ni*ni
    dp_next = [[0]*(ni2) for _ in range(kmax+1)] 
    for j, mtx in enumerate(dp):
        tempsum = [0]*(i*i)
        cur = 0
        for x in range(i): # right dir tempsum
            xi = x*i
            tempsum[xi] = mtx[xi]
            for y in range(1, i):
                tempsum[xi+y] = tempsum[xi+y-1] + mtx[xi+y]
                tempsum[xi+y] %= P
        mtx_next = dp_next[j]
        for x in range(i): # up dir
            memo = 0
            idx = i * (i-1) + x
            idxnext = ni * (i-1) + x + 1
            for _ in range(i):
                memo += tempsum[idx]
                mtx_next[idxnext] += memo
                mtx_next[idxnext] %= P
                idx -= i
                idxnext -= ni
        if j + 1 <= K:
            mtx_next = dp_next[j+1]
            for x in range(i): # down dir
                memo = 0
                idx = x
                idxnext = ni + x + 1
                for _ in range(i):
                    memo += tempsum[idx]
                    mtx_next[idxnext] += memo
                    mtx_next[idxnext] %= P
                    idx += i
                    idxnext += ni
        for x in range(i): # left dir tempsum
            xi = x*i
            tempsum[xi+i-1] = mtx[xi+i-1]
            for y in range(i-2, -1, -1):
                tempsum[xi+y] = tempsum[xi+y+1] + mtx[xi+y]
                tempsum[xi+y] %= P
        mtx_next = dp_next[j]
        for x in range(i): # down dir
            memo = 0
            idx = x
            idxnext = ni + x
            for _ in range(i):
                memo += tempsum[idx]
                mtx_next[idxnext] += memo
                mtx_next[idxnext] %= P
                idx += i
                idxnext += ni
        if j + 1 <= K:
            mtx_next = dp_next[j+1]
            for x in range(i): # up dir
                memo = 0
                idx = i * (i-1) + x
                idxnext = ni * (i-1) + x
                for _ in range(i):
                    memo += tempsum[idx]
                    mtx_next[idxnext] += memo
                    mtx_next[idxnext] %= P
                    idx -= i
                    idxnext -= ni
    dp = dp_next
print(sum(dp[K]) % P)

上と同じコードを、C言語で書いてみました。Pythonとは違って配列とか最大サイズで全確保してます。上のPythonが1080ms、このC言語が1352msでした。ACはできて良かったですが、むちゃくちゃ速くなってしまうことをどこかで期待してましたが、そうはいきませんでした。言語ごとの特徴とらえて高速化必要ですね。 2022-12-21

Submission #37413777 - HHKB Programming Contest 2022 Winter(AtCoder Beginner Contest 282)

Ex - Min + Sum

1ヶ月前にやったABC277以来のExです。しばらくExは時間がかかるので見ないようにし、参加したABCのGまでを埋め続けていましたが、そちらは完了したので、この問題をなんとなく見始めました。自力で考えたことはというと、ある区間内では、Aの最小値は動かないので、まず区間とAの最小値を固定し、lとrでそれをはさみこむような（つまり、そのようにl,rを選べば、Aの最小値は変化しない）組み合わせを数えれば良いかなぁということでした。l,rの2次元グラフを描きました。l<=rなので、直角二等辺三角形の領域となります。Aの最小値のインデックスをmとすると、上記方針でl<=m、m<=rの長方形部分を調べることができ、その長方形を消すと、2つの小さい直角二等辺三角形が残ります。残った三角形に対して再帰的に数えていけばよいです。しかし、残った区間のAの最小値のインデックスを高速に求める方法がわからず、諦めました。よくあるように、最後のピースが足りないですが、まあここまで考えられたのはうれしいです。Cartesian treeという構造を使うことで、残った区間のAの最小値のインデックスは、グラフをたどるだけで得られることがわかりました。Cartesian treeを作るのは、テキトーにやろうとするとコストが高そうですが、O(N)で求めることができます。これは驚きでしたし、Cartesian tree構築の短いプログラムを、なぜこれでいいのか理解するのは苦労しました。で、Cartesian treeを構築したあとも2つ苦労しまして、1つはBの右端を[m,r]内でループしながら、条件を満たすBの左端を求める部分です。if r-m >= m-l:のelse:のところがそれにあたりますが、ifの方の、左から調べるコードよりちょっとややこしくなってしまっています。累積和のリストが与えられて、右から左に合計値maxsum以下になる左端を求めるの、混乱します。もう1つ苦労したのは、いつものようにTLEです。テストケース013.txtのTLEがなかなか取れませんでした。最初再帰呼び出しを使って実装して2秒の制限を超えていたのですが、スタックを使うように変更することで処理時間が513msとなってACすることができました。再帰呼び出しとえらい違いです。再帰呼び出しは遅いので要注意ですね。 2022-12-24

import sys
input = sys.stdin.readline
import bisect
N, S = map(int, input().split())
alist = [0] + list(map(int, input().split()))
cartesian_tree = [[] for _ in range(N+1)]
parent = [-1 for _ in range(N+1)]
stack = []
for i in range(1, N+1):
    prev = -1
    while stack and alist[i] < alist[stack[-1]]:
        prev = stack.pop()
    if prev != -1:
        parent[prev] = i
    if stack:
        parent[i] = stack[-1]
    stack.append(i)
root = -1
for i in range(1, N+1):
    if parent[i] != -1:
        cartesian_tree[parent[i]].append(i)
    else:
        root = i
bsum = [0]
for b in map(int, input().split()):
    bsum.append(bsum[-1] + b)
stack = [(1, N, root)]
count = 0
while stack:
    l, r, m = stack.pop()
    maxsum = S - alist[m]
    if r-m >= m-l:
        for i in range(l, m+1):
            maxidx = bisect.bisect_right(bsum, bsum[i-1] + maxsum)
            if maxidx > m:
                count += min(r+1, maxidx) - m
    else:
        for i in range(m, r+1):
            target = bsum[i] - maxsum
            minidx = bisect.bisect_right(bsum, target)
            if bsum[minidx-1] < target:
                minidx += 1
            if minidx <= m:
                count += m + 1 - max(l, minidx)
    for i in cartesian_tree[m]:
        if i < m:
            stack.append((l, m-1, i))
        else:
            stack.append((m+1, r, i))
print(count)

AtCoder Beginner Contest 283

クリスマスイブ、4完でした。問題Eの時点で1時間残っており、30分くらいでわかった！と思って提出したのですが、最後までWAx12が取れませんでした。なにがおかしいのか？コンテスト時間中に全く気づけないという状況で、完敗です。Ratingもほぼ横ばいでした。大晦日はないので、年内最後ですよね…。連続で参加し続けて疲れており、そろそろ休みたかったのでうれしいです。

E - Don't Isolate Elements

最初の方針はこうです。1行目に孤立要素があるか調べる、なければ、そのまま2行目に進む、1行目に孤立要素があったら2行目を反転、1行目の孤立要素がなくなったら2行目に進む…、これをN-1行目まで続けて、最後にN行目に孤立要素がなければOK。これでいいと思いこんでしまい、サンプルは正解しましたが、提出結果はACx18、WAx12でした。コンテスト時間中になにがおかしいのか全く気づきませんでした。まだまだダメダメだぁという感想しかありません。どこが間違っていたかというと、「そのまま2行目に進む」って書いてるところですね。2行目を反転させてもさせなくても1行目に孤立要素がない場合もあり、その場合は両方のパターンを考慮する必要がありました。なので、i行目まで確定した時点で、i-1行目と、i行目を反転させたかどうかで、(0,0),(0,1),(1,0),(1,1)の4通りのパターンそれぞれである場合の操作回数の最小値を更新する、DPで解く必要があります。i行目に孤立要素があるかどうかは、i-1行目の状態に影響を受けるためです。というわけで「できた！」と思ったのは完全に勘違いで、あらためてやり直してみると、普通に複雑でむずかしい問題だと思いました。こちら、1度目の提出でACできましたが、書いててイライラするような複雑さです。わかりにくいのでコメントも結構書いています。コンテスト時間内に解き切れる気がしません。適切なデータ構造や変数名を使うことで、解答にかかる時間を短くするスキルが足りないのだと感じます。 2022-12-25

import sys
H, W = map(int, input().split())
A = [[] for _ in range(2)] # 0 original 1 flip
F = {0:(0,0), 1:(0,1), 2:(1,0), 3:(1,1)}
F_ = {(0,0):0, (0,1):1, (1,0):2, (1,1):3}
for _ in range(H):
    A[0].append(list(map(int, input().split())))
    A[1].append([1-a for a in A[0][-1]])
def check_isolate(x, y, flip):
    f0, f1, f2 = flip
    this = A[f1][x][y]
    if 0 < x and A[f0][x-1][y] == this:
        return False
    if 0 < y and A[f1][x][y-1] == this:
        return False
    if x <= H-2 and A[f2][x+1][y] == this:
        return False
    if y <= W-2 and A[f1][x][y+1] == this:
        return False
    return True
dp = [[-1]*H for _ in range(4)]
# check 0
# 0 -> 1
for j in range(4): # flip 1 or not
    flip = (0, *F[j])
    for k in range(W):
        if check_isolate(0, k, flip):
            break
    else: # ok
        dp[j][1] = flip[1] + flip[2]
# check 1 - H-2
for i in range(1, H-1): # i -> i+1
    # try i+1 to make i not isolated
    for j in range(4): # status of i-1 and i
        if dp[j][i] == -1:
            continue
        for f in range(2): # flip i+1
            flip = (*F[j], f)
            for k in range(W):
                if check_isolate(i, k, flip):
                    break # ng
            else: # ok
                count = dp[F_[(flip[0], flip[1])]][i]+1 if f \
                            else dp[F_[(flip[0], flip[1])]][i]
                if dp[F_[(flip[1], flip[2])]][i+1] == -1:
                    dp[F_[(flip[1], flip[2])]][i+1] = count
                else:
                    if count < dp[F_[(flip[1], flip[2])]][i+1]:
                        dp[F_[(flip[1], flip[2])]][i+1] = count
# check H-1
res = 2000
for j in range(4):
    if dp[j][H-1] == -1:
        continue
    for k in range(W):
        flip = (*F[j], 0)
        if check_isolate(H-1, k, flip):
            break
    else: # ok
        if dp[j][H-1] < res:
            res = dp[j][H-1]
if res == 2000:
    print(-1)
else:
    print(res)

さすがに上の解答はACしてもキビシイと思うので、わかりやすく書き直してみます。dpをkeyが(0,0),(0,1),(1,0),(1,1)のdictに変えてみます。上では、0,1,2,3と(0,0),(0,1),(1,0),(1,1)を相互変換するためだけにdpを用意し、ループは0-3でやってタプルに変換したり、逆にタプルを0-3に戻したりしていました。これ、[]のなかで変換用dictにアクセスしたりして手間がかかってミスの温床になりそうでした。はじめからタプルをkeyにします。4つだけですし、この方が明らかにわかりやすいですよね。また、0からH-1の行を表す添字はi、0からW-1の列を表す添字はjで統一します。こういうの流れて変えちゃうのもミスの温床になりそうです。i+1はniという変数に、i+1を反転させるかどうか？は、nfという変数名にしました。niはi+1でアクセスしたり、片方だけnextって付けたりしちゃうこともある気がしますが、こうやって統一感出します。i-1とiのflipのタプル、i-1,i,i+1のflipのタプル、i,i+1のflipのタプルなど相互に作ったりするので、要素数を2のタプルに3つ目の要素を追加するときは、(*f, 1)のように、要素数3のタプルから2つのタプルを作るときは、f[1:]とか、f[:2]のように書くべきですね。 2022-12-25

見直しているときに思ったんですが、たとえば、直近3行のフリップ状態が0,1,0のときに、真ん中の行に孤立要素がない場合、1,0,1でも孤立要素はないですね。なので、計算量半分にはできそうです。まあ半分どころではなく速い提出もちらほらあるようで、そちらはどうなってるのかわかりません。 2023-01-14

import sys
H, W = map(int, input().split())
A = [[] for _ in range(2)] # 0 original 1 flip
for _ in range(H):
    A[0].append(list(map(int, input().split())))
    A[1].append([1-a for a in A[0][-1]])
def check_isolate(x, y, flip):
    f0, f1, f2 = flip
    this = A[f1][x][y]
    if 0 < x and A[f0][x-1][y] == this:
        return False
    if 0 < y and A[f1][x][y-1] == this:
        return False
    if x <= H-2 and A[f2][x+1][y] == this:
        return False
    if y <= W-2 and A[f1][x][y+1] == this:
        return False
    return True
dp = {(0,0):[-1]*H, (0,1):[-1]*H, (1,0):[-1]*H, (1,1):[-1]*H}
# check 0 line isolated
for f in dp: # line 0 and 1 flip status
    for j in range(W):
        if check_isolate(0, j, (0, *f)): # 0 is dummy
            break
    else: # ok
        dp[f][1] = f[0] + f[1]
# check 1 - H-2
for i in range(1, H-1):
    # try ni to make i not isolated
    ni = i + 1
    for f in dp: # status of i-1 and i
        if dp[f][i] == -1:
            continue
        for nf in range(2): # flip ni or not
            flip = (*f, nf)
            for j in range(W):
                if check_isolate(i, j, flip):
                    break # ng
            else: # ok
                count = dp[f][i]+1 if nf else dp[f][i]
                if dp[flip[1:]][ni] == -1:
                    dp[flip[1:]][ni] = count
                else:
                    if count < dp[flip[1:]][ni]:
                        dp[flip[1:]][ni] = count
# check H-1
res = INF = 2000
for f in dp:
    if dp[f][H-1] == -1:
        continue
    for j in range(W):
        if check_isolate(H-1, j, (*f, 0)):
            break
    else: # ok
        if dp[f][H-1] < res:
            res = dp[f][H-1]
if res == INF:
    print(-1)
else:
    print(res)

F - Permutation Distance

解説を見ると場合分けしてセグ木を使うと書いてあったり、マンハッタン距離の最小全域木を求めると言ってる人もいましたが、なかなかむずかしいです。あとで、勉強のためにそちらで解く必要があると思いますが、愚直に近い方から調べて枝刈りしてるだけでACしてる人も多く、まずそれでACしました。シンプルに考えて、この回答に気づけるべき、なのは間違いないですね。 2022-12-25

import sys
input = sys.stdin.readline
N = int(input())
P = [0] + list(map(int, input().split()))
ans = []
for i in range(1, N+1):
    di = 1
    res = N # next farthest
    while True:
        if 0 < i - di:
            res = min(res, di + abs(P[i-di] - P[i]))
        if i + di <= N:
            res = min(res, di + abs(P[i+di] - P[i]))
        di += 1
        if res <= di + 1:
            break
    ans.append(res)
print(*ans)

セグメントツリーで解くのが正攻法のはずなので、セグメントツリーの勉強も兼ねてやってみたのですが、ACx35、TLEx20から全く改善できません。他のPythonとセグメントツリーで解いてる人と、違いがあるように見えないので、ムカつきますがあきらめました。結局ぼくは今まで、セグメントツリーでまともにACした問題がありません。これで1回ACしておくはずだったのですが、腹立つなぁ。 2023-01-09

import sys
input = sys.stdin.readline
INF = 1000000
class SEGT():
    DEFAULT = -INF # need update
    # 省略
    def query(self, a, b, k, l, r):
        if r <= a or b <= l:
            return self.DEFAULT
        if a <= l and r <= b:
            return self.maxima[k]
        else:
            vl = self.query(a, b, k*2+1, l, int((l+r)/2))
            vr = self.query(a, b, k*2+2, int((l+r)/2), r)
            return max(vl, vr)

N = int(input())
P = [0] + list(map(int, input().split()))
D = [INF]*(N+1)
segt = SEGT(N+1)
for i in range(1, N+1):
    D[i] = min(D[i], P[i] + i - segt.query(0, P[i], 0, 0, segt.n))
    segt.update(P[i], P[i] + i)
segt = SEGT(N+1)
for i in range(N, 0, -1):
    D[i] = min(D[i], P[i] - i - segt.query(0, P[i], 0, 0, segt.n))
    segt.update(P[i], P[i] - i)
segt = SEGT(N+1)
for i in range(1, N+1):
    D[i] = min(D[i], -segt.query(P[i]+1, N+1, 0, 0, segt.n) - P[i] + i)
    segt.update(P[i], i - P[i]) # register minus
segt = SEGT(N+1)
for i in range(N, 0, -1):
    D[i] = min(D[i], -segt.query(P[i]+1, N+1, 0, 0, segt.n) - P[i] - i)
    segt.update(P[i], - P[i] - i)
print(*D[1:])

あきらめた。などと言ってあきらめたことはないですね。どうしても気になり続けてしまっていて、コーヒーでも飲んでるときに、ふと改善できる箇所に気づきます。今回は、queryが再帰関数になってるところが遅そうと気づけました。再帰関数をstackに書き直したらACできました。stackに書き直すのも、ササッとこなれたものです。祝、セグ木初AC。最初に書いたのが蟻本のC++をPythonに翻訳して書いたもので、再帰関数やまだ慣れてなかったころの表現がそのままになってました。徐々にわかってくることがあるし、解けない問題に遭遇することで、ライブラリがまともなものに更新されていきます。うまくいかないとき、ちゃんと解決しておくことで、次解ける問題が増えていくので、あきらめるのはNGです。ABC266 Ex - Snuke Panic (2D)は、2次元フェニック木で解けたけど、2次元セグメント木ではTLEでした。これも今ならACできるのか？ちょっと気になります。→ダメ、その後さらに高速化してもダメ。 2023-01-09

import sys
input = sys.stdin.readline
INF = 1000000
class SEGT():
    DEFAULT = -INF # need update
    # 省略

    def query(self, a, b):
        ret = self.DEFAULT
        stack =[(0, 0, self.n)]
        while stack:
            k, l, r = stack.pop()
            if r <= a or b <= l:
                pass
            elif a <= l and r <= b:
                ret = max(ret, self.maxima[k])
            else:
                stack.extend([(k*2+1, l, (l+r)//2), (k*2+2, (l+r)//2, r)])
        return ret

N = int(input())
P = [0] + list(map(int, input().split()))
D = [INF]*(N+1)
segt = SEGT(N+1)
for i in range(1, N+1):
    D[i] = min(D[i], P[i] + i - segt.query(0, P[i]))
    segt.set(P[i], P[i] + i)
segt = SEGT(N+1)
for i in range(N, 0, -1):
    D[i] = min(D[i], P[i] - i - segt.query(0, P[i]))
    segt.set(P[i], P[i] - i)
segt = SEGT(N+1)
for i in range(1, N+1):
    D[i] = min(D[i], -segt.query(P[i]+1, N+1) - P[i] + i)
    segt.set(P[i], i - P[i]) # register minus
segt = SEGT(N+1)
for i in range(N, 0, -1):
    D[i] = min(D[i], -segt.query(P[i]+1, N+1) - P[i] - i)
    segt.set(P[i], - P[i] - i) # register minus
print(*D[1:])

G - Partial Xor Enumeration

参加し始めたABC266から、問題Gを埋めていましたが、2022年ラストABCの問題G、かなり苦労してようやくACしました。知らないことが多すぎて勉強が大変でした。線形代数の教科書も出してきて、読んでました。現在Python3での提出中、なぜか最速の287msで、ちょっとうれしいです。遅いとなんで遅いのか？とまた気になってしまいますからね。この問題を解くために「XOR基底」というものを勉強しました。1度それを勉強してしまうと、この問題はXOR基底を求めて解く問題としか思えなくなります。「XOR基底」とは、数列A内の部分列のXORが作る空間の基底のことですから。基底とは何かというと、数列AのXOR空間をすべてカバーできる線形独立な集合です。それを求めるにはnoshi基底という方法を使いす。Pythonならこうなります。シンプル！

base = []
for a in alist:
    for e in base:
        if a^e < a:
            a ^= e
    if a:
        base.append(a)

XOR基底自体初めて勉強したので、最初見たときは、ちんぷんかんぷん過ぎたのですが、今現在ぼくがnoshi基底をどのように理解しているか？書いてみます。この方法で得られたbaseは、最上位bitがすべて異なります。if a^e < a:のところを見てください。このif文の条件を満たすのは、aの中の、すでに登録済みの基底の最上位bitの桁が1から0になる時だけです。つまり、aの中の、すでに登録済みの基底の最上位bitの桁を、全部0にする処理なのです。その処理が終わって0でなければ、aを新しい基底として登録します。この時点でaの最上位bitは、登録済みのすべての基底の最上位bitと異なります。同じであれば、if文の処理で、0に変えられてしまうからです。よって、この処理が終わった時点で、baseに登録された基底は最上位bitがすべて異なることがわかります。基底を成すために、最上位bitがすべて異なる必要があるのかどうかは、わかりません。しかし、最上位bitが異なる値の集合が線形独立であることは明らかです。（明らかではないかもしれないので、下に追記があります。）つまり確実に線形独立な集合が作られることはわかります。ではここで作られた線形独立なbaseは、数列AのXOR空間をすべてカバーしているのかどうか？最初不思議に感じましたが、実は数列Aのすべての要素をbaseに登録された基底で作ることができれば、カバーできていると言えます。何が不思議と感じたかって、たとえば、ai^aj^akが基底の組み合わせだけで表現されないといけないわけですが、ai=e1、aj=e1^e2、ak=e1^e3だった場合、「あれ？e1が3つも出てきたぞ！使えるのは1つまでなのに！」って疑問が湧きませんか？でもそんな心配は不要です。XORの性質から、e1^e1^e1=e^1なのです。2つ使うと必ず0個に戻ってくれるので、何個使っても1つ以上使えないのです。これはXORの不思議な性質で、楽しいですね。よって、すべてのaを基底から作ることができれば、基底の作るXOR空間は数列AのXOR空間と一致します。さて、すべてのaはbase内の基底のXORで作れるのか？これはnoshi基底の処理中、a^=eという処理しかしていないことから、当然eのXORでaを作れるように処理を進めているのです。（eはaそのものか、aといくつかのeとXORを取って作られています。処理中0になって基底に登録されなかったものは当然ながら、eの組み合わせでできています。）よって、上記で得られたnoshi基底は、確かに数列AのXOR空間の基底を成しています。どうやっても同じ変数を2個以上XORできないという、XORの気持ちいい性質、すばらしいですよね。eはaを元にしてXORだけを使って作っているのだから、aを組み合わせてXORすればそれぞれのeを作れるし、（あ、これはeの中にaから作れないような余計なものがないことの証明として大事ですね。）aで作ったeを組み合わせてXORすればそれぞれのaを作れるわけです。もう一度証明を一言でまとめると、「noshi基底は最上位bitが異なることから線形独立であり、数列Aのすべての要素をnoshi基底のXORで作れることから、AのXOR空間とnoshi基底のXOR空間が一致するため、XOR基底となっていることがわかる。」この問題では、AのXOR空間の要素を小さい順に列挙する必要がありますので、すでに登録した基底要素の中に新しい基底要素の最上位bitの桁が1のものが含まれていた場合、消す処理を、追加でほどこしています。このようにすることで、確実に昇順に列挙することができています！いやー大変だった。 2023-01-04

noshi基底の証明で「最上位bitが異なるので線形独立」と書いた部分が本当か？と、ちょっともやもやしたので追記します。この問題においては、基底を作る処理中で新しい基底要素を追加するときに、最上位bitと同じ桁が1の登録済み基底要素があれば、0にし、最上位bitは絶対に1つしかない状態にしています。この方が線形独立であることは明らかでわかりやすいように思います。元のnoshi基底の生成では110を登録したあとで10が登録されうるように、ある基底要素の最上位bitと同じbitが立っている他の基底要素が存在しうるので、本当に大丈夫か？とちょっと不安になるかもしれません。しかしやはり最上位bitが異なれば、その組み合わせのXORで生成される値はすべて異なることを示せます。e1,e2,e3,..と基底要素を昇順に並べたとします。小さい順に使うか使わないか？を決めて値を生成すると、0→e1→e2,(e1,e2)→e3,(e1,e3),(e2,e3),(e1,e2,e3)→…というように倍々で新しい値を生成できますが、新しい基底要素を追加したときに初めてその最上位bitが立つはずなので、同じ値が作られることは、やはりありえません。「最上位bitが異なるので線形独立」というのは正しいです。安心です。 2023-01-04

import sys
input = sys.stdin.readline
N, L, R = map(int, input().split())
base = []
for a in map(int, input().split()):
    for e in base:
        if a^e < a:
            a ^= e
    if a:
        for i, e in enumerate(base):
            if a^e < e:
                base[i] ^= a
        base.append(a)
base.sort()
def calc(i):
    res = 0
    keta = 0
    while i:
        if i&1:
            res ^= base[keta]
        i //= 2
        keta += 1
    return res
ans = []
for i in range(L-1, R):
    ans.append(calc(i))
print(*ans)

AtCoder Beginner Contest 284

新年最初のABC。4回ぶり4度目の5完でした。1ヶ月、5完から遠ざかってましたがようやくです。今回は6問目の問題Fに50分近く残っていて、初めて解けるかもしれないと緊張しましたが、解けませんでした。SA-ISで、いけるかなー？という方針を思いつき、やってましたが、ロジックが煩雑になってしまいました。

D - Happy New Year 2023

素因数分解の典型的なやり方だとTLEでした。ひっかけで初笑いです。Nはq*p^2で表せるという条件があるので、1つ目の素因数が見つかった時点で、ループを打ち切って残りを計算すればよいです。3つの素数の積なので、最も小さいものは、9*10^18の3乗根、すなわち約200万より小さいことがわかるので、短時間で見つかりますね。pかqが比較的小さくて、もう一方を見つけるためにループを回し続けると、計算量が膨大になってしまいますね。qが先に見つかったときに、pを計算するところで、平方根を小数で計算したものをintに変換していますが、これは安全なのでしょうか？不安なら+1、-1の値で正当性検証した方が良いかもしれません。 2023-01-07

T = int(input())
for _ in range(T):
    N = int(input())
    a = 2
    while a*a <= N:
        if N % a == 0:
            N //= a
            if N % a == 0:
                print(a, N//a)
            else:
                print(int(N**0.5), a)
            break
        a += 1

E - Count Simple Paths

DFSで、帰りがけにusedをFalseにすることで正しくカウントできました。コンテスト中に解けてスッキリです。 2023-01-07

N, M = map(int, input().split())
G = [[] for _ in range(N)]
for _ in range(M):
    u, v = map(int, input().split())
    G[u-1].append(v-1)
    G[v-1].append(u-1)
stack = [-1, 0]
used = [False]*N
ans = 0
while stack:
    cur = stack.pop()
    if cur >= 0:
        used[cur] = True
        ans += 1
        if ans == 1000000:
            break
        for next in G[cur]:
            if not used[next]:
                stack.extend([~next, next])
    else:
        used[~cur] = False
print(ans)

F - ABCBAC

コンテスト時間中にSA-ISで解こうとして時間切れになりました。解説によるとZ algorithmというものが使えるようです。名前だけ聞いたことがありましたが、この機会に初めて勉強できました。文字列のすべての接尾辞について、その文字列の先頭からと何文字一致しているか？をO(N)で計算できます。考え方もコードもシンプルで、すごくいいです。これを知ってしまうと、この問題はZ algorithmで解くとしか思えなくなってしまいました。Z algorithmを知ることができて良かったです。 2023-01-07

import sys

def z_algorithm(s):
    n = len(s)
    z = [0]*(n)
    z[0] = n
    i = 1
    j = 0
    while i < n:
        while i+j < n and s[j] == s[i+j]:
            j += 1
        z[i] = j
        if j == 0:
            i += 1
            continue
        k = 1
        while i+k < n and k+z[k] < j:
            z[i+k] = z[k]
            k += 1
        i += k
        j -= k
    return z

N = int(input())
N2 = 2*N
T = input()
mae = T[:N]
ato_rev = T[N:][::-1]
if mae == ato_rev:
    print(mae)
    print(N)
    sys.exit()
X = mae + ato_rev
Y = ato_rev + mae
ZX = z_algorithm(X)
ZY = z_algorithm(Y)
for i in range(1, N):
    if ZX[N2-i] == i and ZY[N+i] == N-i:
        print(T[:i]+T[i:N][::-1])
        print(i)
        break
else:
    print(-1)

ローリングハッシュを使ったことがないので、ローリングハッシュでもやってみました。ABCに参加し始めて、比較的早い段階でこの言葉に出会っていましたが、その時は、他の方法でも解けたので後回しにして、ずっと気になっていました。まず、蟻本の該当ページを読みましたが、これだと文字列中の固定幅のハッシュ値しか計算していませんね。この問題では、幅を変動させながら調べる必要があるので、接頭辞全体のハッシュ値を求めておき、指定した範囲のハッシュ値は左右の値から計算する必要があります。やってみました！最初蟻本に書いてあった通りmodを計算するH=2^64として実行したところ、WAx5、TLEx19となってしまいました。どうも2^64を使うとハッシュ値が衝突するような意地悪問題を作れるらしいです。さらに遅い。そこで、ネットで見つけたH=2^61-1を使用したところ、なんとACです。こういうのやってみないとわからないし、ローリングハッシュで初めてトライしてみて良かったです！ 2023-01-08

import sys
B = 100000007
# H = 2**64
H = 2**61 - 1
N = int(input())
N2 = 2*N
T = input()
mae = T[:N]
ato_rev = T[N2-1:N-1:-1]
if mae == ato_rev:
    print(mae)
    print(N)
    sys.exit()
X = mae + ato_rev
hash = [0]*(N2+1) # 0 is empty 1-N2 is char
Bexp = [0]*(N2+1)
Bexp[0] = 1
for i, c in enumerate(X): # X[i] -> hash[i+1]
    hash[i+1] = (hash[i] * B + ord(c)) % H
    Bexp[i+1] = Bexp[i] * B % H
def hash_range(l, r):
    return (hash[r] - hash[l] * Bexp[r-l]) % H
for i in range(1, N):
    if hash_range(0,i) == hash_range(N2-i,N2) \
    and hash_range(i,N) == hash_range(N,N2-i):
        print(T[:i]+T[N-1:i-1:-1])
        print(i)
        break
else:
    print(-1)

G - Only Once

なもりグラフができて、巡回するまでの個数、ということまではわかったんですが、対称性があるのでB1だけ考えて、N倍すればいいってことに気づけませんでした。気づきたいですし、この問題は解けたいですね。問題Gの壁はなかなか破れません。 2023-01-08

N, M = map(int, input().split())
# for x 1-N
# where x is reachable num count from 1
perm = [0]*(N+1)
perm[1] = 0
if N > 1:
    perm[2] = (N-1) % M
    for x in range(3, N+1):
        perm[x] = perm[x-1] * (N-x+1) % M
expo = [0]*(N+1)
expo[N] = 1
for x in range(N-1, 0, -1):
    expo[x] = expo[x+1] * N % M
ans = 0
for x in range(1, N+1):
    ans += perm[x] * (x*(x-1)//2) * expo[x]
    ans %= M
print(ans*N%M)

AtCoder Regular Contest 153

これまで土曜日にABCに参加していましたが、今週はARCが土曜日でABCが日曜日ということで、この機会にとARCに初参加しました。「なぜABCとARCの曜日が逆？」と思ったのですが、ぼくが参加し始めてから、たまたましばらくARCの日曜開催が続いていただけで、曜日が決まってるわけではないみたいです。で、結果はA1完。洗礼を受けました。ARCの感想ですが、まず、ABCより難しいです。そしてコンテスト終了後、問題B、Cしかやってませんが、アルゴリズム適用したらいけます的な問題ではなく、考えてひらめくことの方に重点があるように感じました。

B - Grid Rotations

問題は2次元の180度回転ですが、1次元の区間反転の問題として解けば良い、ということまではわかり、間に合わないのが明らかであるにも関わらず、数列をスライスで反転してました。当然のごとく、ACx19、TLEx13から前に進めず、諦めました。解説に書いてあることがぶっ飛んでいて、両端もつながっていると考えれば、実はこの操作を何度やっても、数列が崩れないとのことでした。Q回の操作は、全体のスライドと反転を1回やる操作と考えられるのです。なので、0の位置だけ追いかければ、最後の状態を簡単に復元できます。うーん、どうやったら気づけるのかなぁ？そういえばこの問題を解いているときに「え？」って思ったことがありました。これなんですけど、リストのスライスで、l2=[4,3,2,1]が欲しいとき、最後を-1で表現できないんですね。空のリストになってしまいちょっと驚きました。rangeだと0までの値を返してくれるのですが。 2023-01-15

>>> l = [1,2,3,4]
>>> l2 = l[3:-1:-1]
>>> l2
[]
>>> [i for i in range(3,-1,-1)]
[3, 2, 1, 0]

import sys
input = sys.stdin.readline
H, W = map(int, input().split())
alist = []
for _ in range(H):
    alist.append(input())
Q = int(input())
h0 = 0
w0 = 0
for _ in range(Q):
    a, b = map(int, (input().split()))
    h0 = (0 if h0 < a else H) + a - 1 - h0
    w0 = (0 if w0 < b else W) + b - 1 - w0
if Q & 1 == 0:
    hindex = (list(range(H))*2)[H-h0:2*H-h0]
    windex = (list(range(W))*2)[W-w0:2*W-w0]
else:
    hindex = (list(range(H-1,-1,-1))*2)[H-h0-1:2*H-h0-1]
    windex = (list(range(W-1,-1,-1))*2)[W-w0-1:2*W-w0-1]
for i in hindex:
    line = []
    for j in windex:
        line.append(alist[i][j])
    print(''.join(line))

C - ± Increasing Sequence

解説を見ても、懇切丁寧に説明されているわけではなく理解に苦しみました。狭義単調増加の数列を、隣同士の差の数列に置き換えることで自然数列にするというのはよくあると思います。が、やっても、ぼくには何も見えてこなかったです。解説は、「実際にこのように考えれば目的の数列を生成することができます。」ということをやっています。自然数列のベースとしてまず全部1にしてみる、というのも良い手なのかもしれません。全部1を入れておいて、合計0に足りない分や、多すぎた分を1箇所で調整するということをしていました。場合分けが妙で、数列Aの後ろからの累積和を作っており、合計が0かどうかでも分岐しています。0でない場合は、全部1以外の値を設定して、最初の値だけ別の値を入れて調整していました。いや逆だな、blist[0]が0でない場合をやって、0の時どうするんだ？という思考順序ですね。今の自分には、コンテスト中に思いつける気がしないというのが正直な感想です。 2023-01-15

import sys
input = sys.stdin.readline
N = int(input())
alist = list(map(int, input().split()))
blist = [0]*N
blist[N-1] = alist[N-1]
for i in range(N-2, -1, -1):
    blist[i] = blist[i+1] + alist[i]
bsum2 = sum(blist[1:])
ans = [0]*N
if blist[0] != 0:
    ans[0] = (-1 if blist[0] > 0 else 1) * bsum2
    absb0 = abs(blist[0])
    for i in range(1, N):
        ans[i] = ans[i-1] + absb0
else: # blist[0] == 0
    id1 = -1
    id_1 = -1
    for i in range(N):
        if blist[i] == 1:
            id1 = i
        elif blist[i] == -1:
            id_1 = i
    if id1 == -1 or id_1 == -1:
        print('No')
        sys.exit()
    ans[0] = 1
    for i in range(1, N):
        ans[i] = ans[i-1] + 1
        if i == id_1 and bsum2 >= 0:
            ans[i] += bsum2
        elif i == id1 and bsum2 < 0:
            ans[i] -= bsum2
print('Yes')
print(*ans)

D - Sum of Sum of Digits

★ 理解するのに、今までで一番苦労した問題となりました。大変でしたが、桁でDPする問題を「桁DP」と呼ぶらしく、初めての桁DPとして、どうしてもACしたかったのでがんばりました。xlistに登録されている値は、10^i-a%(10^i)、すなわち10^iの桁に繰り上がるためにに必要な値ということになります。それに0（0個繰り上がる値）も要素として追加しています。解説にあるように、N個のうち、何個の値が繰り上がるのか？をDPのキーとしますが、x%(10^i)の値を決めたときに、xlistのどこにあるのかを確認すれば、何個繰り上がるのかわかることになります。x%(10^i)=0であれば0個、最大値ならN個繰り上がることがわかります。DPの遷移中、m_carryは10^iに繰り上がる個数、n_carryは10^(i+1)に繰り上がる個数で、それぞれ別の求め方をしています。i=0のところは面倒ですが、ちょっと特別扱いしています。一度ACしてしまうと、ACするまでの苦労が何もなかったかのように忘れてしまうし、自分で読んでもわからなくなりそうですが、記録のためになんとか思い出せることを書きたいと思います。DPのところで、x%(10^i)からx%(10^(i+1))を作るところ、i桁目をkとし、k*10^i+x%(10^i)としています。これでいいのか？って結構悩みました。というのも、x%(10^i)ってm個繰り上がるための最小値ですよね。なので、xlist[i]の中で、「次に小さい値未満」なら、繰り上がる個数は同じmです。その値に対してk*10^i+x%(10^i)からn_carryを求めると、n_carryが増える可能性があるのではないか？という疑問です。これ、結局のところありえないということがわかったので、bisect_right1回でn_carryを求めています。なぜありえないのかというと、よく考えたらxlist[i+1]の要素って、xlist[i]の要素+k*10^iしかありえないんです。ということは、m_carryが同じx%(10^i)の値に対して、n_carryの値が異なるということはありえないんです。その部分はxlist[i+1]でも、xlist[i]と同じように必ず空白になっているはずなんです。もしかすると、桁DPで必要な重要な感覚かもしれまえん。下の桁で抜けてる部分はその上の桁がどんな値でも抜けたままだよ、と。というわけで、全部書こうとしてもあれなので、終わりとします。ものすごく苦労したことで、今後「桁DP」に出会ったときに、少しでも自力でACできる可能性が高まりますように。そうでなければ割に合わないしんどさでした。それにしても、解けてない問題を抱えて過ごすのってストレスですね。 2023-02-04

import bisect
N = int(input())
alist = list(map(int, input().split()))
digimax = len(str(max(alist)))

pow10 = [1]*(digimax+1)
for i in range(1, digimax+1):
    pow10[i] = pow10[i-1] * 10

xlist = [[0]*(N+1)] + [sorted([pow10[i] - a % pow10[i] for a in alist] + [0]) for i in range(1, digimax+1)]

dp = [{} for _ in range(digimax+1)]
for i in range(N+1):
    dp[digimax][i] = i
for i in range(0, digimax)[::-1]:
    asum = 0
    for j in range(N):
        asum += alist[j] // pow10[i]
        alist[j] %= pow10[i]
    prev = -1
    for j in range(N+1)[::-1]:
        if xlist[i][j] != prev:
            x = xlist[i][j]
            prev = x
            m_carry = j if i > 0 else 0
            curmin = 10**9
            # xの上の桁kでループする
            for k in range(10):
                # n_carry = 1つ上の桁で何個繰り上がったか？kが決まると決まる
                n_carry = bisect.bisect_right(xlist[i+1], k*pow10[i]+x) - 1
                # asum = 1つ上の桁の合計
                # それに桁上りm_carryを加えて、xはkがN個全体に加えられて、その上にさらに上がった分10*n_carryは引く
                curmin = min(curmin, dp[i+1][n_carry] + asum + m_carry - 10*n_carry + k*N)
            dp[i][m_carry] = curmin

print(dp[0][0])

AtCoder Beginner Contest 285

4完。参加し始めて、初めての日曜開催のABCです。4ヶ月もやってるので、てっきり例外的な日曜開催なのかと思いましたが、たまたまらしいです。開始時刻に間違ってABC286のページを開いており「あれ？はじまらねーぞ？」と、あわててABC285の参加登録をするというハプニングがあり、しばらく動揺してしまいました。そのせいでパフォーマンス落ちた？わかりませんが。問題E、DPのコードを書いて、終わりかけの時間に提出しましたが、NGでした。よくないDPを設計して実装してしまいましたが、解説見ると、解けた問題だったかもなぁと、くやしい。というのも、5問解けていたらどんなに遅くても、過去最高順位とパフォーマンスが出ていたっぽいんですよね。甘くないです。

B - Longest Uncommon Prefix

ABCの問題文は、読んでてたまに発狂しそうになりますが、この問題が今までで最悪だったかもしれません。思考停止しました。開始時刻のトラブルのせいなのか？わかりませんが、同じような感想も見かけました。今見てもちょっと混乱してしまうんですが、breakしたら、1つ前まで≠なのでl=k-1が答え、breakしなかったら最後まで≠なので、l=kが答えってことでいいですね。気づいてませんでしたが、タイトルをよく見たらLongest Uncommon Prefixですか。LCPから着想を得た問題と思うと、意味を理解しやすい可能性があり。タイトルも有益な情報源。 2023-01-15

N = int(input())
S = ' ' + input()
for i in range(1, N):
    for k in range(1, N-i+1):
        if S[k] == S[i+k]:
            break
    else:
        print(k)
        continue
    print(k-1)

D - Change Usernames

変更先のユーザ名が、現在存在する場合は、変更できないので、そっちを先に変更する必要があります。その変更先のユーザ名が、存在する場合、そっちを先に変更する必要があります。これが元のユーザに戻ってきてしまうと、どれも変更できないので、グラフを作って順回路の存在チェックをする問題でした。そこまでくると基本的な問題に帰着したと思いますが、何度かデバッグして修正が必要だったので、まだまだです。 2023-01-15

import sys
N = int(input())
g = [[] for _ in range(2*N)]
sdict = {} # name -> id
tlist = []
for i in range(N):
    s, t = input().split()
    sdict[s] = i
    g[i].append(i + N)
    tlist.append(t)
for i, t in enumerate(tlist):
    if t in sdict:
        g[i + N].append(sdict[t])
used = [False for _ in range(2*N)]
for i in range(2*N):
    if used[i]:
        continue
    stack = [i]
    used[i] = True
    while stack:
        cur = stack.pop()
        for next in g[cur]:
            if not used[next]:
                stack.append(next)
                used[next] = True
            elif next == i:
                print('No')
                sys.exit()
print('Yes')

E - Work or Rest

コンテスト時間中、DPでやろうと思い、連続する平日の生産性をまず、事前に計算して用意しました。ここまでは正しい流れです。DPをどのように設計するか？ですが、横軸iを設定した休日の数、としてしまいました。その状態での生産性をDPの値とし、その翌日からN日までの間の曜日に休日を設定する時に、最後の連続する平日の生産性を引いて、分割した平日の生産性を2つ足してDPが遷移していくというような設計です。なんか気持ち悪いと思ってましたが、時間内に提出した回答は、TLEが大量発生しました。解説の方法はスマートですね。i曜日まで、確定したということを横軸にしていました。i曜日までしか見たくないですよねー。という感じです。自然にこのDPを思いついて、時間内に解きたかったです(T_T) 2023-01-15

import sys
N = int(input())
if N == 1:
    print(0)
    sys.exit()
alist = list(map(int, input().split()))
asum = [0]*N
asum[0] = alist[0] # production sum from 0-i
for i in range(1, N):
    asum[i] = asum[i-1] + alist[i]
between = [0]*N
between[1] = asum[0] # 1day
for i in range(2, N):
    if i % 2 == 0:
        between[i] = 2*asum[i//2-1]
    else: # odd
        x = i // 2
        between[i] = asum[x] + asum[x-1]
dp = [0]*(N+1)
for i in range(1, N): # i -> i+1
    dp_new = [0]*(N+1)
    for j in range(0, i):
        dp_new[0] = max(dp_new[0], dp[j] + between[j])
        dp_new[j+1] = dp[j]
    dp = dp_new
ans = 0
for i in range(N):
    ans = max(ans, dp[i] +between[i])
print(ans)

F - Substring of Sorted String

解説を見たんですが、この問題を通じてセグメントツリーの速度改善ができたので、良かったです。セグメントツリーでやると書いてあり、自分のセグメントツリーを使ってやったところ、TLEが解消できなかったんです。そして他の方のセグメントツリーを見て、queryの効率的な実装を知ることができました。これまでのABCでの経験から、セグメントツリーが遅いと思っていて苦手意識があったんです。遡れば、セグメントツリーとの出会いは、初めて参加したABC266 Exでした。そのとき、セグメントツリーを知らないのに、いきなり最初から2次元セグメントツリーを使って、TLEでした。フェニック木ではACできたのに！セグメントツリーの印象が悪くなりました。セグメントツリーに次に出会ったのは、もう最近で、ABC283 Fです。このときもTLEしたのですが、なんとしてもセグメントツリーで1問解くんだ！と思い、蟻本を見て実装したqueryが再帰関数であることに気づき、stackに変更することで初めてセグメントツリーでACできました。ライブラリーを改善できたんだと思って臨んだこの問題でまたもやTLEで、気が滅入りましたが、他の方の提出を見ていて、全く無駄のないqueryの実装を組み込むことができました。これきれいですね。蟻本ではrootから下っていきながらqueryを処理していますが、この方法では、下から親に上っていき、無駄が全くありません。でも1度知ってしまうと、極めて自然な実装と思え、蟻本がなんであんな実装になっているのか不思議なくらいです。蟻本を見て実装したコードは再帰呼び出しをしていました。k, l, rという引数があり、kはノードのインデックスで、[k]が[l, r)の範囲を持っているという意味です。呼び出し時には、(k, l, r) = (0, 0, n)などとして呼び出します。

def query(self, a, b, k, l, r):
    if r <= a or b <= l:
        return self.DEFAULT
    if a <= l and r <= b:
        return self.maxima[k]
    else:
        vl = self.query(a, b, k*2+1, l, int((l+r)/2))
        vr = self.query(a, b, k*2+2, int((l+r)/2), r)
        return max(vl, vr)

ABC283 Fで再帰呼び出しが遅いと気づき、自分でstackで書き直しました。引数のk, l, rいらないじゃん、と思いました。ABC283 Fは再帰呼び出しでTLE、stackでACで、改善したと思い喜んでいました。

def query(self, a, b):
    ret = self.DEFAULT
    stack =[(0, 0, self.n)]
    while stack:
        k, l, r = stack.pop()
        if r <= a or b <= l:
            pass
        elif a <= l and r <= b:
            ret = max(ret, self.maxima[k])
        else:
            stack.extend([(k*2+1, l, (l+r)//2), (k*2+2, (l+r)//2, r)])
    return ret

そして今回の改善したコードに至ります。本問題、ABC285 FがTLEからACとなりました。いや～確かにこれでいいですよね。ボトムアップで無駄なし。

def query(self, a, b):
    resL = resR = self.DEFAULT
    a += self.n - 1
    b += self.n - 1
    while a < b:
        if a & 1 == 0:
            resL = max(resL, self.maxima[a])
            a += 1
        if b & 1 == 0:
            b -= 1
            resR = max(resR, self.maxima[b])
        a >>= 1
        b >>= 1
    return max(resL, resR)

2023-01-16

import sys
input = sys.stdin.readline
class SEGT():
    DEFAULT = 0 # need update
    def __init__(self, n):
        '''input n is maxid+1, this is 0 start'''
        self.n = 1
        while self.n < n:
            self.n *= 2
        self.sums = [self.DEFAULT]*(2*self.n)
    def set(self, k, a):
        k += self.n - 1
        diff = a - self.sums[k]
        if diff == 0: # not changed
            return
        self.sums[k] += diff
        while k > 0:
            k = (k-1) // 2
            self.sums[k] += diff
    def query(self, a, b):
        resL = resR = self.DEFAULT
        a += self.n - 1
        b += self.n - 1
        while a < b:
            if a & 1 == 0:
                resL += self.sums[a]
                a += 1
            if b & 1 == 0:
                b -= 1
                resR += self.sums[b]
            a >>= 1
            b >>= 1
        return resL + resR

N = int(input())
ORDA = ord('a')
S = [0] + [ord(c)-ORDA for c in input()]
Q = int(input())
alphabets = [SEGT(N+1) for _ in range(26)]
count = [0]*26
ascend = SEGT(N+1) # [i] = [i-1]<[i]
for i in range(1, N+1):
    c = S[i]
    count[c] += 1
    alphabets[c].set(i, 1)
    ascend.set(i, 1 if S[i-1] <= S[i] else 0)
for _ in range(Q):
    q = input().split()
    if q[0] == '1':
        x = int(q[1])
        c = ord(q[2]) - ORDA
        if c != S[x]:
            prec = S[x]
            S[x] = c
            count[prec] -= 1
            alphabets[prec].set(x, 0)
            count[c] += 1
            alphabets[c].set(x, 1)
            ascend.set(x, 1 if S[x-1] <= S[x] else 0)
            if x < N:
                ascend.set(x+1, 1 if S[x] <= S[x+1] else 0)
    else:
        l = int(q[1])
        r = int(q[2])
        if ascend.query(l+1, r+1) == r - l:
            for c in range(S[l]+1, S[r]):
                if alphabets[c].query(l+1, r+1) != count[c]:
                    print('No')
                    break
            else:
                print('Yes')
        else:
            print('No')

G - Tatami

★ ものすごい苦労しました。ABC274 G以来の2部マッチングですが、とにかく時間制限が厳しかったです。2部グラフの問題かなぁと、問題を読んだ時点でなんとなく想像できるのですが、わかりません。2部グラフかなぁ？と言いつつも、まず1x2のどっちのマスをどっちのグループに入れればいいのかわからないじゃん！というのが素人にとっての壁です。これは隣同士は必ず逆のグループになるので、チェック柄にして2つに分けてしまえばよいのです。素人にとっては、こんな些細なことも、割と重要な事実です。その気持を忘れないように、ここに記載しておかなければなりません。解説を読むと、「最小流量制限つき最大流問題」と書かれています。これが説明を読んでも全く理解できず、なかなか前に進めませんでした。なにか手がかりはないか？と別解の方を見ると、2部グラフの最大マッチング問題に帰着できると書かれています。これは確かに理解できます。わかりやすい。ただし頂点数が2倍になってPythonにとっては、時間制限がかなり厳しくなります。Dinic法をABC274 Gで書いていたので、それを持ってきて実行しましたが、TLEx11をどうしても解消できませんでした。以前書いたDinic法は蟻本に書かれていたものをPythonで書いただけなので、DFSで再帰呼び出しなど使っていました。また再帰呼び出しか？と思い、いつものようにスタックに書き直しても全然速くなりません。調べていると、BFSとDFSを逆方向から行うと良いことがわかりました。これ、かなりすごいと思いました。BFSとDFSを同じ向きでやっていると、DFSの時にTを通り過ぎて、もっと深いところに行ってしまう可能性があります。が、BFSをTからやっていると、なからずTに向かって吸い込まれていくイメージなのです。すごくないでしょうか？理解したとき、ちょっと感動しました。さらに、蟻本では1つの経路が見つかるたびに、DFSを呼び直す実装でしたが、1回のDFSで全部調べきることも可能であることに気づきました。そして作ったのがこの再帰もスタックもないコードです。むちゃくちゃ速くなるんじゃないか？とちょっと興奮して提出しましたが、なんと、TLE解消できず。ショックすぎますね。そこから完全マッチングでの回答をあきらめ、「最小流量制限つき最大流問題」を理解することにしたのです。面食らいますが、最小流量bが決まっているu-vエッジはキャパから最小流量bを引いてしまい、引いたbはSSという別ソースからvへ、uからTTという別のシンクへキャパbのエッジで接続することで、SSからTTへ全部のbの合計が流れるか？調べる問題に書き換えることができます。もとのS、Tはどうするかというと、TからSに向かってキャパ無限のエッジを接続します。最初これがよくわからなかったのですが、元々最大流問題って、Sには無限に入ってくるし、Tからは無限に出ていくことができる前提なのです。そしてSから出る流量とTから出る流量は一致しています。TからSに向かってキャパ無限のエッジを接続しておくことで、この条件は自動的に満たすことになるのです。S、Tは特別なノードであることから、その性質を忘れてしまっているとちょっと驚いてしまいますが。よって、この状態でSSからTTへ最大流問題を解き、SSとTTに接続したすべてのエッジのキャパを使い尽くせるか？調べればよいです。理解して流してもTLEx2。マジで気が滅入りますが、最後はDFSの中のif文を回避するように修正してなんとかACできました。これでも提出の中で遅いですし、みんなどんなコードで最大流問題解いてんだろう？ 2023-01-20

その後進展がありまして、自分の結果が妙に遅いし、AtCoderのサーバーの調子次第なのか、ACした同じコードでもまたTLEするようになってしまいまして、さらに高速化の必要性にせまられていました。で、ヒントはないかと、他の方のコードを見ていたところ、ほぼ100%、BFSをSから、DFSをTからやっていることに気づきました。藁にもすがる思いでそのように書き直したところ、ついに少し余裕を持ってACできました。いや、なんでそれで速くなるのかはいまいちわかってないのですが。最終的に、使い回せるように書き換えてこのようになりました。細かい修正を何度もしており、試行錯誤の集大成みたいな感じです。しかしDFS1回で済ませるのとか、我ながら興奮したしがんばったのに、効果がうすいし、逆にself.nodes[0]をdummyにすることで、if文減らしたのが結構効いたり、なぜかBFSをTからではなく、Sからやるようにしたら効いたり、努力や感動と、結果が比例してなくて悲しいなぁ。ABC285はFでセグ木を、GでDinic法を洗練させる大事な回となりました。あ、あとTからSにキャパ無限のエッジを接続するのと別の方法として、TとSは接続せず、SS→TT、SS→T、S→TTの順に最大流問題を解き、それぞれf1、f2、f3流れたとすると、f1+min(f2, f3)が最小流量を満たすか調べるという方法もあります。SS、TTを優先的に流して最小流量を満たすか確認する必要があるため、この順序となります。最大流も求める場合は最後にS→Tでも最大流問題を解きますが、本問題では、最小流量を満たせるかどうか？がわかれば良いので、S→Tを流す必要はありません。また、最後に、別解の完全マッチング問題に帰着する方も修正後のDinic法でやってみましたが、TLEが減ったもののTLEx4でフィニッシュとなりました。C++でしか間に合わない別解が書かれてるのはつらいです。マッチングのみなら専用のアルゴリズムを使っている人もいるので、そっちなら間に合うのかもしれません。ABC274 GでNetworkXで使ったやつですね。 2023-01-21

H, W = map(int, input().split())
grids = [input() for _ in range(H)]
HW = H*W
S = HW
T = HW + 1
SS = HW + 2
TT = HW + 3
mf = MaxFlow(HW + 4)
count2A = 0
count2B = 0
for i in range(H):
    for j in range(W):
        if grids[i][j] == '1':
            continue
        v = i * W + j
        if (i ^ j) & 1 == 0: # v is in A
            if grids[i][j] == '2':
                count2A += 1
                mf.add_edge(SS, v, 1)
            else: # ?
                mf.add_edge(S, v, 1)
            if i > 0 and grids[i-1][j] != '1':
                mf.add_edge(v, v - W, 1)
            if i < H-1 and grids[i+1][j] != '1':
                mf.add_edge(v, v + W, 1)
            if j > 0 and grids[i][j-1] != '1':
                mf.add_edge(v, v - 1, 1)
            if j < W-1 and grids[i][j+1] != '1':
                mf.add_edge(v, v + 1, 1)
        else: # v is in B
            if grids[i][j] == '2':
                count2B += 1
                mf.add_edge(v, TT, 1)
            else: # ?
                mf.add_edge(v, T, 1)
mf.add_edge(T, S, MaxFlow.INFFLOW)
mf.add_edge(S, TT, count2A)
mf.add_edge(SS, T, count2B)
flow1 = mf.max_flow(SS, TT)
print('Yes' if flow1 == count2A+count2B else 'No')

AtCoder Beginner Contest 286

4完。5問目の問題E、全く歯が立ちませんでした。ABC285の問題Eは解けた可能性があると思いましたが、今回はできる可能性がなかった。にも関わらず問題Eの正解者は前回の2倍もいて、ぼくの順位も低いです。Ratingは最近横ばいで、伸び悩んでいます。問題Eで使用するワーシャルフロイド法は、以前蟻本で出会った時理解できず、あきらめたアルゴリズムでした。しかし様々なDPの経験を積んだことで、この奇妙な説明も、今回はすんなり頭に入ってきました。なんか早く毎回5完できるようになりたいと焦ってしまっていますが、無理なもんは無理と、謙虚さを取り戻し、リラックスして取り組む姿勢を取り戻そうと思います。今回は問題Eで「ワーシャルフロイド法」を、問題Fで「中国剰余定理」を覚えられたので、解けない焦りよりも、ABCに参加する意義を感じられると良いです。

E - Souvenir

コンテスト終了後、5問目まで解けてる人が1600人くらいいて、ショックを受けました。ぼくは全然解き方の検討がつかなかったというのに！TwitterのABC286タグを見ると「ワーシャルフロイド法」という言葉が流れてました。その名前は知ってます。蟻本の該当箇所を読んで、よくわからなくてスキップしてしまったことを覚えているのです。いずれやろうとアルゴリズムの名前だけメモっていましたが、なんか愚直な感じがするし、O(V^3)だし、使うことあるのかなぁ、と優先度を下げてしまったまま、今に至ります。改めて蟻本を読んでみたところ、普通に理解できました。いや～、わかります。昔わからなかったけど、今はわかるって感慨深いですね。以前スキップしてしまったときは、競技プログラミングを初めて間もなかった頃だったのでしょう。今のぼくは、いくつもの変なDPの問題を解いて経験を積んできたため、DPの考え方に慣れており、自然にこの奇妙な説明が頭に入ってきました。蟻本に、ワーシャルフロイド法は負の辺があっても動作すると、書かれています。これはちょっと謎です。d[i][k]=d[i][k]+d[k][k]としたときに、d[i][k]が更新されてしまうのは、困るのではないかと思いました。単に、ちゃんと終了し、負の閉路が求まる、ということだと解釈しましたが、正しいのでしょうか？ところで、コンテスト時間中、どのように回答したかというと、全クエリに対して、BFSをやりました。QがO(N^2)、BFSがO(N)だからワーシャルフロイド法といっしょでは？とちょっと思ったのですが、勘違いでした。BFSはO(E)=O(N^2)です。なので、ぼくが提出していたやり方だと、計算量がO(N^4)になってしまっていました。解けてる人が多いということは、ワーシャルフロイド法は基礎なんでしょうね。こうやって地道に勉強していくしかありません。 2023-01-22

INF = 1000
N = int(input())
alist = list(map(int, input().split()))
dist = [[INF]*N for _ in range(N)]
value = [[0]*N for _ in range(N)]
for i in range(N):
    dist[i][i] = 0
    value[i][i] = alist[i]
    for j, c in enumerate(input()):
        if c == 'Y':
            dist[i][j] = 1
            value[i][j] = alist[i] + alist[j]
for k in range(N):
    for i in range(N):
        for j in range(N):
            newdist = dist[i][k] + dist[k][j]
            if newdist < dist[i][j]:
                value[i][j] = value[i][k] + value[k][j] - alist[k]
                dist[i][j] = newdist
            elif newdist == dist[i][j] < INF:
                value[i][j] \
                    = max(value[i][j], value[i][k] + value[k][j] - alist[k])
Q = int(input())
for _ in range(Q):
    u, v = map(int, input().split())
    u -= 1
    v -= 1
    if dist[u][v] == INF:
        print('Impossible')
    else:
        print(dist[u][v], value[u][v])

F - Guess The Number 2

異なる素数個でループする数列を作って、Bの情報から余りが求まるから、そこから求めるのかなぁ？というところまでは、なんとなく思いつきます。拡張ユークリッドの互除法を少し前に見ていたので、いける感じはありましたが、「中国剰余定理」を知らなかったので、その先までは進めませんでした。yaketake08さんの実装メモのコードをそのまま使ったらACできました。「中国剰余定理」の典型問題のようです。これは、知ってたら解けてしまいますね。なんてことはなく、素数リストを2、3とすると問題の設定である10^9までカバーできないので、4、9に変えておこなうというところが、ひらめきポイントです。 2023-01-22

def extgcd(a, b):
    if b:
        d, y, x = extgcd(b, a % b)
        y -= (a // b) * x
        return d, x, y
    return a, 1, 0

def remainder(V):
    x = 0; d = 1
    for X, Y in V:
        g, a, b = extgcd(d, Y)
        x, d = (Y*b*x + d*a*X) // g, d*(Y // g)
        x %= d
    return x, d

plist = [4, 9, 5, 7, 11, 13, 17, 19, 23]
print(sum(plist), flush=True)
alist = []
first = 1
for p in plist:
    alist.extend(list(range(first+1, first+p)))
    alist.append(first)
    first += p
print(*alist, flush=True)

blist = list(map(int, input().split()))

idx = 0
amari = []
for p in plist:
    amari.append((blist[idx] + p - idx - 1) % p)
    idx += p
print(remainder(list(zip(amari, plist)))[0], flush=True)

G - Unique Walk

E、Fは知らないアルゴリズムが出てきてしんどかったですが、この問題Gは、比較的易しめのように感じました。Sに属する辺以外をUnion-Findを使ってまとめてしまい、一筆書きできるかどうか？判定すれば良いとわかります。注意点として、最後にグラフを作るところで、同じ辺も追加しなければならないということです。これはサンプルテストケースの1つ目で気づけるようになっていたので、親切でした。「オイラー路」という言葉にも触れる必要があるでしょう。すべての辺を通る閉路を持つグラフを「オイラーグラフ」と呼び、すべての頂点の次数が偶数であることと同値です。閉路でないオイラー路のみ持つものを「準オイラーグラフ」と呼び、次数が奇数であるものがちょうど2つであることと同値です。グラフの次数が奇数である頂点は必ず偶数個です。なぜなら、辺の両側に頂点があるので、次数の合計は必ず偶数であるためです。この問題はオイラーグラフか準オイラーグラフであることを判定する問題なので、次数が奇数の頂点が0個、もしくは2個の場合にYesとなります。次数が奇数の頂点が1個にはなりえないので、<=2をYesの条件とすればよいです。ABC285 Gは、ACに次の土曜の朝までかかりましたが、これは翌日ACできて早めに肩の荷が下りました。このあとARCがあるらしいのですが、どうしよう。 2023-01-22

class Union():
    # 省略
N, M = map(int, input().split())
es = []
for _ in range(M):
    u, v = map(int, input().split())
    es.append((u-1, v-1)) # 0-(N-1)
K = int(input())
xset = {x-1 for x in map(int, input().split())} # 0-(M-1)
union = Union(N)
for i, e in enumerate(es):
    if i not in xset:
        union.unite(e[0], e[1])
from collections import defaultdict
g = defaultdict(list)
for i, e in enumerate(es):
    if i in xset:
        u, v = e
        u = union.find_root(u)
        v = union.find_root(v)
        g[u].append(v)
        g[v].append(u)
oddcount = 0
for v in g:
    if len(g[v]) % 2 == 1:
        oddcount += 1
if oddcount > 2:
    print('No')
else:
    print('Yes')

AtCoder Regular Contest 154

疲れてますが、参加せざるを得ません。笑。2度目、そして2連続のARC参加でした。A、Bの2完でした。問題Aが難しく、1時間くらいかかりました。できたときは嬉しかったです。しかしどうも問題Aを短時間で解いてる人が多い。ARC慣れでしょうか？ぼくは1問しか解いたことがないので、問題Aも大きな壁です。明らかに前回より難しかったですし。そして問題B。ARC153は1完に終わったので、これができれば記録更新。30分くらいで解くことができました。残りの時間、問題Cを考え、考え方までは導くことができましたが実装が間に合わず、時間内の提出に至りませんでした。2度目のARCを経て、やはりARCとABCって全然違うなという印象が強まりました。ARCは、なんらかのアルゴリズムを適用すれば解けるのではなく、自分で考えることの方がメインと感じ、それをおもしろいと思います。昨日のABC286で、Eがワーシャルフロイド法、Fが中国剰余定理というような、どうしようもない感じだったのもあって、なおさらそのような印象が強まりました。あれ？もしかして、ABCって実はおもしろくないのか？

A - Swap Digit

難しいと思うんですが。ACしたときガッツポーズしました。できたコードが気持ちいいです。ARC153 Aよりだいぶ難しいでしょう。でもこれでもARCでは簡単な問題なのでしょう。Aの最上位桁をAU、それ以外をAL、Bの最上位桁をBU、それ以外をBLとすると、かけ算A*Bは100*AU*BU+10*(AU*BL+BU*AL)+AL*BLと表現できます。するとAUとBUをスワップした場合に変化するのはAU*BL+BU*ALの部分だけということがわかります。スワップしたら小さくなるかどうかは引き算をすれば条件が求まります。10の位から最上位の桁まで、順番にスワップするかどうか？決めていけばよいです。確定した値までのAとBを順次更新していき、全桁確定したら、最後に掛け算して答えを求めます。最初に、AとBを各桁の数字をリスト化しましたが、このように実装しました。文字列ってlist関数に渡すとバラバラになるんですね。

A = list(map(int, list(input())))

2023-01-23

import sys
M = 998244353
N = int(input())
A = list(map(int, list(input())))
B = list(map(int, list(input())))
if N == 1:
    print(A[0]*B[0])
    sys.exit()
albig = 0 # 1:a big, 0:equal, -1:b big
if A[N-1] > B[N-1]:
    albig = 1
elif A[N-1] < B[N-1]:
    albig = -1

al = A[N-1]
bl = B[N-1]
keta = 1
for i in range(N-2, -1, -1): # swap i or not
    if albig == 1 and A[i] < B[i] \
        or albig == -1 and A[i] > B[i]:
        A[i], B[i] = B[i], A[i]
    # update al
    keta = keta * 10 % M
    al = (keta * A[i] + al) % M
    bl = (keta * B[i] + bl) % M
    if A[i] > B[i]:
        albig = 1
    elif A[i] < B[i]:
        albig = -1

print(al * bl % M)

B - New Place

これも残り30分くらいのところで解けて、ヨシッと声出ました。SとTの各アルファベットの数が一致していればこの操作を繰り返して同じにできるでしょう。Sの後ろ何文字をそのまま使えるか？調べれば、残りが操作回数ですね。 2023-01-23

import sys
N = int(input())
S = input()
T = input()
counterS = [0]*26
counterT = [0]*26
for c in S:
    counterS[ord(c) - ord('a')] += 1
for c in T:
    counterT[ord(c) - ord('a')] += 1
for i in range(26):
    if counterS[i] != counterT[i]:
        print(-1)
        sys.exit()
posiT = N-1 # position of T
for i in range(N-1, -1, -1):
    c = S[i]
    for j in range(posiT, -1, -1):
        # search c in T
        if c == T[j]:
            posiT = j - 1
            if posiT < 0:
                print(i)
                sys.exit()
            break
    else:
        print(i+1)
        sys.exit()
# i == 0 possible? -> impossible

C - Roller

処理の流れがちょっと複雑になりましたが、ACできました。ぼくの判定ロジックですが、文字列の最初と最後がつながっているとみなして、ランレングス圧縮したときのグループの個数agnum, bgnumを求めます。agnum<bgnumなら操作でグループ数を増やせないのでNoです。そうでない場合は、操作によってグループを損なわずにローテーションさせる余裕があり、かつBのグループをAのグループが含んでいるかどうか？をチェックしています。ランレングス圧縮に、Python標準ライブラリのitertools.groupbyを使えることを知り、初めて利用しました。

akeys = [k for k, _ in itertools.groupby(alist)]
if len(akeys) > 1 and akeys[0] == akeys[-1]:
    akeys.pop()

2023-01-23

import itertools
T = int(input())
for _ in range(T):
    N = int(input())
    alist = list(map(int, input().split()))
    blist = list(map(int, input().split()))
    if alist == blist:
        print('Yes')
        continue
    akeys = [k for k, _ in itertools.groupby(alist)]
    if len(akeys) > 1 and akeys[0] == akeys[-1]:
        akeys.pop()
    bkeys = [k for k, _ in itertools.groupby(blist)]
    if len(bkeys) > 1 and bkeys[0] == bkeys[-1]:
        bkeys.pop()
    agnum = len(akeys)
    bgnum = len(bkeys)
    if agnum < bgnum:
        print('No')
        continue
    # condition of room to move
    if (agnum == bgnum and agnum < N) or agnum > bgnum:
        bb = bkeys*2
        for sta in range(bgnum):
            j = 0
            for i in range(sta, sta + bgnum):
                bk = bb[i]
                while j < agnum and akeys[j] != bk:
                    j += 1
                # akeys[j] == bk or j == agnum
                if j == agnum:
                    # NG : bk was not found
                    break
                # not NG -> check next
                j += 1
                # if j == agnum here and i != sta+bgnum-1,
                # it will go NG break
                # otherwise continue checking next
            else:
                print('Yes')
                break
        else:
            print('No')
    else:
        print('No')
        continue

D - A + B > C ?

なんとなく、問題Dも見てみました。思いつかなかったので解説を見ましたが、かなりおもしろいです。1+1>(1以外の数字)という式は、常にNoなので、N-1回調べればどれが1かわかる。さらに1がわかると、a+1>bがYesならa>b、a+1>bがNoならa<bのため、マージソートで全数字を確定できると。時間内に思いつけたらすごいですし、やはりARCおもしろいなぁという印象が強くなりました。ちなみにぼくは、マージソートが頭に入ってなかったので、思いつけないですし、マージソートの勉強になりました。いつものように、再帰関数ではなくスタックで実装しましたが、そんな必要あるんでしょうか？笑。クイックソートだと最悪計算量がO(N^2)になるので、たぶん競プロではNGなんでしょうね。 2023-01-24

N = int(input())
id1 = 1
for i in range(2, N+1):
    print(f'? {id1} {id1} {i}', flush=True)
    if 'Yes' == input():
        id1 = i
pids = list(range(1, N+1))
stack = [(~0, N), (0, N)] # stack [l,r)
while stack:
    l, r = stack.pop()
    if l >= 0:
        mid = (l + r) // 2
        if l + 1 < mid:
            stack.extend([(~l, mid), (l, mid)])
        if mid + 1 < r:
            stack.extend([(~mid, r), (mid, r)])
    else:
        l = ~l
        mid = (l + r) // 2
        left = pids[l:mid]
        right = pids[mid:r]
        j = 0
        k = 0
        for i in range(l, r):
            if k == len(right):
                pids[i] = left[j]
                j += 1
            elif j == len(left):
                pids[i] = right[k]
                k += 1
            else:
                print(f'? {left[j]} {id1} {right[k]}', flush=True)
                if 'Yes' == input():
                    pids[i] = right[k]
                    k += 1
                else:
                    pids[i] = left[j]
                    j += 1
ans = [0]*N
for i, p, in enumerate(pids):
    ans[p-1] = i + 1
print('!', *ans, flush=True)

AtCoder Beginner Contest 287

4完。問題Eに1時間ほど残っていて、トライ木でいけるだろうとやっていたにも関わらず、REとWAが解決できずに終わりました。今ARC153 Dを解こうとしてしまい、なかなか解けないまま時間が過ぎている状態の上に、ABCでなかなか5完を維持できず、Ratingも伸び悩んで、フラストレーションが半端ないです。かなり危険な状況です。問題Eが解けてないのもダメなんだけど理由がしょーもなくてイライラします。

C - Path Graph?

パスグラフの条件が、N == M+1で、すべての頂点の次数が1か2であれば良いと考えて、最初提出したのですが、パスグラフと、それと非連結の複数の巡回グラフの組み合わせでも、上記条件を満たしてしまうため、NGでした。おもしろいですね。 2023-01-28

E - Karuta

コンテスト時間中、トライ木で粘っていましたが、サンプルテストケースを通過するにも関わらず、WAx14、TLEx11というひどい状況のまま終了時刻を迎えました。トライ木でロジックは間違いないのに、時間内にACできないのはかなりつらいです。最も長いLCPは、ソートして隣を確認するだけで良いとのこと。確かにその通りで、かしこいです。これを思いつかなければなりません。まずはそれで解いてみます。 2023-01-28

N = int(input())
slist = [(input(),i) for i in range(N)]
slist.sort(key=lambda x:x[0])
def check_LCP(a, b):
    minlen = min(len(a[0]), len(b[0]))
    for i in range(minlen):
        if a[0][i] != b[0][i]:
            break
    else:
        return minlen
    return i
ans = [0]*N
for i in range(N):
    lcp = 0
    if i > 0:
        lcp = max(lcp, check_LCP(slist[i-1], slist[i]))
    if i < N-1:
        lcp = max(lcp, check_LCP(slist[i], slist[i+1]))
    ans[slist[i][1]] = lcp
for i in range(N):
    print(ans[i])

トライ木でのWAですが、どうも同じ文字列が複数含まれているようで、ムカつきますが仕方ないです。トライ木の文字列の終端ノードに同じ単語数のカウンターを追加して対処しました。TLEは、再帰呼び出し回数の上限が原因でした。しょーもないですが、まだまだダメということで、改善しながら続けていくしかありません。トライ木も地道に改善します。 2023-01-28

import sys
sys.setrecursionlimit(10**6)
class Trie():
    def __init__(self, c=''):
        self.c = c
        self.children = {}
        self.wordcount = 0
    def add(self, idx, word):
        if not self.c: # this is root
            if word[0] not in self.children:
                self.children[word[0]] = Trie(word[0])
            self.children[word[0]].add(0, word)
        elif idx == len(word) - 1: # end ow word
            self.wordcount += 1
        else: # add next char
            if word[idx+1] not in self.children:
                self.children[word[idx+1]] = Trie(word[idx+1])
            self.children[word[idx+1]].add(idx+1, word)

N = int(input())
root = Trie()
slist = []
for i in range(N):
    S = input()
    slist.append(S)
    root.add(0, S)

for s in slist:
    trie = root.children[s[0]]
    if len(s) == 1 and trie.children:
        print(1)
        continue
    # len(s) > 1
    ans = 0
    for i in range(len(s)):
        if i < len(s)-1: # 終端ではない
            if trie.wordcount:
                ans = i+1
            for c in trie.children:
                if c != s[i+1]:
                    ans = i+1
                    break
            trie = trie.children[s[i+1]]
        else: # 終端 -> break
            if trie.children or trie.wordcount > 1:
                ans = i+1
            break
    print(ans)

上のトライ木が遅くて時間制限ギリギリなのが気に入らないので、リストで実装してみました。以前から気になっていたのでやっただけで、ライブラリとして残すには直したいところがいろいろありますが、残しておきます。しかし処理時間が半分くらいになりましたが、まだ他の提出者より遅いです。他の人どうやってるんだろうか？ 2023-01-29

ちょっと書き換えて、終端フラグの代わりに、ノードが単語に使われてる回数を持たせるようにしました。こうすれば、2回以上使われていればそこまでは共通プレフィックスってことで、コードがスッキリします。が、別に速くはなってません。 2023-01-29

class Trie:
    def __init__(self, size):
        self.n = size
        self.nodes = [0]*(size*27)
        self.newnode = 1
    def print(self):
        for i in range(self.n):
            print(i, self.nodes[27*i:27*(i+1)])
    def add(self, word):
        '''word should be splitted integers'''
        node = 0
        for c in word:
            node_next = self.nodes[node*27+c]
            if not node_next:
                self.nodes[node*27+c] = self.newnode
                node_next = self.newnode
                self.newnode += 1
            node = node_next
            self.nodes[node*27+26] += 1
    def count_prefix(self, word):
        res = 0
        node = 0
        for i, c in enumerate(word):
            node = self.nodes[node*27+c]
            if self.nodes[node*27+26] > 1:
                res = i+1
        return res
N = int(input())
slist = []
trie = Trie(500001)
for _ in range(N):
    S = [ord(c)-ord('a') for c in list(input())]
    slist.append(S)
    trie.add(S)
for s in slist:
    print(trie.count_prefix(s))

F - Components

「木DP」というらしいです。少し前これまでに出てきたDPをざっと見直して、いろいろなパターンが頭に入ったかなとちょっと期待したのですが、すぐに甘かったことが判明しました。「木DP」とは。これを知らずに導けたらすごいです。さらになんとなくやり始めてしまったARC153 Dで「桁DP」というものに出会いました。新しいDPが連続で出てきますが、まだまだ出てくるのでしょうか？子の計算がすべて終わってから親の計算をする必要があるため、帰りがけでそれを行っています。子要素から先に計算するような順列を生成してそれに従って処理するというのでも良さそうです。いずれにせよ、Pythonでは解説のような再帰関数方式は使えませんので。さて、頂点vを根とする部分木で、連結成分の数がj個で、vを選択するかどうか0/1というキーで組み合わせ数をDPするようです。確かにできるなぁと思ってやり始めましたが、子の計算結果をまとめるところをどのように実装すればよいか？困ってしまいました。結局どうやっているかというと、子の結果をまとめるのではなく、親に順番にマージしていってます。「子の結果をまとめるか？親に順番にマージするか？」なんかただの言い換えなのですが、この言い換えによって、自然に計算できるのですから、不思議としか言いようがありませんが、プログラミングあるあるのような気がします。あとは、dp0[v]とdp1[v]のサイズは同じになるように進めることでシンプルに処理することに注意。それと、連結成分の数って抜けないっぽいですね。つまり、連結成分が3個の場合はあるけど、2個の場合はない、みたいなことはありえないです。消せば2個になるので。なんかこういった微妙な事実も、初めてだと気づいてなかったりするので重要です。まあ仕方ないんじゃないかなと思っています。dp0の初期値[1,0]とdp1の初期値[0,1]は、頂点1個だけ見た場合の、連結成分0個の場合と1個の場合の数です。選ぶか選ばないか？しかないので、初期値はこのようになります。 2023-02-06

N = int(input())
M = 998244353
g = [[] for _ in range(N)]
for _ in range(N-1):
    a, b = map(int, input().split())
    a -= 1
    b -= 1
    g[a].append(b)
    g[b].append(a)
dp0 = [[1, 0] for _ in range(N)] # not select i
dp1 = [[0, 1] for _ in range(N)] # select i
parent = [-2]*N
stack = [-1, 0] # 0 is root
parent[0] = -1
while stack:
    cur = stack.pop()
    if cur >= 0:
        for next in g[cur]:
            if next != parent[cur]:
                parent[next] = cur
                stack.extend([~next, next])
    else:
        cur = ~cur
        # gather results
        for next in g[cur]:
            if next == parent[cur]:
                continue
            len_cur = len(dp0[cur])
            len_next = len(dp0[next])
            length = len_cur + len_next - 1
            temp0 = [0]*length
            temp1 = [0]*length
            for i in range(len_cur):
                for j in range(len_next):
                    temp0[i+j] += dp0[cur][i] * (dp0[next][j] + dp1[next][j])
                    temp0[i+j] %= M
                    temp1[i+j] += dp1[cur][i] * dp0[next][j]
                    temp1[i+j] %= M
                    if i+j-1 > 0:
                        temp1[i+j-1] += dp1[cur][i] * dp1[next][j]
                        temp1[i+j-1] %= M
            dp0[cur] = temp0
            dp1[cur] = temp1
for item in zip(dp0[0][1:], dp1[0][1:]):
    print(sum(item) % M)

G - Balance Update Query

典型問題寄りですが、やり方に気づいても、このコード長だと、ぼくは実装が間に合わないかなぁ、と想像します。勉強にもなりました。「クエリ先読み」という言葉を、聞いたことはあるけど使ったことがなく、なんだろうなぁと思っていたのですが、この問題で初めて使うことができて理解しました。フェニック木を使うために「座圧」していますが、クエリを最後まで処理する中でありうるカードの得点を、すべて把握しなければ「座圧」できないため、「クエリ先読み」しました。自然な発想ですね。フェニック木を2つ使うパターンはABC276 Fでも出てきましたので、改めて確認しておきたいです。この問題を通じてフェニック木に関する気づきもありました。1つは、フェニック木のインデックスは1からですが、prodの引数に0を入れたら0が返ってくるので、気にせず0を渡せるなぁということ。この性質により、2分探索のところで、余計な分岐をしなくてすみました。一方、addの方のインデックスに0入れたら無限ループしますね。もう1つは、prod_range(i,j)で範囲クエリーの関数もあれば便利だなぁということで追加しました。また、2分探索をあまりちゃんと勉強してないというか、苦手意識がありますが、何度か使って慣れてきて良かったです。処理の流れをちゃんと整理する必要のある問題ですが、提出1回目でACできました。 2023-02-07

class BIT():
    def __init__(self, n):
        self.n = n
        self.sums = [0]*(n+1)
    def add(self, i, input):
        while i <= self.n:
            self.sums[i] += input
            i += i&-i
    def prod(self, i):
        '''return 0 if i == 0'''
        res = 0
        while i > 0:
            res += self.sums[i]
            i -= i&-i
        return res
    def prod_range(self, i, j):
        return self.prod(j) - self.prod(i)

N = int(input())
alist = [0]*N # points
blist = [0]*N # count
points_set = set()
for i in range(N):
    a, b = map(int, input().split())
    alist[i] = a
    blist[i] = b
    points_set.add(a)
Q = int(input())
qlist = []
for _ in range(Q):
    q = list(map(int, input().split()))
    if q[0] == 1:
        q[1] -= 1 # 0 index
        points_set.add(q[2]) # new point
    elif q[0] == 2:
        q[1] -= 1 # 0 index
    qlist.append(q)

n_bit = len(points_set) # num of point kinds
points_list = sorted(list(points_set))
points_comp = {p:i+1 for i,p in enumerate(points_list)}
points_list = [0] + points_list # 1 index
bit_num = BIT(n_bit)
bit_pnt = BIT(n_bit)
count_card = 0
for i in range(N):
    a, b = alist[i], blist[i]
    count_card += b
    idx = points_comp[a]
    bit_num.add(idx, b)
    bit_pnt.add(idx, a*b)
for q in qlist:
    if q[0] == 1:
        p = alist[q[1]]
        n = blist[q[1]]
        p_new = alist[q[1]] = q[2]
        idx = points_comp[p]
        bit_num.add(idx, -n)
        bit_pnt.add(idx, -n*p)
        idx = points_comp[p_new]
        bit_num.add(idx, n)
        bit_pnt.add(idx, n*p_new)
    elif q[0] == 2:
        p = alist[q[1]]
        n = blist[q[1]]
        n_new = blist[q[1]] = q[2]
        count_card += n_new-n
        idx = points_comp[p]
        bit_num.add(idx, n_new-n)
        bit_pnt.add(idx, (n_new-n)*p)
    else:
        n = q[1]
        if n > count_card:
            print(-1)
            continue
        elif n == count_card:
            print(bit_pnt.prod(n_bit))
            continue
        lowbound = count_card - n
        l = 0
        r = n_bit
        while l + 1 < r:
            m = (l+r)//2
            if lowbound <= bit_num.prod(m):
                r = m
            else:
                l = m
        ans = bit_pnt.prod_range(r, n_bit) +\
            points_list[r] * (n - (count_card - bit_num.prod(r)))
        print(ans)

AtCoder Regular Contest 155

疲れて眠いですが、出れるなら出るしかない！という気持ちで参加しました。ARCの参加は3回目ですが、問題Aがこれまでで一番難しく、（ARC153、ARC154と、問題Aはどんどん難しくなりました。）初めての0完に沈みかけました。途中頭が働いてなかったですし、あ～疲れてたし出なかったら良かったなぁ、とか考えてしまってましたが、なんと、残り5分でACできました。順位はぴったり賞のちょうど1000位。今回は、ほとんど0完だったらしく、ギリギリで1問解いただけで、これまででベスト2の順位です。やっぱり出て良かったです。Ratingも初めて1000を超えました。

ARC155でRating1000超え

ちょうど1000位！

A - ST and TS Palindrome

そういえば、最近回文の問題を別のところでも見た気がしますが、回文のアルゴリズムがあったと思うんですが、あれをまだ勉強してないのでドキッとします。しかし知らないと解けないというような状況には陥ってません。最初、KがNと比べて比較的小さいところだけ調べて、あぁいけそうだなぁと思ったのですが、2つ目のサンプルテストケースが通りません。KがNに対して大きいと、別扱いが必要になってくるのです。この状況をなかなか整理できず、終了時刻がせまってしまいました。最後、ふとACできて、声出ました。良かったぁ。1完と0完では天と地ですから。 2023-01-29

最初if K>Nとか、if K>2*Nとか条件分岐していましたが、条件分岐しなくても良いようなので、条件分岐を消しました。 2023-01-30

T = int(input())
def check(s, l, r):
    while l < r:
        if s[l] != s[r]:
            return False
        l += 1
        r -= 1
    return True
for _ in range(T):
    N, K = map(int, input().split())
    S = input()
    amari = (K-N) % (2*N)
    if amari > N:
        amari = 2*N - amari
    if check(S, 0, amari-1) and check(S, N-amari, N-1)\
        and S[amari:] == S[:N-amari]:
        print('Yes')
    else:
        print('No')

AtCoder Beginner Contest 288

残念ながら3完でした。3完はしばらくなかったので、ショックです。が、どうも今回の問題Dは難しめだったらしく、4完できた時点でほぼ過去最高の順位、パフォーマンスになっていたようです。そういうこともあるのを受け止めなければなりません。問題Cも簡単じゃないと感じましたが、みんなやたらと早く解けていて（なんで？）、そのせいでぼくの順位は低くなってしまっており、入水が遠のくようでつらいです。

C - Don’t be cycle

閉路を無くすために削除する辺の本数の最小値。ぎょっとなったのですが、一瞬で解いてる人が多く（なぜ？）、こんなの基本なんですかねぇ。連結成分からDFSで木を作り、見つかった閉路をカウントしていきました。閉路って見つかった個数1つずつしかなくせないので、問題に最小値と書いてあるけど全部カウントすればよいです。両側からカウントするので、最後2で割っています。解説では頂点数Xの連結成分において、閉路ができない（=木の）辺の数はX-1であることを利用し、連結成分の数から答えを求めていました。考え方を覚えておく価値がありますね。 2023-02-04

N, M = map(int, input().split())
g = [[] for _ in range(N)]
for _ in range(M):
    a, b = map(int, input().split())
    a -= 1
    b -= 1
    g[a].append(b)
    g[b].append(a)
graphid = 0
usedin = [0]*N # graph id, 0 is not used
parent = [-2]*N # -2 not decided -1 root's
ans = 0
for v in range(N):
    if not usedin[v]:
        graphid += 1 # next graph id
        stack = [v]
        usedin[v] = graphid
        parent[v] = -1
        while stack:
            cur = stack.pop()
            for next in g[cur]:
                if not usedin[next]:
                    stack.append(next)
                    usedin[next] = graphid
                    parent[next] = cur
                # already used in graph
                elif next != parent[cur]:
                    ans += 1
print(ans//2)

D - Range Add Query

解けませんでした。難しい！コンテスト中に考えられたのは、とりあえず1つのクエリに対してO(N)で答えることまでで、それがQ個あるのでO(NQ)、そこから改善できませんでした。解説では、階差数列を作ると書かれていました。なるほど、Range Addをすると、階差数列が変化するのは、K離れた入り口と出口だけであり、操作時に両側のプラマイは0になることがわかります。操作で和が変化しないのであれば、和が0になっている必要があり、和が0になっていれば操作によってすべて0にできることもわかります。Aの先頭に0を追加してから階差数列を作り、添字をKで割った余りごとに累積和を計算しておく…とちょっとややこしいので、階差数列の話は触れておく程度にして、わかりやすかった方法で解きます。添字をKで割った余りごとに、Aの累積和を求めます。区間[l,r]で添字をKで割った余りごとの和がすべて一致していることが、操作によって0にできる条件です。まず、なぜ添字をKで割った余りごとの和がすべて一致している必要があるのか？これは操作によってK幅の区間全部に+Cするか-Cするのですから、和の変化が同じです。なので、1つ0になれば全部0になっていなければならないです。すごいひらめきだ！というわけで、1つ0にすればよいわけですが、左から順に0でなければ0になるように操作することを繰り返せばよいです。最後の操作で[r-K+1]に対して操作することで、必ず1つのグループを0にできることがわかり、先程の説明通り、他もすべて0になります。こんなのコンテスト中に解けたらなぁ。Range Add->mod Kみたいな定石ですかね。 2023-02-05

N, K = map(int, input().split())
temp = [0]*K
sum_modk = [0]*N
for i, a in enumerate(map(int, input().split())):
    temp[i%K] += a
    sum_modk[i] = temp[i%K]
Q = int(input())
for _ in range(Q):
    l, r = map(int, input().split())
    l -= 1
    r -= 1
    ls = [0]*K
    rs = [0]*K
    for i in range(K):
        rs[(r-i) % K] = sum_modk[r-i]
        ls[(l-1-i+K) % K] = 0 if l-1-i < 0 else sum_modk[l-1-i]
    val = rs[0] - ls[0]
    for i in range(1, K):
        if rs[i] - ls[i] != val:
            print('No')
            break
    else:
        print('Yes')

E - Wish List

問題Dで行き詰まった間、こちらをしばらく考え、一筋縄でいかないと感じてDに戻っていました。実際解説を読んでもいまいちピンとこず、難しかったです。解説は、正しい説明のために用意した数式で書かれており、直感的ではなくて何を言ってるかわからない、ということが結構あるように思います。だからといって直感的に書くって何？という話で、理解する側ががんばって自分なりの説明にたどり着くというプロセスが必要、なのでしょう。解説に書いてあるcostという式や、「この下界は達成可能です。 実際、「現時点での購入費用がその下界 (1) を達成している商品」の中で番号が最大のものを買うという行動を繰り返すことで達成できます。」という説明、読んでも頭に入ってこず、自分なりに考え直して理解しました。この問題におけるDPでは、i番目について計算するときに、i-1番目までに何個買うか？をキーとして使っています。買うと決めるだけで、すでに買ったわけではないのがこのDPの難しいところです。買う順番によって値段のCの部分が変化してしまうからです。i-1まででx個買う場合、iを買う時点でそのx個のうち何個先に買ったかによってCの値が決まります。0個からx個のうち何個買ってからiを買うのか？Cの値が0からxまでの場合で変化するのですが、これが、一番安く買えるというのが結論です。自力で気づくのかなり難しいと感じているんですが、みんなどういう思考手順で、しかも短時間で、たどりつけるんですかね？そうなってないと難しいよなぁ、みたいなところから勘でたどりつくんでしょうか？うーん。自分なりの説明を書きます。買う商品の番号が小さい順に、a,b,c,d,…だったとします。aは実はいつ買ってもコストはCaです。aより小さい番号は買わないのですから、買う時点で必ずa番目なのです。つまり、aはいつ買ってもいいことがわかります。bを買うときaを購入済みであればCb-1、aを未購入であればCbです。重要なのは、aの影響しか受けないということです。bより小さい番号で買うのはaだけですから。しかしaはいつ買っても同じと先程わかりましたので、aとbの購入順は自由に決めてよく、Cb-1とCbの小さい方を選べるのです。cはどうでしょうか？aとbを買うタイミングによってCc-2、Cc-1、Ccの3通りが考えられますが、もっとも小さくなるように、aとbの順序に対して、cを買う順序を決められます。よって、i番目を買う時にCi、Ci-1、Ci-2、Ci-3、…の中で最小コストは確定できることがわかります。むずかしい。むちゃくちゃ難しいと思うんですが。気づける人すごすぎるな。改めて先に引用した解説の文章は、一体正しいことを言ってるのでしょうか？CのRange Minimumが必要なので、dpといっしょにcminも逐次更新していますが、この実装もちゃんと整理しないと混乱に陥ります。ところで、Python勢の中で最速タイの207msです。いつも時間制限に苦しめられているので、他の人より速いとうれしいです。 2023-02-05

N, M = map(int, input().split())
A = [0] + list(map(int, input().split()))
C = [0] + list(map(int, input().split()))
Xset = set(map(int, input().split()))
dp = [10**14]*(N+1)
cmin = [10**14]*(N+1) # cmin[i] i個買わない場合
dp[0] = 0
count_bought = 0
for i in range(1, N+1):
    a = A[i]
    for j in range(1, i+1):
        cmin[j] = min(cmin[j], C[i])
    buy = i in Xset
    for j in range(count_bought, i)[::-1]:
        if buy:
            dp[j+1] = dp[j] + cmin[i-j] + a
        else:
            dp[j+1] = min(dp[j+1], dp[j] + cmin[i-j] + a)
    if buy:
        count_bought += 1
    if count_bought == M:
        break
print(min(dp[M:]))

F - Integer Division

雰囲気的にDPだろうなぁ。i番目をまでの合計値は、Σ(dpk + X[k+1:i])だなぁ。と、そこまでいっても、最後まで詰められない。解けたい問題です。式変形するとこんなにシンプルなDPにたどり着けます。これをひらめけないの、本当にくやしいです。むちゃくちゃいい問題ですね。 2023-02-06

M = 998244353
N = int(input())
X = [int(c) for c in input()]
dp = X[0]
sum = 1 + X[0]
for i in range(1,N):
    dp = (sum * X[i] + 10 * dp) % M
    sum = (sum + dp) % M
print(dp)

G - 3^N Minesweeper

また解説を見ても最初ピンとこなかったですが、サウナで考えてたらわかりました。問題の条件から、近い位置にある爆弾の数がわかっているわけです。ある位置のi桁目が0だった場合、その近い位置にある爆弾の位置は、i桁目が0か1であることがわかります。（他の桁のことは後で考えましょう。）同様に、i桁目が1なら近い位置はi桁目が0か1か2、i桁目が2なら近い位置はi桁目が1か2です。それぞれa個、b個、c個だったとしましょう。b-cを計算するとi桁目が0である個数に絞り込めることがわかります。b-aでi桁目が2、a+c-bでi桁目が1に絞り込めます。すべての桁で同様に絞り込めば、全桁確定した個数が求まるというわけです。むずかしい！あたおか。えげつない気がするのですが。これをコンテスト中にひらめくってどうなってんでしょうか？ぼくもいつかできるのでしょうか？？？orange #3進数 2023-02-07

N = int(input())
alist = [a for a in map(int, input().split())]
for i in range(N):
    pow3i = 3**i
    for j in range(3**N):
        if j // pow3i % 3 == 0:
            x, y, z = j, j+pow3i, j+2*pow3i
            alist[x], alist[z] = alist[y]-alist[z], alist[y]-alist[x]
            alist[y] -= alist[x] + alist[z]
print(*alist)

AtCoder Beginner Contest 289

4完でした。問題DをPythonでやったところ、制限時間2秒に対してTLEx3、どうしても高速化方法が思いつかないので、APG4bで学びたてのC++で同じロジックで書き直したところ、69msでACできました。どんだけ速度違うんでしょう？しかし解説を見ると、もっと速いロジックがあることがわかり、それであればPythonでも84msでした。しかし下手くそな実装のC++にまだ負けてんじゃん。下手くそでもむちゃくちゃ速いC++、使うしかねぇと再認識した今日です。C++で書き直している間に1000位くらい下落して、パフォーマンスが下がりまくり、全然レーティングが伸びません。つらいです。伸び悩むとやめたくなります。

D - Step Up Robot

C++コードも載せてますが、同じ方法でPythonでやると、2秒の制限に間に合いません。C++で書けるようになってて良かったです。このPythonの実装を思いつかないのは反省点です。 2023-02-11

import sys
input = sys.stdin.readline
N = int(input())
alist = list(map(int, input().split()))
M = int(input())
bset = set(map(int, input().split()))
X = int(input())
dp = [0]*(X+1)
dp[0] = 1
for i in range(X+1):
    if i in bset:
        continue
    for a in alist:
        if i-a >= 0 and dp[i-a] == 1:
            dp[i] = 1
            break
print('Yes' if dp[X] else 'No')

// C++
int main() {
    int N, M, X;
    cin >> N;
    vector<int> A(N);
    for (int i = 0; i < N; i++) {
        cin >> A.at(i);
    }
    cin >> M;
    set<int> B;
    for (int i = 0; i < M; i++) {
        int b;
        cin >> b;
        B.insert(b);
    }
    cin >> X;
    set<int> S;
    S.insert(0);
    while (!S.empty()) {
        int cur = *begin(S);
        S.erase(cur);
        for (int a : A) {
            int next = cur + a;
            if (next == X) {
                cout << "Yes" << endl;
                return 0;
            }
            if (B.find(next) == B.end() && next < X) {
                S.insert(next);
            }
        }
    }
    cout << "No" << endl;
}

E - Swap Places

思いつきませんでした。解けてる人が多いですが、普通に難しいと感じています。高橋君と青木君の位置を合わせて状態とみなすことで、NxNの盤面を移動する問題になります。うーん、これみんな見えるのかぁ。難しいなぁ。その盤面上の最短経路を求めるので、BFSをします。DFSじゃないので、注意。 2023-02-11

from collections import deque
T = int(input())
for _ in range(T):
    N, M = map(int, input().split())
    clist = [0] + list(map(int, input().split()))
    g = [[] for _ in range(N+1)] # 1 indexed
    for _ in range(M):
        u, v = map(int, input().split())
        g[u].append(v)
        g[v].append(u)
    dist = [[-1]*(N+1) for _ in range(N+1)]
    q = deque([(1,N)])
    dist[1][N] = 0
    found = False
    while q:
        t, a = q.popleft()
        dcur = dist[t][a]
        for nt in g[t]:
            for na in g[a]:
                if dist[nt][na] == -1 and clist[nt] != clist[na]:
                    if nt == N and na == 1:
                        print(dcur + 1)
                        found = True
                        break
                    q.append((nt,na))
                    dist[nt][na] = dcur + 1
            if found:
                break
        if found:
            break
    if not found:
        print(-1)

F - Teleporter Takahashi

コンテスト時間中に考えられませんでしたが、こういうの時間内に解きたいなぁ。A<BだとAとA+1を使ってワープすることで、どちらの方向へも2ずつ移動することができます。つまり、2の倍数離れた任意の位置に移動できます。奇数回目は反対側に飛んでるので、どうすればよいでしょうか？1回目で移動した位置から2ずつ移動できると考えると、奇数回目も2の倍数離れた任意の位置に移動できることがわかります。A=BやC=Dの場合について、ちゃんと整理すれば解けます。 2023-02-11

import sys
Sx, Sy = map(int, input().split())
Tx, Ty = map(int, input().split())
A, B, C, D = map(int, input().split())
def move_even(start, end, a):
    if end > start:
        return [a,a+1]*((end-start)//2)
    return [a+1,a]*((start-end)//2)
def move_odd(start, end, a):
    start = 2*a-start
    return [a] + move_even(start, end, a)
if (Tx-Sx) % 2 == 1 or (Ty-Sy) % 2 == 1:
    print('No')
    sys.exit()
if A == B:
    if C == D:
        if (Sx,Sy) == (Tx,Ty):
            print('Yes')
        elif (2*A-Sx,2*C-Sy) == (Tx,Ty):
            print('Yes')
            print(A, C)
        else:
            print('No')
        sys.exit()
    else: # C < D
        if Sx != Tx and 2*A-Sx != Tx:
            print('No')
        else:
            print('Yes')
            if Sx == Tx:
                ylist = move_even(Sy, Ty, C)
            else:
                ylist = move_odd(Sy, Ty, C)
            ans = [[A, y] for y in ylist]
            for a in ans:
                print(*a)
        sys.exit()
if C == D:
    if A < B:
        if Sy != Ty and 2*C-Sy != Ty:
            print('No')
        else:
            print('Yes')
            if Sy == Ty:
                xlist = move_even(Sx, Tx, A)
            else:
                xlist = move_odd(Sx, Tx, A)
            ans = [[x, C] for x in xlist]
            for a in ans:
                print(*a)
        sys.exit()
# C < D and A < B
print('Yes')
xlist = move_even(Sx, Tx, A)
ans = [[x, C] for x in xlist]
ylist = move_even(Sy, Ty, C)
ans.extend([[A, y] for y in ylist])
for a in ans:
    print(*a)

G - Shopping in AtCoder store

「Convex Hull Trick」というらしいです。1次関数の集合があるとき、あるxに対して最大値は？みたいな問題を解くために、どの領域でどの関数が最大か？求めておく方法です。聞いてみると、ぼくも中高生だったころなら自力で思いついてたかもなぁ、と思え、なんか残念に感じます。1次関数の交点とかも何年も求めていないと、久々の再開にドキッとしてプレッシャーを感じます。やってみると簡単なんですけれど。ふ～、できて良かったぁみたいにホッとする自分がいます。P=C+Bで購買意欲Bの人が買いますので、Bが大きい値から小さい値に降りていくと、買ってくれる人の人数がどんどん増えていくことがわかります。このBと人数Nのセットリストは、Cと無関係で固定だなぁとわかります。PNの最大値を求めれば良いので、1つの商品ならO(N)で求められることがわかりますが、この問題は商品数Mがでかいので、毎回計算してられません。ここで、売り上げは、PN=(C+B)N=CN+BNと表せます。NとBNの全リストに対して、Cを変数とした1次関数が作られることがわかり、「Convex Hull Trick」こと「CHT」によって、各区間でCN+BNが最大となる1次関数を求めておくことにより、各Cに対してO(log(N))で売り上げの最大値を求めることができます。改めて、なんか高校生の頃の自分ならこのやり方が見えた可能性あるのでは？とちょっと思います。1次関数の集合を処理するということまでわかれば、この実装は導けました。今回は傾きが小さい順に1次関数を追加できるのでやりやすいですが、順番が自由に決められない場合は、もう少し処理が複雑になりそうです。 2023-02-13

from collections import defaultdict
import bisect
N, M = map(int, input().split())
b2n = defaultdict(int)
for b in map(int, input().split()):
    b2n[b] += 1
count = len(b2n)
b2n_sort = sorted(b2n.items(), key=lambda x:x[0])
n = [0]*(count+1) # index count is dummy
bn = [0]*count
for i in range(count)[::-1]:
    n[i] = b2n_sort[i][1] + n[i+1]
    bn[i] = b2n_sort[i][0] * n[i]
n = n[:count][::-1]
bn = bn[:count][::-1]
posi = [0.0]
line = [0]
for i in range(1, count):
    while True:
        posi_new = (bn[line[-1]]-bn[i]) / (n[i]-n[line[-1]])
        if posi[-1] < posi_new:
            posi.append(posi_new)
            line.append(i)
            break
        else:
            posi.pop()
            line.pop()
            if not posi:
                posi.append(0.0)
                line.append(i)
                break
ans = []
for c in map(int, input().split()):
    idx = bisect.bisect_right(posi, c)
    idx -= 1
    ans.append(n[line[idx]] * c + bn[line[idx]])
print(*ans)

AtCoder Regular Contest 156

AB2完、そして873位でパフォーマンス1490と、3ヶ月ぶりに過去最高を更新できました。現在、典型90を順番にやっている最中なので、終了後は問題Cまでとしておこうと思います。

A - Non-Adjacent Flip

操作にある「裏返す」というのが、表のものを裏にすることのみを指すのか？それとも裏を表にするものも含むのか？サンプルケースでは前者しか出てこず、問題を読んでて曖昧に感じました。一旦前者を前提に提出してWAx2を確認し、後者もありと認識して解きました。と言っても後者が必要になるケースは、コインが4枚で、その中の隣り合った2枚が表を向いている場合に限られ、その場合は特別な条件分岐をします。 2023-02-18

T = int(input())
for _ in range(T):
    N = int(input())
    S = list(map(int, list(input())))
    count1 = 0
    for i in range(N):
        if S[i]:
            count1 += 1
    if count1 == 2:
        neighbor = False
        for i in range(N):
            if S[i] == 1:
                if S[i+1] == 1:
                    neighbor = True
                break
        if neighbor:
            if N == 3:
                print(-1)
            elif 0 <= i-2 or i+3 < N:
                print(2)
            else:
                print(3)
        else:
            print(1)
    elif count1 % 2 == 0:
        print(count1 // 2)
    else:
        print(-1)

B - Mex on Blackboard

難しく感じましたし、時間内にACできてうれしかったです。考えてるうちにひらめきました。mexとして次に追加できる数字は、黒板に0が書かれていない場合は0のみ、0が書かれている場合は「0から連続する最大の数字+1」までの任意の数字です。追加する値の最大値ごとに場合分けすれば、排他的にカウントできますので、そのようにします。最大値を更新していって、元々書かれていたAに到達するたびに、追加できる値は一気に増えるので、そのことを考慮して計算すればよいです。ぼくの回答では、Aが0を含んでいた場合だけちょっと下手な場合分けになってしまいました。 2023-02-18

N, K = map(int, input().split())
M = 998244353
COUNT_MAX = N + K
fact = [0]*(COUNT_MAX+1)
invfact = [0]*(COUNT_MAX+1)
fact[0] = 1
for i in range(1, COUNT_MAX+1):
    fact[i] = fact[i-1] * i % M
invfact[COUNT_MAX] = pow(fact[COUNT_MAX], M-2, M)
for i in range(COUNT_MAX-1, 0, -1):
    invfact[i] = invfact[i+1] * (i+1) % M
invfact[0] = 1
def choose(n, r):
    return fact[n] * invfact[r] * invfact[n-r] % M

alist = sorted(set(map(int, input().split())))
lena = len(alist)
count = 0
watch = 0
ia = 0
ans = 0
while count < K:
    if ia == 0 and alist[0] == 0:
        while ia+1 < lena and alist[ia+1] == alist[ia]+1:
            ia += 1
        # iaは連続するaの最後
        watch = alist[ia]
        ia += 1 # 次を指しておく
    elif ia < lena and alist[ia] == watch+1:
        while ia+1 < lena and alist[ia+1] == alist[ia]+1:
            ia += 1
        # iaは連続するaの最後
        watch = alist[ia]
        ia += 1 # 次を指しておく
        count += 1
    else: # watch is not in alist
        count += 1
    ans += choose(K-count+watch, watch)
    ans %= M
    watch += 1
print(ans)

C - Tree and LCS

コンテスト時間中に20分残っていて、類似度1にするのだろうと思い、枝ごとにリバースするような方針を考えていましたが、これでは類似度1にできないことがわかり、思いつかないので解説を見ました。木の頂点のうち、次数1のものを2つ選びスワップして消す、という処理を繰り返すことで常に類似度1のPを求めることができます。特定のパスの両端をスワップすると、どちらかを部分列として選択した時点で、類似度1が確定しますので、1より大きくしようと思うと、部分列の要素として選べないことになり、類似度の計算はそれを除いた部分だけ調べればよくなります。そうやって2つずつ末端の頂点を消していき、最後1つ残れば明らかに類似度1、2つ残ってスワップしても類似度1より大きくならないため、この方法でPを生成すればよいとわかります。解説では、末端頂点の数を見ていましたが、ぼくの頭の中では頂点数をwhile文の条件にした方が自然に思え、そのように実装しています。アルゴリズムを説明するロジックが難しいです。 2023-02-19

N = int(input())
G = [set() for _ in range(N+1)]
for _ in range(N-1):
    u, v = map(int, input().split())
    G[u].add(v)
    G[v].add(u)
leaves = []
for v in range(1, N+1):
    if len(G[v]) == 1:
        leaves.append(v)
P = list(range(N+1))
nodecount = N
while nodecount >= 2:
    v1 = leaves.pop()
    v2 = leaves.pop()
    P[v1], P[v2] = v2, v1
    nodecount -= 2
    if not nodecount:
        break
    n1 = G[v1].pop()
    G[n1].remove(v1)
    if len(G[n1]) == 1:
        leaves.append(n1)
    n2 = G[v2].pop()
    G[n2].remove(v2)
    if len(G[n2]) == 1:
        leaves.append(n2)
print(*P[1:])

AtCoder Beginner Contest 290

5完でした。問題Eはひらめきを求められる良い問題でした。ひらめいてからも、整理して実装するのに時間がかかり、残り3分くらいでACという緊張感のある展開でしたが、とにかくこれが時間内に解けたことで、ACと表示されたのを見てホッとしたのと同時に、かなりの充実感を得ることができました。そして初めて800位以内に入り、795位、パフォーマンスも過去最高の1573と、今週は2日連続で記録更新できました。

2日連続で過去最高パフォーマンス

D - Marking

NとDの最小公倍数進んだところで0に戻ってきますね。最初にx+1が必要になるのは必ず0に戻ってきたときです。0以外で先にかぶるわけがありません。 2023-02-19

T = int(input())
for _ in range(T):
    N, D, K = map(int, input().split())
    n = N
    d = D
    while n:
        d, n = n, d % n
    # d is gcd
    rot = (K-1) // (N // d)
    amari = (K-1) % (N // d)
    print(D*amari%N + rot)

E - Make it Palindrome

回文チェックに必要なすべてのペアで比較を行うと、計算量がO(N^2)となってしまい間に合わないので、どこを減らせるか考えました。少し眺めると、明らかに同じペアで何度も比較しているところは見つかります。しかし、同じペアを1回比較するとしてもO(N^2)で、全く意味がないです。どうするか？絵を描いてうなってるうちに、なんかふと、調べる全ペア数から一致しているものを引けばよいのでは？と天の声が聞こえてきましたw数列の中で一致しているものをまとめておけば、どかっとカウントできますね。異なることは比較しないとわからないですが、一致しているものをまとめておけば、その中のどのペアも一致していることが、一気にわかります。それからもまあ大変で、コンテストの時間ギリギリまで粘ってやりきりました。ACできてよかったです。考えてる時に描いた絵も貼っておきます。ちなみに、全体から引くことでO(N^2)を回避するのは、ABC282 Dで経験して印象に残っています。その時はTLEを解消できませんでした。 2023-02-19

ABC290 Eのメモ

from collections import defaultdict, deque
N = int(input())
TOTAL = 0
for x in range(1, N):
    TOTAL += ((x+1) // 2) * (N-x)
alist = list(map(int, input().split()))
adict = defaultdict(list)
for i, a in enumerate(alist):
    adict[a].append(i)
samecount = 0
for idxlist in adict.values():
    if len(idxlist) < 2:
        continue
    dq = deque(idxlist)
    while len(dq) >= 2:
        l = dq[0]
        r = dq[-1]
        if l == N-1-r:
            samecount += (2*len(dq)-3)*(l+1)
            dq.popleft()
            dq.pop()
        elif l < N-1-r:
            samecount += (len(dq)-1)*(l+1)
            dq.popleft()
        else:
            samecount += (len(dq)-1)*(N-r)
            dq.pop()
print(TOTAL-samecount)

F - Maximum Diameter

なにやら難しそうですが、木の辺の数はN-1、次数の和は2倍で2N-2、この和を満たしていれば木を作れます。また、直径は次数が2以上の頂点数+1であることがわかるので、それを元に、求める数式を書くことができます。Sum[(choose(n,k) * choose(n-3,k-1) * (k+1)),{k,1,n-2}]ですね。なぜなら、2以上の値がk個ある場合の数は、まずN個からk個選び（つまりchoose(N, k)）、次数はすべて1以上なので、次数の和2N-2のうち、残りのN-2をK箇所に割り振りますが、このK箇所は次数2以上なので、K個使いますので、残りはN-2-Kを、K箇所に割り振ります。その組み合わせはchoose(N-2-K+K-1, K-1) = choose(N-3, K-1)です。で、kを1からN-2まで変化させて合計すればよいです。しかし和を求めるところでO(N)になってしまい、クエリーも20万個あるので間に合いません。しかしO(1)で求まるはずと思えば、WolframAlphaに突っ込んで式変形してもらえばいけそうです。実際、突っ込んだら返ってきました。(N-1)*N^2*(N^2-3)*(2N-4)! / (N!)^2らしいです。最初これでACしました。しかしちょっとずるいですね。そして解説を理解しました。競プロにおいて、非常に重要な考え方を含んでいると思われ、とても勉強になる解説です。先程も説明したように、求める値は、全パターンにおけるK+1の合計です。1の方は全パターン数になるので、横に置いておいて、Kの合計を求める必要があります。Kは2以上の要素の個数でしたので、全パターンでの2以上の要素の個数の和を求める必要があります。ここで見方を転換します。それぞれのパターンでの2以上の要素の個数ではなく、頂点iが2以上になる回数の和と考えます。パターン別にカウントしていたのを、頂点別にカウントするように見方を変えるのです。すると全頂点に対して対称性があるので、頂点1の次数が2以上になる回数xN」と言い換えることができます。頂点1の次数が2以上になるパターンの数は、N-2のうち1つを頂点1に割り当てておき、残りのN-3をN頂点に割り振る方法の数なので、choose(N-3+N-1, N-1)で求めることができます。よってまとめると、choose(2*N-3, N-1) + N * choose(2*N-4, N-1)という式を手計算で導くことができます。パターン別でカウントしていたのを頂点別でカウントするように見方を変え、対称性を使って整理する。これがこの問題の重要な学びですね。対称性といえば、最近ABC284 Gがありました。ABC284 Gは計算量がO(N)でした。改めて見直しても難しいですが、数え上げの考え方は通じるものがあります。 2023-02-23

M = 998244353
T = int(input())
Ns = [int(input()) for _ in range(T)]
COUNT_MAX = max(Ns) * 2
fact = [0]*(COUNT_MAX+1)
invfact = [0]*(COUNT_MAX+1)
fact[0] = 1
for i in range(1, COUNT_MAX+1):
    fact[i] = fact[i-1] * i % M
invfact[COUNT_MAX] = pow(fact[COUNT_MAX], M-2, M)
for i in range(COUNT_MAX-1, 0, -1):
    invfact[i] = invfact[i+1] * (i+1) % M
invfact[0] = 1
def choose(n, r):
    return fact[n] * invfact[r] * invfact[n-r] % M
for N in Ns:
    if N == 2:
        print(1)
    else:
        print((choose(2*N-3, N-1) + N * choose(2*N-4, N-1)) % M)

G - Edge Elimination

X以上頂点数があってできるだけ小さい木を取り出し、Xになるまでできるだけ大きな木を削っていく。という方針だとNGでした。最初にできるだけ小さい木を取り出すと、逆に回数が増えることがあるようです。深さdの頂点数をT(d)とします。たとえばX = T(x) - (k-1)*T{1} - kだったとすると、T(x)を取り出すのに1回、T(1)を削るのにk-1回、k個削るのにk回、合計2k回でXになります。元の木がT(x+2)だった場合、T(x+1)をk-1回削り、T(x)をk-1回削り、T(2)を1回削ればXになります。合計2k-1回でさっきより少ないです。というわけで、最初に残す木の大きさは全探索します。もっとスマートに最初に残す木の大きさがわかればうれしいですが、わかりませんでした。DはK=2で最大60くらいにしかならないので、bisectを使ってるのはちょっと大げさかもしれません。とはいえ、bisectを使う時に結構慎重に考えて時間がかかってるので、一瞬で書けるように使い方を整理したいです。bisect_left(a,x)は、「x以上の最小値のインデックス」が返ってきます。xがaの最後の値より大きい場合は、len(a)が返ってきます。bisect_right(a,x)は、「xより大きい最小値のインデックス」が返ってきます。xがaの最後の値以上の場合は、len(a)が返ってきます。書いてみるとそれだけですかね…。leftが小、rightが大なので、小さいか大きいかの違いだと錯覚してる節がありますが、実はどっちも大きい値を見つけるのは変わらないんですよね。「left : x以上の最小インデックス、right : xより大きい最小インデックス」この合言葉で、今後思考の効率化ができるかもしれません。 2023-02-23

import bisect
T = int(input())
for _ in range(T):
    D, K, X = map(int, input().split())
    sums = [1]
    powk_cur = 1
    # 0, 1, 2, ..., D
    for d in range(1, D+1):
        powk_cur *= K
        sums.append(sums[-1] + powk_cur)
    ans = 10**18
    idx_upper = bisect.bisect_left(sums, X)
    for root in range(idx_upper, D+1):
        cur_ans = 0
        if root != D:
            cur_ans += 1
        left = sums[root] - X
        while left:
            idx_lower = bisect.bisect_right(sums, left) - 1
            cuts = left // sums[idx_lower]
            left %= sums[idx_lower]
            cur_ans += cuts
        ans = min(ans, cur_ans)
    print(ans)

AtCoder Regular Contest 157

A、Bの2完でした。BをACしたのが22:58:49www。ペナルティ7回からの残り1分でなんとかACという、緊張感のある展開でした。前回、ABC290も残り3分で5完でしたし、心臓に悪いです。ACしたときはウホホホホと言って床に倒れ込みました。なんたって残り1分ですから。そりゃあ全身脱力するでしょう。問題Cをコンテスト終了後に自力ACできたので、なんか惜しい気持ちです。ABC277 Gで同様の手法を初めて見たときは驚きましたが、典型と言えるのでしょうね。

A - XXYYX

おもしろいです。状態遷移の図を描くと、XYの次にXYが出てくる前に、必ずYXを経由する必要があります。YXの次にYXが出てくる前に、必ずXYを経由する必要があります。よって、XYの数BとYXの数Cの差は1以内である必要があります。XXとYYは好きなだけ連続で作れますが、BもCも0だった場合は、XXとYYの間を行き来できないので、XXの数Aまたは、YYの数D、どちらかが0である必要があります。このことには初回で気づけました。 2023-02-25

ARC157 Aの状態遷移図

B - XYYYX

コンテスト残り1分でACしました。この問題の状況を整理するのは難しいです。最後はXのみの場合、Yのみの場合で、Nが小さい時の場合分けを修正しながら何度も提出するという、手に汗握る展開でした。それは置いといて、全体的な考え方を述べると、まず、ランレングスに分解する。両側をYに挟まれた連続するXを短い順にソート。ここから優先的にYにフリップしていきます。なぜなら、両側をYに挟まれていると、最後のフリップではYXY->YYYとなり、YYが一気に2つ増えて得だからです。できるだけYXY->YYYを発生させようと思うと、連続するXの数が少ない順にやったほうがいいです。Yに挟まれているXがなくなったら、Yに挟まれてないX（つまり、文字列の両端）をフリップしていきます。この時はフリップする度にYYは1つずつしか増えません。全部Yになって、まだK回フリップしていなかったら、YをXにフリップする必要があります。これは元々Xに挟まれていなかったY（つまり、文字列の両端）から優先してフリップしていきます。Xに挟まれていたYをフリップすると、YYが一気に2つ減ってしまうからです。文字列の両端のYがなくなってもまだK回フリップしていなかったら、内側のYをXにフリップしていきます。この時、連続するYのフリップで、最初の1回だけYYが2つ減ります。つまり、できるだけ減らないようにするには、連続するYが長い順にフリップしていったほうが良いです。なので、Yのランレングスは長い順にソートしてから操作していきます。 2023-02-25

Submission #39199136 - AtCoder Regular Contest 157

C - YY Square

スコアは個数の2乗、ということで、ABC277 Gを思い出しました。n^2=2*nC2+nC1と変形することで、それまでに現れたYYを2つ選択する場合の数と1つ選択する場合の数を求める問題に言い換えられるのです。1つも選択しない場合の数は経路数になります。これもちゃんと更新し続けなければならないことに注意です。 2023-02-25

M = 998244353
H, W = map(int, input().split())
grids = [[c=='Y' for c in input()] for _ in range(H)]
dp0 = [[0]*W for _ in range(H)]
dp1 = [[0]*W for _ in range(H)]
dp2 = [[0]*W for _ in range(H)]
for i in range(1, H):
    dp0[i][0] = 1
    dp1[i][0] = dp1[i-1][0]
    if grids[i][0] and grids[i-1][0]:
        dp1[i][0] += 1
    dp2[i][0] = dp2[i-1][0]
    if grids[i][0] and grids[i-1][0]:
        dp2[i][0] += dp1[i-1][0]
for j in range(1, W):
    dp0[0][j] = 1
    dp1[0][j] = dp1[0][j-1]
    if grids[0][j] and grids[0][j-1]:
        dp1[0][j] += 1
    dp2[0][j] = dp2[0][j-1]
    if grids[0][j] and grids[0][j-1]:
        dp2[0][j] += dp1[0][j-1]
for i in range(1, H):
    for j in range(1, W):
        dp0[i][j] = dp0[i][j-1] + dp0[i-1][j]
        dp1[i][j] = dp1[i][j-1] + dp1[i-1][j]
        dp2[i][j] = dp2[i][j-1] + dp2[i-1][j]
        if grids[i][j]:
            if grids[i][j-1]:
                dp1[i][j] += dp0[i][j-1]
                dp2[i][j] += dp1[i][j-1]
            if grids[i-1][j]:
                dp1[i][j] += dp0[i-1][j]
                dp2[i][j] += dp1[i-1][j]
        dp0[i][j] %= M
        dp1[i][j] %= M
        dp2[i][j] %= M
print((2*dp2[H-1][W-1] + dp1[H-1][W-1]) % M)

AtCoder Beginner Contest 291

5完でした。現在、うまくいけば入水できるかもしれない位置につけているので、入水を目指して臨んでました。今回入水したかった理由は、2月最後であること、入緑に3ヶ月かかったので、今回入水できるとまた3ヶ月でちょうどよいこと、競プロを始めてからちょうど半年の節目であること、そろそろこのnoteの文字数が29万字の制限を超えそう（現在278000字）なので、その前に入水したいことなど、いろいろと入水したい条件が重なっているんですよねぇ。今回入水したらきれいにまとまったんですが、そうはうまくいかないもの。結構できた？と思ったら1488位でパフォーマンス1242。残念ながら、今回簡単だったようで伸びませんでした。Ratingは+10で1161。4連続水パフォなのは喜ばしいですが、割と凹みます。解けなかった問題Fも解けなければならなかったなぁと反省です。とはいえ、問題Eも問題Fもぼくにとっては難しく感じるので、実力通りであることは素直に受け止められます。

E - Find Permutation

そんなに簡単じゃないと思ったんですが、2000人解いてますね。これでも典型なのでしょうか？順序が確定するためには、iとi+1の比較はすべて知っていなければなりません。ちょっと考えてそう気づきました。「入力に矛盾しないAが存在する」という制約があるので、確実にトポロジカルソートできます。そしてその結果が一意に確定する順序である必要があるため、トポロジカルソート後に、すべての隣同士の比較が提示されているかどうかをチェックして解きました。 2023-02-26

F - Teleporter and Closed off

コンテスト時間に解けず、悔しいです。1とN、両側からダイクストラで各都市への最短距離を求めておき、通ってはいけない都市は、それをまたぐようなパターンを全探索すれば最短経路が求められます。典型90の013 - Passingも、両側からダイクストラをして解く問題でした。あれは、自力でひらめいて解けて喜んでたんです。でも「都市kを通る」という制限から「都市kを通らない」という制限に変わっただけで、思いつけませんでした。結構凹みますね。思いつきたかったです。典型90 013とほとんど同じなので、ここでは「都市kをまたぐ」ところの処理だけコードを載せておきます。これだけなんですよねぇ。 2023-02-26

と思ったんですが、dpっぽく距離を求められるので書き直したのを載せておきます。典型90 013の回答からコピーしてきて提出するのが最速回答方法だったのは間違いないです。 2023-02-27

INF = 10**6
N, M = map(int, input().split())
G = [[] for _ in range(N+1)]
Gr = [[] for _ in range(N+1)]
for i in range(N):
    for j, c in enumerate(input()):
        if c == '1':
            a, b = i+1, i+j+2
            G[a].append(b)
            Gr[b].append(a)
dist_1n = [INF]*(N+1)
dist_1n[1] = 0
for v in range(2, N+1):
    for prev in Gr[v]:
        dist_1n[v] = min(dist_1n[v], dist_1n[prev] + 1)
dist_n1 = [INF]*(N+1)
dist_n1[N] = 0
for v in range(1, N)[::-1]:
    for prev in G[v]:
        dist_n1[v] = min(dist_n1[v], dist_n1[prev] + 1)
ans = []
for k in range(2, N):
    ans_cur = INF
    for x in range(max(1, k-M+1), k):
        for y in G[x]:
            if y > k:
                ans_cur = min(ans_cur, dist_1n[x]+dist_n1[y]+1)
    ans.append(-1 if ans_cur == INF else ans_cur)
print(*ans)

G - OR Sum

畳み込みとのこと。1度だけnumpyで解いたことがあるだけで、ちゃんとライブラリ化もできていないので、この機会にちゃんと履修したいと思います。いや、ACLでやるべきでしょうか？せっかくなので今回はPythonでのライブラリ化とACLを使ってのAC、両方やりたいと思います。 2023-02-26

などといいながらまずはnumpyでAC。この問題を畳み込みで解けるっていう発想がすごいですね。最初WAx20になってしばらく原因がわかりませんでした。何を勘違いしていたかというと、上の桁から貪欲に取っていくと一番大きな値になると思ってました。よく考えたら上位桁の1を一番多くしなくても、次の桁で巻き返すなんて普通にあります。そんなことになかなか気づけ無いのですから思い込みって怖いです。Python勢のWAを見ていると、同じミスをして直したっぽい人が他にも2人いました。 2023-02-28

# fftコード省略

N = int(input())
alist = [np.ones(2*N, dtype=np.int64) for _ in range(5)]
blist = [np.ones(N, dtype=np.int64) for _ in range(5)]
for i, a in enumerate(map(int, input().split())):
    keta = 0
    while a:
        if a&1:
            alist[keta][i] = alist[keta][i+N] = 0
        a //= 2
        keta += 1
for i, b in enumerate(map(int, input().split())):
    keta = 0
    while b:
        if b&1:
            blist[keta][N-i-1] = 0
        b //= 2
        keta += 1
convolves = [convolve(alist[keta], blist[keta])[N-1:2*N-1] for keta in range(5)]
ans = 0
for i in range(N):
    ans = max(ans, sum([(N - convolves[keta][i])*(2**keta) for keta in range(5)]))
print(ans)

AtCoder Beginner Contest 292

ABCDFの5完。コンテスト時間中に問題Fを解いたのは初めてかもしれません。しかし問題Eは解けず、入水は寸止めでお預けとなりました。つらい！あとこのnoteの文字数がもう限界です。入水してこのnoteを完成とし、次のnoteに移りたいんですよね。

入水寸止めのABC292

E - Transitivity

単純有向グラフという言葉がよくわからず、いつも「単純有向グラフとは」みたいなの付いてるのに今回はないんかい！と思いました。諦めてFを解いて、その後Gを見て無理そうだったので、Eに再チャレンジし、残り10秒くらいで提出したらTLEx2でした。iでループを回して、u->i->vとなるu,vを結び続けるという処理だったので、O(N^3)でした。え？TLEx2だけ？と思ってC++でもやってみましたが、同じくTLEx2でした^^;Pythonコノヤロウではなく、O(n^3)がアウト。当たり前ですね。正解は、全頂点から到達できる点を調べて、結ぶだけでした。確かにこの操作で結ばれるのは、ある点から到達できる点だけです。これは気づけなければなりませんでした。計算量は、DFSはエッジ数Wで終わるのでO(NW)。全頂点からDFSなのに、O(NW)で済むというのは盲点で、やったこともなかったので、選択肢に挙がりませんでした。勉強になります。 2023-03-04

F - Regular Triangle Inside a Rectangle

初めて時間中に解けたFと思います。幾何が好きです。 2023-03-04

G - Count Strictly Increasing Sequences

桁DPだし区間DPだし、遷移の整理が難しいし、激ムズです。解説理解できず、長考しました。いざACしてしまうと苦しみをうそのように忘れてしまうのですが、どうやったら自力で導けるのか？考察するのが大事だと思います。同じ問題出されても忘れてるでしょう。こういうきつい問題で、処理時間が、Python勢最速の288msっていうのはうれしいですね。4次元DPであり、k桁目のi-j区間がn以上の数字のみで単調増加である組み合わせの数を調べます。すると、kは小さい順、nは大きい順に調べるとすると、k桁目がn以上の数字で単調増加の場合の数は、n+1以上の数字で単調増加の場合に加え、iからいくつかがnに一致し、かつ、すでに調べ終わっているk-1桁までが0以上の数字で（つまりすべての）単調増加である場合の数と、残りはすでに調べ終わっているn+1以上で単調増加の場合の数の積を計算すれば良いとわかります。 2023-03-05

MOD = 998244353
N, M = map(int, input().split())
slist = [list(reversed(list(input()))) for _ in range(N)]
klist = [[(-1 if '?' == slist[i][k] else int(slist[i][k])) for i in range(N)] for k in range(M)]
dp = [[[[0]*M for _ in range(N)] for _ in range(N)] for _ in range(10)] # k j i n
# init first digit
for i in range(N): # when n = 9
    if klist[0][i] == 9 or klist[0][i] == -1:
        dp[9][i][i][0] = 1
for n in range(9)[::-1]: # n = 8 ~ 0
    for i in range(N):
        for j in range(i, N):
            dp[n][i][j][0] = dp[n+1][i][j][0]
            if klist[0][i] == n or klist[0][i] == -1:
                if i == j:
                    dp[n][i][j][0] += 1
                else: # i < i+1 <= j < N
                    dp[n][i][j][0] += dp[n+1][i+1][j][0]
for k in range(1, M):
    for i in range(N): # when n = 9
        for j in range(i, N):
            if not (klist[k][j] == 9 or klist[k][j] == -1):
                break
            dp[9][i][j][k] = dp[0][i][j][k-1]
    for n in range(9)[::-1]: # n = 8 ~ 0
        for i in range(N):
            for j in range(i, N):
                dp[n][i][j][k] = dp[n+1][i][j][k]
                for ok_n in range(i, j):
                    if not (klist[k][ok_n] == n or klist[k][ok_n] == -1):
                        break
                    dp[n][i][j][k] += dp[0][i][ok_n][k-1] * dp[n+1][ok_n+1][j][k]
                    dp[n][i][j][k] %= MOD
                else:
                    if klist[k][j] == n or klist[k][j] == -1:
                        dp[n][i][j][k] += dp[0][i][j][k-1]
                        dp[n][i][j][k] %= MOD
print(dp[0][0][N-1][M-1] % MOD)

AtCoder Beginner Contest 293

入水に王手がかかって最近力んでますが、敗退しました。Ratingは少し下がりました。寸止めでなかなか入水できないのは結構メンタルに効きます。最近典型90を強迫観念に突き動かされてハイペースで進めていたり、今日も直前にABC276 Exを苦労してACしたり、疲れているのはすごく感じます。何もしない日が欲しいです。

D - Tying Rope

ACしたのが81分だったので、時間かかりました。面倒な方針を立ててしまい、反省点が多いです。両端点を頂点としてグラフを作りましたが、よく考えたらロープを頂点にしてもいいです。あとミスったのが、頂点を順番に見て、辿っていって戻ってきたら閉じていると判定しようとしたのですが、閉じていない場合、反対方向も辿っておくのを忘れていて最初バグっていました。汚いコードになりました。よく考えたら端点だけ先に調べて残ったものは閉じているはずなのでもう一度ループを回すとか、シンプルにやる方法はありました。 2023-03-11

E - Geometric Progression

これで良かったのか。気づけなくて不覚。やっぱ疲れている？ 2023-03-11

A, X, M = map(int, input().split())
if A == 1:
    print(X%M)
else:
    print((pow(A, X, M*(A-1))-1) // (A-1))

F - Zero or One

しばらく考えて何もひらめかないので公式解説見ました。Nをd桁で表せる基数は1つしかない、ということを説明しているのですが、エグいです。これどうやったら気づけるのか？3桁以上のd桁で基数bで表す最大値Σ(i:0,d-1)b^iに対し、(b+1)^(d-1)の方が確かに大きい。よって、基数bのd桁の数字と、基数b+1のd桁の数字の範囲は全く重なっていない。よって、d桁のものはあっても1つ。すごい。 2023-03-11

コード書いたら大変だった。d桁のときのxを決める処理のところでちょっとハマった。x^(d-1)がnを超えるところまでxをインクリメントして、超えたら1個戻るみたいな。111..11を超えた場合は調べず次の桁数に進むとか。こういうの悩まずに書けるとうれしい。 2023-03-12

T = int(input())
ans = []
for _ in range(T):
    N = int(input())
    if N == 2:
        ans.append(1)
        continue
    cur = 2
    d = 3
    while True:
        n = N
        x = max(1, int(N**(1/(d-1))) - 1)
        while n >= x**(d-1):
            x += 1
        x -= 1
        if x == 1:
            break
        if n > (x**d-1)//(x-1):
            d += 1
            continue
        while n:
            if n % x > 1:
                break
            n //= x
        else:
            cur += 1
        if x <= 2:
            break
        d += 1
    ans.append(cur)
print(*ans, sep='\n')

G - Triple Index

「Moのアルゴリズム」というらしい。[l,r]に関するクエリで、l、rを1ずらした値を求める計算量がO(1)のときに、クエリを先読みして良い順序にしてから処理することで高速化する。lをN/√Qの幅ごとにまとめて、その中でrは昇順とする。でもrは昇順降順交互にすればより移動が少ないかもしれないので、一応そうしておく。最初やってみたらTLEに。1ずつずらして、最後に、3つ以上ある数字の個数ごとにnC3を求めて出力していたせいだった。3つ以上ある数字の個数でO(N)がかかってしまう。ずらす度にnC3を更新していけば、答えは常に求まった状態を維持できる。n-1からnに増えたとき、nC3は、n-1C2増える。nからn-1に減るときの減り方も同じ。ずらすたびに、足したり引いたりして最新の状態をキープするとTLEを解消できた。こういうの大事。幅をN/√Qにするのは、lをまとめる幅をBとおいて計算量を見積もるとQB+N^2/Bとなり、最小になるのはこれの微分が0になるときという条件で考えると、確かにN/√Qが良さそうとわかる。 2023-03-12

lrlist = [(*map(int, input().split()), q) for q in range(Q)]
sublen = int(N / (Q**0.5))
if sublen < 1:
    sublen = 1
def func_sort(x):
    global sublen
    group = x[0]//sublen
    return (group, x[1] if group%2==0 else -x[1])
lrlist.sort(key=func_sort)

AtCoder Regular Contest 158

A、1完。入水ならず。今週は、入水間近となっていたRatingを、土日で下げてしまいました。疲れた。精神的にきついです。

跳ね返されて入水ならずのARC158

A - +3 +5 +7

80分使って解きました。難しかったです。解説の3を-1、5を0、7を+1に置き換えて総和が変化しない方法には気づかず、途中で2で割ったり、3で割ったりしながらACしました。解説の方法すげぇ。ぼくの解法では、考える過程で3の倍数じゃないとダメと出てきたんですよね。開設の方法だと、総和変わらないから最初に気づいてしまう。 2023-03-12

Submission #39679448 - AtCoder Regular Contest 158

B - Sum-Product Ratio

40分はあったのですが、正しいやり方を証明しようとして結局解けませんでした。終了間際に、0付近と最大と最小のいくつかを取ってきて、3数の組み合わせを全部調べればいけるだろうと、証明せずに実装し始めましたが、間に合わず。結局それでいけたようです。ねじ込めたら入水できたかも。脱力。。。解説の説明は、x1,x2を固定すると1/x3が最大と最小のものが計算値の最大と最小に対応するので、x1,x2がなんであれ、x3は最大最小の3つ以内に入ると。そして、x3がなんであれ、x1もx2も最大最小3つ以内に入るはずです。なので、テキトーにやってもACできたのです！こういうのある程度正しそうと思った時点でぶっこみたいですね。運命を左右します。 2023-03-12

C - All Pair Digit Sums

writerのmaspyさんによると典型とのことです。まず、足し算する前の全桁を足しておく。足し算時に桁上りが発生すると、上の位が1増加、現在の位は10減ることになります。よって桁上がり1回につき、桁の和は9減少することになります。10^dに桁上りするのは、10^dで割った余り同士を足して10^d以上になる場合です。桁上りは絶対に1以下です。これが割と面食らうけど確かにそうで、この問題を解くための肝になる事実。10^d以上になるペアを、ソートしてからしゃくとり法でカウントすればいいです。無駄な処理がまだあるかなぁと思いながら提出しましたが、現在Python勢2位の484msというのがうれしいです。数列を文字列sのまま受け取り、桁の合計をsum(map(int, s))としました。文字列もmapもイテレーターっぽく使うとこうなります。また、桁を上から順番に降りていく部分、alist = list(map(lambda x: x % cur, alist))として、10^dで割った余りの数列を作りました。全体的に良さそうです。 2023-03-12

N = int(input())
slist = input().split()
sumdigi = 2 * N * sum([sum(map(int, s)) for s in slist])
alist = list(map(int, slist))
dnum = len(str(max(alist)))
carry = 0
for d in range(dnum)[::-1]:
    cur = 10**(d+1)
    alist = list(map(lambda x: x % cur, alist))
    alist.sort()
    r = N-1
    for l in range(N):
        need = cur - alist[l]
        while r >= 0 and alist[r] >= need:
            r -= 1
        carry += N - 1 - r
print(sumdigi - carry*9)

D - Equation

解説の[3]以降は今読む気力がないですが、おもしろいのでやりました。「同次式の変数をすべてt倍すると、式の値がt^n倍になる」っていうのは頭に入れておきたいですね。乱択も使ったことがなく、初めてでした。全体的にひらめける気がしないですが、おもしろいです。 2023-03-13

def f(vals, n, p):
    res = sum(vals) % p
    res *= sum([pow(v, n, p) for v in vals])
    res %= p
    res *= sum([pow(v, 2*n, p) for v in vals])
    return res % p
def g(vals, n, p):
    return sum([pow(v, 3*n, p) for v in vals]) % p
T = int(input())
import random
for _ in range(T):
    n, p = map(int, input().split())
    while True:
        vals = random.sample(range(1, p), 3)
        fret = f(vals, n, p)
        gret = g(vals, n, p)
        if fret == 0 or gret == 0:
            continue
        t = gret * pow(fret, p-2, p) % p
        print(*sorted([v*t%p for v in vals]))
        break

AtCoder Beginner Contest 294

5完も、ワースト9のパフォーマンスでRatingを大きく下げ、入水ならず。今回、実はマンションの上の階からの騒音で不動産屋に電話するなどイライラして集中できませんでした。5冠でも786位から2716位と順位が広く分布するので、邪魔されて遅くなるだけでも命取りです。ぼくは競プロの問題を読むのが苦手で、結構集中力を要します。特に問題Dの文章が意味不明気味だったので、騒音のせいで、大きく順位を落としたと思います。入水を意識しているせいで神経質なので、イライラは頂点に達しました。

D - Bank

イベント1なくても結果変わらないし、何言っとんねん、みたいな。イライラ。。。 2023-03-19

E - 2xN Grid

ソートして同じ数字の範囲をまとめて、いもす法で2つ重なってるところを見つけるというやり方をしましたが、前から順に調べればよく、遠回りだったようです。 2023-03-19

F - Sugar Water 2

解けませんでした。解説を見ると、ベースとなる考え方は気づけるべきと思え、くやしいです。横軸を水、縦軸を砂糖と、混ぜるのはベクトルの和で、傾きが濃度なので～偏角ソート？みたいなことを考えてO(N^2)=25億通りの組み合わせを処理できませんでした。これ、2分探索で解くとのこと。気づけません。ある濃度を超えるために必要な砂糖の量は、計算できます。すると2つの砂糖水を混ぜたときに超えるかどうかは、足りない分を補って超えるかどうか？確認すればよいです。すごい。NとM区別せずに計算量書きます。濃度Xを決めます。O(N)で高橋君の足りない砂糖量を計算します。O(N log(N))でソートします。青木君のそれぞれの砂糖水に対して、濃度Xに足りない量を計算し、砂糖量が十分な高橋君の砂糖水の数を2分探索で数えながら合計しますO(N log(N))。濃度Xを精度が十分になるまで2分探索します。誤差10^-9とあり、100回くらい？になるらしい。結局100N log(N)で解けます。 2023-03-20

G - Distance Queries on a Tree

蟻本に同じ問題が載ってるらしいと聞いて確認したら載ってました。しかもなぜか付箋が。次読もうとしてたのかもしれません。不思議な偶然…。「オイラーツアー」はよく聞くし、勉強しようと思ってたのですが、内容は確認しつつもちゃんとやれてませんでした。LCAもせっかくなので「オイラーツアー」を使います。RMQのセグ木に位置情報も必要ですが、やってみると特に難しくはないですね。最初、サンプルは通るのに他のケースほとんどWA。セグ木のクエリでLRの大小逆になってたり[)とすべきところ[]にしてたり、ミスしまくってました。「オイラーツアー」を初めて使ったからこうなるし、通すの大事です。ABCを通じて与えられる良い機会に感謝。現在Python勢最速の1186ms、出せました。 2023-03-21

Submission #39916015 - AtCoder Beginner Contest 294

Housewife Wind (POJ No.2763) in 蟻本

AtCoder Beginner Contest 295

4完。Rating横ばい。30回の節目、半年の節目、3月最後の節目、順調に入水できずに通り過ぎ、メンタル壊死。それにしても回答遅いから1744位、パフォーマンス1177に沈んでいるものの、Eを解けば400位に入っており、最高パフォーマンス更新で多分入水してた。今回みたいなコンテストはチャンスであり、Eが解けないというのがもったいないし悲しすぎる。間に合わせて感動の入水というのが最高シナリオだった。直前でいま一歩伸びないのは、もやもやが続いてしまう。

D - Three Days Ago

DPでやったら重かったがPythonでも通せた。2^10未満の整数でi番目までに0から9までの数字が奇数個か偶数個かを表現すると、同じ数字の間は全部偶数個とわかる。 2023-03-25

E - Kth Number

残った時間がんばって愚直に書いていたが、提出間に合わず。解説の式変形が知らなかったし賢い。数字の期待値 = Σ(K x Kになる確率) = Σ(K以上になる確率)、というように変形できるという。1以上になる確率で1,2,3,…になる確率が求まり、2以上になる確率で2,3,…になる確率を加えることになるので、2が2回加えられる。kはちゃんとk回加えられる。賢い。この式変形により、見通しが良くなって、コーディングが楽でミスも減る。0を置き換えるのは、K以上が何個でK未満が何個というのでちゃんとループしないと排他的にカウントできないので注意。 2023-03-25

F - substr = S

条件分岐がしんどそうで、コンテスト終了後にもやる気が出なかったが、ようやくAC。思った通りしんどい。これも「主客転倒」という。各数字にSがいくつ含まれるか数えるのではなく、Sが特定の位置にある数を数える。Sが0から始まっている場合の条件分岐を、なかなか整理しきれない。こういうのは最初から短いコードを書こうとせず、まずは冗長と感じても必要以上に場合分けした方が、整理が進むような気がする。あと、R以下からLより小さいものを引かなければならないところ、L以下を引いてしまっていて、WAx28。これもなかなか何をミスってるかわからなかった。これを時間内にACできる人たち、普通にすごいと思う。 2023-04-04

G - Minimum Reachable City

かなりおもしろい問題だと思う。まず有向グラフの作り方。N-1本で、i本目のエッジはi以下の頂点から頂点i+1に伸びている。まず、これはツリーになると気づく必要がある。で、1つ目のクエリでグラフに変更が入るが、変な条件がついている。uからvに辺を追加、ただしvから辺を辿ってuに到達できることが保証される。最初からあるツリーの辺は親から子へしか行けないようになっている。よって、vからuに行けるということは、vからLCAまでは、すでに強連結成分になっているということを意味するとわかる。強連結成分をまとめていくということでUnion-Findが適切だろう。2つ目のクエリで必要となる最小値は代表点に持たせておけばよい。vからuに行ける状態で、uからvにつなぐと、強連結成分が拡大する。そのときに追加すべき頂点をUnion-Findで追加していく処理をする。どうやるんだろう？と最初悩むけど、変な条件をよく見ると、できるじゃん！となる。 2023-04-06

AtCoder Beginner Contest 296

5完。1069位、パフォ1400。低迷してたので、ホッとするけど横ばいは横ばい。入水できないからしんどいのが続く。エイプリルフールに入水したかった。6完の壁が厚い。まぐれであと1問解ければ入水なんだよなぁ。今回無証明提出でいける可能性もあったし。

D - M<=ab

4ペナで30分かかった。とりあえず、aは√Mまででいいから100万、bは割れば求まるので、計算量が収まる。 2023-04-01

E - Transition Game

実行時間117msは、終了後の現在0:23でもPython勢最速。うれしい。ループを検出するために、ループ以外を削除するが、inputがない頂点を消せるだけ消して、残ったのをカウントした。効率的だったっぽいな。 2023-04-01

F - Simultaneous Swap

転倒数の偶奇性でいけるんだろうなぁと推測して、無証明で提出しようとしてたけど、同じ値が複数ある場合に対応しきれず、力尽きた。正解しかけてたとも言えるけど、考えきれてないのだからしかたない。この説明がわかりやすい。集合が一致し、置換の偶奇性が一致しているか、同じ値があれば、一致させられる。こんな風にシンプルに考察しないとなぁ。ついでに偶置換、奇置換について考えておきたい。置換回数の偶奇性は一意である。数列差積が置換した2つだけ入れ替えたように変化するので、置換の度にプラス、マイナスが入れ替わることから、証明できる。典型の066、089でも転倒数が出てきた。バブルソートでは1回の置換で転倒が1つ解消されるので、置換回数と転倒数が一致する。偶奇一意性から、転倒数を数えれば、偶置換か奇置換かわかる。この問題では、考察よりABの偶奇が一致していれば揃えられる。 2023-04-01

G - Polygon and Points

問題G、そんなに自力ACできたことなさそうだけど、これはいけた。難しくはないと思う。ただめちゃめちゃ面倒だったし、実行速度はPython勢でうしろから5番目。効率悪そう。tupleのリストに対してbisectするの良くなさそう。やはりそうで、2267msから1429msになって真ん中くらいの速度がでた。 2023-04-03

AtCoder Regular Contest 159

A、1完。Bはかなり地道で確実な高速化が求められたが、時間内にやりきれなかった。無念。1完でも水パフォだったのでRatingは横ばいだった。Bみたいな問題、ねばって解けるようになりたい。最近いつも言ってるが、Bが解ければ入水だった。

A - Copy and Paste Graph

おもしろい。しばらく考えていると、コピペした部分は気にしなくて良いとわかり、ワーシャルフロイドだけでいける。 2023-04-08

B - GCD Subtraction

解説に書いてあることはすべて気づいていたが、最後までTLEを解消できなかった。一番効いていたのはA-B=1になったら、あとは1ずつ引くだけなので+B回。以上。ということ。この処理を入れないと遅すぎて全く解けなかった。 2023-04-08

if A - B == 1:
    count += B
    break

AtCoder Beginner Contest 297

4完。もうちょっとで入水！って思ってからだいぶ経ったけどまだ無理。問題E、難しいしいい問題だった。80分残ってても解けず、完敗だ。今日もGまで事後AC。でもなんか報われないなぁ。今回勉強になるいいコンテストだなぁ。

E - Kth Takoyaki Set

これ、問題読むとめっちゃ典型っぽいのに、わからんかった。Ai円のものを何個でも買っていいとき、安い方からK番目の金額は？複数の商品を買って金額の合計を求めたり、いくら以下の組み合わせを求めたり、というのは経験してるけど、わからん。ダイクストラだと。確かに。これ解けたらかなりスカッとするだろうと思ったけど、結構解かれててすげぇとしか思わない。 2023-04-09

F - Minimum Bounding Box 2

ぼくは基本順番にしか解かないのでコンテスト中やらなかったけど、これも非常に勉強になるいい問題。長方形の面積の期待値を求めたい。これを、(i,j)が長方形に含まれる確率の合計と、「主客転倒」させて解く。いやー「主客転倒」かっけー。こういうの時間内に解きたい！ 2023-04-09

G - Constrained Nim 2

読んですぐGrundy数とわかるが、石の数が10^9と書いてあり、ループ回して計算できない。実験するといいよ、と解説に書いてあったので実験してみると、規則性が一目瞭然だった。そういうテクニック、身につけねば。規則を前提とすれば、超短いコードでAC！ふぅ。解きてぇなぁ。お、100msで現在実行時間2位！ 2023-04-09

N, L, R = map(int, input().split())
xor = 0
for a in map(int, input().split()):
    xor ^= a % (L+R) // L
if xor:
    print('First')
else:
    print('Second')

過去問チャレンジ

ABCでなんとか4問解けるようになりたいので、D、Eあたりの過去問をランダムにピックアップして練習してみようと思いました。昔のABCを見ると問題数も難易度も全然違うため、101以降のコンテストにし、問題はやってみて選ぶことにしました。

ABC119 D - Lazy Faith

ABC266で初めて参加したので知りませんでしたが、このときは8問じゃなかったんですね。ABC119は問題Dまでしかありません。難易度もどんな設定なのか？最後の問題だからむずかしいのか？なぞですが、1~2時間くらいで自力で解けました。ABC266とABC267の最終問題Exがむずかしすぎたので解けたのが意外でうれしいです！プレ処理でデータを作り変えておいて、結果を出力するところはあまりがんばらなくても良いようにするパターンだなぁと徐々に思って、最初に走査してxの両側の一番近いsとtを見れば良いと、ひらめくことができました。sとtの最初と最後に-INFと+INFを入れるだけでコードがスッキリしてミスも減るので、あとで修正しました。

Submission #34662313 - AtCoder Beginner Contest 119

bisectという2分探索して挿入か所のidを返してくれるライブラリを使っている人がいたので、使ってみます。まさにその情報が欲しいので、そんな機能があったとは便利すぎます。最初からこう書けるようになりたいものですが、ぼくが書いた最初のコードに比べて、このコードは自分で何もしてなさすぎますね。bisect使うから前処理を何もせずにいきなり解けてしまっていいいのでしょうか？そう考えると最初に書いたコードの方が好きです。この2つのコードを比べると最初のほうが速いです。 2022-09-07

import bisect
a, b, q = map(int, input().split())
s = [int(input()) for _ in range(a)]
t = [int(input()) for _ in range(b)]
s = [-10**11] + s + [10**11]
t = [-10**11] + t + [10**11]
for _ in range(q):
    x = int(input())
    i = bisect.bisect(s, x)
    j = bisect.bisect(t, x)
    c,d,e,f = (x-s[i-1],x-t[j-1],s[i]-x,t[j]-x)
    res = min(max(c,d), max(e,f), 2*c+f, c+2*f, 2*e+d, e+2*d)
    print(res)

ABC183 E - Queen on Grid

現在のマスにたどり着く組み合わせの数は、現在のマスの左と左上と上方向にあるすべてのマスにたどり着く組み合わせの数の合計になるとわかります。2000x2000マスでこれをやると時間がかかりすぎるので、計算を減らす方法を考えると、同じ合計を何度も計算していることがわかり、それらを毎回計算せずに覚えておくことで計算量をO(HW)に減らすことができます。

h, w = map(int, input().split())
cells = [input() for _ in range(h)]
m = 1000000007
dp = [[[0]*4 for __ in range(w)] for _ in range(h)]
dp[0][0][3] = 1
for i in range(1,h):
    if cells[i][0] == '#':
        break
    dp[i][0][2] = (dp[i-1][0][2] + dp[i-1][0][3]) % m
    dp[i][0][3] = (dp[i-1][0][2] + dp[i-1][0][3]) % m
for j in range(1,w):
    if cells[0][j] == '#':
        break
    dp[0][j][0] = (dp[0][j-1][0] + dp[0][j-1][3]) % m
    dp[0][j][3] = (dp[0][j-1][0] + dp[0][j-1][3]) % m
for i in range(1,h):
    for j in range(1,w):
        if cells[i][j] == '#':
            continue
        dp[i][j][0] = (dp[i][j-1][0] + dp[i][j-1][3]) % m
        dp[i][j][1] = (dp[i-1][j-1][1] + dp[i-1][j-1][3]) % m
        dp[i][j][2] = (dp[i-1][j][2] + dp[i-1][j][3]) % m
        dp[i][j][3] = sum([dp[i][j][dir] for dir in range(3)]) % m
print(dp[h-1][w-1][3])

最初多重リストをこのように作ると、同じオブジェクトになってしまうというミスをしていました。

>>> l = [[0,0,0]]*4
>>> l
[[0, 0, 0], [0, 0, 0], [0, 0, 0], [0, 0, 0]]
>>> l[1][0] = 3
>>> l
[[3, 0, 0], [3, 0, 0], [3, 0, 0], [3, 0, 0]]

ぼくの環境でこのコードだと、2000x2000のマスが全部'.'だった場合、2秒以内に終わりませんでした。また、最初1000000007で割らずに実行していたらさらに時間がかかり、2000桁以上の数字が出力されました。1000000007で割る問題を初めてやりましたが、割らないとやってられないので納得です。 2022-09-07

割らない場合、noteの文字数制限のため、消した。 2023-03-05

ABC264 D - "redocta".swap(i,i+1)

隣同士の置換でatcoderにする最小回数。aを1番左に持ってきて、tを2番目に持ってきて…という処理を順番にやるのが最小回数であると考えて解きました。理由は、aを動かす時、aを除いた他の文字の並び順に影響しないからです。影響しないのであれば、aを最初に左に持ってこればいいし、それ以降の文字もすべて同じです。 2022-09-08

s = input()
atcoder = 'atcoder'
res = 0
for c in atcoder:
    i = s.find(c)
    res += i
    s = s.replace(c, '')
print(res)

ABC138 E - Strings of Impurity

前処理で文字列sを構造化することで、効率よく次の文字にジャンプしていきます。ABC119 D - Lazy Faithで覚えたばかりのbisectを使って解けました。難易度がよくわからないですが、どんどん自力で解けています。慣れてきたのでしょうか？ 2022-09-08

import sys
import bisect
s = input()
t = input()
s_data = {}
for i, c in enumerate(s):
    if c not in s_data:
        s_data[c] = [0, []]
    s_data[c][0] += 1
    s_data[c][1].append(i)
s_len = i + 1
watch = 0
repeat = 0
for c in t:
    if c not in s_data:
        print(-1)
        sys.exit()
    idx_in_c = bisect.bisect_left(s_data[c][1], watch)
    if idx_in_c == s_data[c][0]:
        repeat += 1
        watch = s_data[c][1][0] + 1
    else:
        watch = s_data[c][1][idx_in_c] + 1
print(s_len * repeat + watch)

ABC132 E - Hopscotch Addict

初めて参加したABC266 Fが「なもりグラフ」の問題で、グラフの問題は特殊な性質を使って解くのかなーと刷り込まれたと思います。と思ったら次に出会ったグラフの問題ABC267 Eはそんなこともなく、グラフだからといってむずかしく考えないのも大事と学びました。この問題、辺をたどって探索してたらどんどん枝分かれして計算量が増えすぎて解けないと思い、グラフのなんらかの特徴を捉えて構造化する方法がないか考えていましたが思いつかず、あきらめて解説を見ました。すると幅優先探索（Breadth First Search、BFS）で解くと書いてありました。あれ？普通にBFSかよ、なんだーというのが最初の感想ですが、それでいいことに気づくのが大事でした。ぼくは計算量が大きすぎると思っていましたが、よく考えたら最短経路を調べるときに同じ頂点を2回通る意味はないので、幅優先探索する計算量はO(N)なんですね。重要です。この問題はけんけんぱの3歩目で到達するか調べるということで、同じ頂点にmod(3)で同じ歩数で2回通る意味がない、という考え方をする必要があり、通常の最短経路の問題よりちょっと複雑です。計算量が3Nにはなってしまいますが、3Nは小さいです。queueにはdequeを使いました。 2022-09-08

import sys
from collections import defaultdict
from collections import deque
n, m = map(int, input().split())
nexts = defaultdict(list)
for _ in range(m):
    u, v = map(int, input().split())
    nexts[u].append(v)
s, t = map(int, input().split())
q = deque([])
come = [[0]*3 for _ in range(n+1)]
q.append((s, 0))
while q:
    cur = q.popleft()
    if cur[0] == t and cur[1] % 3 == 0:
        print(int(cur[1]/3))
        sys.exit()
    if not come[cur[0]][cur[1] % 3]:
        come[cur[0]][cur[1] % 3] = 1
    else:
        continue
    for next in nexts[cur[0]]:
        q.append((next, cur[1]+1))
print(-1)

ABC202 E - Count Descendants

時間がないのでしばらくやらないつもりだったのに、つい問題を見てしまいました。答えがわからないと気になってしかたありません。グラフの問題はこれまで3つ見て、自力で解けたことがありません。今回の問題は内容がシンプルで、今度こそ解けるかと思いましたが、またもや計算量もしくは空間計算量を減らすことができず、あきらめました。公式解説を見ましたが、トリッキー過ぎてビビります。木構造だと葉っぱのほうに向かって枝が広がっていくのをイメージしますが、太い幹のほうで葉っぱを挟んでいく感覚です。クレイジーですよね。しかし（）の入れ子構造だと言われると、（）の入れ子は木構造というのをどこかで見たことがあるような気もするので、慣れてる人にとっては当たり前の感覚なんでしょう。これでグラフの問題4連敗ですが、内容がそれぞれ個性的で刺激があって楽しいです。公式解説のC++コードがDFSを再帰呼び出しで実装しているように見えますが、深くなっても大丈夫なんでしょうか？ぼくはdequeを使って実装しました。このようなコードをPythonで書くだけで勉強になっているように感じられます。内容を理解した！と思ってテキトーにコードを書き始めたら、変なデータ構造をあとから追加したりしてわけがわからなくなることが多いです。紙にデータ構造や処理の流れを書くと、やることが明確になってコードがスラスラ書けます。bisectをまた使いました。覚えてから3回目。これは有用ですね。前処理がO(N)、1つのクエリーに対する処理はO(log(N))になると思います。 2022-09-09

from collections import defaultdict
from collections import deque
import bisect
n = int(input())
vertices = [[0]*3 for _ in range(n+1)] # [depth, in, out]
depth_out = defaultdict(list)
childlen = defaultdict(list)
for i, p in enumerate(map(int, input().split())):
    childlen[p].append(i+2)
s = deque([])
vertices[1][0] = 0
s.append(1)
time = 0
while s:
    time += 1
    p = s.pop()
    if not vertices[p][1]:
        vertices[p][1] = time
        depth = vertices[p][0]
        s.append(p)
        for child in childlen[p]:
            vertices[child][0] = depth + 1
            s.append(child)
    else:
        vertices[p][2] = time
        depth_out[vertices[p][0]].append(time)
q = int(input())
for _ in range(q):
    u, d = map(int, input().split())
    idx_in = bisect.bisect(depth_out[d], vertices[u][1])
    idx_out = bisect.bisect(depth_out[d], vertices[u][2])
    print(idx_out - idx_in)

EDPC T - Permutation

ABC282 Gの解説に、まずこの問題を考えてからやるとよい、と書いてあったため、やりましたが、トリッキー過ぎて理解するのに苦労しました。これはすごいですよね。解説のDPの説明はこうです。

dp[i][j]=(i番目までの位置関係を決めた時のi番目に決めた値がj番目に小さい数としたときの場合の数)

https://atcoder.jp/contests/dp/editorial/3722

意味不明な気がするのですが、みんなこれでわかるんですかね。わからないけど読み進めるかぁ、とボールの例を見ても意味不明で、最後に「なお、ボールの置き方の5通りそれぞれに対応する順列は次のようになります。」と書いてあります。全く意味不明のまま、ランニングしながら考えているうちに、わかりました。ボールの数字って並べ替えたあとのインデックスなんですね。つまり、並べ替えたあとの数字を[1][2][3]…と前から順番に決めていってることは確かなのですが、気持ち悪いことに、Nまで挿入しないと実際にどの数字が[1]なのか確定しません。挿入した時点でわかっていることは、もとの昇順の数列(1,2,3,4..,N)のなかでの、前後関係だけです。しかしこの操作で、i番目の数字を別の場所に挿入した順序同士が最終的にかぶることはないため、この操作を続けることで、場合の数を正しく数えることができます。これを解いたあとでもABC282 Gが同じと言われてもピンとこず、ABC282 Gも理解したころに、やっとこの考え方が身についてきたかな？というような状況です。ちなみに、ぼくの提出したコードの実行時間は84msで、Pythonでの提出の中で、現時点で最速でした！うれしい。その後、ABC282 GもACしましたが、現時点でPythonで2番手の実行時間です。 2022-12-18

M = 10**9+7
N = int(input())
s = input()
dp = [0,1]
for i, c in enumerate(s):
    i += 1
    dp_new = [0]*(i+2)
    if c == '<':
        memo = 0
        for j in range(1, i+1):
            memo += dp[j]
            dp_new[j+1] = memo
            dp_new[j+1] %= M
    else: # c == '>'
        memo = 0
        for j in range(i, 0, -1):
            memo += dp[j]
            dp_new[j] = memo
            dp_new[j] %= M
    dp = dp_new
print(sum(dp)%M)

ARC013 C - 笑いをとれるかな？

2023年初。現在去年の復習中。ABC278 Gを見直していて、Grundy数の問題1回しかやってなくて、次出てきた時反応できる気がしねぇと思い、ネットで検索してGrundy数の問題とされていたこの問題にたどり着きました。解く前からGrundy数の問題という先入観があり、問題を読むと豆腐を切っていく操作が行われているので、盤面が分岐していくパターンかなぁ？と思ったんですが、切ったら片方を食べるルールなので、分岐しません。で、豆腐の全側面にハバネロがある場合、どう切っても両方にハバネロが含まれてしまうので、負けの盤面です。ということはハバネロのAABBを切断したら負けで、そこに触れてはいけないことがわかります。ハバネロのAABBをGrundy数0とし、どうやってその外側を計算するかなぁと考え始めて気づいたのは、AABBの6つの側面の外側の厚みを石の数としたNimじゃんってことです。なので、周囲の厚みを全部計算してXORした値が0でなければ、先行が勝てます。問題文の書き方でNimがこうなってしまうことはとてもおもしろいですが、Grundy数の復習にはなりませんでした！とはいえ、実装せずとも思考の過程でGrundy数のことを考えられたので、それだけで復習になっているかもしれません。ところでこの問題、PyPyでやるとMLEになりました。問題を見るとメモリ制限: 64 MB。なんでやねん。厳しすぎる。昔はこんなに厳しかったんでしょうか？実際ACしてる人の多くはPyPyではなくPythonを使っています。なんでPyPyだとメモリ使用量が増えるのかもなぞですが、制限厳しすぎるしまあいいや。 2023-01-05

import sys
input = sys.stdin.readline
N = int(input())
xorall = 0
for _ in range(N):
    X, Y, Z = map(int, input().split())
    xmin = X
    xmax = 0
    ymin = Y
    ymax = 0
    zmin = Z
    zmax = 0
    M = int(input())
    for _ in range(M):
        x, y, z = map(int, input().split())
        xmin = min(x, xmin)
        xmax = max(x+1, xmax)
        ymin = min(y, ymin)
        ymax = max(y+1, ymax)
        zmin = min(z, zmin)
        zmax = max(z+1, zmax)
    xorall ^= xmin ^ ymin ^ zmin ^ X - xmax ^ Y - ymax ^ Z - zmax
if xorall:
    print('WIN')
else:
    print('LOSE')

APG4b EX24 - 時計の実装

使用言語をPythonからC++に変更したく、APG4bを始めています。非常に勉強になります。構造体の勉強で、時計の実装をする問題ですが、構造体自体には関係ないのですが、shiftという与えられた秒ずらす関数を実装せよという部分の繰り上げ、繰り下げ処理がちょっと難しいです。これでいいのか。  2023-02-01

    void shift(int diff_second) {
        int diff_hour = diff_second / 3600;
        diff_second %= 3600;
        int diff_minute = diff_second / 60;
        diff_second %= 60;
        second += diff_second;
        if (second >= 60) {
            second -= 60;
            minute += 1;
        }
        else if (second < 0) {
            second += 60;
            minute -= 1;
        }
        minute += diff_minute;
        if (minute >= 60) {
            minute -= 60;
            hour += 1;
        }
        else if (minute < 0) {
            minute += 60;
            hour -= 1;
        }
        hour += diff_hour;
        if (hour >= 24) {
            hour -= 24;
        }
        else if (hour < 0) {
            hour += 24;
        }
    }

蟻本ログ

プログラミングコンテストチャレンジブック [第2版]　～問題解決のアルゴリズム活用力とコーディングテクニックを鍛える～

知らないアルゴリズムが出てきて、解説を読んでもわからない時、そのアルゴリズムが蟻本に載っていたら読むことが多いです。ネットから離れて紙の本を読むって大事な時間です。これまで読んできた感想として、この本は、なんでも懇切丁寧にわかるように解説されているわけではないと感じています。すんなり理解できないことがしれっと書かれていたりして、そのたびに長考が必要です。でも、理解を深めるためには、それがいい。知らない手法に出会うたびに、関連する箇所を読んで、いずれ隙間なく読み終わりたいです。考察はABCの問題の方に書くことが多いので、ここに蟻本を読んだログをすべて書くわけではありませんが、気になったことがあれば書いていきたいです。 2022-11-22

3-2 厳選！頻出テクニック（1）

しゃくとり法。2問載っていますが、これはなんとかなりました。 2022-11-30

反転。Face The Right Wayという問題。これは難しく、何日も考えて問題を整理できましたが、どうしてもO(N^3)から計算量を減らせず、解けませんでした。機械をスライドさせながら操作するイメージですが、Kを固定して左から順番に回転させていくと、毎回K頭の牛の向きを更新しなければならず、O(N^2)の計算量から逃れられなかったのです。[i]から始まる牛を回転させるかどうか決めるときに影響を受けるのは、[i-K+1]から[i-1]までで回転させた回数です。なのでこの範囲の回転数の合計をsumとすると、1つ右の[i+1]に影響する回転数はsum-[i-K+1]+[i-1]というように、影響を受けない回転を引いて、新しく影響する回転を足す、という処理を逐次行うことでsumの計算（すなわち牛の回転）はO(N)でできることになります。これ、大事なセンスですね。ここがこの問題の肝でした。が、そこにたどりつくまでも結構むずかしいですね。Kを固定したときの操作順はなぜこれでいいのか？この操作ですが、順序によらず、どこで使うかの集合で結果が決まります。奇数回回転させると逆向きになるだけだからです。なので、一番左から操作していけば良いことがわかります。では一番左とはどこでしょうか？それは後ろを向いている最初の牛です。なぜなら、それより左の前を向いた牛に対して操作をすると、もとに戻すためにより左で操作する必要があるからです。これは一番左の操作から始めるという宣言に矛盾します。書いてて不思議なロジックだなとは思いますが。なので結局、Kを固定した場合、後ろを向いている牛に出会うたびに操作をしながら右に進んでいけばよいということになるのです。K=1は必ずすべての牛を前向きにできますので、答えが存在しないということはありません。可能性のあるすべてのKに対して調べて正解を出力します。ジャッジできませんが、Pythonで書いてみました。本に載っている例題は正解できました。sumは偶奇性だけが必要なので、1とXORで良いですね。 2022-12-03

N = int(input())
fb = [1 if c == 'F' else 0 for c in input()]
mincount = N+1
for k in range(1,N+1):
    count = 0
    flip = [0]*(N-k+1)
    sum = 0
    for i in range(N-k+1):
        if fb[i] == sum:
            count += 1
            flip[i] = 1
            sum ^= 1
        if i-k+1 >= 0:
            sum ^= flip[i-k+1]
    for i in range(N-k+1,N):
        if fb[i] == sum:
            # failed
            break
        if i-k+1 >= 0:
            sum ^= flip[i-k+1]
    else: # succeeded
        if count < mincount:
            mincount = count
            k_ans = k
print('K =', k_ans)
print('M =', mincount)

4-2 ゲームの必勝法を編み出せ！

ABC278 Gがゲームの問題で、解説によくわからない用語が出てきたので、読んでいます。コインのゲーム1 → これまでの経験の結果、自力でDPで解けました。A Funny Game (POJ 2484) → これがABC278 Gでも紹介されてた必勝法で、自分ではわかりませんでした。トリッキー過ぎてビビりますね。Euclid's Game → こういう数字を操作する話が出てくると、めんどくさいなぁとストレスに感じてしまいまいますが、なんとか我慢して（急にどんな話だったか思い出せない）ユークリッドの互除法を紙に書いて思い出し、眺めていると、ふと問題の構造がハッキリ見えて、自力で解けました。ぼくには、これを頭の中だけで見通すことはできないので、頭だけではなく、手も動かすことで正解に近づくことができます。 2022-11-22

Nim → 石の個数のXORを取る。XORが0のとき、石を取ると必ず0でなくなります。石を取るとその山の石の個数が減って変わるので、その山の個数のビットが変わります。どこかのビットが反転するとXORのビットは反転するので、必ず0でなくなります。XORが0でない時、0になるように石を取ることができます。XORの最上位ビットが1の山がある（XORが1なら1になっているオペランドが必ずあります。）ので、その山の石の個数を結果のXORが逆になる個数に減らせばよいです。オペランドのビットを反転させると、XORの同じビットも反転するので、そのように石を減らせばよいです。よって、XORが0でない状態で自分の番なら勝つことができる。最初、これも真似っこ戦略？と考え始めたけど、1山、2山ときて、3山の中に同じ個数の2山がある時、まではいけたけど、3山で石の個数が全部異なるパターンでわけがわからなくなりました。すべての山の石の数のXORという状態を使うなんて信じられないです。Georgia and Bob → 駒の間のマスの数を石の数と考え、右隣に好きな数移動して全部空にする問題と考えるとNimっぽく見えるなぁとは思いますが、これは無理ですね。発想がクレイジー過ぎます。右端の山から偶数番目の山だけに注目してNim。相手が奇数番目の山から移動して増やされた時は同じだけ取り除けば状態を維持できると。これは、、、これは無理だ。全く自分で思いつける気がしない。コインのゲーム2 → ここで出てくるGrundy数が目当てで、この章を読んでいたのですが、不思議な数字ですね。1手打ったときに移行できるGrundy数に含まれない最小の非負整数Mex（Minimum Excluded）がGrundy数であるとすると、Grundy数gからg-1以下のすべての状態に移行できるので、Grundy数を石の数と思えばNimに帰着できる。Grundy数は増やすこともできますが、相手に増やされた時は元の数字に減らして状態を維持することができます。わかりきってないような。 2022-11-23

Cutting Game → この問題の解説がなかなか理解できず、喫茶店で3時間考えて閉店になり、そのまま家でも考え続けていたら、寝る少し前くらいにようやく「あ～わかったかも」という気分になってきました。翌朝目が覚めたときにはある程度の理解が確信に変わりました。コインのゲーム2ででてきたGrundy数を使います。紙をこれ以上切れない状態がGrundy数0であり、自分の手のあとはすべての紙がGrundy数0である状態をキープすれば勝てるということがわかります。問題はコインのゲームのコインの山と違って紙がどんどん増えていくことです。紙を切って紙が増えたあとのGrundy数はどのように計算できるのか？蟻本には「2枚の紙がある状態のGrundy数というものを、g1 XOR g2として1つの数値で表すことができます。」と書かれています。これが説明なしにしれっと書かれているのが、なかなか理解できなかった原因でした。Nimではすべての山のXORをとり、それが0になるようにキープすることしか書かれていませんでした。が、実はこのXOR、Grundy数の性質を持っていることがわかります。まず、XORは1つのオペランドを変更する（石を取る）と、必ず変化します。つまり同じ状態には推移しません。これはGrundy数の性質です。XORの最上位ビットと同じ桁が1であるオペランドが必ず存在します。存在しなければXORのそのビットは0であるはずだからです。このオペランドを適当に変更するだけで、XORはそれ未満のすべての値に推移可能であることがわかります。XORは1つのオペランドのビットを反転すると、XORの同じ桁のビットが反転するため、XOR未満のすべての数字に推移可能です。これでXORはGrundy数の2つの性質を満たすことがわかりました。つまり、Nimにおけるすべての山の石の数のXORは、実はGrundy数だったのです。これ、蟻本に明示的に書かれていないですよね。そのため、なんでこれでいいの？と疑問に思い、考えまくることになったわけですが、これが蟻本のいいところですね。ゲームの盤面が2つに分裂した時、2つのGrundy数のXORを全体のGrundy数とすることができます。これで初期状態hwのサイズの紙のGrundy数を計算することができ、問題を解くことができます。NimでXORが出てきた時は、突拍子もなさすぎましたが、一通り理解してみると、オペランドの変化に対してセンシティブであることが、XORを使う理由と言えるかも知れません。この章で学んだゲーム必勝法を羅列すると、DP、真似っこ戦略、Nim、Grundy数です。真似っこ戦略は、Grundy数を覚えてから振り返ると、A XOR A=0ってことですね。しかしGrundy数、トリッキーでエグかった。Grundy数を理解できたので、ABC278 Gに戻ります。ABC278 Gも盤面が分裂していく基本的な構造をしていることがわかります。 2022-11-24

競プロ典型 90 問

自力で解けたらo、解けなかったらx。練習のためC++での回答必須、にしようと思ったけど、早く先に進みたくて慣れてるPythonでどんどんやりたくなってしまう。とはいえC++練習しないと。時間制限厳しいやつとか、気まぐれでC++でも回答しよう。ていうか90問やるとこのnoteの文字数が危ないな。

001 - Yokan Party（★4）

x 最初、サイズが小さい順に隣とくっつけていくんじゃないかと思ったが、その方針でどう実装すればよいかわからなかった。2分探索をちゃんとやったことがないので、典型として学べて良かった。ABC270 Eの解説を見たときも驚いたのを思い出す。 2023-02-08

N, L = map(int, input().split())
K = int(input())
cuts = list(map(int, input().split())) + [L] # last idx=N
l = 0 # ge l is possible
r = L # ge r is impossible
while l + 1 < r:
    score = (l + r) // 2
    start = 0
    count = 0
    for i in range(N+1):
        if cuts[i] - start >= score:
            start = cuts[i]
            count += 1
    if count > K:
        l = score
    else:
        r = score
print(l)

002 - Encyclopedia of Parentheses（★3）

o なんとか解けた。最初のカッコの中にいくつカッコを入れるか？でループを回す。カッコが全部でi個の場合、最初のカッコの中身は0個からi-1個までありうる。外側に、それぞれi-1個から0個までありうる。iが小さい順に生成していくと、組み合わせで全部作れる。最初から辞書順生成できるかもしれないが、最後にソートして辞書順にした。 2023-02-08

import sys
N = int(input())
if N % 2 != 0:
    sys.exit()
N //= 2
ans = [[] for _ in range(N+1)]
ans[0].append('')
ans[1].append('()')
for i in range(2, N+1): # make ans[i]
    for j in range(i)[::-1]: # i-1 -> 0
        k = i-1-j
        for x in ans[j]:
            for y in ans[k]:
                ans[i].append(''.join(['(',x,')',y]))
for i in sorted(ans[N]):
    print(i)

003 - Longest Circular Road（★4）

o うほ、短時間で解けた。木の直径というやつだ。以前木の直径が必要なABC267 Fを、木の直径を知らずに自力で解いたことあり。 2023-02-08

004 - Cross Sum（★2）

o 内包表現使いまくりで短い。 2023-02-09

005 - Restricted Digits（★7）

まだ整理しきれず。mod BでB-1周期で繰り返すのと、途中で0になるのがある。繰り返しの理由もわからん。まあ、計算させてしまえばいいか…。がんばろ。 2023-02-09

x 上に書いたぼくの方針ですが、桁を上に追加していこうとしたせいで、沼にはまってました。上に追加すると、たとえば、3、30、300、と積み重ねていって、modがどこかでループするからぁ、みたいなことを考えてたんですが、桁を下に挿入すると確定分を10倍して1桁の数字を入れるだけなので、全部統一的に処理できますね。ていうか一度上に追加していこうと思ったときに、そのまま抜け出せないってのがすごい弱点のような気がします。解説見てそう思うことが結構あるような。っていうか解けない問題って誰でもそんなもんだったりするんですかね？畳み込みでさらに高速化できるみたいで、できれば練習しておきたいところです。 2023-02-14

M = 10**9 + 7
N, B, K = map(int, input().split())
clist = list(map(int, input().split()))
dp = [[0]*B for _ in range(60)]
for c in clist:
    dp[0][c%B] += 1
power = 10 % B
for i in range(1, 60):
    for j in range(B):
        for k in range(B):
            nj = (j * power + k) % B
            dp[i][nj] += dp[i-1][j] * dp[i-1][k]
            dp[i][nj] %= M
    power *= power
    power %= B
x = 0
ans = [0]*B
ans[0] = 1
power = 10 % B
init = False
while N:
    ans_next = [0]*B
    if N & 1:
        for j in range(B):
            for k in range(B):
                nj = (j * power + k) % B
                ans_next[nj] += ans[j] * dp[x][k]
                ans_next[nj] %= M
        ans = ans_next
    N >>= 1
    x += 1
    power *= power
    power %= B
print(ans[0])

006 - Smallest Subsequence（★5）

o 最初にaを使えるだけ使うなぁ、というところから考えて、次はb、次はcと順番に使えるだけ使えばよいと思ったら勘違い。2つ目のサンプルで引っかかった。1文字ずつ可能な限り小さい文字を選ぶ必要あり。 2023-02-09

import bisect
N, K = map(int, input().split())
ORDA = ord('a')
S = input()
chars = [[] for _ in range(26)]
for i, c in enumerate(S):
    chars[ord(c)-ORDA].append(i)

left = K # count of chars left
next = 0
ans = []
while left:
    for i in range(26):
        idx = bisect.bisect_left(chars[i], next)
        if idx < len(chars[i]) and chars[i][idx] <= N - left:
            ans.append(chr(ORDA+i))
            left -= 1
            next = chars[i][idx] + 1
            break
print(''.join(ans))

007 - CP Classes（★3）

o クラスのレーティングはsetでユニークにしてからソート、生徒のレーティングもソートするけど、回答するときは番号順に戻す必要があるので、レーティングと番号のtupleにしておく。小さい順に1つずつ進めて全部調べた。 2023-02-09

008 - AtCounter（★4）

o 2023-02-09

009 - Three Point Angle（★6）

o 学びあり。まず、偏角を求めることはわかったが、x軸方向の単位ベクトルとの内積を計算し、math.acosで[0,π]の角度を求め、y座標が負なら-をつける、みたいなことを最初やってた。math.atanなら内積みたいな大変な計算いらないじゃん。そればかりか、math.atan2(y,x)で4象限の角度に対応できるとは、これは大事な知恵を得た。また、最初2分探索で角度が一番大きい可能性のあるベクトルを探してたが、遅かった。2分探索ならO(N log(N))、しゃくとり法ならO(N)であるばかりか、2分探索の方が余計な条件文が増えてコードもわかりにくくなってしまった。最初しゃくとり法でできなかったのは、偏角の-πとπの間をどうすべきか気になっていたからだ。しかしそれは、円のイメージができていなかったからと言える。しゃくとり法に変更することで2秒以上かかってたのが700ms台に高速化した。 2023-02-10

import math
# EPSILON = 1e-7*math.pi/180.0
N = int(input())
P = [tuple(map(int, input().split())) for _ in range(N)]
rads = [[] for _ in range(N)]
for i in range(N):
    for j in range(i+1, N):
        rad = math.atan2(P[j][1] - P[i][1], P[j][0] - P[i][0])
        rev = rad + math.pi
        if rev > math.pi:
            rev = rad - math.pi
        rads[i].append(rad)
        rads[j].append(rev)
for i in range(N):
    rads[i].sort()
ans = 0.0
for i in range(N):
    radsi = rads[i]
    j = 0
    k = 1
    while k < N - 1:
        ang = radsi[j] + math.pi - radsi[k]
        if ang > 0:
            ans = max(ans, math.pi - ang)
            k += 1
        else:
            ans = max(ans, math.pi + ang)
            j += 1
print(math.degrees(ans))

010 - Score Sum Queries（★2）

o 区間和ということで、フェニック木とかも思い浮かぶが、ここは累積和で。練習問題っぽいのやったことないのでうれしい。ところでinput = sys.stdin.readlineをつけるだけで、処理時間が555msから161msとなり、実行時間で1ページ目に載った。大量に読み込む問題では差が顕著。 2023-02-10

011 - Gravy Jobs（★6）

x できず。やる仕事を固定した場合、締切が早い順にやれば良い、と言われると確かにそうとわかるのだが、だから締切が早い順に仕事をソートした上でDPという2ステップを、自力で踏んで正解にたどり着くことができない。難しい。 2023-02-15

N = int(input())
joblist = [tuple(map(int, input().split())) for _ in range(N)] # d,c,s
joblist.sort(key=lambda x:x[0])
dp = [0]*(joblist[-1][0]+1)
for d, c, s in joblist:
    for j in range(d-c+1)[::-1]:
        dp[j+c] = max(dp[j+c], dp[j] + s)
print(max(dp))

012 - Red Painting（★4）

o Union-Find。なんか他の人より遅くて気になる。 2023-02-15

013 - Passing（★5）

o ひらめいた！問題を読んで誰でも、ダイクストラ法の問題っぽいと思うだろうけど、特定の街を経由しろ、しかも全街に対して答えろとのことで、あれぇ？と悩んでしまう。しかしよく考えたら、ダイクストラ法って全街に対して最短経路が求まってるから、1とN、両側からダイクストラ法をやって、経由する街までのコストを足せばよい。解くことによって、ダイクストラ法について考える機会を与えてもらった。あと、エッジのコストが1のダイクストラ法しかいままでやったことなかったので、ライブラリを書き直す機会にもなってよかった。 2023-02-16

014 - We Used to Sing a Song Together（★3）

o ACしたけど、証明難しくて結構考えたし、実は証明しきれいていない。2人の小学生と2校の並びは、aabb、abab、abba、の3通りしか無い。この内、1つ目は学校をスワップしても不便さは変わらないが、2つ目、3つ目は不便になってしまう。小学生と学校をソートして左から順にペアリングしていくと、どの2人と2校を見ても不便じゃない方の並びになっている。ということまで考えたけども、証明になってなくない？ 2023-02-15

N = int(input())
alist = list(map(int, input().split()))
blist = list(map(int, input().split()))
alist.sort()
blist.sort()
ans = 0
for a, b in zip(alist, blist):
    ans += abs(a-b)
print(ans)

015 - Don't be too close（★6）

x できず。カウントする時点で、ぼくの頭にはDPしか選択肢がなく、どうやってDPに持ち込むか？しか考えてなかった。計算量をO(N^2)から改善できず行き詰まった。なんと、すべてのkに対して、chooseで組み合わせの数を計算するのが正解らしい。計算量が調和級数でO(N log(N))に収まるんだとか。となりのボールの差がk以上の場合、選べる個数はN/k個くらいなので、選べる個数でループすると、N/k回で終わる。よってkを1からNまで調べる計算量の合計はN log(N)！えげつないなぁ。DPじゃないんだなぁ。そもそも、組み合わせの数を求める式が、a個選択する場合、(N-(k-1)(a-1))Ca。これも出てこなかった。a-1個の隙間にk-1個のボールをキープしておいて、残りからa個選べばよいためだ。高校生の時なら思いついたかもなどと思えて、くやしい。 2023-02-16

M = 10**9 + 7
N = int(input())
fact = [0]*(N+1)
invfact = [0]*(N+1)
fact[0] = 1
for i in range(1, N+1):
    fact[i] = fact[i-1] * i % M
invfact[N] = pow(fact[N], M-2, M)
for i in range(N-1, 0, -1):
    invfact[i] = invfact[i+1] * (i+1) % M
invfact[0] = 1
def choose(n, r):
    return fact[n] * invfact[r] * invfact[n-r] % M
for k in range(1, N+1):
    ans = 0
    for a in range(1, N+1):
        keep = (k-1)*(a-1)
        if keep + a > N:
            break
        ans += choose(N-keep, a)
        ans %= M
    print(ans)

016 - Minimum Coins（★3）

x レベル3なのに解けず悲しい。1つ前の015といっしょで、なんかDPに持ち込めばOKみたいな考えから脱出できず、行き詰まるケースが多いと気付かされる。競プロ半年くらいでいろいろ身についたような気がするけど柔軟性を失った状態なんだ。 2023-02-16

N = int(input())
M = 10000
a, b, c = map(int, input().split())
ans = M
for i in range(M):
    sumi = a*i
    if sumi > N:
        break
    for j in range(M-i):
        sumj = sumi + b*j
        left = N - sumj
        if left < 0:
            break
        if left % c == 0:
            ans = min(ans, i + j + left//c)
print(ans)

017 - Crossing Segments（★7）

o レベル7だけど自力で解けた。やった！問題がすごくシンプルで、いかにも典型問題っぽいのに、最初全然解き方がわからなかったが、なんかふとひらめいた。なんでひらめいたのか？なぞだけれども。なんでひらめいたのかなぁ。あんなにしばらく検討つかなかったのに。まずLでソートし、Lが小さい順にRの位置に印をつけていく。現在見ているL、Rの間に印があれば、確かに交わっている。印のカウントはRange Sumが必要なので、フェニック木を使った。同じLの時にカウントしてはいけないので、Lは小さい順だが、Rは大きい順にソートしなければならないことに注意。017までACしてペナルティ0なのがちょっと気持ち悪い。 2023-02-16

018 - Statue of Chokudai（★3）

o 基本的な三角関数の問題だけど、ていねいにやらないとミスる。回転方向が最初-y方向だよとか、atan2の引数の順序とか。atan2の引数、覚えたとき(y,x)が自然だなぁと感じたけど最初ミスってた。大丈夫と思ってもそういうもん。 2023-02-18

019 - Pick Two（★6）

x 「区間DP」らしい。だいぶ考えたけど閃かず。疲れた。区間DPには、ABC273 Fで1度だけ出会ったことがあるが、複雑な実装が必要で疲れたの覚えてる。これは思いつかん。これが区間DPで解く問題なのか。区間DP、bitDP、挿入DP、桁DP、木DP。ひらめけ！ 2023-02-18

N = int(input())
alist = list(map(int, input().split()))
dp = [[10**9]*(2*N) for _ in range(2*N)] # L 0-(2N-2), R 1-(2N-1)
for l in range(2*N-1):
    dp[l][l+1] = abs(alist[l] - alist[l+1])
for w in range(3, 2*N, 2):
    for l in range(2*N-w):
        dp[l][l+w] = dp[l+1][l+w-1] + abs(alist[l] - alist[l+w])
        for l2 in range(l+2, l+w, 2):
            dp[l][l+w] = min(dp[l][l+w], dp[l][l2-1] + dp[l2][l+w])
print(dp[0][2*N-1])

020 - Log Inequality（★3）

o math.log2を使ってもサンプルはACするけど、整数で解かないと誤差でNGになりそうと勘が働いてミスらず解けた。しかし、b*log2(c)=log2(c^b)という変形、忘れてたので改めて導いた。こんなことすら、全然使ってないからちょっと立ち止まるのつらい。あと、実行速度見ると、PyPyではなく、Python使ってる人が数倍速いの納得いかん。なんだかんだ20問解いて、まだペナルティ0。どっかでミスったほうが気が楽なんだが。 2023-02-18

a, b, c = map(int, input().split())
if a < c**b:
    print('Yes')
else:
    print('No')

021 - Come Back in One Piece（★5）

o 強連結成分の条件そのものなので、いけた。ノーミス継続。 2023-02-18

Submission #38957535 - 競プロ典型 90 問

022 - Cubic Cake（★2）

o ユークリッド互除法の復習ができた。これもPyPyよりPythonが速いっぽい。 2023-02-18

def gcd(a, b):
    while b:
        a, b = b, a % b
    return a
A, B, C = map(int, input().split())
ab = gcd(A, B)
abc = gcd(ab, C)
print((A+B+C)//abc - 3)

023 - Avoid War（★7）

x かなり難しい。下と右に1行1列足して、2x2の領域を何個入れられるか？みたいな問題かな？（この考察ちょっと気に入ってるけど。）とか、あるいはグラフの問題かな？とか頭の中で考えてたけど、結局わからず、解説を見た。左上から順に調べていって、次のマスにキングを置けるかどうかに影響する部分（具体的には直前のW+1マス）の配置パターンごとにカウントしながらDPらしい。えげつないと思ったが、なんとか実装して提出も、ACx12、WAx12、TLEx1に沈んだ。サンプルケース4も通ってない。1、2、3、5は通ってるのに4だけ通らない。しかし結構サイズでかい。公開されているテストケースでサイズが小さいもので調べるか。ハードそうなので一旦退散。と思ったらバグ見つけてTLEx1まで来た。TLEのテストケースは24x24で全部'.'のケースだった。ちょっと頭が限界なのでまた退散。他のすごい人たちの回答を見ると、04_10.txtだけ答えをハードコードしてる人も多数。よほど厳しいテストケースなのだろう。ACも可能と思われるが、エネルギーを使うメリットが少なそうなので、ここはTLEx1のまま完了としておく。ちなみに自分のマシンのPythonでは40秒くらいで正解が出力された。たぶんAtCoderのサーバーでは、8秒の制限をちょっとオーバーするくらいなのだろう。 2023-02-19

import sys
from collections import defaultdict
from itertools import combinations
M = 10**9 + 7
H, W = map(int, input().split())
clist = []
for _ in range(H):
    clist.extend([c=='.' for c in input()])
pow2 = [1]*(W+1) # 2^0 ~ 2^W
for i in range(1, W+1):
    pow2[i] = pow2[i-1] * 2
pow2W = pow2[W]
# initialize
dp = defaultdict(int)
watch_next_line = (H >= 2 and clist[W])
for count in range((W+1)//2+1):
    for combi in combinations(range(W-count+1), count):
        bits = 0
        for i, sel in enumerate(combi):
            if not clist[i+sel]:
                break
            bits += pow2[i+sel]
        else: # if break it was impossible
            dp[bits] = 1
            if watch_next_line \
            and (not combi or (combi[0] != 0 and (W == 1 or combi[0] != 1))):
                dp[bits + pow2W] = 1
if H == 1:
    print(len(dp))
    sys.exit()
mask0 = 1
mask1 = 2
mask2 = 4
maskW = pow2W
mask0W = (mask0|maskW)
for i in range(W+1, H*W):
    dp_next = defaultdict(int)
    for bits, count in dp.items():
        next_bits = bits >> 1
        dp_next[next_bits] += count # don't select the new cell
        dp_next[next_bits] %= M
        if clist[i] and bits&mask1 == 0 \
        and (i%W == 0 or bits&mask0W == 0) and (i%W == W-1 or bits&mask2 == 0):
            next_bits += pow2W
            dp_next[next_bits] += count
            dp_next[next_bits] %= M
    dp = dp_next
ans = 0
for count in dp.values():
    ans += count
    ans %= M
print(ans)

024 - Select +／- One（★2）

o

Submission #39004801 - 競プロ典型 90 問

025 - Digit Product Equation（★7）

o レベル7だけどひらめいた！思考の流れとして、まずN以下の正数全探索いけるかな？と考え、10^11だから間に合わないな。と気づくステップを踏むべきなのだろう。そこから√Nになるのかな？とか検討できる。この問題に関しては、f(m)の値は数字の組み合わせだけで決まるので、全部調べなくて良いと気づけばいい。1~9の9個の数字10個の組み合わせは18C8通りで、計算してみると43758だった。この数字を見て、少ない！いける！とテンションが上がる。Bが0を含む場合は別扱いした。レベル7が自力で解けてうれしい。インデックスのコンビネーションから数字を復元する処理は、すぐ書けると今後うれしいかもしれない。解説には再帰関数でと書いてあるけどPythonでは無理だなぁ。 2023-02-25

from itertools import combinations
N, B = map(int, input().split())
keta_max = len(str(N))
ans = 0
for keta in range(1, keta_max+1):
    for splits in combinations(range(keta+8), 8):
        combi = [1]*splits[0] # combi is numbers used
        for i in range(1, 8):
            combi += [i+1]*(splits[i]-splits[i-1]-1)
        combi += [9]*(keta+7-splits[7])
        multi = 1
        for i in combi:
            multi *= i
        m = multi + B
        if m <= N:
            combi_ = []
            while m:
                combi_.append(m%10)
                m //= 10
            if combi == sorted(combi_):
                ans += 1
if B <= N: # check B include '0'
    b = B
    while b:
        if b%10 == 0:
            ans +=1
            break
        b //= 10
print(ans)

026 - Independent Set on a Tree（★4）

o 深さが偶数と奇数の頂点は隣り合わないし、どちらかのグループはN/2個以上頂点があるので、越えた分引けばいい、という方針で解いた。解説に2部グラフについて書いてある。直接結ばれた頂点同士が違う色になるように塗ることができるグラフを2部グラフという。奇数長の閉路を含まない。そして、木は必ず2部グラフである。 2023-02-25

N = int(input())
Nhalf = N // 2
G = [[] for _ in range(N+1)]
for _ in range(N-1):
    a, b = map(int, input().split())
    G[a].append(b)
    G[b].append(a)
depth = [-1]*(N+1)
depth[1] = 0
stack = [1]
while stack:
    cur = stack.pop()
    for next in G[cur]:
        if depth[next] == -1:
            depth[next] = depth[cur] + 1
            stack.append(next)
evens = []
odds = []
for v in range(1, N+1):
    if depth[v] % 2 == 0:
        evens.append(v)
    else:
        odds.append(v)

if len(evens) >= Nhalf:
    while len(evens) > Nhalf:
        evens.pop()
    print(*evens)
else:
    while len(odds) > Nhalf:
        odds.pop()
    print(*odds)

027 - Sign Up Requests （★2）

o

028 - Cluttered Paper（★4）

o いかにも典型の中の典型という典型問題で、1度やっておきたかったので出てきてうれしいし、難しかったし、恐る恐る2次元いもすも、自力ACできてうれしい。ふぅ。この問題は座標が1000以下に抑えられてるが、座圧したらでかい座標でもいけるはずで、そのような問題もやっておきたい。ただし計算量はO(N^2)なので、その場合、Nは数千が限界のはず。この問題の制約であるN=100000では、解けなくなる。 2023-02-25

N = int(input())
grid = [[0]*1001 for _ in range(1001)]
for _ in range(N):
    lx, ly, rx, ry = map(int, input().split())
    grid[lx][ly] += 1
    grid[rx][ly] -= 1
    grid[lx][ry] -= 1
    grid[rx][ry] += 1
for y in range(1000): # id 1000 is not needed
    cur = 0
    for x in range(1000):
        cur += grid[x][y]
        grid[x][y] = cur
for x in range(1000):
    cur = 0
    for y in range(1000):
        cur += grid[x][y]
        grid[x][y] = cur
ans = [0]*(N+1)
for x in range(1000):
    for y in range(1000):
        ans[grid[x][y]] += 1
print(*ans[1:], sep='\n')

029 - Long Bricks（★5）

x 初めての「遅延セグ木」。難しいがなんとかやりきった。👀に書いていたアルゴリズムなので、リストから消すことができた。「遅延セグ木」という名前はずいぶん前から耳に入って気になってたけど、後回しにしてた。なぜって理解するのが大変だから。土曜朝から考えてて、21時のARCの開始時間までに実装しきれなかった。こうして典型90に出てきて、無理にでも理解しなければならない状況になって、本当にありがたい。効率的なコードになってない懸念を感じながら実装したけど、現状Python勢の提出の中で、42ページ中7ページ目に出てくるのでまあまあの速度が出ているようだ。「遅延セグ木」だが、範囲を一気に更新しても高速に処理できる。今までのようにボトムアップでやっていると更新にO(N logN)かかってしまうところ、O(logN)でできるはず。更新範囲は、queryの処理と同じように必要なノードを取り出して、それより上だけを更新し、その下の末端までは値を更新しない。代わりにlazyという値を持っておき、この値を持っているノードの子は更新されていないという印にする。そして別の更新やクエリの処理のために、それより下のノードの値が必要になったときに、初めて子のノードに伝搬させる。伝搬が済んだらlazyはNoneにしておく。伝搬するときに確認するノード一覧をupper_nodesという関数で取得できるようにし、それで取れるインデックスを、伝搬や、上に向かっての更新処理に使用する。 2023-02-26

class SEGT_LAZY():
    INF = 10**10
    DEFAULT = 0 # need update
    def __init__(self, n):
        '''input n is maxid+1, this is 0 start'''
        self.n = 1
        while self.n < n:
            self.n *= 2
        self.maxima = [self.DEFAULT]*(2*self.n)
        self.lazy = [None]*(2*self.n) # None?
    def upper_nodes(self, l, r):
        '''return indices are bottom to top'''
        res = []
        l += self.n - 1
        r += self.n - 1
        lget = (l%2 == 0)
        rget = (r%2 == 0)
        while l > 0:
            l = (l-1) // 2
            if lget:
                res.append(l)
            else:
                lget = (l%2 == 0)
            r = (r-1) // 2
            if rget and (not res or res[-1] != r):
                res.append(r)
            else:
                rget = (r%2 == 0)
        return res
    def propagate(self, upper_nodes):
        '''upper_nodes must be top down'''
        '''so reverse of self.upper_nodes'''
        for idx in upper_nodes:
            if self.lazy[idx] is None:
                continue
            self.lazy[2*idx+1] = self.lazy[2*idx+2] \
                = self.maxima[2*idx+1] = self.maxima[2*idx+2] \
                = self.lazy[idx]
            self.lazy[idx] = None
    def range_update(self, l, r, a):
        '''force overwrite [l,r) with a'''
        upper_nodes = self.upper_nodes(l, r)
        self.propagate(reversed(upper_nodes))
        l += self.n - 1
        r += self.n - 1
        while l < r:
            # always update currently
            if l & 1 == 0:
                self.lazy[l] = self.maxima[l] = a
                l += 1
            if r & 1 == 0:
                r -= 1
                self.lazy[r] = self.maxima[r] = a
            l >>= 1
            r >>= 1
        for idx in upper_nodes:
            self.maxima[idx] \
                = max(self.maxima[2*idx+1], self.maxima[2*idx+2])
    def query(self, l, r):
        self.propagate(reversed(self.upper_nodes(l, r)))
        resL = resR = self.DEFAULT
        l += self.n - 1
        r += self.n - 1
        while l < r:
            if l & 1 == 0:
                resL = max(resL, self.maxima[l])
                l += 1
            if r & 1 == 0:
                r -= 1
                resR = max(resR, self.maxima[r])
            l >>= 1
            r >>= 1
        return max(resL, resR)

W, N = map(int, input().split())
segt = SEGT_LAZY(W+1)
ans = []
for _ in range(N):
    L, R = map(int, input().split())
    highest = segt.query(L, R+1)
    segt.range_update(L, R+1, highest+1)
    ans.append(highest+1)
print(*ans, sep='\n')

030 - K Factors（★5）

o 結構長考したけど、ひらめいた！エラトステネスの篩の応用じゃん。長考した原因は10000000までやって間に合うとなかなか気づかなかったためだけど、よく考えたら2の倍数は1/2個、3の倍数は1/3個、と調和級数の和になるから、O(N logN)に抑えられると気づいた！おもしろい。エラトステネスは紀元前275-194年の人。ユークリッドの互除法が最古のアルゴリズムと思ってたけど、割と近い。どちらもすごいアルゴリズムで感動する。解説によると、調和級数を素数に限定すると計算量はさらに少なく、O(N log logN)になるらしい。 2023-02-26

031 - VS AtCoder（★6）

o Grundy数は一応勉強してたので、自力でいけた。しかし、実は、計算量多くて間に合わんだろと思って解説見て、間に合うと書いてあったのを見てからやったという事情あり。Grundy数の計算はWが50まで、Bが50+51x25=1325までのループで、その中で遷移先がBの半分なので、平均330くらいとしてかけると、せいぜい2200万くらいか…。たしかにこれなら許容範囲。しかしO(W B^4)って考えると50^5=3億1250万。無理って思っちゃわない？これいけるって判断するのなかなか難しいな。冷静に見積もりたいところ。 2023-02-28

grundy = [[] for _ in range(51)] # W 0-50 B 0-1325
grundy[0].extend([0, 0])
for b in range(2, 1326):
    cango = set()
    for k in range(1, b//2 + 1):
        cango.add(grundy[0][b-k])
    mex = 0
    while mex in cango:
        mex += 1
    grundy[0].append(mex)
for w in range(1, 51):
    for b in range(1326):
        cango = set()
        if b+w < 1326:
            cango.add(grundy[w-1][b+w])
        for k in range(1, b//2 + 1):
            cango.add(grundy[w][b-k])
        mex = 0
        while mex in cango:
            mex += 1
        grundy[w].append(mex)
N = int(input())
xorall = 0
for w, b in zip(map(int, input().split()), map(int, input().split())):
    xorall ^= grundy[w][b]
if xorall == 0:
    print('Second')
else:
    print('First')

032 - AtCoder Ekiden（★3）

o 10!=3628800。これなら全探索いける。 2023-02-28

033 - Not Too Bright（★2）

o 不適切な条件が、「イルミネーション全体に完全に含まれる縦2×横2の、4 つのLEDを含む領域であって、点灯しているLEDが領域内に2つ以上あるものが存在する。」なので、縦か横が1なら2x2が含まれないので全部点いててOK。WAしてから考えて修正した。すごいひっかけだけど典型問題として入れてるのは、本当に気が利いてる。 2023-02-28

034 - There are few types of elements（★4）

o しゃくとり法。できる。できるんだが、スッとすばやく書ける感じではないことが反省ポイント。どんどんeを進めますよ、K種類超えたらsを進めてK種類以下にしますよ、というのをまず書いてしまう。最後に確定タイミングで毎回長さを評価する。ってことでまあ慣れればもっと速く書けるかなぁ？ 2023-02-28

035 - Preserve Connectivity（★7）

x 解説の1ページ目に「木DPをしよう」とでかでかと書いてあって、まじかよとギョッとしたけど、ぼくの中の「木DP」はABC287 Fなので、イメージと違う。この問題は普通の木の問題に見える。K頂点のLCA（Lowest Common Ancestor）を求める問題？と思って考えてたんだけど、K頂点のLCAって実は行きがけ順で最初と最後の2頂点のLCAなのでは？って気づいておもしろかった。でもこの問題はそのような問題でもない。この問題ではDFS行きがけ順の頂点順序が重要となっている。絵を描いていると、行きと帰り両方大事に見えるので、帰りがけ順かな？と思ったけど、どっちでもいいっぽい。なのでとりあえず行きがけ順に頂点を並べて、隣同士のLCAを求めて経路距離を求め、2重カウントしているので、合計を2で割ったのが答え。かなり難しい問題だった。 2023-03-01

import math
N = int(input())
G = [[] for _ in range(N+1)] # 1-N
for _ in range(N-1):
    a, b = map(int, input().split())
    G[a].append(b)
    G[b].append(a)

max_double = math.floor(math.log2(N-1))
preorder = [-1]*(N+1)
count = 0
depth = [-1]*(N+1)
parents = [[-1]*(N+1) for _ in range(max_double + 1)]
root = 1
stack = [(root, 0)]
while stack:
    cur, dist = stack.pop()
    depth[cur] = dist
    preorder[cur] = count
    count += 1
    for next in G[cur]:
        if depth[next] != -1:
            continue
        parents[0][next] = cur
        x = 0
        while x < max_double:
            if parents[x][parents[x][next]] == -1:
                break
            parents[x+1][next] = parents[x][parents[x][next]]
            x += 1
        stack.append((next, dist+1))

def climb(p, step):
    x = 0
    while step:
        if step&1:
            p = parents[x][p]
        step //= 2
        x += 1
    return p

Q = int(input())
for _ in range(Q):
    k, *vs = map(int, input().split())
    vs.sort(key=lambda x:preorder[x])
    vs.append(vs[0])
    ans = 0
    for i in range(k):
        p1 = vs[i]
        p2 = vs[i+1]
        if depth[p1] < depth[p2]:
            p2 = climb(p2, depth[p2] - depth[p1])
        elif depth[p1] > depth[p2]:
            p1 = climb(p1, depth[p1] - depth[p2])
        if p1 == p2:
            lca = p1
        else:
            for x in range(max_double+1)[::-1]:
                if parents[x][p1] != -1 and parents[x][p1] != parents[x][p2]:
                    p1, p2 = parents[x][p1], parents[x][p2]
            lca = parents[0][p1]
        ans += depth[vs[i]] + depth[vs[i+1]] - 2*depth[lca]
    ans //= 2
    print(ans)

036 - Max Manhattan Distance（★5）

o 45度回転すると、マンハッタン距離が、チェビシェフ距離になって簡単に計算できるようになる。実際には45度回転して√2倍した変換に相当。ABC283 Fでは、マンハッタン距離の最小値をセグ木で求めたので、この問題もいけるのか？練習でやってみたい。その場合、座圧は必要。逆にABC283 Fも45度回転でいけるのか…？ 2023-03-05

037 - Don't Leave the Spice（★5）

x 頭の中で考えて、DPのなかでいもす使ったらいけるんじゃないか？と思って自力ACを狙うも、勘違いだった。勘違いする問題がたくさんあって解けないからこそ、勉強になる。想定解法は、今回の料理で香辛料が合計Wとなる場合、1つ前の料理まででW-RからW-Lの香辛料を使った場合の価値の最大値+Vの価値を生み出せる、というDP遷移を、セグ木で実装するというもの。つまり、貰うDPでないとこの発想にはならない。なんとなく配るDPに偏って思考していると思いつけないことがおもしろい。 2023-03-05

038 - Large LCM（★3）

o C++でオーバーフローの典型らしく、Pythonでは無風。 2023-03-05

039 - Tree Distance（★5）

o これ自力でいけたんですが、結構難しい気がして、成長を感じた。035よりもこっちの方が木DP感ある。と思ったら想定解法と考え方が違った「主客転倒」してエッジの両側の点の個数の積の回数、そのエッジが使われると考えるのか…。天才だなぁ。ぼくは、末端からその頂点まで続く距離と個数を木DPしてた。複雑だ。 2023-03-05

040 - Get More Money（★7）

x 結構おもしろい考察ができたが、実は激ムズ問題だった。ぼくが考えてたのは家iに入ろうと思ったら、そのために入る必要がある家は逆に辿っていけば全部確定するなぁということ。その情報を使ったらなんとかなるかなぁ？と。しかしなんともならず。これは「燃やす埋める問題」と呼ばれるものらしい。しかし「燃やす埋める問題」と聞いてもピンとこなくて頭に入ってこない。Aを燃やしてBを埋める場合はコストがかかりますってなんやねん！と。理解するのに苦労し、なかなかおもしろいアルゴリズムだった。わかってみると「燃やす埋める問題」でもいい気がしてくる。つまり、理解したあとでは、それをそれとわかる名前を付けた方が思考のショートカットに役立つということなのだろう。次のようなグラフを考える。Aを燃やすコストをSからAへのエッジのコストとし、Aを埋めるコストをAからTへのエッジのコストとする。Bを埋めてAを燃やすとかかるコストは、BからAへのエッジのコストとする。最小カットが最小コストなので、最大フロー問題に帰着する。発想があたおかだが…。 2023-03-05

041 - Piles in AtCoder Farm（★7）

o レベル7だが、自力でできた。凸包をすでに過去のABCで履修していたので、なんとかごにょごにょ解けた。凸包の直線上の格子点を求める、というのは初めてだったのでどうしたものかと思ったが、最小公倍数の問題と気づいて、自力で解くことができた。いや、今想定解法見たら、ピックの定理ってなんだ？ぼくは全体を囲む長方形から外側の格子点を順番に引いていって解いた。Python勢の中でかなり速いし、まあいいか。 2023-03-05

042 - Multiple of 9（★4）

o DPでやったけど、考え方が微妙に違っておもしろい。ぼくは合計i-1で最後の桁が1から9までの場合の数を別々に覚えておくと、i桁目が1の場合の数は、i-1桁目が1から9全部の場合の和、i桁目が2ならi-1桁目が1の場合の数（つまり1に1をつなげて2にできるので）、3なら2、…、9なら8、といった具合に計算した。想定解法では、i桁目が1ならdp[i-1]、9ならdp[i-9]といった具合だった。しかし、結局式は同等とわかる。同等だけど、実装に影響が出るのもちょっとおもしろい。ぼくのやり方の方が遅いかもしれない。9の倍数は各桁の和が9の倍数っていうのは小学生のとき知った気がする。あの頃は、9999は9の倍数だから10000は9で割って1余る、みたいな考え方だったっけ。 2023-03-05

043 - Maze Challenge with Lack of Sleep（★4）

x この問題がレベル4とは納得いかない。激ムズで新しい内容でおもしろかった。「拡張ダイクストラ」というらしい。この問題では、曲がることをコストとしているので、曲がらない連続するマスを1つの頂点とし、そこから90度曲がって行ける連続するマスも1つの頂点とし、その間を1のコストでつなぐ。トリッキーだ。ちょっとABC274 Gを思い出した。 2023-03-05

044 - Shift and Swapping（★3）

o

045 - Simple Grouping（★6）

x 15点なので、全頂点間の距離を計算し、小さい順にUnionFindでグルーピングするだけかと思ったが、勘違い。反例は簡単に作れるので反省。これもえげつない問題だった。bitDPで、全部調べてしまう。bitの部分集合全探索がきれいに書けることを知った。このコードでsの部分集合subを全部調べられる。1引くと必ず最下位bitが0になり、その下は全部1になる。もとのsと&を取れば、必ずsubの次に小さい部分集合になる。 2023-03-05

sub = s
while True:
    sub = (sub-1)&s
    if sub == 0:
        break
    # do_something

046 - I Love 46（★3）

o mod 46で考えれば調べる範囲は小さい。46^3 = 97336。 2023-03-05

047 - Monochromatic Diagonal（★7）

x 苦労した。遅くないだろう解法を思いつきウキウキで提出もTLEx7となった。その方法は畳み込みだ。RGB=100とした畳み込みでRRペアをカウントできる。GとBの組み合わせはどうするか？RGB=011から、RGB=010とRGB=001として畳み込んだ結果を引けば良い！GまたはBの組み合わせは、GB+BG+GG+BBなので、GGとBBを引けば、赤に相当するGBとBGが残るではないか！でも処理速度が遅すぎた。Twitterを見ると、みんなZ Algorithmと言ってる。言われてみると確かに、完全一致の問題に帰着できることがわかる。赤の条件は、Rに対応するのがR、Gに対応するのはB、Bに対応するのはGなので、対応する文字列を完全に生成できるからだ。これに気づけなかったのは不覚。しかしZ Algorithmでやり直しても、最初TLEx1だった。想定解はローリングハッシュだったらしく、やってみるとまたTLEx7。なんかPyPyでの文字列処理苦手意識がある。結局、RGBを012とかに置き換えたり、ローリングハッシュのベースを小さくしたり、Z Algorithmも（3,4,5のような絶対に一致しない文字を挟むことによってまとめて処理するため）T+[3]+TR+[4]+TG+[5]+TB、みたいな文字列を作って、一括でやったりして、TLEを解消した。それでも遅いし、本当に苦手意識が取れない。RGBを012に置き換える処理でこれはいいね。 2023-03-06

'RGB'.index(c)

048 - I will not drop out（★3）

o 部分点を取ってからしか残りの点数は取れないが、部分点は残りの点数より大きいので、部分点と残りの点数を全部リストに入れてソートして、でかい順に取っていけばいい。最初プライオリティキューを使って、部分点を取ったら、残りの点をまたプライオリティキューにつっこむというような処理をしていて、答えは正しいが、ちょっと遅かった。 2023-03-06

049 - Flip Digits 2（★6）

o 考えてるうちにすべてのビット間をカバーすればよく、最小全域木と分かった。なかなかすごい。最初、最小コストハミルトン経路じゃない？と思ってビビっていたが勘違いだった。基底を選ぶ方法も同じなんだろうか？ 2023-03-06

050 - Stair Jump（★3）

o

051 - Typical Shop（★5）

x 「半分全列挙」らしいが気づけなかった。2^40は1兆だけど、2^20は100万なので、半分ずつ計算した結果を合わせればいいというもの。ABC271 Fでは、半分ずつやることに気づけたけど、問題が変わるとなかなか気づけない。何度か経験することで身につくことを期待。 2023-03-07

052 - Dice Product（★3）

o 実は全ての面を足してかけるだけ。ぼくにとって、それが当然と思えるようなことではなく、しばらく考えて、そうだなと気づいた。i-1個目までの結果に対して、全パターンに対して、i番目のサイコロの出目をかけてそれを足すのだから、やはり最初からi番目のサイコロの出目を足したものをかけるだけでいい。 2023-03-07

053 - Discrete Dowsing（★7）

o この問題、レベル7だが、自力で解けた。こういうのは2分探索を連想するけど、登って下っているので、1点で得られる情報がない。2点調べてみたらどうか？2点調べると、その2点の上下関係で、どちらかの点の左右に範囲を絞れることがわかる。つまり最悪のケースでも、2つのクエリで約2/3に絞れる。1/3になる場合もある。この方針で15回で求まるかどうか？最悪のケースを想定して手元で実験したらいけそうだったので、提出。問題なくACだった。 2023-03-07

054 - Takahashi Number（★6）

x エルデシュ数みたいな問題。論文の共著者をつなぐグラフで、BFSすれば高橋数は求まるだろう。しかし、共著者が100000人いて完全グラフを作ると破綻してしまう。全く解決策が思いつかなかった。論文という頂点を作り、論文と共著者を結ぶことで、辺の数はN^2からNに減る。えげつないアイデアで、むちゃくちゃ勉強になる。このテクニックは、実はABC277 Fで、経験済みだ。あのときはN点のグループとM点のグループをNxMの全ペアつながなければならないところ、間に頂点を挟んでN+Mに減らしていたのを見て、感動したものだった。なるほど、もう1度同じテクニックに出会ってみると、グラフの辺を減らす典型的な方法だとわかってうれしい。いずれにせよ、感動モノだ。 2023-03-07

055 - Select 5（★2）

o 100個から5個選ぶということで、Googleで100 choose 5を計算すると、75287520だった。意外と少ない。実行時間制限も5秒なので、全探索でよいのだろうと気づいて、解けた。解説によると、定数倍を見積もれというのが、この問題の学びらしい。O(N^5)だから、100^5=100億としてしまうと、確かに解ける気がしない。実際にCombinationを計算した7500万はだいぶ小さい。この問題に限らず、あれ意外と小さいのか？というのはこの典型90で何度も経験している。 2023-03-07

056 - Lucky Bag（★5）

o 全く同じパターンの問題をABCでやったことがある。i日目までに〇〇円買えるかどうか？をDPして、ちょうどS円で買える場合はDPしたマトリックスを遡ればいい。 2023-03-07

057 - Flip Flap（★6）

o ちゃんと勉強してないけど、直感だけでnoshi基底で解いた。おもしろい。以前スキップしたExの問題で、mod 2の連立方程式を解く問題があったと思うので、もう1度チャレンジしてみるつもり。楽しみ。もちろん、関連する理論もちゃんと勉強したい。 2023-03-08

N, M = map(int, input().split())
slist = []
for _ in range(N):
    T = int(input())
    s = 0
    for a in map(int, input().split()):
        s += 1<<(a-1)
    slist.append(s)
goal = 0
for i, a in enumerate(map(int, input().split())):
    if a == 1:
        goal += 1<<(i)
base = []
for a in slist:
    for e in base:
        if a^e < a:
            a ^= e
    if a:
        base.append(a)
        if a^goal < goal:
            goal ^= a
if goal == 0:
    print(pow(2, (N-len(base)), 998244353))
else:
    print(0)

058 - Original Calculator（★4）

o ボタンを押す度に、10^5で割っているので、10^5以下の回数でループに入ることがわかる。普通にできた。 2023-03-08

059 - Many Graph Queries（★7）

x これはえげつない問題だった。頂点IDの昇順にしか辺が張られないので、ダブリングして一致すればいいのかなぁと思ったら、親が2つある場合もあるのか。実は色んなパターンのグラフを経験してなくて、こういうのを見逃してしまうことがある。全く見当がつかないので、解説を見ると、ぼくにとって、全く新奇の解法だった。64bit使って、一気に64個のクエリを処理するのだという。これはエグい。すべての頂点に対して親一覧はわかっているので、親に到達できれるなら、その子には到達できるというDP遷移ができる。で、スタート頂点でqビットを1にし、1からNへ走査し、どんどん伝搬させていってゴール頂点のqビットが1であれば、到達できることがわかる。Pythonでは、64bitだとTLEとなった。30bitに減らしてもTLE。むしろ20000bitに設定してPyPyではなく、Pythonを使うと現在Python勢の中で、最速になった。おもしろい気付き。20000bit整数なんて使ったら遅そうだが、そうではなかった。 2023-03-08

import sys
input = sys.stdin.readline
step = 20000
N, M, Q = map(int, input().split())
parents = [[] for _ in range(N+1)]
for _ in range(M):
    x, y = map(int, input().split())
    parents[y].append(x)
qs = [tuple(a for a in map(int, input().split())) for _ in range(Q)]
amari = Q % step
if amari > 0:
    addition = step - amari
    qs.extend([(1,1)]*addition)
repeat = len(qs) // step
shifts = [1<<i for i in range(step)]
ans = []
for i in range(repeat):
    dp = [0]*(N+1)
    i_ = i * step
    for j in range(step):
        dp[qs[i_+j][0]] += shifts[j]
    for v in range(2, N+1):
        for p in parents[v]:
            dp[v] |= dp[p]
    for j in range(step):
        if dp[qs[i_+j][1]] & shifts[j]:
            ans.append('Yes')
        else:
            ans.append('No')
print(*ans[:Q], sep='\n')

060 - Chimera（★5）

o 最長単調増加部分列が必要になることは、見ればわかる。DPでどうやればいいか？と方針を決めて考えて、セグ木でいけることに気づけてよかった。ただし、別のアルゴリズムがある模様。そちらも勉強する必要がある。 2023-03-08

061 - Deck（★2）

o dequeそのものだった。

062 - Paint All（★6）

x AiとBiの少なくとも一方が白の時に、iを黒く塗ることができる。という問題なのだが、AiかBiを黒く塗ることができると勘違いした。なもりグラフだ！と思って、全くデタラメな回答を実装してしまった。全部黒に塗れるか？ではなく、全部黒の状態から全部白にできるか？を調べる問題として解けば良いらしい。トリッキーな発想。一瞬なんでそれでいいの？と思うけど、黒から白にしていく場合、白にしたことで白にできなくなるボールがないから。どんどん白にしていくだけ。逆にするだけでこんなに簡単な問題になるとは驚きだ。ところで「ボールAi、Biの少なくとも一方が白である時に限り、ボールAiもしくはBiを黒く塗ることができる。」という条件の問題も普通にありそう。最初勘違いしてそれを解いてしまったけど、おもしろくないこともなかったwそれはそれでありそうな問題。 2023-03-09

from collections import deque
N = int(input())
G = [set() for _ in range(N+1)]
used = [False for _ in range(N+1)]
q = deque([])
ans = []
for i in range(1, N+1):
    a, b = map(int, input().split())
    G[a].add(i)
    G[b].add(i)
    if a == i:
        q.append(a)
        used[a] = True
        ans.append(a)
    elif b == i:
        q.append(b)
        used[b] = True
        ans.append(b)
while q:
    cur = q.popleft()
    for next in G[cur]:
        if not used[next]:
            q.append(next)
            used[next] = True
            ans.append(next)
for v in range(1, N+1):
    if not used[v]:
        print(-1)
        break
else:
    print(*reversed(ans), sep='\n')

063 - Monochromatic Subgrid（★4）

o 解けて嬉しい。書いてて楽しいプログラムだったと思う。H<=8という制約が確かに気になる。2^8=256。お、間に合うな。と思えた。bitから部分集合を列挙する処理をさっそく使った。最初1をカウントする時に、3、5、7、、、を集めてくるという処理をあとでやっていて処理が遅かった。3がでてきたときに1にも上乗せしてカウントしておく、というように変更してうまくいった。 2023-03-08

from collections import defaultdict
H, W = map(int, input().split())
plist = [list(map(int, input().split())) for _ in range(H)]
HW = H*W
pow2 = [1]*(H+1)
for h in range(1, H+1):
    pow2[h] = pow2[h-1]*2
counter = [defaultdict(int) for _ in range(HW+1)]
for w in range(W):
    num_bits = defaultdict(int)
    for h in range(H):
        num_bits[plist[h][w]] += pow2[h]
    for n, b in num_bits.items():
        x = b
        while x:
            counter[n][x] += 1
            x = (x-1)&b
popcounts = [bin(i).count('1') for i in range(pow2[H])]
ans = 0
for n in range(1, HW+1):
    if not counter[n]:
        continue
    for b, count in counter[n].items():
        ans = max(ans, count*popcounts[b])
print(ans)

064 - Uplift（★3）

o 2023-03-08

065 - RGB Balls 2（★7）

x なぜかr+g<=Xなどの不等式を見て2-SATを思い浮かべてしまうなぞ現象。r+g+b=Kと合わせて、b>=K-Xと言い換えるのはお見事としか言いようがない。シンプルだけど気づけなかった。3つのうち2つの条件→実は1つの条件に言い換えられる、というのはありがちかも。しかしこの問題が畳み込みを使う問題とは想定外の結果だ。r+bの値ごとのrとbの組み合わせの合計を、一気に求められる。r+bでループできるので計算量がO(K^2)にならない。0未満になってしまうような不正な状態をカウントしないように、ミスして気づくのではなく、始めからちゃんと条件を入れられるのは大事。 2023-03-09

bcoef = np.array([choose(B, b) if K-X <= b <= B else 0 \
                  for b in range(min(B+1, K+1))], dtype=np.int64)
rcoef = np.array([choose(R, r) if K-Y <= r <= R else 0 \
                  for r in range(min(R+1, K+1))], dtype=np.int64)
convret = convolve2(bcoef, rcoef, M)
ans = 0
for g in range(K-Z, G+1):
    rb = K-g
    if rb >= 0:
        ans += convret[rb] * choose(G, g)
        ans %= M
print(ans)

066 - Various Arrays（★5）

o できた。が間に合うと思わなかった。この問題の計算量、100^4=1億ではないか？でも実行してみると72ms。他の余計な処理がほとんどないようなプログラムだからだろうか？わからないものだ。累積和の累積和とか使ったんだけど、誰もそんなことに言及してない。みんな「期待値の線形性」としか言ってない。ぼくはそこは何も迷わないのだが。 2023-03-09

N = int(input())
bigsum = [[0]*(103) for _ in range(N)]
bigsumsum = [[0]*(103) for _ in range(N)]
ws = [0]*N
ans = 0
for i in range(N):
    l, r = map(int, input().split())
    cur_width = r - l + 1
    ws[i] = cur_width
    diff = 0
    for j in range(l, r+1)[::-1]:
        diff += 1
        bigsum[i][j] += diff
    for j in range(1, l)[::-1]:
        bigsum[i][j] += diff
    for j in range(1, r+1)[::-1]:
        bigsumsum[i][j] += bigsumsum[i][j+1] + bigsum[i][j]
    for j in range(i):
        ans += (bigsumsum[j][l+1] - bigsumsum[j][r+2]) / (ws[j]*cur_width)
print(ans)

067 - Base 8 to 9（★2）

o レベル2。なんか好き。8進数として読み込むのは初めてで、intの第2引数に基数を入れると、8進数として解釈するらしい。int(input(), 8)最後の出力も8進数なので、f'{N:o}'とした。というわけで、ちょっとハイペースで強迫神経症的に典型90をやり続けているので、強制的に1週間くらいストップして他のことをやる！問題見るの禁止！ 2023-03-09

N, K = input().split()
N = int(N, 8)
K = int(K)
pow8 = [1]*20
for i in range(1, 20):
    pow8[i] = pow8[i-1] * 8

def step98(n):
    ret = 0
    k = 0
    while n:
        x = n % 9
        if x == 8:
            ret += pow8[k] * 5
        else:
            ret += pow8[k] * x
        n //= 9
        k += 1
    return ret

for i in range(K):
    N = step98(N)
print(f'{N:o}')

068 - Paired Information（★5）

o xとyの間が全部つながっていれば計算できる。インデックス0と1、2と3、4と5の和から1と2、3と4の和を引くと0と5の和を計算できる、みたいなのを偶数番目か奇数番目かなどのめんどうな条件分岐をちゃんと書いて、セグ木でやって解いた。解説を見ると、T=1のときつながってるかどうかだけ最初に処理してAmbiguousを確定し、あとはクエリ先読みで全部判明した状態でやってるみたい。アイデアとして。 2023-03-18

N = int(input())
Q = int(input())
even = SEGT(N)
odd = SEGT(N)
count = SEGT(N)
ans = []
for _ in range(Q):
    t, x, y, v = map(int, input().split())
    if t == 0:
        count.set(x, 1)
        if x&1:
            odd.set(x, v)
        else:
            even.set(x, v)
    else:
        if y == x:
            ans.append(v)
            continue
        diff = y - x
        if diff > 0 and count.query(x, y) == diff:
            if y&1:
                ans.append(even.query(x, y) - odd.query(x, y) - (v if diff&1 else -v))
            else:
                ans.append(odd.query(x, y) - even.query(x, y) - (v if diff&1 else -v))                
        elif diff < 0 and count.query(y, x) == -diff:
            if y&1:
                ans.append(odd.query(y, x) - even.query(y, x) - (v if (-diff)&1 else -v))
            else:
                ans.append(even.query(y, x) - odd.query(y, x) - (v if (-diff)&1 else -v))
        else:
            ans.append('Ambiguous')
print(*ans, sep='\n')

069 - Colorful Blocks 2（★3）

o 最初はK通り、次は違う色だからK-1通り、3つ目以降は直前の2と違う色だからK-2通り。というのをかけていく。瞬殺という感じでもないの反省。 2023-03-18

070 - Plant Planning（★4）

o マンハッタン距離の和は、x方向の差の和とy方向の差の和を別々に計算できるので、それぞれ最小になるような位置を確定すれば良いが、ソートして真ん中を取れば良いとわかる。ある値mより小さいのが7個、大きいのが5個あるとすると、mをm-1にしたら差の合計は2減るので…。真ん中だとどっちに動いてもプラマイ0。なのでx、y両方向真ん中でOK。 2023-03-18

071 - Fuzzy Priority（★7）

x しっかり考えないと解けない感じで長考した。DFSであると。しかしトポロジカルソートもDFSだから頭がこんがらかってしまう。Kahnのトポロジカルソートで、入力が無くなった頂点のセットから順番に取り出すが、その時にどれを取り出すか？で状態を分岐していくようなDFSをする。なので1つ上の次元で眺めないといけないのが難しい。で、そのDFSで管理すべき状態とは、それまでに決定したトポロジカル順序、次選べる頂点リスト、入力頂点のリストなので、全部サイズはN。DFSの深さはトポロジカル順序なので当然N。よってO(N^2)になってしまうので、状態をDFSのスタックに保持できず、困ってしまう。そこで、各深さにおける状態を保持せず、1箇所で管理し、状態遷移に最小限必要な情報だけスタックに積んで、それを使って進んだり戻ったりする。ぼくの考えぬいた最小限の情報は、n個目の順序を決めるときに、次選べる頂点リストの何番目を使ったか？ということだけだった。これで行きがけと帰りがけに適切に処理することでACできた。処理時間は1253msで、Python勢の中で速い方で満足。 2023-03-18

N, M, K = map(int, input().split())
G = [[] for _ in range(N+1)]
pcount = [0]*(N+1)
torder = [0]*(N+1)
for _ in range(M):
    a, b = map(int, input().split()) # [a] < [b]
    G[a].append(b)
    pcount[b] += 1
starters = [v for v in range(1, N+1) if pcount[v] == 0]
left = K
dfs = []
for i in range(len(starters)):
    if left:
        dfs.extend([[~1, i], [1, i]])
        left -= 1
ans = []
while dfs:
    n, i = dfs.pop() # select i-th for n-th
    if n >= 0:
        starters[i], starters[-1] = starters[-1], starters[i]
        v = starters.pop()
        torder[n] = v
        if n == N:
            ans.append(torder[1:])
            continue
        for u in G[v]:
            pcount[u] -= 1
            if pcount[u] == 0:
                starters.append(u)
        if starters:
            dfs.extend([[~(n+1), 0], [n+1, 0]])
        j = 1
        while left and j < len(starters):
            dfs.extend([[~(n+1), j], [n+1, j]])
            left -= 1
            j += 1
    else: # post order
        n = ~n
        v = torder[n]
        # deselect v
        removeset = set()
        for u in G[v]:
            pcount[u] += 1
            if pcount[u] == 1:
                removeset.add(u)
        while starters and starters[-1] in removeset:
            starters.pop()
        starters.append(v)
        starters[i], starters[-1] = starters[-1], starters[i]
if left or not ans:
    print(-1)
else:
    for a in ans:
        print(*a)

072 - Loop Railway Plan（★4）

o 結構難しい。最大16頂点だから小さいなとは思ったけど全探索でいいとすぐに思わなかった。bit全探索で使う頂点を決めてから調べると速かったりしない？とか余計なこと考えてしまう。実は071を簡単にしたような感じの問題で、解説には「バックトラック」という言葉が書いてあった。行けなくなったら戻る。この問題では071ほど複雑ではなく、1歩戻るのは、そのマスをまだ通ってないことにするだけだ。グラフ化するときは、左上から調べていって、右と下につなげられるか調べていく。全方位調べたらエッジが2重になっちゃう。DFSといっても1つ見つけて終わればいい問題が多い。この071と072を通じて「バックトラック」しながらDFSで全探索する問題に触れられたのは良かった。意外とやってなかった。 2023-03-18

used = [False]*HW
ans = -1
for v in range(HW):
    if G[v]:
        stack = [(~v, 0), (v, 0)]
        used[v] = True
        while stack:
            cur, d = stack.pop()
            if cur >= 0:
                for nex in G[cur]:
                    if not used[nex]:
                        stack.extend([(~nex, d+1), (nex, d+1)])
                        used[nex] = True
                    elif nex == v and d >= 3:
                        ans = max(ans, d+1)
            else:
                cur = ~cur
                used[cur] = False
print(ans)

073 - We Need Both a and b（★5）

x 最後の連結成分が1色か2色かで場合分けして木DPをやってたら、ロジックが破綻しそうになってしまい、たまらず解説見た。赤と青も分けていたのでそのようにすると整理できたけど、改めて見ると、最初単に詰めが甘くて破綻しただけで、1色か2色かで分けた方が効率的でよかった。最初の勘違いはどうも、遷移の過程で1色だけの連結成分も発生してしまうのではないか？という疑問を持ち続けていたためっぽい。作らないように遷移するから気にしなくていい、というところまで到達できずにギブアップしてしまった。こういう思考のミスってたまにやらかしてそうで、成績伸ばすために乗り越えなければいけない反省点。 2023-03-19

場合分け考察メモ

M = 10**9 + 7
N = int(input())
clist = input().split()
G = [[] for _ in range(N)]
for _ in range(N-1):
    a, b = map(int, input().split())
    G[a-1].append(b-1)
    G[b-1].append(a-1)
parent = [-2]*N
stack = [-1, 0]
dpa = [0]*N
dpb = [0]*N
dpab = [0]*N
parent[0] = -1
while stack:
    cur = stack.pop()
    if cur >= 0:
        for nex in G[cur]:
            if parent[nex] == -2:
                parent[nex] = cur
                stack.extend([~nex, nex])
    else:
        cur = ~cur
        a_b_ab = []
        for nex in G[cur]:
            if nex == parent[cur]:
                continue
            # nex = child
            a = b = ab = 0
            if clist[cur] == 'a':
                a += dpa[nex] + dpab[nex]
                ab += dpab[nex] + dpb[nex]
            if clist[cur] == 'b':
                b += dpb[nex] + dpab[nex]
                ab += dpa[nex] + dpab[nex]
            a_b_ab.append((a%M, b%M, ab%M))
        if a_b_ab:
            a, b, ab = a_b_ab[0]
            total = a + b + ab
            for i in range(1, len(a_b_ab)):
                a_, b_, ab_ = a_b_ab[i]
                a *= a_
                b *= b_
                total *= (a_ + b_ + ab_)
                a %= M
                b %= M
                total %= M
            dpa[cur] = a
            dpb[cur] = b
            dpab[cur] = (total - a - b) % M
        else: # leaf
            if clist[cur] == 'a':
                dpa[cur] = 1
            elif clist[cur] == 'b':
                dpb[cur] = 1
print(dpab[0])

074 - ABC String 2（★6）

o ひらめいた。解説の方法っぽくはない。i番目をc->b、b->aにするとき、i-1番目までがa->b、b->c、c->aになるということで、i-1番目までは操作できる状態にしたり（a->b）、回数を増やせたり（b->c）できると考えられる。c->aは操作できなくなるので、cがある状態で、上の桁を操作するのはもったいないと考える。事前にその桁に対して操作し、c->bとしておけば、その1回操作できる上に、またcに戻せるのだから。以上より、操作するときはその下の桁を全部aにしてからが良いとわかる。頭の中でイメージができあがるとおもしろい。 2023-03-22

075 - Magic For Balls（★3）

o 素因数の数がわかればいける。 2023-03-22

076 - Cake Cut（★3）

o しゃくとり法でいける。 2023-03-22

077 - Planes on a 2D Plane（★7）

x 2部グラフ最大マッチングであることまでわかったけど、最後の方の重いテストケースで、TLEx9が取れなかった。他の人の回答を見ていて、AとBを両方座標でソートしている人が多く見られ、そのようにするとACできた。ソートする必然性がしっくりきていないが、左端から順に優先的にフローを流すことで、流し戻しの発生率が下がるんだろうか？っていうのが仮説。それだけで何倍も速くなるのであれば驚きだ。時間制限が1.5秒で、かなり厳しく設定してあった。ソート後は500ms台で通った。 2023-03-23

078 - Easy Graph Problem（★2）

o 2023-03-22

079 - Two by Two（★3）

o 左上から貪欲にやるだけ。 2023-03-22

080 - Let's Share Bit（★6）

o 数字がa1つだとどうだろう？と考えると、全体集合の数2^Dから、aの0のbitしか使わない数字の数を引いて計算するだろう。ではa,b2つの数字だった場合は？全体からaの0のbitしか使わない数字の数とbの0のbitしか使わない数字の数を引いて、aもbも0のbitしか使わない数字の数を足せば良いとわかる。同様に3つの組み合わせは引く、4つの組み合わせは足す、ということを繰り返せば答えが導けるとわかる。計算量が大丈夫か？気になるが、Nが20以下なので、その中の数字の組み合わせは2^20=約100万通り以下なので、全部計算できる。Python勢4番目の162msでうれしい。 2023-03-25

081 - Friendly Group（★5）

o 2次元座標系でKxKの中に入る最大点数と考えると、極めて典型的に思えるのにわからない！と、悩んだが、ひらめけた。5000以下の自然数のみなので、25000000個に収まるのか。2次元累積和で全部調べた。 2023-03-23

082 - Counting Numbers（★3）

o しんどいけどOK。 2023-03-23

083 - Colorful Graph（★6）

x 難しい問題だった。「平方分割」というテクニックを使う。1つの頂点に200000頂点が隣接していて、毎回それを更新されると、色変更の計算量がO(NQ)で400億にもなってしまう。そこで、次数が大きいものに対してだけ直で色を変更し、次数が小さい頂点の色は、自身と周囲の頂点にいつ色変更クエリが来たか？を保存しておき、最後の更新の色から色を判定することとする。次数の境界値をBとすると、次数の大きな頂点数は最大2M/Bなので、隣の頂点にクエリが飛んだときにその隣の次数が大きな頂点の色を変更するコストは2M/Bと見積もれる。次数が小さい頂点はその次数分周囲の頂点のクエリタイミングを確認する必要があるので、コストはB。よって2M/B + Bを最小化するには、B = √2Mとわかる。結局計算量は2Q√2Mなので、O(Q√M)となる。√200000=447。重くね？と思うがw 2023-03-25

084 - There are two types of characters（★3）

o DPでやった。難しい木DPだった073の簡単ケースでは？ 2023-03-25

085 - Multiplication 085（★4）

o a, bは√K以下なので、K=10^12でも100万回の計算で全候補が得られる。約数は少ないのでa,b全探索し、割り切れる場合はc=K//(a*b)。a<=b<=cとなるものをカウントすればよい。難しい。あと5問。やめたい。 2023-03-25

086 - Snuke's Favorite Arrays（★5）

o ひらめけた！N=12ということで、ビットごとに全探索すると2^12通りに条件50個、それが60桁だから計算量1200万で済むなーと気づけた。2^60未満の数字を全探索できないにも関わらず、1桁ずつなら全探索できるのはぼくの頭の中でそこまで自明ではないけれど。処理時間も100msと速めでうれしい。 2023-03-27

087 - Chokudai's Demand（★5）

o 不安ありつつもひらめいた方法で正解できた！ワーシャルフロイド+2分探索。ワーシャルフロイドの計算量はO(N^3)だけど、N=40なら64000、10^9の2分探索してもせいぜい50回とかで済むなら計算量は少ない。最初に読み込んだ距離のリストを2分探索の評価時にコピーするために、import copy、copy.deepcopy(dist)として深いコピーを初めて使った。あと、i,jの組み合わせ数が0になるものと、Infinityになるものの条件で若干ハマったので注意。あと3問！自力で解けていい調子だがバテバテw 2023-03-27

088 - Similar but Different Ways（★6）

x 解けず。DFSで間に合う気がしなかった。まさにこの典型90の、071、072で学んだ、バックトラックで状態を元に戻す処理をやりながらDFSでの列挙。ここで学んだのだから解きたかった問題だ。両方選んではいけないペアの処理が重いのではないか？と思ったがN=88なので、1つのカードを選んだとき、選べなくなるカードが最大88枚。カードを選ぶ度にO(N)でかかってくるが、よく考えたら大して重い処理ではなかった。重いと錯覚してしまって無念。これ2-SATで連結成分を上からTrueにしていくのでは？とか複雑なこと考えてしまってたw 2023-03-29

089 - Partitions and Inversions（★7）

o バテバテでしんどくなってたけど、考えてたら、イケるじゃん！となって、1回目の提出でAC！バブルソートの交換回数は転倒数の数と同じと気づいた。なぜなら転倒を解消するのが交換であり、交換が終わると転倒は0になるからである。。。大小関係しか見なくていいので、数列を座圧したものをフェニック木に突っ込んで、しゃくとりしながら、次追加する数字より大きいのがいくつあるか？消す数字より小さいのがいくつあるか？で区間の転倒数を更新していく。転倒数がK個以下の区間を考慮しながらDP。さらにDPを累積和。累積和使わないとTLEだった気がするので、事前に気づけたのは良かった。というわけで、ついにあと1問！ 2023-03-30

気まぐれ時系列

2022-08-27

ABC266。初参加。なんでいきなり参加したのか？「Wordleをやっててふと思いついた問題をPythonで解く」というPython関連の記事を書いたときにnoteで#Pythonタグが付いてる記事をテキトーに読んでたら、AtCoderの記事がいくつかあって興味を持った。ググりながら、ミスりながらやっていたが、ビギナーズラックで、4完できてしまう。その後、なかなかこのときのAC数にたどり着けない。最初の頃はよくわかっていなかったので「解説あるんだから、コンテスト終了後、ExもACして勉強するんでしょ」と思っていたが、実は無謀だったということは、徐々に知ることとなる。それに気づくまで、最初の3回はExをACした。1ヶ月かけてFFTを理解したりと疲弊したが、あれで何かスイッチが入ったかもしれない。

2022-10-01

ABC271。4回目にして、AC数最低記録、2完。しかし入茶する。

2022-10-22

ABC274。2ヶ月近くかかって、ようやく初参加以来の4完。ずっと4完が目標だった。

2022-10-29

ABC275で、初めての5完を達成。

2022-11-26

ABC279で入緑。

2022-12-10

参加した過去12回のAC数推移。4,3,3,2,3,4,5,4,4,5,5,4。

2022-12-13

火曜日。日曜日に、前日参加したABC281の問題Fを、初めて解説を見ずに自力でAC。不思議なことに、続けてABC268とABC267の問題Fを解説を見ずにAC。3日間で急に問題Fを3つ、自力で解けた。ABC267 Fなんて、木の直径という概念知らなかったけど、解くためにそれが必要だと思い、正しい求め方も自分で導いてACした。なお、問題Gを1問でも自力で解くのが、現在の目標。参加し始めてから、問題を解くたびに毎回毎回新しいテクニックが出てきてそのクレイジーさ、あたおかさに度肝を抜かれ続け、もはや中毒的に続けており、やめられなくなってしんどい。1つ解いたら次の問題を読んでしまう。しんどいので「何も考えずに寝たい」とも思う。数学も趣味として手を伸ばし始めている。

2022-12-16

これまでに参加したABCの、問題GまでのACを完了。最後に解いたABC266 Gで初めて問題Gを自力AC。比較的易しかったけど、心構えには影響がありそう。ABC273のとき、京都に行っていて、ABC273は唯一ノータッチ。気が向いたらやる。

2022-12-21

ABC282 CのTLE問題、Pythonのstrを結合するとき、パフォーマンスを意識する場面で+=を使うのはNGで、''.join()を使うべきらしい。PEP 8なる文書に記載されている。三ヶ月半もやってて知らなかったことにショックを受ける。

2023-01-08

新年最初のABC284。4回ぶり4度目の5完。参加した過去15回のAC数。4,3,3,2,3,4,5,4,4,5,5,4,3,4,5。

2023-01-14

過去に解いたABCの問題を一通り見直した。2回見ても難しいし、2度と考えたくないような問題がいくつもあるなぁという感想。頭がパンク。ユークリッドの互除法と拡張ユークリッドの互除法を勉強した。ユークリッドの互除法は極めて有用なアルゴリズムだし、紀元前300年に記述されたことに驚く。👀より、LCPとは何か？Suffix Arrayの[i]と[i+1]のprefixの一致長のリストらしい。使ったことないけど、ずっと調べてなかったのでスッキリ。今日は土曜日にARC153が開催されたので、初めてARCに参加してみた。1完で洗礼を受けた。

2023-02-02

3日くらい読み続けて、APG4bを修了（EX26除く）。とても勉強になった！いきなり本番でC++移行できるわけもなく、典型とかACLコンテストで練習を積み重ねて、いけそうと思ったら、本番で使ってみようと思う。早く使いたい。

2023-04-15

今日は、ABC298でした。このnoteを書いてるうちに入水し、タイトルを入水編に変更した上で、次のnoteを作ろうと思ってがんばってきましたが、入水できる気がしないので諦めます。このnoteはすでに文字数制限に引っかかっていて、重要でないコードや画像を消しながら更新してたんですよね。フラストレーションが溜まる作業だったので、このnoteは入緑編とし、スッキリと次のnoteに移動しちゃいます！ちなみにABC298はDDosが原因で、Unratedとなるとのこと。ホッとしてるのですが。笑。

【ABC289】DDoSの影響が続いており、アクセスしづらい状態が続いているため、このコンテストはUnratedとさせていただきます。申し訳ありません。このコンテストではRatingの変化が起こりません。
コンテスト自体は有効ですので、終了まで問題のネタバレ等はお控えください。

— AtCoder (@atcoder) April 15, 2023

👀

ABC276 Ex 連立方程式
OEIS
畳み込みのライブラリ化
典型90 005 畳み込み
C++ permutation
HLD
平衡二分探索木
中国剰余定理ロジック
高速ゼータ変換