見出し画像

因果推論入門： 釣果が高くなるのはルアーか生餌か？

株式会社ANGLERS

こんにちは、ANGLERSのエンジニアのリッキーです。このたびはブログを執筆する機会を頂戴し、長らく積読となっていた以下の因果推論に関する書籍に取り組むことにしました。

正直なところ、難易度が高く、一読しただけでは完全に理解することができなかった部分も少なくありません。しかし、理解できた範囲内で、自身の理解を深めるとともに、備忘録としてのまとめを試みたいと思います。


因果推論とは？その必要性について

因果推論は、ある施策が目標とする指標にどのような影響を及ぼすかを推定する手法です。例を挙げると、

  • バナーを変更したことがクリック率にどう影響するか

  • ページ表示速度を改善したことがユーザーの滞在時間にどう影響するか

などがあります。このように、バナーの変更や速度の改善などの特定の施策を実施した際に、クリック率や滞在時間などの目標指標がどのように変化するかを理解し、この変化の関係性を「因果」と定義します。

そして、この因果関係を明らかにすることが、因果推論の主な目的となります。

このような施策と期待される効果を定量的に推定する手法は、あらゆる業務に応用可能であり、ビジネスにおいて非常に重要なテーマと言えそうですね。より具体的なケースを想定して、因果推論の必要性を認識していきましょう。

ケーススタディ①：「メルマガ施策の効果とは？」

本音の口コミが集まる釣具ECサイト「TACKLE BOX」

ここで架空のケーススタディを考えてみます。

Aさんは、とある釣具ECサイトのマーケティングチームのリーダーです。Aさんは、チームメンバーのBさんから、Bさんがテスト的に行ったマーケティング施策について、次のような報告を受けました。

  • 販売促進のための施策検証として、ユーザー全員にECサイトに関するメルマガを配布した。

  • このメルマガには細工がされていて、メルマガを開封したかどうかをユーザーごとに計測可能。

  • メルマガ送信より一週間後、過去一週間分（つまりメルマガ送信から一週間の期間）の購入データを集計したところ、メルマガを開封したユーザーの購入金額が、未開封のユーザーに比べて平均して2.5倍も高くなっていた。

  • このようにメルマガ送信には売上向上に大きなプラスの効果があるので、今後はマーケティングチーム全体として、正式な施策として実施していきたい。

Aさんは、Bさんからの報告をどのように受け取るべきでしょうか？

Aさんは、以下のようにBさんに問いを投げかけました。

  • メルマガを開封してくれるということは、そのユーザーは、もともと私たちのECサイトに興味がある（ロイヤリティが高い）傾向が高いのではないか？

  • であるとしたら、開封したユーザーが、そうでないユーザーに比べてサイトでの購入金額が高くなるのは自然なことであり、仮にメルマガを開封していなかったとしても、同じ結果だったのではないか？

  • メルマガ開封の有無が、売上向上に及ぼす影響を正確に測るには、サイトに対するロイヤリティの影響を排除した上で計測する必要があるのではないか？

Aさんの指摘は的を射ているように感じます。

では、Bさんはどのようにメルマガ施策の効果を測定し、どのようにAさんに報告すべきだったのでしょうか。上記のケースで起こっていることを図で整理してみます。

今回の施策において、【メルマガ開封】が【購入金額】に与える効果を知りたい状況です。

（正確には、開封の有無というよりはメルマガを送ること自体が購入金額に与える効果を知りたいところですが、話を簡単にするために、メルマガ開封の有無にフォーカスします）

「メルマガ開封」が「購入金額」にどのような影響を及ぼすかを知りたい

しかし、Aさんの指摘のとおり、ユーザーごとに異なる【サイトに対するロイヤリティ】が存在し、この【サイトに対するロイヤリティ】が、【メルマガ開封】と【購入金額】の両方に影響を与えており（①および③の矢印）、本来知りたい【メルマガ開封】の【購入金額】に対する影響（②の矢印）を測れない状況になっています。

「サイトに対するロイヤリティ」の影響

このようなシーンで、②の効果の推定に必要となるのが因果推論になります。後述する因果推論の手法を用いることで、③の矢印による影響を考慮しながら、純粋な②の矢印の影響（効果）を測ることができます。

ケーススタディ②：「釣果が伸びるのは生餌？それともルアー？」


釣果が伸びるのは生餌とルアーのどちらか？

次に、別のケーススタディとして、もう少し複雑なケースを考えてみます。

ある釣り場において、【餌タイプ（生餌 or ルアー）】が【釣果】に及ぼす影響について調べたいとします。言い換えると「釣果が上がりやすいのはルアーと生餌のどちらなのか？」を調べたい状況です。

このケースで考慮すべき変数として【性別】と【年齢】を用いて、【餌タイプ】が【釣果】に及ぼす影響を考えてみます。

ここで仮に、

  1. 女性のほうが男性よりもルアーを使う傾向が高い：【矢印①-aの影響】

  2. 年齢が低くなるほどルアーを使う傾向が高い：【矢印③-aの影響】

  3. 男性の方が女性よりも釣果が高くなる傾向がある：【矢印①-bの影響】

  4. 年齢が高くなるほど釣果が高くなる傾向がある：【矢印③-bの影響】

という傾向があると仮定します。

また、今回調査した釣り場は、生餌よりもルアーの方が釣果が上がりやすい状態であったとします。

ここで、矢印③（性別や年齢が釣果に直接及ぼす影響）を考慮せず、単純に釣果データと餌タイプの関係を調べてしまうと、釣果の高い傾向にある【男性】や【年齢高め】の釣り人の多くがルアーではなく生餌を使っていることより、「生餌の方がルアーよりも釣果が高くなりやすい」という「完全に誤った結論」を導いてしまいます。

このようなシーンでも、③の矢印による影響を考慮しながら、純粋な②の矢印の影響（効果）を図るために因果推論が必要となります。

相関と因果の違い

因果推論の手法に入る前に、相関と因果の関係ついてまとめます。

「相関」とは、ある2つの要素が関係しあっている状態です。

例えば、身長と体重には正の相関（身長が高いと、体重も高い傾向）があり、喫煙量と寿命には負の相関（喫煙量が増えると早死にする傾向）があります。

ただし、これらは【原因】と【結果】の関係にはなってはいません（例えば身長が伸びる原因は、体重が重くなることではありませんし、寿命を決定する直接的な原因が喫煙量とも言えません）

一方、「因果」とは、2つの要素の間において、【原因】と【結果】の直接的な関係がある状態のことです。

例えば、喫煙と肺がんリスクには因果関係があると認識されていて、長期にわたる喫煙【原因】によって、肺がんリスクが高まる【結果】ことが医学的に知られています。

「因果」は「相関」の部分集合

「因果」がある場合は「相関」がありますが、「相関」があっても「因果」があるとは限らない点に注意です。

少し混乱してきたので、ChatGPTに聞いたら、安定の分かりやすい回答をくれました

『疑似相関に注意』

次に、因果推論で注意すべき「疑似相関」について見ていきます。例えば、国ごとの【アイスクリームの消費量】と【犯罪率】には正の相関があると言われています。

【アイスクリームの消費量】と【犯罪率】には正の相関があるが、、、

しかし、これは「アイスクリームを食べると、犯罪を犯しやすくなる」という訳でも、「犯罪を犯すと、アイスクリームが食べたくなる」という訳でもありません。

「アイスクリームを食べると、犯罪を犯しやすくなる」という因果は存在しない
「犯罪を犯すと、アイスクリームが食べたくなる」という因果も存在しない

ではなぜ、因果関係のない両者の間に相関が生まれているのでしょうか？
実は、この相関には、国ごとの【平均気温】が関係していて、

  • 【平均気温】が高くなると、【アイスクリームの消費量】 が増える（これは当然な結果）

  • 【平均気温】が高くなると、【犯罪率】が高くなる（これも何となく想像がつきますね）

という関係（因果）より、結果として「アイスクリームの消費量が多い国は、犯罪率も高い」という関係（相関）が生まれることになります。

相関の中でも、この例のように、直接の因果関係のない2つの変数（【アイスクリームの消費量】と【犯罪率】）に相関が生まれる場合、これを「疑似相関」と呼びます。

また、このように疑似相関を産む要因となっている因子（今回の例では【平均気温】）を「交絡因子」と言います。

因果推論を行う際には、このような因果と相関の違いを理解し、疑似相関によって誤った結論を導かないように注意が必要です。

因果推論の理論

さて、因果推論の概念や必要性を説明してきましたが、ここからは因果推論を実際に行うための理論について見ていきます。

求めたいのはATE（平均処置効果）

基本的に因果推論で求めたいものは、「ある施策（＝処置）を実施した際に、狙った数字がどのように変化するか」でした。

ここで、

  • ある処置を変数$${Z}$$として、狙った数字を変数$${Y}$$とします。

  • とある個人の「$${i}$$さん」において、処置が実行されなかった場合を$${Z^i=0}$$として、処置が実行された場合を$${Z^i=1}$$とします。

  • $${Z^i=0}$$の場合の$${Y^i}$$を$${Y^i_0}$$とし、$${Z^i=1}$$の場合の$${Y^i}$$を$${Y^i_1}$$とします。

とすると、個人レベルの処置（施策）の効果は

$$
Y^i_1 - Y^i_0
$$

で表され、これを個体レベルの処置効果（ITE: Individual Treatment Effect）と言います。

いま求めたいのは施策全体の集団レベルの処置効果であり、これを平均処置効果（ATE: Average Treatment Effect）といい、以下のように計算できま
す。

$$
ATE = E(Y_1-Y_0) = E(Y_1) - E(Y_0)
$$

ここで$${E()}$$は期待値であり、集団が$${N}$$人の場合は、

$$
ATE = \frac{1}{N} \sum_{i=1}^N(Y_1^i) - \frac{1}{N} \sum_{i=1}^N(Y_0^i)
$$

で計算されます。

ただし、ここで重要なポイントとして、「$${Y^i_0}$$と$${Y^i_1}$$は同時には存在し得ない」という点です。

つまり「$${i}$$さん」が処置を受けた場合（$${Z^i=1}$$の場合）、$${Y^i_1}$$は存在するが、$${Y^i_0}$$は存在せず、反対に「$${i}$$さん」が処置を受けなかった場合（$${Z^i=0}$$の場合）、$${Y^i_0}$$は存在するが、$${Y^i_1}$$は存在しません。

これは、「ケーススタディ①：メルマガ施策」の事例で言えば、「$${i}$$さん」がメルマガを開封していた場合（$${Z^i=1}$$の場合）、$${Y^i_1}$$である「$${i}$$さんがメルマガを開封した場合の購入金額」は観測できますが、$${Y^i_0}$$である「$${i}$$さんがメルマガを開封しなかった場合の購入金額」は実在しないケース（「反実仮想」という）のため観測することできません。

ここで、実際に観測できた変数を「結果変数」と言い、実在せず観測できない変数を「潜在的結果変数」と言います。

つまり、上記の式のままではATEを計算することが出来ず、何らかの工夫が必要となります。

『ATTとATU』

因果推論でATE以外でよく利用される指標として、ATTとATUがあります。
ATTは、処置群平均処置効果（Average Treatment effect on the Treated）のことであり、

$$
ATT=E(Y_1-Y_0|Z=1)
$$

で表されます。$${E(|Z)}$$は条件付き確率（期待値）の記法です。式からもわかるようにATTは、処置群（処置を受けた人々）における処置の効果を表します。

メルマガ施策の例でいえば、「メルマガを開封した人々の購入量」と「メルマガを開封した人々において、仮に開封していなかった場合の購入量」の差がATTなります。

一方、ATUは、対照群平均処置効果（Average Treatment effect on the Untreated）のことであり、対照群（処置を受けなかった人々）における処置の効果を表します。

$$
ATU=E(Y_1-Y_0|Z=0)
$$

メルマガ施策の例でいえば、「メルマガを開封しなかった人々において、仮に開封していた場合の購入量」と「メルマガを開封しなかった人々の購入量」の差がATUなります。

メルマガ施策の事例において、BさんがAさんに対して「施策には効果がある」の根拠として示そうしたのは「処置群と対照群の単純な平均値の差」であり、数式で表すと、以下になります。

$$
E(Y_1|Z=1) - E(Y_0|Z=0)
$$

これは、ATE、ATT、ATUのいずれでもないことが分かります。

つまり、多くのケースにおいて、このような「反実仮想を考慮しない単純な平均値の差」は、施策の効果を表すのに適切な指標ではなく、バイアスを含む数値を報告してしまっていることになります。

介入による因果の調整

次に「介入」という概念について説明します。

$${Z=0}$$であるものを$${Z=1}$$に変化させたり、$${Z=1}$$であるものを$${Z=0}$$に変化させることを変数$${Z}$$に対する介入と言います。つまり、介入によって反実仮想を考慮することが可能となり、数式としては、

$$
do(Z=1)
$$

のように書きます。この$${do()}$$を介入操作またはdoオペレーターと言います。

ここで、$${E(　|Z=1)}$$と$${E(　|do(Z=1))}$$の違いを整理しておきましょう。

$${E(　|Z=1)}$$は条件付き期待値であり、全データの中から$${Z=1}$$のデータに絞った期待値である一方で、介入操作である$${E(　|do(Z=1))}$$は、全てのデータに対して、$${Z=1}$$という状況を強制的に与えた場合の期待値となります。

メルマガ施策の例でいえば、$${E(　|Z=1)}$$では、メルマガを開封した人々に限定した期待値を求める一方で、$${E(　|do(Z=1))}$$は、全てのユーザーがメルマガを開封するよう操作された場合の期待値を求めることになります。

これを図で考えると、介入操作によって、【サイトへのロイヤリティ】に限らず、【メルマガ開封】の要素が$${Z=1}$$に固定されるため、【サイトへのロイヤリティ】から【メルマガ開封】に向けた①の矢印を消すことができます。

元々の要素の関連
介入操作によって関連をシンプルにできた

また、ここで重要な点が、$${E(　|Z=1)}$$と$${E(　|do(Z=1))}$$は異なるものですが、$${E(Y_1)}$$と$${E(Y_1|do(Z=1))}$$は同じということです。

これは、そもそもの定義として、$${Z^i=1}$$の場合の$${Y^i}$$を$${Y^i_1}$$としている点からも明らかです。同様に$${E(Y_0)}$$と$${E(Y_0|do(Z=0))}$$は同じになります。

これより、ATEは、

$$
ATE = E(Y_1) - E(Y_0)
$$

で表されていましたが、これを介入操作を用いて、

$$
ATE=E(Y_1|do(Z=1))-E(Y_0|do(Z=0))
$$

と表すことができます。

調整化公式でATEを計算可能に

前節で介入操作によって、一部の影響（因果）を消すことができました。しかし$${do()}$$のような介入はそのままでは数学的に計算することができないため、工夫が必要です。

ここで、介入前の世界と、介入後の世界は別であり、それぞの世界での確率をそれぞれ$${P()}$$および$${P_m()}$$で表すとします。

図示すると以下のようなイメージです。

介入前の世界。確率をP()で表す
介入後の世界。確率をP_m()で表す

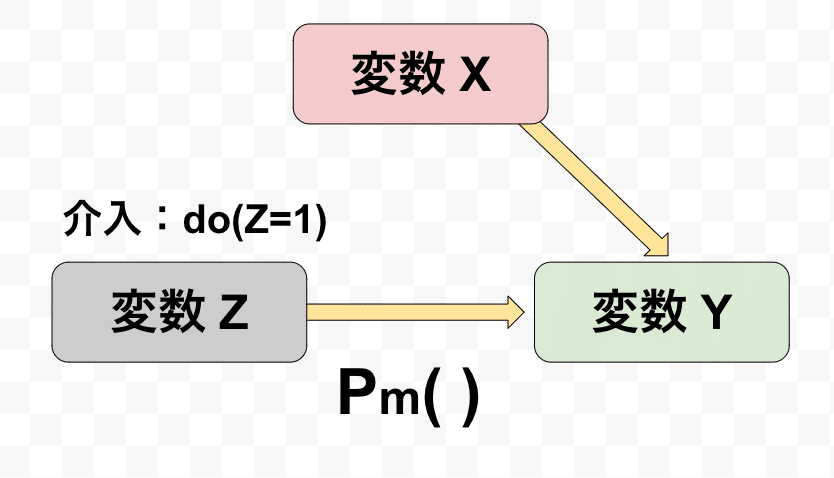
この2つの世界の間では、まず以下が成り立ちます。

$$
P(Y=y|do(Z=z)) = P_m(Y=y|Z=z)
$$

この右辺について、条件付き確率公式である、

$$
P(y|z) = \sum_x P(y|z,x) P(x|z)
$$

を利用すると、

$$
P(Y=y|Z=z) = \sum_x P_m(Y=y|Z=z,X=x) P_m(X=x|Z=z)
$$

となります。ここで、変形された$${P_m}$$において、変数$${X}$$と変数$${Z}$$には因果関係（独立）はないので、

$$
P_m(X=x|Z=z) = P_m(X=x)
$$

が成り立ち、これらを代入すると、

$$
P(Y=y|Z=z) = \sum_x P_m(Y=y|Z=z,X=x) P_m(X=x)
$$

となります。これを最初の式の右辺に置き直すと、

$$
P(Y=y \mid do(Z=z)) = \sum_x P_m(Y=y|Z=z,X=x) P_m(X=x)
$$

となります。次に、変数$${X}$$は、$${P()}$$の世界でも、$${P_m()}$$の世界でも、他からの因果のない変数であるため、

$$
P_m(X=x) = P(X=x)
$$

です。また、$${P_m(Y=y|Z=z,X=x)}$$について、変数$${Z}$$と変数$${X}$$が事前に決められた（固定された）状況における、変数$${Y}$$の確率なので、$${P_m()}$$ではなく$${P()}$$の世界で考えた場合も疑似相関は発生せず、同じと考えられるため、

$$
P_m(Y=y|Z=z,X=x) = P(Y=y|Z=z,X=x)
$$

となります。これらを代入すると、

$$
P(Y=y|do(Z=z)) = \sum_x P(Y=y|Z=z,X=x) P(X=x)
$$

となり、これを調整化公式と言います。

この調整化公式により、介入操作による確率$${P_m()}$$が、通常の確率$${P()}$$の数式で表すことができました。これによって、例えば、ATEは次のように計算できます。

$$
\begin{aligned} ATE &= E(Y_1) - E(Y_0) \\ &= E(Y_1|do(Z=1)) - E(Y_0|do(Z=0))\\ &= \sum_x E(Y|Z=1,X=x) P(X=x) - \sum_x E(Y|Z=0,X=x) P(X=x) \end{aligned}
$$

となり、これを計算すればATEが求めることができます。

具体的な計算イメージをもつために、メルマガ施策の例を考えてみましょう。変数$${X}$$である「サイトへのロイヤリティ」を仮に「低」「中」「高」の3段階とした場合、上式の左辺である

$$
\sum_x E(Y|Z=1,X=x) P(X=x)
$$

は、以下のような計算式となります。

$$
E(Y|Z=メルマガ開封,X=ロイヤリティ低) P(X=ロイヤリティ低) + E(Y|Z=メルマガ開封,X=ロイヤリティ中) P(X=ロイヤリティ中) + E(Y|Z=メルマガ開封,X=ロイヤリティ高) P(X=ロイヤリティ高)
$$

ここで例えば最初の項を見てみると、$${E(Y|Z=メルマガ開封,X=ロイヤリティ低) }$$は、【ロイヤリティが「低」かつメルマガを開封したユーザーの平均購入量】であり、$${P(X=ロイヤリティ低)}$$は【全ユーザーの中の、ロイヤリティが「低」のユーザーの割合】であり、いずれも観測値から求めることができそうですね。

同様に、右辺の$${\sum_x E(Y|Z=1,X=x) P(X=x)}$$も

$$
E(Y|Z=メルマガ未開封,X=ロイヤリティ低) P(X=ロイヤリティ低) + E(Y|Z=メルマガ未開封,X=ロイヤリティ中) P(X=ロイヤリティ中) + E(Y|Z=メルマガ未開封,X=ロイヤリティ高) P(X=ロイヤリティ高)
$$

となり、この左辺から右辺を引くことでATEを推定することが可能となります。

因果推論の実装

いよいよ、上記の因果推論の理論を、実装に落とし込んでみます。

実装の流れとしては、

  1. 因果関係を仮定した上で、ダミーのデータセットを生成する

  2. 因果推論を実装することで、因果を推定する

  3. 2の推定値が、1で仮定した因果をうまく推定できているかをチェック

のようになります。（実際の実務のシーンにおいては、データセットは観測されたデータを用いることになるため、1.のstepは不要です）

ここからは、ケーススタディ②で説明した「釣果が伸びるのは生餌？それともルアー？」をテーマに実装をおこなっていきます。このケーススタディでは、ある釣り場において、【餌タイプ（生餌 or ルアー）】が【釣果】に及ぼす影響について調べることが目的でした。

また、その際に考慮すべき変数として【性別】と【年齢】がありました。

ケーススタディ②の関連の再掲

今回は、それぞれの要素を以下のような変数に置くようにします。

  • 餌タイプが「生餌」の場合を$${Z=0}$$とし、「ルアー」の場合を$${Z=1}$$とします。

  • 釣果を$${Y}$$とします。

  • 性別を$${x_1}$$として、「男性」の場合を$${x_1=0}$$、「女性」の場合を$${x_1=1}$$とします。

  • 年齢を$${x_2}$$とします。

つまり、$${x_1}$$や$${x_2}$$の影響を考慮しながら、$${Z}$$が$${Y}$$に与える効果を因果推論していきます。

ダミーデータの生成

まずは、今回は観測データがないので、代わりとなるダミーデータを用意していきましょう。

最初に必要となるライブラリをimportします。

import random
import numpy as np

# 乱数シードの設定
np.random.seed(9999)
random.seed(9999)

from numpy.random import *
import matplotlib.pyplot as plt
import scipy.stats
from scipy.special import expit
import pandas as pd

次に、変数$${x_1}$$（性別）と変数$${x_2}$$（年齢）のデータを作っていきます。性別$${x_1}$$は0（男性）と1（女性）のランダム、年齢$${x_2}$$は20~60歳のランダムにします。

# 生成するデータ数
num_data = 400

# 性別 0(男性) or 1(女性)　のランダム
x_1 = randint(0, 2, num_data)

# 年齢　(20~60) のランダム
x_2 = randint(20, 86, num_data)

次に、変数$${Z}$$（餌タイプ）を決めます。餌タイプには以下のような傾向がありました。

  • 女性のほうが男性よりもルアーを使う傾向（$${Z^i=1}$$になる確率）が高い

  • 年齢が低くなるほどルアーを使う傾向（$${Z^i=1}$$になる確率）が高い

$${Z_i}$$を作るために、シグモイド関数 $${sigmoid(x)=\frac{1}{1+e^{-ax}}}$$ を利用して、$${Z_i=1}$$となる確率$${Z^i_{prob}}$$を次のようにします。（シグモイド関数の係数$${α}$$は1とします。）

$$
Z^i_{prob} = sigmoid[x^i_1 \times 1+x^i_2\times(-0.1)+3.5+noise^i]
$$

数式からもわかるように、女性（$${x_i=1}$$）かつ、年齢が若い（$${x_2}$$が小さい）ほど、ルアーを使う確率$${Z^i_{prob}}$$が大きくなるようになっています。

そして、この$${Z^i_{prob}}$$は0~1の値を取るので、この確率に基づいて$${Z^i}$$の値を、$${Z^i=1}$$（ルアーを使う）および$${Z^i=0}$$（生餌を使う）のいずれかに割り振っていきます。

実装は以下のようになります。

# noise
noise_z = 0.5*randn(num_data)

# シグモイド関数の入力部分を計算
# 女性の方がルアーをしやすい / 年齢が低い方がルアーをしやすい
z_base = x_1 + x_2*(-0.1) + 3.5 + noise_z

# シグモイド関数を計算
# ルアーを使用する確率　
z_prob = expit(1*z_base)


# 確率z_probにもとづいてZを決定
Z = np.array([])
for i in range(num_data):
    Z_i = np.random.choice(2, size=1, p=[1-z_prob[i], z_prob[i]])[0]
    Z = np.append(Z, Z_i)

実際に$${x_1}$$、$${x_2}$$、$${Z_{prob}}$$、$${Z}$$のデータの一部を見てみると以下のようになっています。

なんとなく、性別が女性である場合や、年代が低い場合に、ルアーを使う確率（$${Z_{prob}}$$）が高くなっていそうです。

ここまでで、$${Z_i}$$（餌タイプ）のデータが生成できたので、次に$${Y_i}$$（釣果）のデータを生成していきます。

釣果には以下のような傾向がありました。

  • 男性の方が女性よりも釣果が高くなる傾向がある

  • 年齢が高くなるほど釣果が高くなる傾向がある

また、実際に因果推論の対象である【餌タイプ】が【釣果】に与える影響としては、「生餌よりもルアーの方が釣れやすい状態」でありました。

これらを踏まえ、$${Y_i}$$のデータは以下のように生成します。

$$
Y_i = -20x^i_1 + 0.5 x^i_2 + 5Z^i + 30 + noise^i
$$

数式からもわかるように、男性（$${x_i=0}$$）の方が釣果が大きくなり、年齢が高い（$${x_2}$$が大きい）ほど釣果が大きくなり、ルアーを使っている（$${Z^i=1}$$）方が釣果が大きくなります。

ここで、$${Z^i}$$の係数は5になっているので、餌タイプの釣果への効果は+5が正解となります。

実装は以下のようになります。

e_y=randn(num_data)

Y=-20*x_1 + 0.5*x_2 + 5*Z + 30 + e_y

実際に$${x_1}$$、$${x_2}$$、$${Z}$$、$${Y}$$のデータの一部を見てみると以下のようになっています。

$${Z=0}$$（生餌を利用）のデータと、$${Z=1}$$（ルアーを利用）のデータに分けて、それぞれの要素の平均値を出してみます。

ダミーデータ生成時に工夫した通り、ルアーを利用した人の方が女性が多く、年齢が若くなっています。しかし、釣果はルアーを使った人よりも、生餌を使った人の方が高くなっています（今回は、ルアーを選んだ方が釣果が高くなるようにデータを生成したはずでした）。

このように性別や年齢による因果を考慮せず、単純な平均値で見てしまうと、「生餌の方が有利」という間違った結論を導いてしまうようなデータを生成することができました。

以上でダミーデータの準備は完了です。

線形回帰分析

ここからは、生成したダミーデータを用いて、これを観測されたデータとして、データの因果を分析していきます。

まずは単純な線形回帰を用いた因果推論を行なってみます。つまり、下式のように、$${Y^i}$$を、変数$${x^i_1}$$、$${x^i_2}$$、および$${Z^i}$$の線形回帰として表し、これらの係数である$${a}$$、$${b}$$、$${c}$$、$${d}$$を求めることで因果推論を行います。

$$
Y^i = ax^i_1 + bx^i_2 + cZ^i + d
$$

今回の事例で言えば、

$$
[釣果] = [性別が釣果に与える影響] \times [性別] + [b:年齢が釣果に与える影響] \times [年齢] + [餌タイプが釣果に与える影響] \times [餌タイプ] + [定数]
$$

となり、この中の[餌タイプが釣果に与える影響]が求めたいATE（平均処置効果）となります。

実装は、以下のように機械学習ライブラリであるscikit-learnのLinearRegressionを利用することで簡単にできます。

from sklearn.linear_model import LinearRegression

# 説明変数
X = df[["gender","age","Z"]]

# 目的変数
y = df["Y"]

# 回帰の実行
reg = LinearRegression().fit(X,y)

ここで、回帰係数を求めると以下のようになります。

つまり、回帰分析により求められた釣果$${Y^i}$$の回帰モデルは、

$$
Y^i=-20.01 \times x^i_1 + 0.50 \times x^i_2 + 5.06 \times Z^i + 30.01
$$

となり、餌タイプ$${Z^i}$$が釣果$${Y^i}$$に与える影響（つまりATE）は「+5.06」と推定されました。今回ダミーデータ生成時に利用したのは下式であり、正解は「+5」でした。

$$
Y_i = -20x^i_1 + 0.5 x^i_2 + 5Z^i + 30 + noise^i
$$

このように、単純な回帰分析によって、ほぼ正確にデータ生成時の係数を因果推論により推定することができました。

IPTW法：傾向スコアを用いた因果推論

次に、「傾向スコア」と呼ばれる指標を用いた、逆確率重み付け法（IPTW: Inverse Probability of Treatment Weighting）について見ていきます。

IPTWは、測定されたデータに対する処置を受ける確率、つまり「処置を受ける傾向」を示す指標である「傾向スコア」を用いて、因果の効果を測定する方法です。

『傾向スコアについて』
まずは傾向スコアについて説明します。前述した調整化公式を再掲します。

$$
P(Y=y|do(Z=z)) = \sum_x P(Y=y|Z=z,X=x) P(X=x)
$$

この調整化公式の右辺は、$${\sum_x}$$の中で、$${P(Y=y|Z=z,X=x)とP(X=x)}$$の掛け算になっており、変数Xが取りうる全ての数のペアの全組み合わせを計算するのはコストが高くなります。そこで、同時確率式の$${P(a,b) = P(a|b)P(b)}$$を利用することで、

$$
P(Y=y|Z=z,X=x) = \frac{P(Y=y,Z=z,X=x)}{P(Z=z|X=x)}
$$

のように変形でき、これを用いて調整化公式を整理すると、

$$
P(Y=y|do(Z=z)) = \sum_x \frac{P(Y=y,Z=z,X=x)}{P(Z=z|X=x)} = \sum_x \frac{P(x,y,z)}{P(z|x)}
$$

となり、変数$${X}$$の組み合わせの掛け算を無くすことができました。
分子の$${P(x,y,z)}$$は観測データのサンプルサイズから簡単に求めることができます。

一方、分母の$${P(z|x)}$$は、変数$${X=x}$$のもとで、変数$${Z=z}$$となる確率であり、これを「傾向スコア」といいます。

傾向スコア$${P(z|x)}$$を求める確率式としてロジスティック回帰を利用します。

ロジスティック回帰はシグモイド関数を使って、連続値の入力から確率値（0~1）を出力するものであり、もともと今回のダミーデータ生成の際にも、以下のようなシグモイド関数を利用していましたね。

$$
Z^i_{prob} = sigmoid[x^i_1 \times 1+x^i_2\times(-0.1)+3.5+noise^i]
$$

つまり、傾向スコアを求めるということは、観測データ（今回は生成したダミーデータ）に対して、ロジスティック回帰を利用して、

$$
Z^i_{prob} = sigmoid[\beta_1x^i_1 + \beta_2x^i_2 + \alpha ]
$$

の各係数$${\beta_1}$$、$${\beta_2}$$、$${\alpha}$$を求めることになります。

傾向スコアを求める実装コードは以下のようになります。ロジスティック回帰にはscikit-learnのLogisticRegressionを利用します。

from sklearn.linear_model import LogisticRegression

# 説明変数
X = df[["gender", "age"]]

# 目的変数
Z = df["Z"]

# 回帰の実施
reg = LogisticRegression().fit(X,Z)

# 傾向スコアを推測
Z_pre = reg.predict_proba(X)

回帰によって算出された各係数は以下のようになりました。

結果は$${\beta_1=1.01}$$、$${\beta_2=0.08}$$、$${\alpha=2.66}$$となっていて、正解である、$${\beta_1=1}$$、$${\beta_2=0.1}$$、$${\alpha=3}$$と比べて、いずれも近い数字になりました。

『IPTW法による因果推論』

次に、上で求めた傾向スコアを用いてATEを求めていきましょう。ATEの計算式は、

$$
\begin{aligned}ATE &= E(Y_1) - E(Y_0) \\&= E(Y_1|do(Z=1)) - E(Y_0|do(Z=0)) \\&= \sum_x E(Y|Z=1,X=x) P(X=x) - \sum_x E(Y|Z=0,X=x) P(X=x)\end{aligned}
$$

であり、傾向スコアの説明のところの式変形を用いると

$$
\begin{aligned} ATE = \sum_x \frac{P(Y=y,Z=1,X=x)}{P(Z=1|X=x)} P(X=x) - \sum_x \frac{P(Y=y,Z=0,X=x)}{P(Z=0|X=x)} P(X=x) \end{aligned}
$$

となります。そして、$${Y}$$が離散値ではなく連続値の場合は、下記のようになります。

$$
ATE = \frac{1}{N} \sum_i^N \frac{y_i}{P(Z=1|X=x_i)}Z_i - \frac{1}{N}\sum_i^N \frac{y_i}{P(Z=0|X=x_i)}(1-Z_i)
$$

実装コードは以下のようになります。

ATE_i = Y/Z_pre[:, 1]*Z - Y/Z_pre[:, 0]*(1-Z)
ATE = 1/len(Y)*ATE_i.sum()

実際にIPTW法によるATEを計算すると以下ように「6.40」となりました。

今回、ダミーデータ生成時に利用した餌タイプ（$${Z}$$）の釣果（$${Y}$$）に対する影響は「+5」であったので、IPTW法による傾向スコアを用いた因果推論でも、まずまず正確なATEを推測することができました。

DR法：反実仮想を考慮した因果推論

最後に、DR法（Doubly Robust Estimation）という因果推論の手法を見ていきます。

一つ前のIPTW法のATEの計算式を以下に再掲します。

$$
ATE = \frac{1}{N} \sum_i^N \frac{y_i}{P(Z=1|X=x_i)}Z_i - \frac{1}{N}\sum_i^N \frac{y_i}{P(Z=0|X=x_i)}(1-Z_i)
$$

ここで、$${Z_i}$$は0か1であり、$${Z_i=0}$$の場合は前半の項、$${Z_i=1}$$の場合は後半の項が0となるため、いずれの場合も、どちらか一方の項しか使われないことになります。

そこで、回帰分析を使って、反実仮想である$${Y_1^i}$$の推定値$${\hat Y_1^i}$$を計算し、この推定値をIPTW法と組み合わせます。

具体的には、とある$${i}$$さんの処置効果の前半の項を

$$
\frac{y_i}{P(Z=1|X=x_i)}Z_i
$$

から、

$$
\frac{y_i}{P(Z=1|X=x_i)}Z_i + \bigg( 1 - \frac{Z_i}{P(Z=1|X=x_i)} \bigg) \hat Y_1^i
$$

に置き換えることで、$${Z_i=0}$$の時に$${\hat Y_1^i}$$となり、反実仮想である$${E(Y_1|do(Z=1))}$$の値が$${\hat Y_1^i}$$となります。同様に後半の項も、

$$
\frac{y_i}{P(Z=0|X=x_i)}(1-Z_i)
$$

から、

$$
\frac{y_i}{P(Z=0|X=x_i)}(1-Z_i) + \bigg( 1 - \frac{1-Z_i}{P(Z=0|X=x_i)} \bigg) \hat Y_0^i
$$

に置き換えることで、$${Z_i=1}$$の時に$${\hat Y_0^i}$$となり、反実仮想である$${E(Y_0|do(Z=0))}$$の値が$${\hat Y_0^i}$$となります。

こうすることで、IPTW法では考慮できてなかった各人の反実仮想を計算に含めることができます。

最終的なATEの計算式は以下のようになります。

$$
ATE = \frac{1}{N} \sum_i^N \bigg\{ \bigg( \frac{y_i}{P(Z=1|X=x_i)}Z_i + \big( 1 - \frac{Z_i}{P(Z=1|X=x_i)} \big) \hat Y_1^i \bigg) - \bigg( \frac{y_i}{P(Z=0|X=x_i)}(1-Z_i) + \big( 1 - \frac{1-Z_i}{P(Z=0|X=x_i)} \big) \hat Y_0^i \bigg) \bigg\}
$$

実装は以下のようになります。

はじめに線形回帰モデルを構築し、それを用いて、$${\hat Y_1^i}$$および$${\hat Y_0^i}$$を計算します。

# 説明変数
X = df[["gender", "age", "Z"]]

# 目的変数
y = df["Y"]

# 回帰の実施
reg = LinearRegression().fit(X, y)

# Z=0の場合
X_0 = X.copy()
X_0["Z"] = 0
Y_0 = reg.predict(X_0)

# Z=1の場合
X_1 = X.copy()
X_1["Z"] = 1
Y_1 = reg.predict(X_1)

次に、傾向スコアは、先述のIPTW法の際と同じ方法で以下のように求めます。

from sklearn.linear_model import LogisticRegression

# 説明変数
X = df[["gender", "age"]]

# 目的変数
Z = df["Z"]

# 回帰の実施
reg_pre = LogisticRegression().fit(X,Z)

# 傾向スコアを推測
Z_pre = reg_pre.predict_proba(X)

最後にATEを計算します。DR法でのATEは以下のような式で計算できるのでしたね。

$$
ATE = \frac{1}{N} \sum_i^N \bigg\{ \bigg( \frac{y_i}{P(Z=1|X=x_i)}Z_i + \big( 1 - \frac{Z_i}{P(Z=1|X=x_i)} \big) \hat Y_1^i \bigg) - \bigg( \frac{y_i}{P(Z=0|X=x_i)}(1-Z_i) + \big( 1 - \frac{1-Z_i}{P(Z=0|X=x_i)} \big) \hat Y_0^i \bigg) \bigg\}
$$

この式をそのまま実装に落とし込むと下記のようになります。

ATE_1_i = Y/Z_pre[:, 1]*Z + (1-Z/Z_pre[:, 1])*Y_1
ATE_0_i = Y/Z_pre[:, 0]*(1-Z) + (1-(1-Z)/Z_pre[:, 0])*Y_0

ATE = 1/len(Y)*(ATE_1_i-ATE_0_i).sum()

実際にDR法によるATEを計算すると以下ように「5.11」となりました。

今回、ダミーデータ生成時に利用した餌タイプ（$${Z}$$）の釣果（$${Y}$$）に対する影響は「+5」であったので、DR法によってかなり正解に近いATEを推測することができました。

IPTW法によるATEの推測は「6.4」であり、IPTW法に「反実仮想の考慮」という一手間を加えたDR法を用いることで、因果推論の精度を高めることができたことになります。

まとめ

今回は、因果推論の入門的な内容についてまとめました。

具体的には、架空のケーススタディ（例えば「メルマガ施策」や「餌タイプと釣果」）を用いて、

  • 因果推論の必要性

  • 相関と因果の違い、疑似相関

  • 介入、調整化公式、傾向スコア

  • 線形回帰、IPTW法、DR法

などについて解説しました。

また、「餌タイプと釣果」の因果推論では、線形回帰やDR法による平均処置効果（ATE）の推定でかなり良い結果を得ました。

しかし、皆さんの中には「本当にこんな単純な手法で効果を正確に因果推論できるのか？」という疑問を持つ方もいるかもしれません。その疑問は正当であり、現実のデータや状況では、今回紹介したようなシンプルな手法で正確な因果推論を行うことは稀です。

具体的には、今回のケーススタディで用いたダミーデータは、以下のような前提に基づいていました。

  • $${Y}$$（釣果）が$${X}$$（性別、年齢）や$${Z}$$（餌タイプ）の線形回帰で表現できる。

  • 傾向スコア$${P(Z|X)}$$がロジスティック回帰でモデル化できる。

  • $${X}$$（性別、年齢）による$${Z}$$（餌タイプ）の$${Y}$$（釣果）への影響は一定である。（例えば、「年齢が高くなるにつれてルアーの釣果への影響が減少する」といった変化はない）

しかし、実際のデータはより複雑で、これらの前提が成立しない場合が多く、因果推論にはより高度な手法が必要になります。

ただし、そのような発展的な因果推論手法を理解・使用するためにも、今回紹介した基礎知識が重要です。

次回、続編を書く機会があれば、より実践的な制約を伴う因果推論の手法や実装、さらにはANGLERSでの因果推論の実際の事例について詳しく解説したいと思います。

最後までお読みいただきありがとうございました。

エンジニアの方でアングラーズにご興味のある方は、ぜひ気軽にご連絡ください。

この記事が気に入ったらサポートをしてみませんか？