[PYTHONで制御設計]スイッチングレギュレータ(降圧DCDC)の位相補償設計

今回は電流制御モード降圧DCDC(スイッチングレギュレータ)のコントローラーの設計をPYTHON controlを使って行ったので、その具体的内容を詳細解説します。

制御設計理解の一助となれば、幸いです。

前回はプラントの伝達関数をpython controlを使って解析しました。良かったら見てみてください。

この記事を読むとわかること

①電流モード降圧スイッチングレギュレータの制御設計の具体的手順

②制御設計から位相補償の定数値に落とし込む具体的手順

③それらがPYTHONで実現する方法

それではやってみましょう。

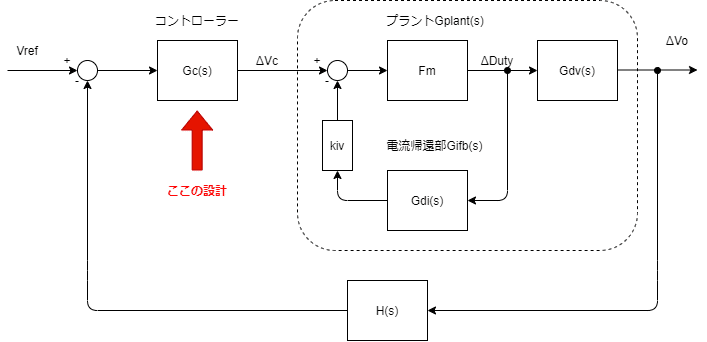
系全体のブロック線図はこれ

前回は点線で囲んだプラントの伝達関数を解いて、解析してました。

今回は以下のコントローラーブロックGc(s)を設計していきます。

コントローラー設計、位相補償設計の目標

コントローラーの目標はスイッチングレギュレータを安定して動かすことです。

安定性に関しては過去に以下記事を書いておりますので、こちらも良かったら見てみてください。

安定性は位相余裕度とゲイン余裕度で測ることができます。

目安としては位相余裕度：45deg以上、ゲイン余裕度：7dB以上で実用上問題ありません。

今回もこの目標で設計してみたいと思います。

コントローラー設計の発想・考え方

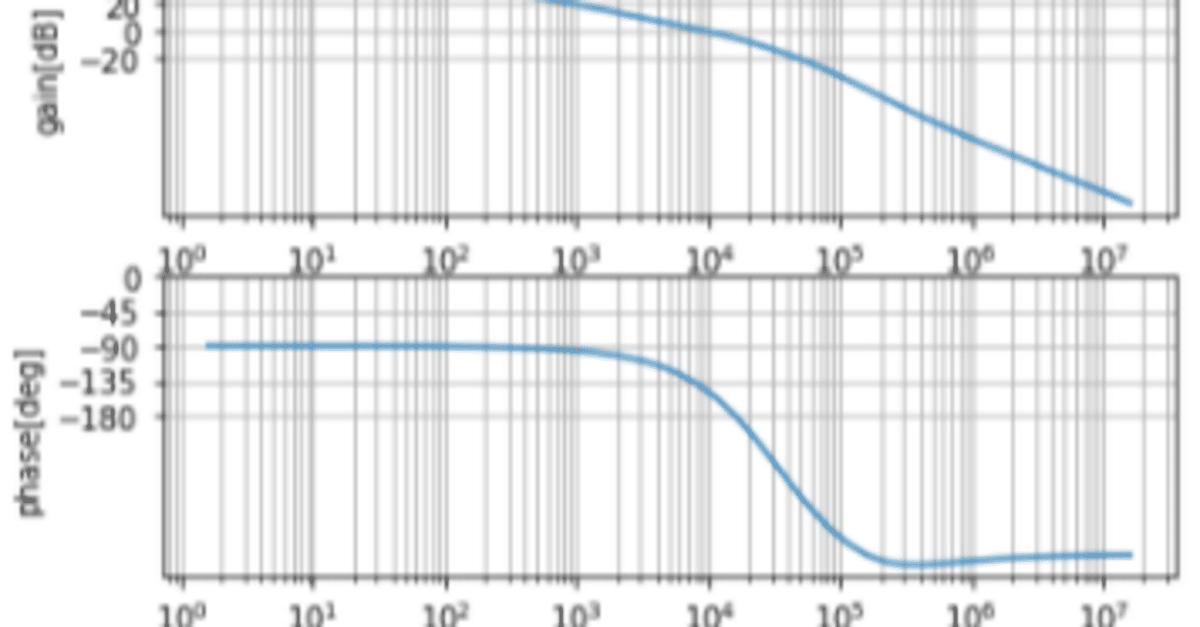
電流制御モードスイッチングレギュレータのプラント伝達関数はこんな感じになります。これは前回の記事で解いていますので、割愛させて頂き結果だけ示します。

ポイントは低周波数領域に1個ポール(位相遅れ)があって、そのあとに高周波数領域にポールやPWMの無駄時間の影響で位相がぐわーっと回っています。

コントローラーの発想としては、

「最初っからポールがおって、プラントの低域のポールにゼロ点(位相進み)をぶち当てたら、ゲインは一直線20dB/decになるから設計しやすいじゃん。」

「高域のわちゃわちゃしたところはポールを入れといて、ゲインを落として悪さしないようにしとけばいいじゃん。」

です。

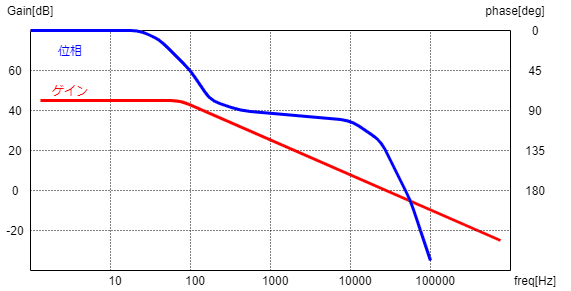
なので、コントローラーの周波数特性は以下のような感じのものを使います。

最初のゼロ点(位相進み)をプラントのポール(位相遅れ)と同じ周波数に設定します。

高域(クロスオーバー周波数より十分に大きい周波数)にポール(位相遅れ)を入れておいて、高域のゲインをしっかり落としておく。

クロスオーバー周波数：ゲインが0dBと交差する周波数

というのが基本的な設計の考え方になります。

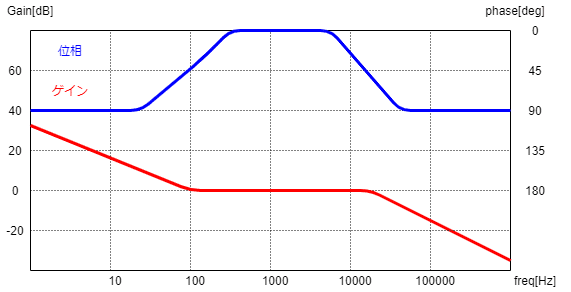
そうするとざっくり目標となる周波数特性は以下のようになるイメージです。

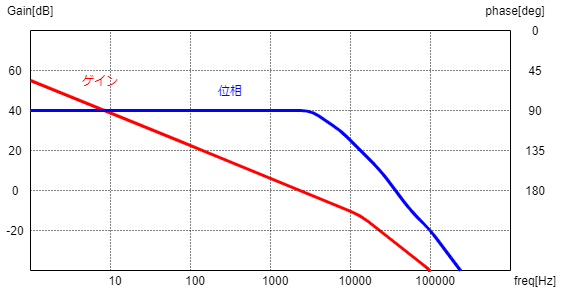
プラントのポールはコントローラーのゼロと打消しあって、ゲインは一直線20dB/decで落ちていきます。

位相は90deg回った状態でキープされて、無駄時間もしくはコントローラーのポールで落ちていきます。

こうすることにより、出力電圧が変動した時の反応速度の指標となるクロスオーバー周波数を決めたら、自動的に20dB/decで辿っていけば、DCゲインが決まります。

DCゲイン値やクロスオーバー周波数やゼロ点周波数から位相補償の抵抗値やコンデンサ容量値を計算していくという流れになります。

回路構成と伝達関数と設計手順

では上記のコントローラーを実現する回路はどんなのか？そしてコントローラーの伝達関数はどんななのか？を示します。

電流モード制御の降圧スイッチングレギュレータのコントローラーの回路構成は以下の通りです。

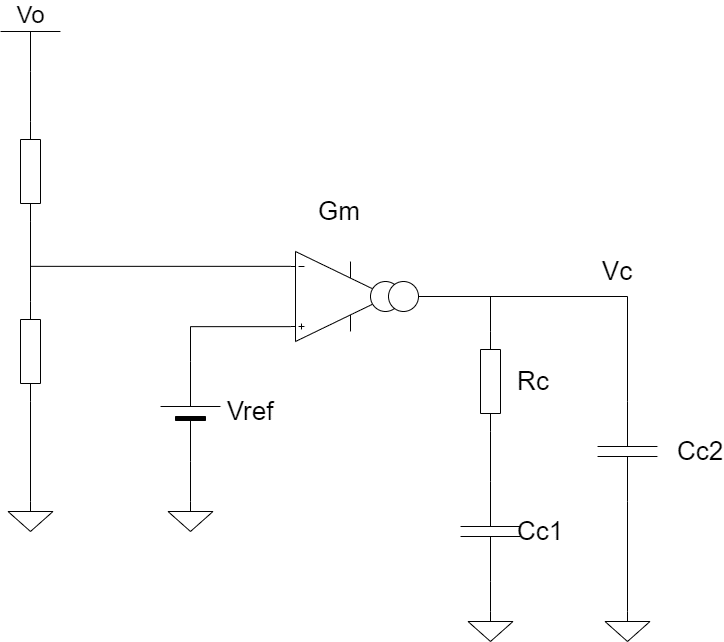
この回路ブロックの伝達関数は以下の通りになります。導出過程をやると大変なので、最初はこうなると思っておけば問題ないと思います。

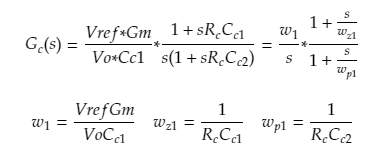
Vref：基準電圧、Gm：エラーアンプトランスコンダクタンス、Vo：出力電圧

あとは設計手順ですが、

①ωz1のゼロ点(位相進み)をプラントのポール(位相遅れ)と同じ周波数に設定

②所望のクロスオーバー周波数になるようにDCゲイン(≒ω1)を設定

③クロスオーバー周波数より十分高域にポールωp1を設定(fbw*10倍以上が目安)

で終了です。そのあとwz1,wp1,w1が決定したら、以下の式に変形して回路定数を設定すれば、設計終了です。

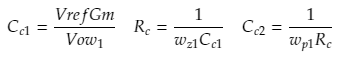
pythonでの実現方法

前提の話は以上として、コントローラー設計のプログラムを示します。

やっていることは

条件決めて
↓
プラントの伝達関数とボード線図解いて
↓
先ほどの設計思想に基づいてコントローラーのゼロ点、ポールを配置
↓
系全体のボード線図示す。

という流れです。

#import
import numpy as np
import matplotlib.pyplot as plt
import sympy as sym
import control as ctl

#外部条件の設定
Vi_max = 16#入力電圧最大値[V]
Vi_typ = 12#入力電圧[V]
Vi_min = 8#入力電圧最小値[V]
Vo = 5#出力電圧[V]
f_pwm = 100*10**3#スイッチング周波数[Hz]
Ts = 1/f_pwm#周期[sec]
Io_max = 2#出力電流最大値[A]
Io_typ = 1#出力電流typcal値[A]
Io_min = 0.1#出力電流最小値[A]

#コイル値の候補を計算
d_IL = Io_min * 2
L_vimax = (Vi_max - Vo)/d_IL * Vo / (Vi_max * f_pwm)
L_vityp = (Vi_typ - Vo)/d_IL * Vo / (Vi_typ * f_pwm)
L_vimin = (Vi_min - Vo)/d_IL * Vo / (Vi_min * f_pwm)

#インダクタンス値を決定する。
L_pre = max(L_vimax,L_vityp,L_vimin)#計算値で最大のものを選ぶ

#自分で入力するセル。インダクタンス値を決定する。
L = 150 * 10**(-6)#L_preに近い実在する値を選択する。
r_L = 0.03#コイルのDCR[Ω]

#リップル電流
Iripple_min = (Vi_min-Vo)/L * Vo/Vi_min * Ts
Iripple_typ = (Vi_typ-Vo)/L * Vo/Vi_typ * Ts
Iripple_max = (Vi_max-Vo)/L * Vo/Vi_max * Ts

#リップル電流とリップル電圧の確認
#Iripple_min,Iripple_typ,Iripple_max

#出力コンデンサの値を計算
Vripple_target = 0.1#出力リップル電圧[V]の狙い値を記入する。
r_C = 0.1#出力コンデンサのESR値[Ω]
C_pre = 1/(8*f_pwm*(Vripple_target/Iripple_max - r_C))
#C_pre

#出力コンデンサの容量値を決定する
C = 47 * 10**(-6)
r_C = 0.01#コンデンサのESR[Ω]

Vripple_max = Iripple_max * (r_C + 1/(8*f_pwm*C))
#Vripple_max

#伝達関数計算
Kiv = 0.1#電流帰還率[Ω]
Sn = ((Vi_typ-Vo)/L)*Kiv#電流帰還のスロープ波形の傾き
Fm = 1/Sn/Ts#スロープ部の伝達関数

#######################################################################
#プラントの伝達関数を計算
tf_Fm = ctl.tf([Fm],[1])
tf_Kiv = ctl.tf([Kiv],[1])
tf_Gdi = ctl.tf([C*Vi_typ,0],[C*L,2*C*((r_C+r_L)/2),1])
tf_Gdv = ctl.tf([Vi_typ*C*r_C, Vi_typ],[C*L,2*C*((r_C+r_L)/2),1])
tf_ifeedback = ctl.series(tf_Kiv, tf_Gdi)
tf_plant_pre = ctl.feedback(tf_Fm,tf_ifeedback)
tf_plant = ctl.series(tf_plant_pre, tf_Gdv)
#無駄時間の伝達関数
num_delay, den_delay = ctl.pade(Ts, 1)
#プラント+むだ時間の伝達関数
Gplant = tf_plant * ctl.tf(num_delay, den_delay)

#プラントのボード線図の計算
gain_plant, phase_plant, w = ctl.bode(Gplant, Plot=False)
f = w/2/np.pi#単位を[rad/sec]を[Hz]に変換
gain_plant_dB = 20*np.log10(gain_plant)#単位を[dB]に変換
phase_plant_deg = phase_plant * 180/np.pi#単位を[rad]から[deg]に変換

#plantのボード線図表示
fig, ax = plt.subplots(2,1)
ax[0].semilogx(f, gain_plant_dB)
ax[0].set_yticks([-20,0,20,40,60])
ax[0].grid(which = "both", axis = "x")
ax[0].grid(which = "both", axis = "y")
ax[0].set_ylabel("gain[dB]")
ax[1].semilogx(f, phase_plant_deg)
ax[1].set_yticks([-180,-135,-90,-45,0])
ax[1].grid(which = "both", axis = "x")
ax[1].grid(which = "both", axis = "y")
ax[1].set_ylabel("phase[deg]")
ax[1].set_xlabel("f[Hz]")

#######################################################################

#フィードバック部分の伝達関数
Vref = 1#基準電圧
H = ctl.tf([Vref/Vo],[1])

#######################################################################
#コントローラー部分の伝達関数
Gm = 1000 * 10**(-6)#エラーアンプトランスコンダクタンス[S]
pole = ctl.pole(Gplant)/2/np.pi#プラントの極を計算
f_p1_plant = min(np.abs(pole))#プラントのfirst pole周波数[Hz]
fbw = 10 * 10**3#目標クロスオーバー周波数[Hz]
K = 2*np.pi*fbw*C*Kiv#補償器(コントローラー)の利得
f1 = f_p1_plant * K#補償器(コントローラー)のゼロクロス周波数[Hz]
w1 = 2*np.pi*f1#f1をradに変換
wz = 2*np.pi*f_p1_plant#プラントのポールと補償器のゼロ点を合わせる。
fp1 = 10 * fbw
wp1 = 2*np.pi*fp1
Cc1 = Vref/Vo*Gm/w1
Rc = 1/wz/Cc1
Cc2 = 1/wp1/Rc

Z = ctl.tf([Rc*Cc1,1],[Rc*Cc2,1,0])
tf_erroramp = ctl.tf([Gm/Cc1],[1])
tf_H_eamp = ctl.series(H,tf_erroramp)
Gerror = ctl.series(tf_H_eamp,Z)

gain_ctl, phase_ctl, w = ctl.bode(Gerror, Plot=False)
f = w/2/np.pi#rad/secをHzに変換
gain_ctl_dB = 20*np.log10(gain_ctl)#dBに変換
phase_ctl_deg = phase_ctl * 180/np.pi#radをdegに変換

#######################################################################
#コントローラーのボード線図表示
fig, ax = plt.subplots(2,1)
ax[0].semilogx(f, gain_ctl_dB)
ax[0].set_yticks([-20,0,20,40,60])
ax[0].grid(which = "both", axis = "x")
ax[0].grid(which = "both", axis = "y")
ax[0].set_ylabel("gain[dB]")
ax[1].semilogx(f, phase_ctl_deg)
ax[1].set_yticks([-180,-135,-90,-45,0])
ax[1].grid(which = "both", axis = "x")
ax[1].grid(which = "both", axis = "y")
ax[1].set_ylabel("phase[deg]")
ax[1].set_xlabel("f[Hz]")

#######################################################################
#系全体の伝達関数
Gtotal = ctl.series(Gerror, Gplant)

gain, phase, w = ctl.bode(Gtotal, Plot=False)
f = w/2/np.pi#rad/secをHzに変換
gain_dB = 20*np.log10(gain)#dBに変換
phase_deg = phase * 180/np.pi#radをdegに変換


#系全体のボード線図表示
fig, ax = plt.subplots(2,1)
ax[0].semilogx(f, gain_dB)
ax[0].set_yticks([-20,0,20,40,60])
ax[0].grid(which = "both", axis = "x")
ax[0].grid(which = "both", axis = "y")
ax[0].set_ylabel("gain[dB]")
ax[1].semilogx(f, phase_deg)
ax[1].set_yticks([-180,-135,-90,-45,0])
ax[1].grid(which = "both", axis = "x")
ax[1].grid(which = "both", axis = "y")
ax[1].set_ylabel("phase[deg]")
ax[1].set_xlabel("f[Hz]")

#######################################################################
#位相余裕度、ゲイン余裕度とかの計算
gm,pm,wpc,wgc = ctl.margin(Gtotal)

gm,pm,wgc/2/np.pi

そして得られる系全体のボード線図が以下の通りです。

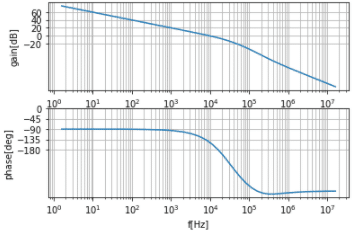
プログラムの最後にゲイン余裕度、位相余裕度、クロスオーバー周波数を表示しました。

安定度は結構ギリギリ、、、アウトって感じですね。もうちょっと調整してちゃんと位相余裕度、ゲイン余裕度がしっかりとれる領域に設定したほうがいいです。

でもまぁこれはね。計算できるようにするっていうのが大きいですから。

まとめ

長くなりましたが、まとめます。今回は電流モード制御のスイッチングレギュレータの制御設計をpythonを使って実現してみました。

制御設計で大事な考え方は

・プラント(制御対象)の最初のポールにコントローラーのゼロを同一周波数にすることでプラントの位相遅れを打ち消して、系全体のゲインを-20dB/decの一直線にする。

・所望のクロスオーバー周波数が得られるDCゲインを設定する。

・高域の位相回りしだす前にゲインを落とすようにコントローラーのポールで落としておく。

です。

以上です。かなり長い内容になりましたが、最後までお読みいただきありがとうございました！！

何かの参考になれば、幸いです！！！