[デジカ] マリガン導入後初期手札でLv.3が引ける確率

2023年3月27日 21:53

■序

2023年5月1日(月)よりデジモンカードにマリガンが導入される。
本記事では、マリガン導入後Lv.3を初期手札に引ける確率を掲載する。
また、マリガン実装前後の初期手札の計算方法が難しく悩んでいたプレイヤーもいるかもしれない。
なるべく簡単に求められる工夫した計算式も示しておく。
デジモンカードゲームをマリガン導入前から楽しんでいる既存プレイヤー、これから始める新規プレイヤーともにこの情報がデッキ構築採用枠の一つの指針として役に立てば幸いである。

[付録1], [付録2]は本記事で主として取り扱う内容ではないため、興味がある読者以外は読み飛ばして構わない。([付録2]2023年3月27日未掲載。後ほど更新予定)

■マリガン実装の影響

デジモンカードゲームにおいて、マリガン導入前後で最も変化することはLv.3の枚数と考えている。
デッキの構築タイプによって影響の差はあるため本記事では典型的な順当進化型に焦点を当てる。
現在のルールでは、１発で初期手札にLv.3を引くことがプレイヤーの大きな課題の一つであった。
その課題に取り組むためLv.3の枚数を重視し14から16枚ほど採用枠を割き、初動の事故を防止していた。

一方でテイマー、オプション、高Lvデジモンの採用枠が少なくなるため、セキュリティのパワーも下がってしまうという負の一面も生まれてしまう。
マリガン導入後では、Lv.3を初期手札に引ける確率が上がるためLv.3の採用枠を減らし、他の枠に当てることでセキュリティのパワーを上げることも進化事故の発生も下げることができる。

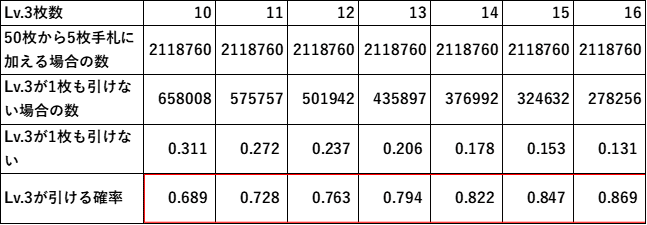
■マリガン導入前後による初期手札にLv.3が1枚以上引ける確率

今回算出した計算方法の詳細は後で述べ、先に確率の結果と変化量について記載する。結果は小数点第４位で四捨五入した値である。

上記の結果より、10枚でも約90%の確率で初期手札事故は回避できるということが判明した。
ワンショットのデッキではLv.3を絞ってサーチカードを多めに採用することで再現性が高くなると推測している。
12枚が約94%で、同No.カードを4枚まで採用可能なデジモンカードとしては非常にバランスが良い状態であり、約20回に１回程度の事故であればスイスドロー予選5回、決勝トーナメント本選3回の大会でも安心して構築できる枚数である。

■算出した計算方法

●マリガン導入前の初期手札を引くまでの手順

山札50枚からセキュリティに5枚置く。(セキュリティの内容は確認しない)
山札45枚から手札として5枚引く。

セキュリティの内容が非公開の状態で山札から手札として5枚引くため、この確率は最初に山札50枚から手札として5枚引いてLv.3が引ける確率と一致する。そのため、余事象を用いて次のように求めることができる。

1-(手札にLv.3が０枚の確率)

非公開とはいえセキュリティにLv.3が埋まるため、埋まる枚数によって確率が変動するのではないかと疑問をもつ読者もいると思う。
中学数学で学習した元に戻さないくじの「くじの公平性」についての問題を参考にしながら考えれば腑に落ちやすいかもしれないが、実際の問題は複雑であり本当に大丈夫なのかと不安になる気持ちは十分に理解できる。
[付録1]では別計算として各場合に分けて計算した方法も後で記載するため、そちらを参考にしてほしい。
また今回の算出結果が偶然の一致ではないかと懐疑的になってしまうことも重々承知している。
[付録2]では順序にかかわらず確率が等しいことを証明しておく。興味のある読者のみ参考にしていただきたい。また、計算に間違いがあった場合はぜひとも教えていただきたい。

●マリガン導入後の初期手札を引くまでの手順

山札50枚から手札として5枚引く。(内容を確認する)
マリガン申請後再度山札から5枚引く。

最初の確認で手札にLv.3が引くことができれば操作を終了し、引けなかったときはマリガンを行いLv.3を引ける確率を考える。

したがって、余事象を用いて次のように求める。

1-(1回目にLv.3が引けない確率)×(2回目にLv.3が引けない確率)

■最後に

今回は2023年5月1日(月)以降マリガン実装後の初期手札でLv.3が引ける確率を掲載させていただいた。
デッキタイプによっては、例えばベルゼブモンのようにLv.3を16枚入れたほうが強いデッキもあるため、この数値は全ての順当進化型がLv.3を削った方がよいという結果にはなっていない。
また、2023年5月下旬にはAce記述を持つ低コスト高Lvのデジモンも扱えるため、Lv.3が必ずしも初期手札に必要であるという環境ではなく、Lv.3の枚数を減らした構築が優秀な状態になっているかもしれない。
ただ、Lv.3が10枚でも90％の確率で初期手札で引けるという事実は今までのマリガン導入前の環境よりもより一層質の高い対戦が出来て、対戦終了後の感想戦なども意義のあるものになると考えられる。
今現在楽しんでいる既存プレイヤーもこれから始める新規プレイヤーもデジモンもしくはデジモンカードが好きで取り組んでいる方が大半だと思っているため、一丸となって盛り上げていきたい。
この結果はLv.3のデジモンを1枚以上引くという点を重視したため、Lv.4以降のデジモンが引けないという事故は考慮していないのが不十分な点だと感じており今後課題である。
また、今回紹介した計算式はマリガン導入後ではセキュリティに対象のカードが埋まる計算にも応用ができる。
ベルスターモンのデッキタイプであれば手札を確認して、セキュリティにオプションが埋まる確率を事前に算出することで順当進化型以外のデッキ構築も変わる可能性がある。

氷雨くん(@Hisa_Meluga)は今回の計算調査の立案者である。感覚的には明らかに確率は上昇するという事実に留まらず、そこからデッキ構築が変わるのではないかという問題提起をいただいた。
10枚でも初期手札の事故は起きにくいため、オプションやテイマーに割いてセキュリティのパワーを上げること、サーチカードを増やして進化の再現性を高めることが可能になることが数値上考えられる。
また、計算の大半はすでに氷雨くんによって計算されていたため実績は彼にある。
私は計算しやすい方法を提案させていただいた。
もし計算に間違いがある場合は私の方で修正した内容であるため、非は私の方にある。ぜひとも指摘していただきたい。

■付録1(マリガン導入前の別計算)

ここではセキュリティにLv.3が埋まった各枚数で場合分けをして算出して最後に合計して算出した方法の結果を記載しておく。

A＝(セキュリティにLv.3がk枚埋まっている場合の数)/(50枚から5枚手札に加える場合の数),
B=(セキュリティにLv.3がk枚埋まっているときに手札にLv.3が1枚も引けない場合の数)/(セキュリティに5枚置いた後に手札を5枚引く場合の数)

とする。

(セキュリティにLv.3がk枚埋まっているときに手札にLv.3が1枚も引けない確率)=A×Bで算出した。

■付録2(順序にかかわらず確率が等しいことの証明)

メモ書き
山札n枚、セキュリティ,手札r枚、Lv.3の枚数k枚

はじめにn枚の山札から手札にr枚引いてLv.3が引けない事象をA、山札n枚から中身を確認せずにセキュリティにr枚置き、その後n-r枚の山札から手札にr枚引いてLv.3が引けない事象をBとする。ただし、n, k, rは、n>k+r, k>r,r≧0を満たす非負の整数とする。

P(A)=(n-k)Cr / nCr
P(B)=Σ_[i=0]^[r] ( (kCi)*( (n-k)C(r-i) ) / nCr ) * ( ( (n-r-k+i)Cr ) / (n-r)Cr )
ヴァンデルモンドの畳み込みを利用することでP(A)=P(B)が示せる。