力学の超基礎を令和２年環境計量士過去問（環物問10）でやってみる（そにょ3　博士が愛した数式）

長々と円運動の話をやっているようですが、終わりたくても終われない、すでに喉が渇いてきている感じです。

さて、前回弧度法まで導入して少し怪しい愛じゃなくてi（虚数）を導入してみたのですが、こいつをなぜ使うのかというと、簡単に言えば回転考える時楽ができるからです。行列で一次変換とか学んでいたらいいのですが、確かいま大学だったような。大数学者として高名なガウス先生がこんな平面を考えています。前回と同じ図ですね。

x軸のところに実数、y軸に虚数を取っています。これの便利なのは、正直あまりきちんと理解できていなくてもあたかも普通の数式みたいに掛け算やったり微積やったりできるし使いでいいのです。

さて、円運動、今回は等速円運動に絞ってみますが、高校でこんな感じで習ってわかんねーと思いながら早弁した思い出があるかもしれません。

速度：
向きは円の接線
微小時間Δtの間の長さは、弧の長さとほぼ一緒なのでΔx=rωΔt
よって速さ　v=Δx/Δt=rω
加速度：
向きは、怪しい図から中心向き
速度変化の大きさは図の⇒の長さと一緒なので速さがrωなのに着目して
加速度の大きさ　a=Δv/Δt = rω^2
さっきのはやさの答えをωの式に直すとω=v/rなのでみんな大好き円運動加速度の大きさの公式a = v^2/rがでてきます。

さて、これわすれた、お絵描きもよーでけへんしぴーんちって時に、速度の定義が変位の微分、加速度が速度の微分（変位の2回微分）ってのを使って無理やり解いちゃうこともできます。

この時、点Pの場所（変位）を普通に最初の場所α、時間t、角速度ωとおくと、座標で書いたらPは(cos(θ), sin(θ))、θ=α+ωtになります。めんどくさいので、αは0にでもしましょうか。Pは (cos(ωt), sin(ωt))これは三角関数の定義のひとつですね。

さて、回転考える時ここで複素数iの出番です。この時のPの変位をxとして複素数で書くと
x = r cos ωt + i r sin ωt
ここから、微分してもそんなにしんどくないですが、さらにここでオイラーさんの定義でも使います。「博士の愛した数式」を読まれたまたは映画でご覧になられた方も多いかと思います。こんな式です。これ、証明には少なくともマクローリン展開とかが必要でかなりきっちりした議論もいるものですが私には理解できません。しかし便利なのでゴリゴリ結果は使います。

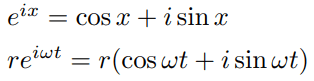
この数式、左側微分するのはものすごく楽で、機械的にやるだけで速度と加速度の公式が出てきます。あ、これ練習問題にしときますのでやってみてください。（練習問題そにょ１：上の式のうち、下の方をtについて左側の式つかって1回微分してvを、2回微分してaをだしましょう。また、その答えから右側のような「なんとか×cos x + i sin x」の形を出してみましょう。ただし、eは自然対数の底とし、e^axをxで1回微分するとa*e^axになることに注意。）

なお、ここでもういっこ面白いのは、速度は1回微分の形になるのでiだけかけた形になります。実は、虚数平面でiを１回かけると、π/2（90°）反時計回りに回すということになります。これで速度の向きが円の接線向きだってでてきました。加速度はさらにπ/2（90°）反時計回りに回すということになります。さて、どちら向きでしょうか。（これそのまま練習問題そにょ２）

練習問題そにょ３　ある物体は変位1から点0を中心とし、半径1mで反時計回りに角速度πで等速円運動をしています。この物体の1秒後の変位を求めてください。

練習問題いっぱい出したからとても気持ちがいいので少し飲んで寝ます。おやすみなさーい

こたえ

練習問題そにょ１

練習問題そにょ２：１の答えにマイナスの符号がついているので、xと見比べると実数側、虚数側ともに反対、つまり点Pから見たら中心向き

練習問題そにょ３：-1