
Trader JOE v2 – Liquidity Bookの概要
概要
Trade JOE v2では、Liquidity Bookという仕組みを採用することで、スワップ価格への影響を軽減しながら、これまで以上に高い資本効率と柔軟性で流動性を提供することができます。また十分に流動性が提供されていれば、ゼロスリッページでのスワップ取引を行うことができるほか、volatility accumulatorと変動手数料の導入によって、Impermanent Lossの軽減に寄与します。Trader Joe v2のポイントとしてはゼロスリッページと指値注文の実現、柔軟な流動性の提供、変動手数料、それに伴うインパーマネントロスの軽減などが、着目すべき点と感じています。今回はホワイトペーパーを読み解きながら上記の点について解説を加えます。また私個人としては、最終部で記述しているボラティリティ・アキュムレーターとインデックスリファレンスの仕組みは、単純ですが、うまく設計されているなと感じました。
Liquidity Bookとは
Liquidity Book(以下、流動性ブック)は、資産ペアの流動性を離散的な価格ビン、わかりやすく言えば、特定の価格を割り当てた価格ビンによって構成されます。したがって仕組みとしては、DeFiで馴染み深いAMMというよりは、従来の株式市場などで導入されているオーダーブック方式に近いイメージです。流動性ブックにおいて、トークンの流動性はLPが指定した価格に応じてそれぞれの価格ビンに配置され、価格ビンに提供された流動性は、そのビンで指定された所与の価格によって交換されます。つまりTrader Joe v2の価格ビンは、板取引所の気配値とも言うべきでしょうか。
そして以下の図のように、すべての離散的な価格ビンを集約しているという点がオーダーブック方式に近いことの所以です。トークンX、Yの現在の市場価格は、トークンXとYの両方を含むビン(下図のP14)に割り当てられた価格と表現することができます。またその下の価格ビンはすべてトークンY(P11~P13)、上のビンはすべてトークンX(P15~P17)で構成されていることになります。現在の価格ビンの流動性が完全に変換されると(この図の場合P14の価格ビンにおいて赤もしくは青のトークンの1つだけで価格ビンが構成されることを意味します。)、価格は次のビンに移動します。各価格ビン内は固定価格であるため、スワップ時にスリッページが発生するのは、次の価格ビンの流動性も使用し、スワップを行った場合です。

具体的な流動性の提供仕組みは、下記で解説しますが、Uniswap v3などと同じように価格レンジごとに流動性を提供します。例えば、異なる市場参加者(色分けされている)が提供する市場の流動性構造は、下図のように表現することができます。
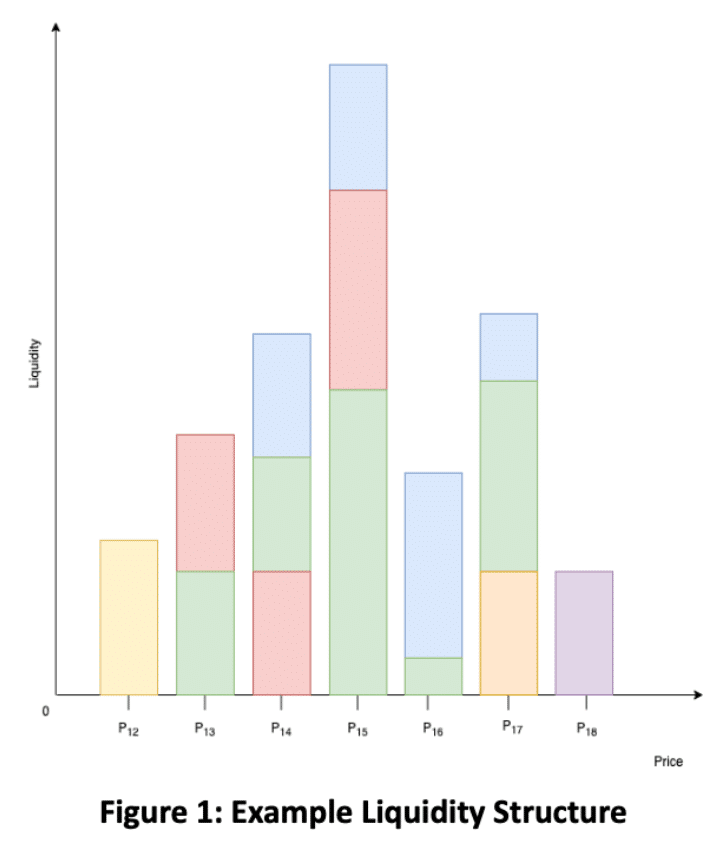
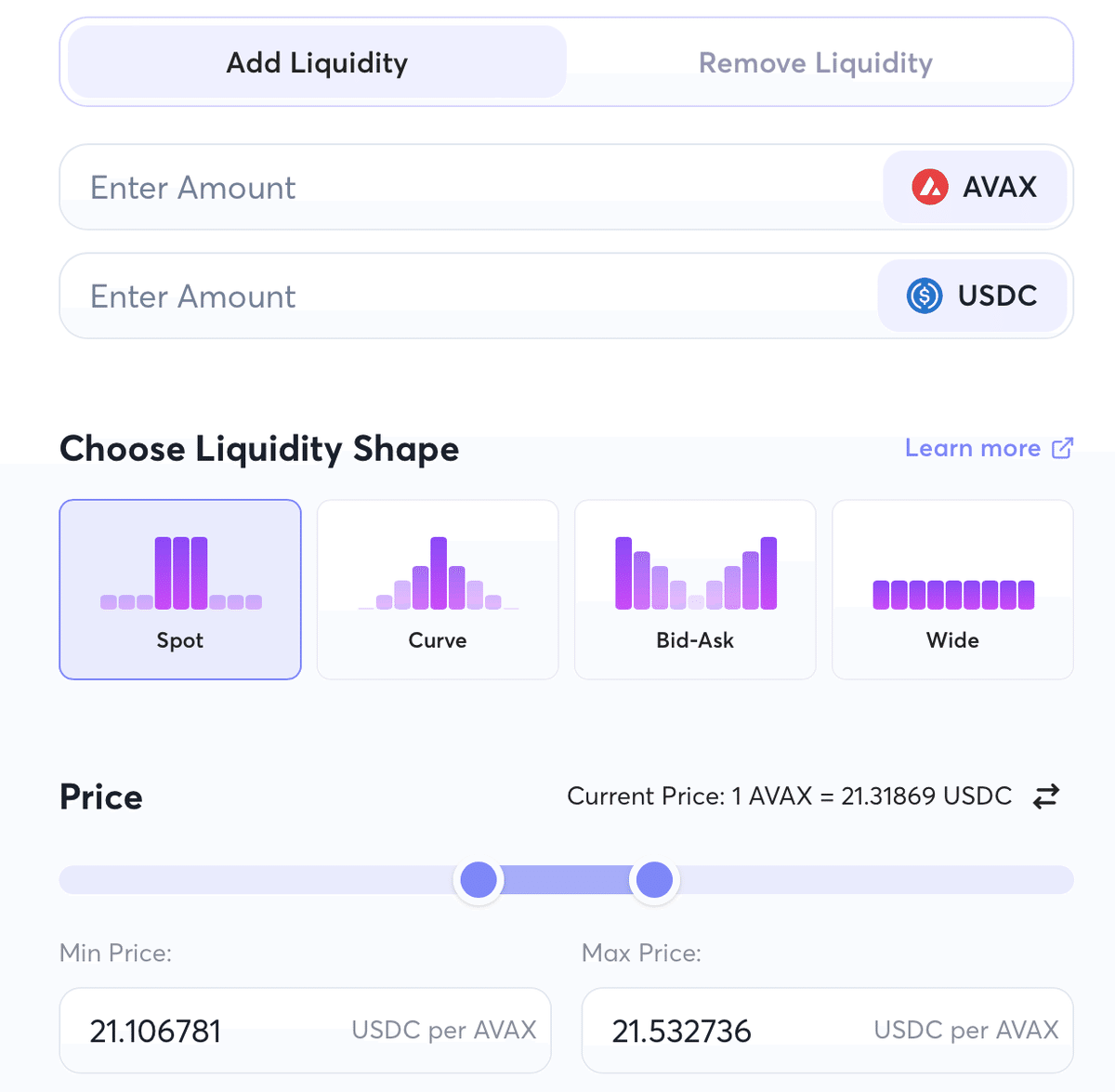
また以上のように柔軟な形で流動性を提供できます。Uniswapにおいては現状、WideかSpotの選択肢しかないわけですが、Trader Joeでは流動性提供の範囲だけではなくのCurveやBid-Askといった価格ビンごとにどれほど流動性を提供するかという点も選択できるようになります。価格ビン一つだけに流動性を提供すれば、事実上の指値注文も可能になります。筆者は、トレーダーではありませんが、正規分布もしくは、市況に応じて以下のように流動性の提供をすることが良いのではと考えています。ただいかなるも検証していません。

離散的である、連続的であるとは
離散的という言葉についても確認しておきましょう。例えば、離散変数とは取りうる値が飛び飛びになっている変数のことです。サイコロの出る目、トランプをランダムに一枚引いた時に出る数字の大きさ、数列などですね。反対語としては連続的という言葉があります。例えば連続変数とは、繋がった値をとる変数です。身長のように、170cmのこともあれば、170.11cmも取ります。さらに、170.000001cmというのも有り得え、無限に実数を取ることができます。他にも関数$${y = k/x}$$なども当てはまります。なぜなら$${x}$$にどんな実数(0以外)を代入しても$${y}$$が算出されるからです。一方数列は異なります。数列は$${n}$$が自然数です。したがって数列では連続的な数値の表現をすることができません。

様々な量的変数(離散変数/連続変数/パネルデータ/時系列データ/クロスセクションデータ)
これがUniswapとTrader Joe v2の違いの一つです。Uniswapでは連続な関数を採用しているため、原理上は、いかなる価格も提示することができます。(当然小数点の切り捨てが行われるので実際には全ての価格を表示することはできません。また正の実数の範囲内です。これ以降でも厳密な数学的な定義は行わず、あくまでイメージをつかむための表現とします。)一方、Trader Joe v2は離散的であるため、あらかじめ設定された所与の価格に応じて価格を提示します。この知識は後々の詳しくTrader Joe v2の仕組みを解説する際に必要となりますので、記憶に留めておいてください。ここであまりテクニカルで細かな部分に立ち入るつもりはありませんが、そもそもUniswapV3はtickという仕組みを採用しています。tickというのは価格に近い概念ではあるのですが、例えば、ETH-USDCのプールにおいて1000USDCから1500USDCに流動性を提供する場合、1000USDC-1500USDCの広いレンジで流動性を提供するというよりは、仮にtickspacingが100なら1000-1100,1100-1200,1300~というようにそのtickspaceごとに流動性を提供する仕組みとなります。そしてこの間のことをtickとtickの間をtickspacingと呼びます。このtickspacingは、基本的に手数料水準に基づいて決定され、UniswapV3の0.05%の手数料プールであれば、tickspacingは10が多く、0.3%のプールだと60というのが一般的です。例えUniswapV3がいくら指値的に機能しても、tickspacing内はUniwapV2ようになります。したがって必ずスリッページが発生するのです。
流動性ブックを可能にする仕組み
1. ビンの価格決定の仕組み
Trader Joe v2においても従来のAMM の仕組みを踏襲し、価格$${P}$$は、$${X}$$のリザーブの変化に対する$${Y}$$のリザーブの変化率として定義されます。したがって以下の式となります。
$${P = dy/dx}$$
ただTrader Joe v2では各ビンの価格は所与であるため、注意が必要です。具体的には従来型のUniswap等では、$${y = k/x}$$の式に基づき$${k}$$が所与とされ、交換に出される$${x}$$トークンの量と$${k}$$の値に基づいて価格が表示されます。一方先程から説明している通り、Trader Joe v2ではあらかじめ価格が所与となっています。具体的には価格ビン1の価格は0.9、価格ビン2の価格は0.95、価格ビン3の価格は1などとあらかじめ価格の決まったビンに流動性が供給され、スワップが行われます。
ここではビン毎の価格表示をどのように決定するかについてより詳しく解説を行います。まずTrader Joe v2の価格表示はその仕様上$${(2^{-128} ,2^{128} )}$$の範囲内で表現されます。
つまり$${1/340282366920938463463374607431768211456}$$以上340282366920938463463374607431768211456となるので要は0からほぼ無限大の価格帯まで表示対応できるということです。肝心の各ビンの価格$${P}$$を算出する式は以下となります。
$${P_i = (1+S)^{i-b} }$$
ひとまず各変数の概要を説明すると$${s}$$はビンステップと呼ばれる変数で0.0001から0.01の間で決定されます。$${i}$$はビン識別子と呼ばれる変数で$${b-N_b}$$から$${b+N_b}$$の間で定義されます。$${b}$$は価格ビンの中間点であり、ビン識別子$${i}$$の中間点です。また$${N_b}$$は以下の式により定義されます。各ビンに設定される価格は、下記の式に示すように,ペアのビン・ステップ$${s}$$およびビンの識別子$${i}$$の関数となります。
$${N_b = argmax_i (1 + s)^i < 2 ^{128} }$$
これだけ説明されてもよくわからない点も多々あるかと思うので、実際に数字を当てはめて説明したいと思います。まず価格$${P}$$に関してTrader Joe v2ではその仕様上$${(2^{-128},2^{128}) }$$の範囲内つまり0から無限大の価格帯まで表示対応することができます。次にビン識別子$${i}$$を定義します。しかしながら$${i}$$は$${b-N_b}$$から$${b+N_b}$$の間で定義されるので、$${b}$$と$${N_b}$$をあらかじめ決定します。$${N_b}$$を算出するにあたって、数学的な解説を加えたいと思います。式にある$${argmax}$$とは最大値となる$${i}$$の集合を返すという意味です。例えば$${y = - x^2 + 1}$$の関数において最大値maxは$${y = 1}$$ですが、その最大値$${y = 1}$$をとるような$${argmax}$$は$${x = 0}$$ということになります。
したがって今回の場合、$${s = 0.0001}$$とした場合、$${2^{128} }$$未満で$${1.0001^i}$$が最大となるような$${i}$$を計算しようとすると$${i = 887272}$$となります。また上記で述べた通り、$${N_b = argmax_i}$$なので$${N_b = i = 887272}$$とも表現できます。そしてこれはホワイトペーパー内に具体的な記述が存在しますが、価格ビンの数$${2^{24} }$$つまり8,388,608未満となります。そして$${b}$$は価格ビン数の中間点なので$${2^{23} }$$個目となり$${2^{23}}$$と表現されます。したがって$${s = 0.0001}$$の場合ビン識別子の範囲は、
$${i = [b-N_b b+N_b] = [8388608 - 887272, 8388608 + 887272]}$$
つまり$${i}$$は、$${(7501336 , 9275880)}$$
となります。したがってビン識別子が$${i = 7501336}$$の時、ビンの価格は、
$${P_{7501336} = (1+s)^{i - b} = (1+0.0001)^{7501336 - 8388608} = (1+s)^{- 887272} = 0.0000}$$
完全なゼロではないですが、ほとんどゼロといっていい数値が計算されます。
ビン識別子$${i = 8368608}$$の時、ビンの価格は
$${P_{8368608} = (1+s)^{i - b} = (1+0.0001)^{8368608 - 8388608} = (1+0.0001)^{- 20000} = 0.8187}$$
ビン識別子の時、ビンの価格は$${i = 8388608}$$
$${P_{8368608} = (1+s)^{i - b} = (1+0.0001)^{8388608 - 8388608} = (1+0.0001)^{0} = 1}$$
この時は双方のトークン価値は一緒ということを意味します。説明がかなり長くなりましたが、以上のようにあらかじめ各ビンあたりの価格が設定されます。ビンステップについて補足をすると、変動が激しいペアの場合、大きな値動きを許容するために、比較的高いビン・ステップを採用します。一方小さなビンステップは、USDC.e-USDCのように、より狭い範囲で取引されることが予想されるペアでより有用です。つまりビンステップが大きくなると、価格ビン同士のスリッページが大きくなります。
ビン内の流動性計算の仕組み
流動性(L)は、ビンに預けられたリザーブの名目価値と定義されます。個々のビンの流動性は資産ペアのリザーブ量に応じて決定され、所与の価格に基づき独自のボンディングカーブを構築します。具体的には、$${y}$$を切片、$${P}$$を傾きとする以下の一次関数の式により個々のビンの流動性が定義されます。
$${P_i * x + y = L}$$
補足:
変数$${y}$$に価格がかけられていないのは正確には1がかけられているからです。例えば3:5の比率でスワップが行われるとは、価格比の意味通り、$${1 : 5/3}$$で交換が行われているとも捉えられます。またこの式からTrader joe v2においては、十分な流動性が保たれている場合、ゼロスリッページでのスワップ取引が可能となることを示唆します。よくAMMにおけるトークン価格はLPトークン量の比で表現されますが、私自身は、微分であると認識すべきだと思います。というのも$${y = k/x}$$をxについて微分すると、$${y = k/- x^2}$$となり、xトークンの量が少しでも変化すれば価格は変化します。しかしながら$${P_i * x + y = L}$$を微分すると$${P_i + y = 0}$$であるのでxトークンの量が変化しようとも価格は変化しません。

ビン内のリザーブ構成比
流動性ビンにおける各資産の利用可能なリザーブ割合を示すために、構成係数$${C}$$を導入します。そしてそれは以下の式で示されます。
$${C = y/L}$$
資産$${y}$$の流動性構成比
$${y = CL}$$
資産$${x}$$の流動性構成比
$${x = L/P_i * (1 - C)}$$
これを図示すると以下のようになります。

流動性提供
ここでは流動性提供を行う際に、どのように流動性の計算がなされるのかについて概観します。流動性の計算において考慮しなければならないのは自分がどの範囲に流動性を提供するのかということです。特に現在価格のビン(アクティブなビン)を含む場合とそれ以外の価格のビン(非アクティブなビン)の範囲で流動性を提供する場合とを区別する必要があります。これまでの説明にもあった通り、現在価格未満のビンにはトークンXのみが存在し、現在価格より大きいビンにはYトークンのみが存在します。しかし現在価格のビンにはトークンX、Yの双方が存在するため、流動性の計算式がわずかに異なります。実際に確認しますが、式変形を行うだけなので決して難しくはありません。まず現在価格のビン以外でのビンの資産$${y}$$の流動性を計算します。
現在価格ビン以外のビンの資産$${y}$$の流動性計算式
$${ L_{c=1} = \Delta y}$$
資産$${y}$$の流動性構成比が以下のように表せることを利用します。$${C}$$はトークン同士の流動性比率
$${y = CL}$$
資産$${y}$$の非アクティブなビンには、トークン$${y}$$しか存在しません。したがって$${C = 1}$$となります。すると$${y = L}$$と表すことができ、あとは変化量を表すデルタを加えれば
$${\Delta L_{c=1} = \Delta y}$$
となります。価格は1なのでこれは10枚のトークンが
現在価格ビン以外のビンの資産$${x}$$の流動性計算式
資産$${x}$$の流動性構成比が以下のように表せることを利用します。
$${x = L/P_i * (1 - C)}$$
資産$${x}$$の非アクティブなビンには、トークン$${x}$$しか存在しません。したがって$${C = 0)}$$となります。すると$${x = L/P_i }$$と表すことができ、これを$${L = /P_i *x}$$と式変形し、変化量を表すデルタを加えれば
$${\Delta L_{c=0} = /P_i * \Delta x}$$
となります。次に現在価格のビンの流動性を計算します。現在価格のビンであっても資産ごとに流動性を計算しますが、その手順がわずかに異なります。
現在価格ビンの資産$${y}$$の流動性計算式
$${\Delta L = 1/C * \Delta y}$$
資産$${y}$$の流動性構成比が以下のように表せることを利用します。
$${y = CL}$$
現在価格のビンには、トークン$${y}$$とトークン$${x}$$の両方が存在します。したがって$${C}$$はそのままに、$${y/C = L}$$と式変形し、変化量を表すデルタを加えれば
$${\Delta L = 1 / C)* \Delta y}$$
現在価格ビンの資産$${x}$$の流動性計算式
$${\Delta L = P /(1 - C)* \Delta x}$$
資産$${y}$$の流動性構成比が以下のように表せることを利用します。
$${x = L/P_i * (1 - C)}$$
現在価格のビンには、トークン$${x}$$とトークン$${y}$$の両方が存在します。したがって$${C}$$はそのままに、$${L = P/ (1 - C) * x}$$と式変形し、変化量を表すデルタを加えれば
$${\Delta L = P /(1 - C)* \Delta x}$$
スワップ
スワップに関しては以下の式にて実行されます。特質すべき点としてTrader Joe v2では、一つの価格ビンに十分な流動性が存在する場合、ゼロスリッページでトークンのスワップを実行できることです。Uniswap等では$${y = K/x}$$の定積式を採用しており、どれだけ十分に流動性供給が行われていても、わずかにスリッページが発生します。一方Trader Joe v2では各価格ビンは$${P_i * x + y = L}$$の一次関数で表現されるため、上段で申し上げた通り、現在の価格ビン内の流動性で対応できれば価格$${P_i}$$によってスワップが行われます。もちろんスワップが現在の価格ビンで利用可能な量以上の流動性を必要とする場合、隣接する価格ビンに移動し、スリッページは発生します。以下スワップ時の計算式になります。
$${\Delta y = - P \Delta x}$$
ここではUSDC-USDT(両トークンともきっかり1ドルを想定、トークン$${x}$$をUSDC、トークン$${y}$$をUSDT)のペアを例に説明します。
$${P = 1}$$なので$${\Delta y = - \Delta x}$$となり、例えば10USDTを10USDCにスワップする場合、$${\Delta y = \Delta 10 = - \Delta x = - \Delta 10}$$となり交換が行われました。
スワップ手数料の仕組み
Trader Joe v2においては変動手数料制が導入されています。これは従来、Uniswap v3などの集中流動性を採用しているDEXにおいて流動性を提供することは、高い資金効率によるリターンが期待できる一方、そのリスクも高まります。調査(https://cointelegraph.com/news/half-of-uniswap-v3-liquidity-providers-are-losing-money-new-research)によると、Uniswap v3の流動制提供者の約50%は、インパーネントロスの影響により、マイナスのリターンを計上しています。インパーネントロスは、LPポジションに含まれる2つのトークンの価格比が変化し、リバランスされた結果発生する相対的損失です。したがってステーブルコイン同士やAVAX-sAVAXというペアでの流動制提供では、重要ではありませんが、例えばUSDC-AVAXペアでは価格比が大きく変化します。この価格比の変化に着目し、価格の変動が大きい場合、つまり市場のボラティリティが高い場合には、スワップ手数料も上昇し、低い場合には手数料が低下する仕組みをTrader Joe v2では採用しています。
この仕組みにより、流動性提供者はインパーマネントロスを軽減することができ、またポジションの変更をより手軽にします。ここからは具体的はTrader Joe v2の手数料体系について概観します。まずスワップ手数料$${f_s}$$は、基本手数料$${f_b}$$と今回新たに採用される変動手数料$${f_v}$$で構成されます。スワップ手数料のレートは各価格ビンのスワップ額に応じてそのビン内の流動性提供者に比例配分されます。スワップ手数料は流動性とは別で流動性提供者が請求することになります。$${n}$$個のビンを跨いでスワップが行われた際の手数料の合計は、以下の式に従って計算します。
$${f_s = \sum_{i=1}^n [(swap amount)_k * (f_b +f_v)_k]}$$
式の意味としては基本手数料と変動手数料をスワップされる金額でかけ、スワップが起きた回数足し合わせるという意味です。具体的には基本手数料$${f_b = 0.3% = 0.003}$$と仮に変動手数料$${f_v = 0.1% = 0.001}$$の場合、両者を足し合わせ合計の手数料は$${f_b +f_v = 0.003 + 0.001 = 0.004}$$となります。上記の条件で1000ドルのスワップが10回執行されたとすると$${(swap amount) * (f_b +f_v) = 1000 * 0.004 = 4}$$であり、10回の場合$${f_s = 4 * 10 = 40}$$で40ドルがスワップ手数料となります。
基本手数料
基本手数料のレートは以下の式で決定されます。
$${f_b = B * s}$$
上記の式で示されているように、ビンステップ(s)と基本料金係数(B)の積で決定されます。例えば$${s = 0.0001, B = 0.1 }$$の場合、基本手数料は$${f_b = B * s = 0.0001 * 0.1 = 0.00001}$$となります。また基本手数料は,その名の通りすべてのスワップの最低レートを表しており、スワップ手数料のレートがこの値以下になることはありません。
変動手数料
変動手数料のレートは以下の式で決定されます。
$${f_v(k) = A(v_k * s)^2}$$
変動手数料の決定の仕組みは上記の式に加え、新たに導入されたボラティリティを計測するボラティリティ・アキュムレータ変数$${v_a(k)}$$の理解が不可欠となります。Aは変動手数料管理パラメーターというもので、こちらも気になりますが、解説が見つかりませんでした。
ボラティリティ・アキュムレータとは
ボラティリティは、時間の経過とともにどれくらい価格ビンが跨がれたのかと言う点から計測します。具体的にはスワップが行われる際に、その取引がいくつのビンをまたぐのか、そして最後のスワップからどのくらい時間が経過したのかを追跡することによって、市場のボラティリティを測定する方法です。プライスインパクトのあるスワップが短期間に連続して行われた場合、この数値が上昇します。取引の動きが鈍くなる場合には、数値が減衰し始め、特定の時間枠の間にスワップが発生しない場合はリセットされます。具体的には下記の式によって定義されます。
$${v_a(k) = v_r + \vert i_r - (activeId+k)\vert}$$
$${v_r}$$とはボラティリティリファレンスと呼ばれ、直前の取引からの時間の経過に伴い変化する変数です。$${t}$$は直前のトランザクションとの時間の差分として定義されます。 この$${v_r}$$の決まり方以下の式に依拠します。
$${v_r = \begin{cases} v_r t < t_f \\ R*v_a t_f\leqq t < t_d \\ 0 t_d \leqq t \end{cases}}$$
結論として$${t}$$が小さければ小さいほど、つまり直前のトランザクションとの時間の差分小さいわけで、盛んに取引が行われていることを示すわけです。このボラティリティリファレンスではフィルターピリオドと呼ばれる$${t_f}$$とディケイピリオドと呼ばれる$${t_d}$$がその閾値として設定されています。つまり$${t_f}$$とフィルターピリオドを下回るほど短いスパンで取引が行われる、いいかれば盛んに取引が行われれば、ボラティリティリファレンスでは$${v_r}$$が適応されます。逆にディケイピリオド上回るほど取引と取引の間に時間差が生ずれば、このボラティリティリファレンスは0で適用されません。
例を示せば以下になります。
$${v_r = \begin{cases} v_r t < 5sec \\ R*v_a 5sec\leqq t < 10sec \\ 0 10sec \leqq t \end{cases}}$$
直前の取引との時間差が3秒であれば、$${v_r}$$が適応されるし、20秒くらいあいてしまったら、0になりボラティリティリファレンスは適応されません。次にインデックスリファレンス、$${i_r}$$ついて解説します。このホワイトペーパーで私が最も関心した点がここです。基本的に$${i_r}$$は、以下のように現在の価格ビンを参照します。しかしながら、フィルターピリオドを下回るほど取引頻度が高い場合、過去の価格ビンを参照します。
$${i_r = \begin{cases} i_r t < t_f \\ activeID t_f\leqq t \end{cases}}$$
おそらくこれだけではこの$${i_r}$$の凄さを感じにくいかと思いますので、このボラティリティ・アキュムレータと変動手数料の解説を含め、例を元に概観しましょう。同じような例がTrader Joe v2のDocsにもありますので、そちらも是非ご覧下さい。
$${t_f = 5sec, t_d = 10secs, R = 0.5}$$とし、現在価格ビンを1000とします。
状況1
Aさんは、2つの価格ビンを跨ぐスワップ取引を以下の条件で執行したとします。
現在価格 $${i_r = 1000}$$
直前のトランザクションはひとまず考えないものとし、
$${v_r = 0}$$とする。
$${v_a(0) = 0+\vert 1000 −(1000+0)\vert = 0}$$
$${v_a(1) = 0+\vert 1000 −(1000+1)\vert = 1}$$
$${v_a(2) = 0+\vert 1000 −(1000+2)\vert = 2}$$
したがって現在価格は1002に変動し、各価格ビンでの$${v_a(k)}$$が定義されました。
状況2
Bさんは、Aさんの取引から9secs後に4つの価格ビンを跨ぐスワップ取引を以下の条件で執行したとします。
現在価格 $${i_r = 1002}$$
$${v_r = 0.5*2 =1}$$とする。
$${v_a(0) = 1+\vert 1002 −(1002+0)\vert = 1}$$
$${v_a(1) = 1+\vert 1002 −(1002+1)\vert = 2}$$
$${v_a(2) = 1+\vert 1002 −(1002+2)\vert = 3}$$
$${v_a(3) = 1+\vert 1002 −(1002+3)\vert = 4}$$
$${v_a(4) = 1+\vert 1002 −(1002+4)\vert = 5}$$
したがって現在価格は1006に変動する。
ここからがポイントでインデックスリファレンスの設計の妙をご覧いただきたい。最初に結論から申し上げると、インデックスリファレンスを用いることで、ボラティリティ・アキュムレータが、いってこい(同じ日のうちに相場が同じ幅だけ上がって下がり(またはその反対)、結局、前日の引け値と同水準に落ち着くこと。大和証券 金融・証券用語解説より、https://www.daiwa.jp/glossary/YST0072)的な要素も適切に反映できるということです。つまりこの仕組みはLPのインパーマネントロスを和らげる働きがあるわけですが、LPにとって一番嬉しいのは価格変動が起きないことではなく、自らが提供している流動性の範囲で呆れるほど価格変動が発生して、LP解体時に価格が戻って手数料を稼ぎまくれることです。
一方インデックスリファレンスによって断続的に価格が下がり続ける場合にのみ、ボラティリティ・アキュムレータが、その効果を発揮します。以下では状況3と題して、改めてインデックスリファレンスが存在する場合と存在しない場合に分けて上記の内容を確認します。
状況3
インデックスリファレンスが存在しない場合
価格上昇時
Cさんは、Bさんの取引から1secs後に2つの価格ビンを跨ぐスワップ取引を以下の条件で執行したとします。
現在価格 $${i_r = 1006}$$
$${v_r = 5}$$とする。
$${v_a(0) = 5+\vert 1006 −(1006+0)\vert = 5}$$
$${v_a(1) = 5+\vert 1006 −(1006+1)\vert = 6}$$
$${v_a(2) = 5+\vert 1006 −(1006+2)\vert = 7}$$
したがって現在価格は1008に変動する。
価格下落時
Cさんは、Bさんの取引から1secs後に2つの価格ビンを跨ぐスワップ取引を以下の条件で執行したとします。
現在価格 $${i_r = 1006}$$
$${v_r = 4}$$とする。
$${v_a(0) = 5+\vert 1006 −(1006+0)\vert = 5}$$
$${v_a(1) = 6+\vert 1006 −(1006-1)\vert = 6}$$
$${v_a(2) = 7+\vert 1006 −(1006-2)\vert = 7}$$
したがって現在価格は1004に変動する。インパーマネントロス自体は軽減されるのに、つまりLPへの還元は必要ないのにもかかわず、$${v_a(k)}$$は、上昇してしまっている。非対称的に価格変動を評価する仕組みが必要なのである。
状況3
インデックスリファレンスが存在する場合
価格上昇時
Cさんは、Bさんの取引から1secs後に2つの価格ビンを跨ぐスワップ取引を以下の条件で執行したとします。
$${i_r}$$と$${v_r = 4}$$は、過去の価格を参照するため、状況1の1002を採用するほか、
$${i_r = 1002}$$
$${v_r = 1}$$とする。
$${v_a(0) = 1+\vert 1002 −(1006+0)\vert = 5}$$
$${v_a(1) = 1+\vert 1002 −(1006+1)\vert = 6}$$
$${v_a(2) = 1+\vert 1002 −(1006+2)\vert = 7}$$
したがって現在価格は1008に変動する。断続的に価格が上昇しているわけなので、インパーマネントロスが悪化しており、変動手数料によるカバーが必要。
価格下落時
Cさんは、Bさんの取引から1secs後に2つの価格ビンを跨ぐスワップ取引を以下の条件で執行したとします。
$${i_r}$$と$${v_r = 4}$$は、過去の価格を参照するため、状況1の1002を採用するほか、
$${i_r = 1002}$$
$${v_r = 1}$$とする。
$${v_a(0) = 1+\vert 1002 −(1006+0)\vert = 5}$$
$${v_a(1) = 1+\vert 1002 −(1006-1)\vert = 4}$$
$${v_a(2) = 1+\vert 1002 −(1006-2)\vert = 3}$$
したがって現在価格は1004に変動する。インパーマネントロス自体は軽減されるのに、つまりLPへの還元は必要ない。したがって$${v_a(k)}$$は減少している。
個人的に、集中流動性の実装はLP同士の格差を広げるため、どちらの方向に価格が向かっても変動手数料の恩恵に預からせて上げてよと感じる。しかしながらこれを認めてしまうと、不正に売買を進め、変動手数料の仕組みが操作されてしまう恐れがあるので、致し方ない。
以上がホワイトペーパーからみるTrader Joe v2の概要です。訂正、議論等あればコメント欄の方にいただけると幸いです。
