
ステーブルコインの新たな仕組みcrvUSDとは
本記事の概要
今回は昨年11月22日に公開され、仕組みが非常に難解なことでも有名なcrvUSD、特にLLAMMAついて解説をします。本記事の理解に当たってはUniswap v3とMakerDAOが発行するDAI(レンディングプラットフォームのAaveやcompoundでも十分)に関する知見が有用ですが、その知識がゼロであっても順次、簡単な説明を加えているので全く問題ありません。本記事は、curve stablecoin designというcurve finanaceのホワイトペーパ(https://github.com/curvefi/curve-stablecoin/blob/master/doc/curve-stablecoin.pdf)を元にしており、その他出典は順次掲載しています。何分間違いもあるかと思いますが、コメント欄等でお知らせいただければ幸いです。
前提
crvUSDの理解を進めるにあたって現状のステーブルコイン、特にMakerDAOのDAIに代表されるようなCDPを用いたステーブルコインの問題点について考える必要がある。ここでは主に3点あげる。まず第一にユーザーはステーブルコインを発行するために担保をプロトコルに預け入れるが、その担保が一気に清算されてしまうリスクである。具体的な例を挙げるとユーザーAさんはMakerDAOを利用して、ETH価格が1000ドルの時点で、10ETHの担保を預け入れ、5000DAI(5000ドル)を発行した。よって担保率は200%である。しかしながらある事件をきっかけにETH価格が一気に50%下落し、1ETH = 500ドルとなってしまった。担保率は100%であり、MakerDAOが求めるETH担保比率の150%を下回ってしまった。よって清算が発生する。これはMakerDAOに限った話ではないが、そのユーザーの担保は半額、最悪の場合一度に全額が清算されてしまうのである。したがってユーザーは、常に担保資産の価格について気を配らねばならない。もちろん担保比率を例えば300%、400%と高めることで大きな価格変動に備えることができるが、これは資金効率が非常に悪くなってしまうというトレードオフの関係にある。第二に、ユーザーは清算されてしまった担保を取り戻すことが出来ないという点である。基本的に多くのCDP型ステーブルコインのプロジェクトやレンディングプロジェクト(同じような仕組みを採用)では、オークションを通じて清算人がユーザーの担保を清算してしまうため、ユーザーには担保が返却されない場合も多々ある。第三に多額の資金を運用するような機関投資家や個人、いわゆるクジラが清算された場合には、その担保資産の市場価格が一気に下落し、連鎖清算に陥るような状況も想定される。これは暗号資産市場全体にとって好ましくない。以上の大きく3点の問題点が挙げられる。以上の問題に新しい解決策を提示したのがcrvUSDであり、今回はその仕組みにおいて最も重要な機能となるであろうLLAMMAを中心に詳しい解説を行いたい。
crvUSDとは
crvUSD自体は上記の通りCDP型のステーブルコインで、例えば1ETH = 1000ドル時点において10ETHを担保に5000crvUSD(5000ドル)を発行するという格好である。ここまで一般的にプロジェクトと相違ないがcrvUSDがの特色は、LLAMMAを用いた清算プロセスにある。CDP型のステーブルコインであるから規定された担保率を下回れば清算が開始される。しかしながらcrvUSDでは、瞬間的な清算の代わりにバンドという仕組みを用いることで段階的に清算が執行される。
バンドとは

具体的には、上記の図(赤色の線でマークした部分)のようにcrvUSDの担保価格はいくつかのバンドに分割されている。特定の清算価格ではなく、清算価格の範囲によって担保を預け入れる。上記の例では10ETHの担保資産を清算価格990ドルを皮切りに10ドルのレンジで清算が執行するように設定してある。図からはAMM priceつまり現在の市場価格が987ドルであるため、清算が進行しており496ドル分のETHがcrvUSDに変換されている。したがってcrvUSDの量を示すxが496.13、ETHの量を示すyが1.475と減少しているのが確認でき、このことは青丸で囲ったグラフからも読み取れる。(補足 : xがcrvUSDの量、yが担保資産であるETHの量)このことバンドで示すと以下となる。断続的にETHの価格が下落すれば、担保は全てcrvUSDになってしまい、価格が回復すれば担保はETHに戻る。
バンド 99 ($980 - 現在価格 ($987) - $990): 496crvUSD、1.475ETH
バンド 98 ($970 - $980): 2ETH
バンド 97 ($960 - $970): 2ETH
バンド 96 ($950 - $960): 2ETH
バンド 95 ($940 - $950): 2ETH
バンドの解説が一段落したところで、本題のLLAMMAの解説に移ろう。ここで多くの人が考えるのは、なるほどcurve v2の流動性を使ってバンドごとに順次スワップ取引が執行され、清算が起きていると。しかしながらよくよくAMMの仕組みを考えればそんなこと容易ではないし、現に違う。では何が起きているかをUniswap v3を用いて考えると、要は現在価格以下の部分にLPとして流動性供給を行なっているのである。(多くの人が違和感を感じると思うが一旦読み進めていただきたい。)わかりやすく現在価格以下の範囲でUniswap v3を用いて流動性供給している例を以下で示す。
crvUSD理解のための準備をUniswap v3を例に

資産の価格が下落すれば、つまり担保率を割るような価格に到達すればUniswap v3と同様にLP の資産が徐々に変換されていく。この仕組みを用いて担保を徐々に清算していく。(価格が回復すれば担保資産に再変換されるのは、LPに流動性を提供されている方なら自明な話であろう)下記の図ではそのことを示しているが、価格の下落を再現できないため、現在価格をまたぐように流動性供給をすることで同様のことを示す。実際に資産のETHとUSDC 同士で資産の比率が変化しているのがわかる。

ここでこの記事を読まれている方全員がこの説明ではcrvUSDは成り立たないだろ!!!と考えていると思う。なぜならUniswap v3の場合(Uniswap v3に限らず集中流動性を実装するAMM全て)、現在価格が流動性提供の範囲を上回っている場合、LPの資産は全てUSDCになる。そして現在価格が流動性提供の範囲内にあれば、LPプールはETHとUSDCによって構成される。ETH価格が下落していけば当然LPのプール内においてETHの枚数が増える(ETHが売られているので)。最終的に現在価格が流動性提供の範囲を下回るとプールはすべてETHで構成されることとなる。一方crvUSDに求められているのは、従来のAMMの仕組みと全く逆のことである。つまり担保資産であるETHの価格が下落しているにも関わらず担保LPのプールでは、ETHの枚数が減少し、crvUSDの枚数が増加するという仕組みを構築しなければならない。CurveはLLAMMAの仕組みを通じて上記の仕様の実装に理論上成功し、この事実こそがcrvUSD、LLAMMAおいて最も特筆すべき点である。ここからはcrvUSDのホワイトペーパーを確認しながら具体的仕組みについて理解を深めていきたい。
LLAMMAの詳細概要

この図に関しては、筆者自身も完璧に理解できているか不安なところではあるが簡単な解説を行う。この図はUniswap v3などいわゆる集中流動性をもつAMMの仕組みをcrvUSDの仕組みに当てはめながら表現した図である。いくつかの言葉をあらかじめ説明すると、縦軸の$${P_{AMM}}$$というのは、当然AMM上の価格であり、横軸の$${P_{center}}$$というのは流動性提供範囲の真ん中の価格である。$${P_{cu}}$$は流動性提供範囲の上限であり、$${P_{cd}}$$は下限である。$${p}$$は、AMMが算出する独自の価格でなく、いわゆる市場価格である。$${P_{center}}$$を上昇させれば、$${P_{AMM}}$$上でも価格は高く表記されるので線形の関係にあり、右上がりの線が引かれる。この図自体はUniswap v3シミュレーターでその状況を説明すれば、赤丸の部分を中心に表現されたグラフである。赤丸の部分はつまり以下のような状況である。

これに加えてUniswap v3では、現在価格が流動性提供の上限$${Pcu}$$を上回っている場合、LPの資産は全てUSDCになり、下限$${Pcd}$$を下回っている場合、LPの資産は全てETHとなることが表現されている。続いてはホワイトペーパーで挙げられているその下の図を説明したい。これが本題のcrvUSDの仕組みを説明する図である。
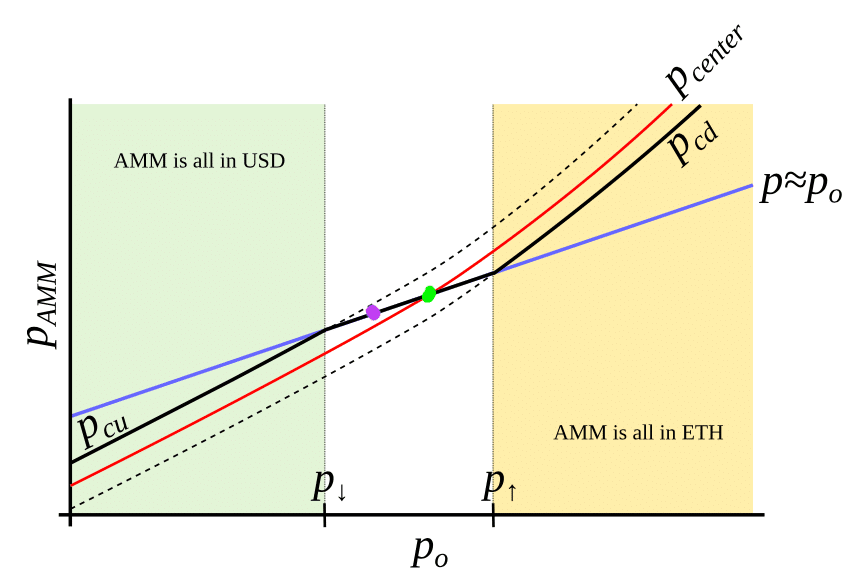
x軸が$${P_o}$$に変更されている点に注意したいのと$${P\uparrow}$$は清算開始価格、$${P\downarrow}$$は清算完了価格である。今度は青い線が線形の関係になっているが、x軸が$${P_o}$$に変更されているから当たり前で、$${P_o}$$が上昇すれば$${P_{AMM}}$$も上昇する。しかしながらこの図において最も特筆すべきはcrvUSDのLPプールにおいて仮に$${P_{center}}$$をLPプールの基準価格(緑色の点)とすると$${P_{center}}$$が$${P_o}$$の関数となっており(この点は以下で詳しい解説を加える)、現在価格を中心に、基準$${P_o}$$より$${P_{center}}$$の傾き、変化率が高くなっているのである。上記の点がどのように優れているかを改めて図を用いて説明すると、例えばETHの市場価格$${P_o}$$が下落し、緑の点から紫の点に移動したとする。すると従来のAMMにおいては$${P_{AMM}>P_o}$$という関係が瞬間的には成立する。しかしながらアービトラージャーが存在するため、USDがLPプールから抜けていき、結局$${P_{AMM} = P_o}$$となる。したがってLPプール内のETH枚数は増えている。一方crvUSDの清算LPプールにおいては、$${P_{center}}$$が$${Po}$$の関数であり、非線形なグラフの形をとるため、$${P_{center} < P_o}$$という関係が瞬間的に成立している。したがってcrvUSDの清算LPプール内ではアービトラージャーによってETHが買われ、つまりETHが清算LPプールから抜けていき、$${P_{center} = P_o}$$となる。$${P_{center} < P_o < P_{AMM}}$$が一時的に成立しているのである。意図的に清算LPプールの価格形成の仕組みを変えることで、上記の設計を可能にしている点がcrvUSDの最も重要な発明である。実際にホワイトペーパーに記載されている数式をもとに、上記の状況を再現すると以下となる。赤色の線を清算LPプール内のETH価格とし、市場価格をオレンジの線がクロスした青色の線上の点とする。清算LPプール内のETH価格と市場価格との差が縮まる様子が示されており、ETH価格は下落するがUSDの量は増加している。

crvUSDの数式解説をざっくりと
ここからはcrvUSDのホワイトペーパーに記述されている数式の意味についてその理解を深めていきたい。ただ基本的に線形的な市場価格と比較して、どのようにcrvUSDの清算プールが変化率の大きい価格を提供できるかについてを数式面から概観する。crvUSDのホワイトペーパーの中ほどにある数式の話で、全く受け付けない方もいるだろうが、重要なのは先程の仕組みなので読み飛ばしもらっても構わない。ただ、なるべくわかりやすく解説するつもりである。Uniswap3と同じように、今回はcrvUSDの量をx、ETHの量をyとする。するとトークン同士の増減も加味した定積式は以下のようになる。
$${I =(x+f)(y+g)}$$
$${f}$$と$${g}$$がトークン量の増減を表しており、また、$${x′≡x+f}$$と$${y′≡y+g}$$のように表現すれば、おなじみ$${I = x′y′}$$と書ける。(表現は少し異なるが、$${xy = k}$$という式は多くの方がAMMの説明をご覧になる際に目にした式だと思う。)この$${f}$$と$${g}$$が外部の価格オラクルによって変化する関数なのである。では続いて
$${P\downarrow/P\uparrow = A - 1/A}$$
これは、序盤で解説した清算バンドの幅を決定する式である。ちなみにバンド数自体は最小で5つのバンド、最大で50のバンドが選択可能である。範囲が大きければポジションの清算が早く始まり、より緩やかに清算が執行される。一方範囲が狭ければ、ポジションの清算は遅く始まるが、急激に清算が進む。私個人としては、上記の式よりも以下のように式変形した方が見通しは良いかなと思うので、これを採用します。
$${P\downarrow = A - 1/A*P\uparrow}$$
清算開始価格を1000ドルに設定し、$${A = 100}$$とする。この場合
$${P\downarrow = 100 - 1/100*1000 = 990}$$なのである清算レンジは1000ドルから990ドルとなる。ホワイトペーペーの11番の式に飛ぶが、清算レンジは5つから最大50までが想定されているため、上記の式を複数バンドに拡張したのが11番の以下の式である。
$${P\uparrow(n) = (A - 1/A)^n*P_{base}, P\downarrow(n) =(A − 1/A)^{(n + 1)}*P_{base}}$$
今回は簡略化のために2つのレンジで例を上げる。$${P_{base} = 1000}$$とし、引き続き$${A = 100}$$とする。この両者自体はどう決まるのかという声が上がりそうだが、ホワイトペーパーに記述がなかったので、省略する。
$${P\uparrow(1) = (100 - 1/100)^1*1000 = 990, P\downarrow() = (100 - 1/100)^(1+1)*P_{base} = 0.9801*1000 = 980.1}$$
$${P\uparrow(2) = (100 - 1/100)^2*1000 = 980.1, P\downarrow() = (100 - 1/100)^(2+1)*P_{base} = 0.970299*1000 = 970.299}$$
したがって清算バンドは以下の表記になる。
バンド 1($980 - $990)
バンド 2($970 - $980)
次にホワイトペーパーの(3)の式だが、これが市場価格を用いて清算プールの価格上昇率を非線形にする関数である。
$${f = P_o^2/P\uparrow * A *y_0 , g = P\uparrow/P_o * (A - 1) * y_0}$$
(4)の式は、清算プール価格$${P}$$の時に、市場価格$${Po}$$と$${P\uparrow}$$が同一である場合の式を示している。つまり清算開始価格に到達し清算が開始する状態を示した図である。また$${y = y_0}$$と$${x = 0}$$も条件として加わっている。
$${I = x + f/y + g = x + P_o^2/P\uparrow * A *y_0/ y + P\uparrow/P_o * (A - 1) * y_0 = 0 + P_o^2/P_o * A *y_0/ y_0 + P_o/P_o * (A - 1) * y_0 = P_o * A * y_0/ y_0 + (A - 1) * y_0 = P_o * A^2 * y_0^2}$$
(5)の式は清算プール価格を示す式であり、価格というのはつまるところ、定積式の微分なので以下の式となっている。トークンの量の比率と言っても問題ない。
$${p = dx'/dy' = x'/y' = f + x/g + y}$$
ここまでで各関数、変数の意味と関係が理解できたかと思うが、まだ明らかになっていない変数が一つある。それは$${y0}$$である。$${P\downarrow}$$と$${P\uparrow}$$は先程の式でAに関しては定数であるとの記述があり問題ない。また$${P_o}$$は市場価格、$${x}$$と$${y}$$はバンド内の流動性であるからこれも明らか。ホワイトペーパーの(6)、(7)の式によって清算開始時の$${y_0}$$を算出することで$${f,g}$$が市場価格$${P_o}$$の関数となるようにしたいのである。
$${(P_o^2/P\uparrow*A*y_0+x)(P\uparrow/P_o*(A−1)*y_0+y) = P_o * A^2 * y_0^2}$$
式を展開して
$${P_o * A^2 * y_0^2 - (P\uparrow/P_o *(A - 1)* x + P_o^2/P\uparrow*A*y_0) - xy = 0}$$
上記の方程式を解き、$${y_0}$$を算出する。
以上がcrvUSDのLLAMMAの解説になる。
