内積とはなんや

参考

内積は意味や使い方を複数持つため、１つの側面のみに着目しすぎると他の側面で使用された場合にわけわからんなりますことに注意します。

内積とはベクトルとベクトルを受けてスカラーを吐く演算です。
スカラーとは単一のパラメータであるようなもの、簡単に考えるならただの１つの実数です。ベクトルは複数のパラメータ（簡単に考えるならただのスカラー、難しく考えるなら複素数やら関数やらなんでも）を組み合わせたものであり、２つ組み合わせれば２次元ベクトル。３つ組み合わせれば３次元ベクトルです。プログラム的には配列に相当します。

演算規則

内積の定義

幾何学的定義：

二つのベクトル $${\mathbf{A}}$$ と $${\mathbf{B}}$$ の内積は、次の式で表されます。

$$
\mathbf{A} \cdot \mathbf{B} = |\mathbf{A}|  |\mathbf{B}| \cos \theta
$$

$${|\mathbf{A}|}$$、$${|\mathbf{B}|}$$ はそれぞれのベクトルの大きさ（ノルム）。
$${\theta}$$ は二つのベクトル間のなす角。

成分表示：

ベクトルを成分で表すと、内積は各成分の積の総和になります。

二次元ベクトルの場合：

$$
\mathbf{A} = (A_x, A_y)\\
\mathbf{B} = (B_x, B_y)
$$

$$
\mathbf{A} \cdot \mathbf{B} = A_x B_x + A_y B_y
$$

三次元ベクトルの場合：

$$
\mathbf{A} = (A_x, A_y, A_z)\\
\mathbf{B} = (B_x, B_y, B_z)
$$

$$
\mathbf{A} \cdot \mathbf{B} = A_x B_x + A_y B_y + A_z B_z
$$

内積の演算規則

交換法則（可換性）：

$$
\mathbf{A} \cdot \mathbf{B} = \mathbf{B} \cdot \mathbf{A}
$$

結合法則（スカラー倍との関係）：

スカラー $${k}$$ に対して、

$$
(k\mathbf{A}) \cdot \mathbf{B} = k(\mathbf{A} \cdot \mathbf{B}) = \mathbf{A} \cdot (k\mathbf{B})
$$

分配法則：

$$
\mathbf{A} \cdot (\mathbf{B} + \mathbf{C}) = \mathbf{A} \cdot \mathbf{B} + \mathbf{A} \cdot \mathbf{C}
$$

内積の非負性：

ベクトルの内積は次の性質を持ちます。

$$
\mathbf{A} \cdot \mathbf{A} = |\mathbf{A}|^2 \geq 0
$$

直交性の判定：

二つのベクトルが直交する（90度の角度をなす）ための必要十分条件は、

$$
\mathbf{A} \cdot \mathbf{B} = 0
$$

内積の計算例

例1：二次元ベクトルの内積

$$
\mathbf{A} = (3, 4)\\
\mathbf{B} = (2, 1)
$$

計算：

$$
\mathbf{A} \cdot \mathbf{B} = (3)(2) + (4)(1) = 6 4 = 2
$$

例2：三次元ベクトルの内積

$$
\mathbf{A} = (1, 0, 2)\\
\mathbf{B} = (4, 3, 1)
$$

計算：

$$
\mathbf{A} \cdot \mathbf{B} = (1)(4) + (0)(3) + (2)(1) = 4 + 0 2 = 2
$$

内積を用いた応用

二つのベクトル間の角度の計算：

内積の幾何学的定義を用いて、角度 $${\theta}$$ を求めることができます。

$$
\cos \theta = \dfrac{\mathbf{A} \cdot \mathbf{B}}{|\mathbf{A}|  |\mathbf{B}|}
$$

ベクトルの射影：

ベクトル $${\mathbf{A}}$$ をベクトル $${\mathbf{B}}$$ 上に射影した長さ $${proj_{\mathbf{B}} \mathbf{A}}$$ は、

$$
proj_{\mathbf{B}} \mathbf{A} = \dfrac{\mathbf{A} \cdot \mathbf{B}}{|\mathbf{B}|}
$$

物理学での仕事の計算：

力 $${\mathbf{F}}$$ が物体を変位 $${\Delta \mathbf{x}}$$ させるときの仕事 $${W}$$ は、

$$
W = \mathbf{F} \cdot \Delta \mathbf{x}
$$

長さと角度

内積の定義から見ましょう

$$
\bold a \cdot \bold b = |\bold a||\bold b|\cos\theta
$$

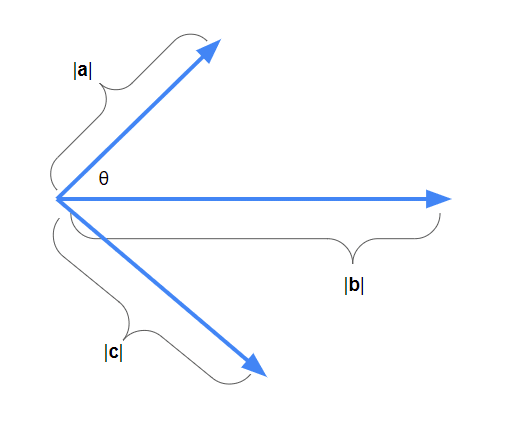
図で見ると

ここで$${|\bold a|}$$やら$${|\bold b|}$$やらはベクトルの長さ、大きさ、ノルムです。なのでこの定義による内積はベクトル２つの長さ（大きさ）とそのベクトルのなす角度という３つのパラメータで表されるスカラーです。

物理とかで出てくる内積は図の要領で、どっかしら向いてる力（ベクトルa)から特定方向（ベクトルb方向）にかかってる力を抜き出す時などに使われたりします。
特にベクトルbが単位ベクトル（長さ１）であったり、基底ベクトル（１番簡単なのはx軸、y軸、z軸に沿うベクトル）であったりする場合などによく使われます。この場合図の赤い矢印、いわゆる射影ベクトルが生成されます。

また、内積の対象となる２つのベクトルが共に単位ベクトルならば、その出力はそのまま$${cos \theta}$$です。これはプログラミングにおいてよく見られ、以下のような演算はそのまま２つのベクトルの成す角度をラジアンで返すことでしょう。

これは例えば面同士の単位法線に対して内積をとると、その曲がり具合が分かるといった具合です。

acos(Dot(n1,n2));
acos(Dot(v1.normalize(), v2.normalize()));

また比較の問題であるならば

ベクトルaとベクトルcのうち、どっちの方がベクトルbに力をかけているか、みたいな問題は内積の結果を比較すれば分かります。

成分同士の積の総和

内積にはもう１つ定義があり、ベクトルの成分同士の積の総和というやり方になります。

成分2つの2次ベクトルの内積

$$
\mathbf{a} \cdot \mathbf{b} = a_1 b_1 + a_2 b_2
$$

成分3つの3次ベクトルの内積

$$
\mathbf{a} \cdot \mathbf{b} = a_1 b_1 + a_2 b_2 + a_3 b_3
$$

成分n個のn次ベクトルの内積

$$
\mathbf{a} \cdot \mathbf{b} = \sum_{i=1}^{n} a_i b_i
$$

ベクトルの長さはベクトルの成分が決まれば計算できますので、先のベクトルの定義より、２つのベクトルの成分が決まればそれらの成す角度も求めることができます。

角度

$$
cos\theta=\frac{Dot(\bold{v}1,\bold{v}2)}{|\bold{v}1||\bold{v}2|}
$$

成分が決まれば、というのは、空間中の座標が決まっておれば、ということであり、空間中の点を操作してそこから長さなり角度なりを求めてというのはプログラミングの界隈ではよく使う操作であります。

前述の通り、単位ベクトル同士の内積はそのまま$${cos \theta}$$です。

位置と向き

内積の定義にコサインが含まれていることから、空間中の座標さえ分かっていれば、座標同士の位置関係をはかることができます。これは角度情報なしでコサインの機能を使用しているということです。

内積はコサインに対して、負値にはならないベクトルの長さという係数をかけますので、結果ベクトル同士の内積をとると

このような関係にあることが分かります。これは内積が２つの座標の位置関係（前か後か）、あるいは２つのベクトルの向き（同じ方向を向いている、真横を向いている、後ろを向いている）をはかることができることを示しています。

直交性

内積が０であるような関係を直交しているといいます。
幾何的に言うと直角を成しているベクトルです。
物理の例でいうならば、ある方向に力を及ぼそうとするベクトルがある時に、その力に加勢するでもなく、また阻害するでもない方向に向いているベクトルは直交しています。

直交していない物事は、他の直交している成分らの足し合わせによって表現することができたりします。例えば単純な２次元平面上の１点はｘ軸に沿ったベクトルとｙ軸に沿ったベクトルの足し合わせで表現できます。

直交している例
(25,4,0)と(0,0,80)

成分に０が含まれていると分かりやすいですが、成分に０がまったく含まれていなくても直交はします。
例えば２次元空間なら、あるベクトルに直交するベクトルは２つの方向に対して無数に定義できて、集めると直線を成します。

(-1,+1)と(-1,-1)は直交する
(-1,+1)と(+1,+1)は直交する
(-1,+1)と(+2,+2)は直交する
(-1,+1)と(+3,+3)は直交する
……以下無数

３次元空間なら、あるベクトルに直交するベクトルは面を成します。

これはまったく適当な例ですが、
例えばこの世界の【ミカン】なるものが『甘味』と『酸味』なる成分で構築されているとしたら、まったくそれらで構築されてなさそうな【プラッチック】は【ミカン】に対して直交しているといえます。

みかん（25,4,0)＝(甘味,酸味,プラッチックさ)
プラッチック(0,0,80)＝(甘味,酸味,プラッチックさ)
みかんとプラッチックの内積、すなわち成分同士の積の総和は０。ゆえにみかんとプラッチックは直交している。

この例は厳密でもなく適当でいい加減でろくでもないですが、
結局のところモデルの問題なので当てはめようと思ったらいくらでも当てはめることができるものです。

ひるがえって、あるものごとを構築していそうな成分を列挙して、それ以上分解できないような根本的な成分の並びが発見されたなら、それを基準として用いれば有用であるということが想像できます。そういう基準としてふさわしいなんらかのものを基底と言います。

先に少し述べた通り、根本的ななんらかの要素を係数倍して足し合わせれば、それらの要素からなるあまたのものごとが表現されうるからです。
そしてその、根本的な成分の組を生成するためには直交性を測ることが有用であるし、そのためにも内積は使えます。

この、これ以上分解できそうにない成分を空間の軸にとる時、それらの要素を基底といい、その要素がベクトルであるならば基底ベクトル、その要素が関数であるならば基底関数と呼ばれます。

そのちゃんとした定義は基底ベクトルの場合は線形独立であることとされるでしょう。ここで

$$
\sum\limits_{i=0}^N c_i \bm v_i=0
$$

を満たすのが、係数cが全部０の時しかないようなベクトルは線形独立。

すなわち矢印がちょっとでも伸びていて、それを足した時にゼロにする手段がないのが線形独立。足してゼロにできる関係にあるベクトルは線形独立でないなどとみなせます。

また、長さが０でないベクトルが互いに直交（内積ゼロ）ならばそれらのベクトルは線形独立です。証明はググったらでます。

基底関数の場合も、その選定には内積が利用され、内積の結果直交しているならば基底として利用できるという風になります。

線型方程式

変数の次数が１である

$$
\sum\limits_{i=0}^N a_ix_i
$$

のような多変数の関数は内積によって簡単に表現されます。

$$
\bm a \cdot \bm x = \sum\limits_{i=0}^N a_ix_i
$$

これを１行の行列と１列の行列の積であると考えるなら転置が必要です。

$$
\bm a \cdot \bm x^T
$$

変数の次数が１でない時はそれらは関数であると考えて

$$
a_0x^0+a_1x^1+a_2x^2+a_3x^3…= \sum\limits_{i=0}^N a_i f_i(x)
$$

みたいなこともできるでしょう。

スカラー積と内積

内積はベクトルの積なので方向情報が格納されます。
スカラー積は大きさだけです。

内積（ドット積）

内積は、二つのベクトルの間の角度や大きさに関する情報を統合し、結果としてスカラー量を得る演算です。ベクトル $${\mathbf{A}}$$ と $${\mathbf{B}}$$ の内積は次のように定義されます。

$$
\mathbf{A} \cdot \mathbf{B} = |\mathbf{A}| |\mathbf{B}| \cos\theta
$$

ここで、$${|\mathbf{A}|}$$ と $${|\mathbf{B}|}$$ はベクトルの大きさ（ノルム）、$${\theta}$$ は二つのベクトル間の角度です。内積は以下の特徴を持ちます。

二つのベクトルが同じ方向を向いているとき、内積は最大になります。
二つのベクトルが直交しているとき、内積はゼロになります。
内積は仕事やエネルギーの計算など、物理学において重要な役割を果たします。

仕事 $${W}$$ の計算

物理における仕事は、力と変位の内積として定義されます。

$$
W = \mathbf{F} \cdot \Delta \mathbf{x}
$$

これは、力 $${\mathbf{F}}$$ が変位 $${\Delta \mathbf{x}}$$ の方向にどれだけ作用したかを表しています。

スカラーの積

スカラーの積は、スカラー量とベクトルの積であり、結果はベクトルになります。スカラー $${k}$$ とベクトル $${\mathbf{A}}$$ のスカラーの積は次のように表されます。

$$
k \mathbf{A}
$$

この演算はベクトルの大きさをスカラー倍するだけで、方向は変わりません。

特定の方向を前提とした場合

力 $${F}$$ と変位 $${\Delta x}$$ をスカラー量とみなす場合、方向情報は考慮されませんが、力と変位が同じ直線上にある（例えば水平または垂直）と仮定できます。この場合、内積は単なるスカラーの積になります。

$$
W = F \Delta x
$$

これは、力が一定で変位と同じ方向に作用する場合に適用されます。

積分による一般化

力が位置によって変化する場合や、経路が曲線になる場合、仕事は積分を用いて計算します。

一次元の場合：

$$
W = \int_{x_1}^{x_2} F(x)  dx
$$

これは、力が変位に沿って変化する場合の仕事を計算するための積分で、線積分の特殊なケースです。

多次元の場合：

$$
W = \int_C \mathbf{F} \cdot d\mathbf{r}
$$

ここで、$${C}$$ は移動経路、$${d\mathbf{r}}$$ は微小な変位ベクトルです。この式は、任意の経路に沿って力が仕事をする場合の一般的な表現です。

グラムシュミット法

グラムシュミット法（GramSchmidt orthogonalization）は、線形代数における方法の一つで、与えられた線形独立なベクトルの集合を、互いに直交するベクトル（直交基底）に変換するアルゴリズムです。この方法により、ベクトル空間内で直交基底を構築できます。また、各ベクトルの大きさ（ノルム）を正規化すれば、直交基底を正規直交基底にすることもできます。

手順：

最初のベクトル $${ \mathbf{v}_1 }$$ をそのまま使い、そのノルムで割って正規化、つまり長さ１の単位ベクトルにします：

$$
\hat{\mathbf{u}_1} = \frac{\mathbf{v}_1}{|\mathbf{v}_1|}
$$

次に、次のベクトル $${ \mathbf{v}_2 }$$ から
$${ \mathbf{v}_2 }$$の$${ \mathbf{v}_1 }$$への正射影ベクトルを引き、
$${ \mathbf{v}_2 }$$の$${ \mathbf{v}_1 }$$に対する垂直射影ベクトルを出します。このベクトルは$${ \mathbf{v}_1 }$$に直交します。

$$
\mathbf{u}_2 = \mathbf{v}_2 - \text{proj}_{\mathbf{u}_1}(\mathbf{v}_2)
$$

ここで、$${ \text{proj}_{\mathbf{u}_1}(\mathbf{v}_2) }$$ は、$${ \mathbf{v}_2 }$$ の $${ \mathbf{u}_1 }$$ に対する射影ベクトルです。つまり向きは$${ \mathbf{v}_1 }$$および$${ \mathbf{u}_1 }$$で、大きさは$${ \mathbf{v}_2 }$$が$${ \mathbf{u}_1 }$$に落とした影の長さ分であるベクトルです。

正射影ベクトルは

$$
\text{proj}_{\mathbf{u}_1}(\mathbf{v}_2) = \frac{\mathbf{u}_1 \cdot \mathbf{v}_2}{\mathbf{u}_1 \cdot \mathbf{u}_1} \mathbf{u}_1
$$

これはつまり

$$
\text{projection}_{\bm a}(\bm b)
= \frac{\bm a}{|\bm a|} \frac{ |\bm{a}||\bm{b}|\cos \theta}{|\bm{a}|}
= \frac{\bm a}{|\bm a|} \frac{\bm a \cdot \bm b}{ |\bm a| }\\
= \bm a \frac{\bm a \cdot \bm b }{|\bm a ||\bm a |} = \bm a\frac{\bm{a} \cdot \bm{b}}{|\bm{a}|^2}\\
= \bm{a} \frac{ \bm a \cdot \bm b}{ \bm{a} \cdot \bm{a}}
$$

です。
これはつまり$${\bm b}$$の影を落とす先の軸が$${\bm a}$$であって、
その軸を伸び縮みさせる係数が$${ \frac{ |\bm{a}||\bm{b}|\cos \theta}{|\bm{a}|}}$$です。
結局形としては
落とされる先の軸の単位ベクトル$${\frac{\bm a}{|\bm a|}}$$と
落とした影の長さ$${ |\bm{b}|\cos \theta }$$の積

$$
\frac{\bm a}{|\bm a|} |\bm{b}|\cos \theta
$$

です。
特に落とす先の軸$${\bm a}$$が単位ベクトルなら

$$
\text{projection}_{\bm a}(\bm b)=\hat{\bm a}(\bm a \cdot \bm b)
$$

さて、$${\mathbf{v}_2}$$の$${\mathbf{v}_1}$$に対する垂直射影ベクトル

$$
\mathbf{u}_2 = \mathbf{v}_2 - \text{proj}_{\mathbf{u}_1}(\mathbf{v}_2)
$$

これを正規化して、次の正規化された長さ１の直交ベクトルを得ます。

$$
\hat{\mathbf{u}_2} = \frac{\mathbf{u}_2}{|\mathbf{u}_2|}
$$

同様に、次のベクトルも、これまでのすべての直交ベクトルに対して射影を取り、その成分を引くことで直交化します。例えば、$${ \mathbf{v}_3 }$$ に対しては：

$$
\mathbf{u}_3 = \mathbf{v}_3 - \text{proj}_{\mathbf{u}_1}(\mathbf{v}_3) - \text{proj}_{\mathbf{u}_2}(\mathbf{v}_3)
$$

これを正規化します。

$$
\hat{\mathbf{u}_3} = \frac{\mathbf{u}_3}{|\mathbf{u}_3|}
$$

これで少なくとも３次元なら正規直交基底が得られたことになります。

この手続きを繰り返すことで、元のベクトル集合から直交ベクトル集合が得られます。

例えばグラムシュミット法で、基底に掛かる係数を都合よくゼロにできればそれはある種の次元削減となります。ただし主成分分析などとは異なり、特に情報を持たない意味のない削減となります。