Octree色量子化
八分木による色量子化
1. 背景:
デジタル画像では色情報が豊富で、それをそのまま扱うとデータ量が非常に大きくなります。そこで、色の情報量を減少させつつ、できるだけ画像の見た目を保つための手法として色量子化が用いられることがあります。
2. 八分木の利用:
八分木は、空間を8等分するような木構造です。
2次元上の正方形を十字に切って小さな正方形に分割すると4つになりますが、3次元の立方体でそれをやると8つになります。
RGBは3つの成分を持ちますので、一種の3次元ベクトルとみなせます。八分木による色量子化は、3次元のRGB色空間を効率的に区分するために使われます。具体的には、RGBモデルの色成分(Red, Green, Blue)の各ビットを利用して、色空間を分割・代表する色を選出します。
3. 動作原理:
RGBモデルの各色には8ビットの情報があります。その最上位ビットから順に、八分木を構築していきます。
赤、緑、青の最上位ビットを組み合わせることで、$${2^3=8}$$の8通りの分岐が生まれます。この考え方を基に、八分木の各ノードで分岐を決定します。
次の分岐も同様に、次に大きいビットを基に決定します。
最上位ビット。左端。
most significant bitまたはhigh-order bit
最下位ビット。右端。
least significant bit
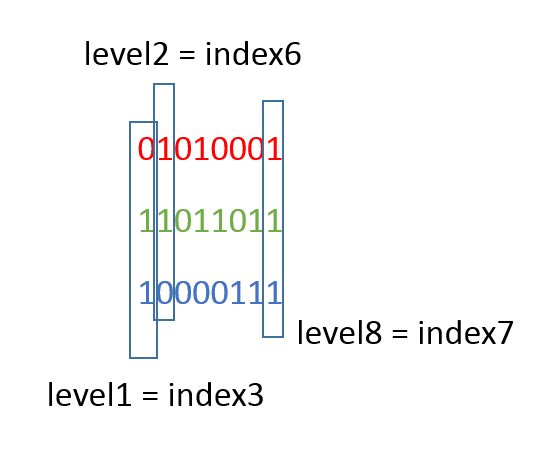
RGBの各成分が0-255の値で表されるなら、各々の成分は2進数で8bitである。RGB各成分から1bitずつ順番にとりだすと、これらは3bitで$${2^3=8}$$、すなわち0-7のインデックスとなる。この考えを元にするから八分木。つまり8つに分かれた。
4. 木構造の縮小:
メモリ効率の観点から、すべてのビットを用いて八分木を構築すると、莫大なデータ量となる可能性があるので、木の深さやノード数を制限することがあります。
最下位ビットは無視することで木のサイズを抑えることができます。
5. 色の代表化:
八分木の葉ノードには、特定の色範囲を代表する色が設定されます。
しかし、八分木の構築に使用するビット数や木の深さに制限を設けると、代表色が足りなくなることがあります。その際は、親ノードを葉ノードとして利用し、その色を代表色として使います。
6. 色の差異の調整:
木の深さが深いほど、色の差異が微細になるため、それを考慮して色情報を調整します。
必要な色数と現在の葉ノードの数を比較し、必要に応じてノードを結合して色情報を調整します。
この方法により、色のデータ量を効率的に減少させることができるため、ストレージや転送の効率を上げることができます。
RGB空間の量子化に用いられるOctreeの深さは最大で8ですか?
RGB空間の量子化に用いられるOctreeの深さが最大で8であるかという質問に対して、それはRGBのビット深度に依存します。典型的な24ビットRGB色空間では、各チャネル(R、G、B)は8ビットを持っており、それぞれのチャネルは0から255の256の異なる値を取ることができます。
Octreeの色量子化のコンセプトは、RGB空間を再帰的に8つのサブキューブに分割することに基づいています。最初の分割では、R、G、Bの各チャネルの中央値(127)を境にして空間を8分割します。次に、さらに細かく分割が行われる場合があります。
理論的には、各チャネルを完全に分解するためには、8レベルの深さ(8ビットの精度)が必要です。したがって、典型的な24ビットRGB空間の場合、Octreeの最大の深さは8になります。
しかし、実際の色量子化のアプリケーションでは、常に最大の深さまでOctreeを展開するわけではありません。ターゲットとする色の数や他の停止条件に達した場合に、早期に分割を停止することがよくあります。
32色の異なる色がOctreeに投入された場合、リーフの最大数は32ですか?
はい、32色の異なる色がOctreeに投入され、それぞれの色が異なる空間領域を占める場合、リーフノードの最大数は32になります。
Octreeは、色の空間を8つの子ノードに分割する再帰的なデータ構造です。新しい色が追加されるたびに、その色が所属する領域を示すパスに従ってOctreeを進み、リーフノードが作成または更新されます。
32色がそれぞれ異なる領域にある場合、それぞれの色には独自のリーフノードが対応します。したがって、32の異なる色がOctreeに追加されると、リーフノードの最大数は32になります。
ただし、実際の応用や状況によっては、32色が同じリーフノードにマッピングされる可能性も考えられます。例えば、Octreeの深さに制限を設けたり、ある深さを超えて分割しないようにした場合などです。その場合、リーフノードの数は32未満になることもあり得ます。
まとめ
Octreeに投入された色はノードによって分岐、あるいは集計され、木の末端であるリーフを目指す。理論上、木が最大まで成長するのであれば、リーフは投入された色を一意に識別する。すなわち、RGBの各成分が$${8bit=2^8=256}$$であるならば、最大まで成長したリーフの個数は$${256^3}$$である。
Octreeで色を削減する、とは。このような木構造の成長を途中で打ち切ったり、条件によってリーフを削除し、新たな色のセットを作成することである。
ソース
OctreeNode
class OctreeNode {
constructor(level = 0, parent = null) {
this.color = [0, 0, 0];
this.pixelCount = 0;
this.children = new Array(8);
this.level = level;
this.parent = parent;
}
// isLeaf() {
// return !this.children.some(child => child !== undefined);
// }
isLeaf() {
return !this.hasChild();
}
hasChild() {
return this.children.some(child => child !== undefined);
}
getLeafNodes(nodes = []) {
if (this.isLeaf()) {
nodes.push(this);
} else {
this.children.forEach(child => {
if (child) child.getLeafNodes(nodes);
});
}
return nodes;
}
addColor(color, level) {
//node通過時に色情報を集計する場合
//ただしreduce, merge時に集計するなら不要
// this.color[0] += color[0];
// this.color[1] += color[1];
// this.color[2] += color[2];
// this.pixelCount++;
if (level === 8) {
this.color[0] += color[0];
this.color[1] += color[1];
this.color[2] += color[2];
this.pixelCount++;
return;
}
const index = this._getOctreeIndex(color, level);
if (!this.children[index]) {
this.children[index] = new OctreeNode(level + 1, this);
}
this.children[index].addColor(color, level + 1);
}
reduce(method = 'shallowest') {
if (method === 'shallowest') {
this._reduceByShallowestLeaf();
}
if (method === 'deepest') {
this._reduceByDeepestLeaf();
} else if (method === 'leastColor') {
this._reduceByLeastColor();
}
}
//浅い方を刈る=色は集約される
_reduceByShallowestLeaf() {
const leafNodes = this.getLeafNodes();
let minLevel = Infinity;
let shallowestNode = null;
leafNodes.forEach(node => {
if (node.level < minLevel) {
minLevel = node.level;
shallowestNode = node;
}
});
this._mergeNodeToParent(shallowestNode);
}
//深い方を刈る=色はまんべんなく残る
_reduceByDeepestLeaf() {
const leafNodes = this.getLeafNodes();
let maxLevel = -1;
let deepestNode = null;
leafNodes.forEach(node => {
if (node.level > maxLevel) {
maxLevel = node.level;
deepestNode = node;
}
});
this._mergeNodeToParent(deepestNode);
}
//使用回数の少ない色を刈る
_reduceByLeastColor() {
const leafNodes = this.getLeafNodes();
let minPixelCount = Infinity;
let leastColorNode = null;
leafNodes.forEach(node => {
if (node.pixelCount < minPixelCount) {
minPixelCount = node.pixelCount;
leastColorNode = node;
}
});
this._mergeNodeToParent(leastColorNode);
}
_mergeNodeToParent(node) {
if (node && node.parent) {
const parent = node.parent;
parent.color[0] += node.color[0];
parent.color[1] += node.color[1];
parent.color[2] += node.color[2];
parent.pixelCount += node.pixelCount;
for (let i = 0; i < 8; i++) {
if (parent.children[i] === node) {
parent.children[i] = undefined;
}
}
}
}
_getOctreeIndex(color, level) {
let index = 0;
const mask = 0x80 >> level;
if (color[0] & mask) index |= 4;
if (color[1] & mask) index |= 2;
if (color[2] & mask) index |= 1;
return index;
}
}量子化実行
function quantizeWithOctree(imageData, colorCount) {
const root = new OctreeNode();
//Octree構築工程
for (let i = 0; i < imageData.data.length; i += 4) {
const color = [imageData.data[i], imageData.data[i + 1], imageData.data[i + 2]];
root.addColor(color, 0);
}
let leaves = root.getLeafNodes();
if (leaves.length === 0) return imageData; // 何もしない
//リーフ削減工程
let maxAttempts = 1000;
let attempts = 0;
while (leaves.length > colorCount && attempts < maxAttempts) {
leaves = root.getLeafNodes();
for (let leaf of leaves) {
if (leaf.parent) {
leaf.parent.reduce();
}
}
attempts++;
}
// 試行回数の上限に達してもリーフノードの数がcolorCountを超えている場合
if (leaves.length > colorCount) {
// leavesを先頭からcolorCountの数だけ取得
//console.log("count over");
leaves = leaves.slice(0, colorCount);
}
//この段階ではnodeのColor値は下位のノードの累積
// for (let i = 0; i < leaves.length; i++) {
// console.log(leaves[i].color);
// console.log(leaves[i].pixelCount);
// }
//nodeの代表色を作成、ここでは平均化処理
const palette = leaves.map(leaf => {
return leaf.color.map(value => Math.round(value / leaf.pixelCount));
});
//パレットの適用
for (let i = 0; i < imageData.data.length; i += 4) {
const color = [imageData.data[i], imageData.data[i + 1], imageData.data[i + 2]];
const closest = palette.reduce((acc, paletteColor) => {
const dist1 = colorDistance(color, acc);
const dist2 = colorDistance(color, paletteColor);
return dist1 < dist2 ? acc : paletteColor;
}, palette[0]); // 初期値を追加
imageData.data[i] = closest[0];
imageData.data[i + 1] = closest[1];
imageData.data[i + 2] = closest[2];
}
return imageData;
}Octreeの構築
1.オクトリーの構築:
画像内の各ピクセルの色をオクトリーに追加する。
2進数RGB値の各桁から取得したインデックス(1成分1bit, RGB3成分で3bit=$${2^3}$$, 0-7のインデックス)を利用して、各色を8階層(ルート入れると9階層, これは色の成分が8bit=0-255を想定しているからであって、この色深度がもっと深ければオクトリーも深い)のオクトリーの適切な位置に配置する。
const root = new OctreeNode();
for (let i = 0; i < imageData.data.length; i += 4) {
const color = [imageData.data[i], imageData.data[i + 1], imageData.data[i + 2]];
root.addColor(color, 0);
}2.色の分布と集計:
オクトリーの各ノードは、そのノードを通過した色の合計と色の数(ピクセル数)を保持する。ただしノード削減時に集計するなら追加時にカウントする必要はない。
addColor(color, level) {
//node通過時に色情報を集計する場合
//ただしreduce, merge時に集計するなら不要
// this.color[0] += color[0];
// this.color[1] += color[1];
// this.color[2] += color[2];
// this.pixelCount++;
if (level === 8) {
this.color[0] += color[0];
this.color[1] += color[1];
this.color[2] += color[2];
this.pixelCount++;
return;
}
const index = this._getOctreeIndex(color, level);
if (!this.children[index]) {
this.children[index] = new OctreeNode(level + 1, this);
}
this.children[index].addColor(color, level + 1);
}ノードの分岐とインデックス
_getOctreeIndex(color, level) {
let index = 0;
const mask = 0x80 >> level;
if (color[0] & mask) index |= 4;
if (color[1] & mask) index |= 2;
if (color[2] & mask) index |= 1;
return index;
}_getOctreeIndexにより、
入力されたRGB($${256^3}$$)に対してオクトリーが8階層成長するのであれば、全ての色は必ず一意のインデックスを得る$${256^3=8^8=16777216}$$。
初期化: index変数を0に初期化します。このindexは、0から7までの整数として、子ノードの場所を示します。
マスクの作成: mask変数には、現在のレベルに応じたビットマスクが格納されます。レベル0では、maskは0x80(バイナリで10000000)、レベル1では0x40(バイナリで01000000)、というようになります。
RGB値の各チャンネルに対してビットテストを実施:
if (color[0] & mask) index |= 4;: これは、Rチャンネルの値(color[0])の現在のレベルのビットが1であるかどうかを確認します。もし1であれば、indexの3番目のビットをセットします(4=バイナリで100)。
if (color[1] & mask) index |= 2;: これは、Gチャンネルに対して同様の確認を行い、indexの2番目のビットをセットします。(2=バイナリで10)。
if (color[2] & mask) index |= 1;: これは、Bチャンネルに対して同様の確認を行い、indexの1番目のビットをセットします。
color[]の各々の値はR,G,Bの0-255,
二進数だと各々8桁。
例えば、RGB色が(150, 50, 200)でレベルが1の場合、
Rチャンネルの値150はバイナリで10010110、
Gチャンネルの値50は00110010、
Bチャンネルの値200は11001000。
レベル1のmaskは0x40、つまり01000000です。RとBチャンネルの該当するビットが1ですが、Gチャンネルのものは0です。この結果、計算されるインデックスは101、つまり5になります。
この方法により、RGBの3チャンネルそれぞれの値に基づいて、0から7の範囲で子ノードのインデックスを計算することができます。
3.リーフノードの取得:
オクトリーのすべてのリーフノード(子ノードを持たないノード)を取得する。
const leaves = root.getLeafNodes(); getLeafNodes(nodes = []) {
if (this.isLeaf()) {
nodes.push(this);
} else {
this.children.forEach(child => {
if (child) child.getLeafNodes(nodes);
});
}
return nodes;
}このメソッドは深さ優先探索(DFS: Depth-First Search)
isLeafの実装は以下
isLeaf() {
return !this.children.some(child => child !== undefined);
} some
配列の要素のいずれかが真ならばtrue
全ての要素が偽ならfalseを返す。
これは以下のように書き換えられる。
isLeaf() {
return !this.hasChild();
}
hasChild(){
return this.children.some(child => child !== undefined);
}4.色の数の削減:
指定された試行数、および色の数に達するまで、リーフノードの一部を結合(削減)する。
最も似ている色や最も少ないピクセルを持つノードから結合を始めるのが一般的。
//リーフ削減工程
let maxAttempts = 1000;
let attempts = 0;
while (leaves.length > colorCount && attempts < maxAttempts) {
leaves = root.getLeafNodes();
for (let leaf of leaves) {
if (leaf.parent) {
leaf.parent.reduce();
}
}
attempts++;
}削減手法(ただし16色とかに絞る場合、そんなに違いは出ないと思われる)
reduce(method = 'shallowest') {
if (method === 'shallowest') {
this._reduceByShallowestLeaf();
}
if (method === 'deepest') {
this._reduceByDeepestLeaf();
} else if (method === 'leastColor') {
this._reduceByLeastColor();
}
}
//浅い方を刈る=色は集約される
_reduceByShallowestLeaf() {
const leafNodes = this.getLeafNodes();
let minLevel = Infinity;
let shallowestNode = null;
leafNodes.forEach(node => {
if (node.level < minLevel) {
minLevel = node.level;
shallowestNode = node;
}
});
this._mergeNodeToParent(shallowestNode);
}
//深い方を刈る=色はまんべんなく残る
_reduceByDeepestLeaf() {
const leafNodes = this.getLeafNodes();
let maxLevel = -1;
let deepestNode = null;
leafNodes.forEach(node => {
if (node.level > maxLevel) {
maxLevel = node.level;
deepestNode = node;
}
});
this._mergeNodeToParent(deepestNode);
}
//使用回数の少ない色を刈る
_reduceByLeastColor() {
const leafNodes = this.getLeafNodes();
let minPixelCount = Infinity;
let leastColorNode = null;
leafNodes.forEach(node => {
if (node.pixelCount < minPixelCount) {
minPixelCount = node.pixelCount;
leastColorNode = node;
}
});
this._mergeNodeToParent(leastColorNode);
}
_mergeNodeToParent(node) {
if (node && node.parent) {
const parent = node.parent;
parent.color[0] += node.color[0];
parent.color[1] += node.color[1];
parent.color[2] += node.color[2];
parent.pixelCount += node.pixelCount;
for (let i = 0; i < 8; i++) {
if (parent.children[i] === node) {
parent.children[i] = undefined;
}
}
}
}5.新しいパレットの作成:
削減後のリーフノードから、新しい色のパレットを作成する。
各リーフノードの平均色が、新しいパレットの色として使用される。
//nodeの代表色を作成、ここでは平均化処理
const palette = leaves.map(leaf => {
return leaf.color.map(value => Math.round(value / leaf.pixelCount));
});6.画像の再構築:
元の画像の各ピクセルに対して、新しいパレットの中で最も近い色を探す。
色の近さは、通常、RGB空間でのユークリッド距離を使用して計算される。
各ピクセルの色を、その最も近い色に置き換える。
for (let i = 0; i < imageData.data.length; i += 4) {
const color = [imageData.data[i], imageData.data[i + 1], imageData.data[i + 2]];
const closest = palette.reduce((acc, paletteColor) => {
const dist1 = colorDistance(color, acc);
const dist2 = colorDistance(color, paletteColor);
return dist1 < dist2 ? acc : paletteColor;
}, palette[0]); // 初期値を追加
imageData.data[i] = closest[0];
imageData.data[i + 1] = closest[1];
imageData.data[i + 2] = closest[2];
}acc は、多くの文脈で "accumulator"(アキュムレータ)の略として使用されます。JavaScriptの reduce メソッドのコールバック関数の第一引数としてしばしば使用されます。この引数は、前の呼び出しからの結果を保持し、次の呼び出しで使用されます。
以下は、reduce メソッドを使って配列の要素を合計する簡単な例です。
const numbers = [1, 2, 3, 4, 5];
const sum = numbers.reduce((acc, curr) => acc + curr, 0);
console.log(sum); // 15
この例では、accは累積値を保持し、currは現在の配列の要素を指します。reduce メソッドは配列の各要素に対してコールバック関数を実行し、結果を acc に累積していきます。最後に、累積された結果(この場合は合計)が返されます。
7.結果の返却:
減色された新しい画像や、新しい色のパレットを結果として返す。
このプロセスにより、画像の色数が効果的に削減され、特定の色数に制限されたパレットを持つ新しい画像が生成されます。
