最小二乗法

重回帰、および行列形の正規方程式はこちら。

はじめに

まず金谷先生の本を買います。

これなら分かる応用数学教室―最小二乗法からウェーブレットまで 単行本 – 2003/6/1金谷 健一 (著)

適当なN個のデータ点が観測されたとして
それらになんらかの関数をあてはめたい。
なぜならば一度適切な関数を得ることができたならば、次からは新たなデータを改めて観測することなくだいたいこんなもんだと予測できるからである。

なんらかの関数を得る方法はいろいろあって、得られたデータ点を通過するような関数を得ることを補間といい、データ点を総じて見た時それっぽいところを通るような関数を得ることを回帰という。ただしどっちがどっちでなければならない的な厳密なものではない。最終的に必要な関数を得るという意味では同じだからである。

回帰

補間

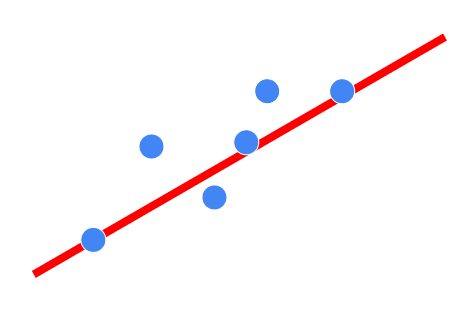
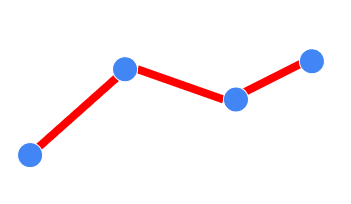
基本的に、関数を曲げようとすると関数の次数があがる。

１回曲がると２次の関数
２回曲がると３次の関数

次数が上がり過ぎると往々にしてロクなことがないので、次数はそれなりにして、あとは関数同士を滑らかに接続することを考えるとスプラインと呼ばれる分野となる。これはどちらかというと補間の文脈となる。

補間やらなんやらはこちら

線形回帰

最小二乗法は回帰の文脈、統計の文脈でしばしば現れる。

そのおおまかなやり方は
観測されたデータ点と、得るべき関数との誤差を示す関数を立て、その誤差関数を最小にするように得るべき関数の未知の係数を決定することである。

例えばデータ点に直線をあてはめたいと考えた時

回帰

このあてはめたい直線が

$$
y=ax+b
$$

という形をしているとする。

この直線の方程式は直線という形状は分かるが、係数a,bが未知なので完全ではない。最小二乗法は、このような未知なる係数を決定することによって、あてはめたい関数を完成させることを目指す。

直線の方程式の場合$${y-(ax+b)}$$がイコール0ならばxに応じたyは直線上にあることを意味する。逆に0でないならばyは直線からずれている。このずれを偏差という。

偏差という語はなんかの値からのズレという程度の意味合いでしかないが、文脈によっては期待値からのズレなどと意味が固定されていることがある。今回は関数からのズレを偏差と呼ぶ。

与えられた全ての観測値、データ点において、あてはめたい関数との偏差を最小にすることを考えると

$$
J=\frac{1}{2}\sum\limits_{i=1}^{N}(y_i-(ax_i+b))^2 \to min
$$

なる式が立つ。$${y_i-(ax_i+b)}$$は個々のデータ点と関数との偏差。$${x_i,y_i}$$には実際に観測されたデータ点として具体的な数値が入力される。データ点はここではN個。

二乗しているのは絶対値的な意味合い。すなわち今知りたいのは与えられた関数からのデータ点の離れ具合であって、+1と-1はズレとしては同じ1である。これらのズレはそのまま総和をとると互いに打ち消しあってズレとしての意味を失う（本来ならばデータ点が+1と-1でズレているなら、ズレの総和は2つ分くらいに換算してほしいのである）。二乗することにより、どれくらいズレているのかの意味を保ったまま総和をとることができる。すなわち絶対値的な意味の二乗である。絶対値を使用しないのは微分を用いた計算の簡便さのためであり、1/2が付いてるのもそのためである。

最小にするという制限は、他と比較して小さければ要件を成す。具体的な数値はあんまり関係がない。ある関数が極値（最小値ないし最大値）をとるためには微分値が０である必要があって、誤差関数は誤差が積み重なるように作ってあるから下に凸。よくよく見ると$${f(x)=x^2}$$と同じ形してるから下に凸。誤差は０が最小で、また、誤差は負にはならぬ。誤差が０の時、発見された直線は全てのデータ点を直線上に持つ。ちょっとでも直線からズレたデータ点があるなら、誤差関数は０にはならぬ。が、なんらかの最小値は持つ。

微分値が０ならその時がその関数が最小値をとる時である。具体的な最小値がなんなのかはあんまり関係ない。０かもしれないし０じゃないかもしれない。０ならば全てのデータ点が関数上にある。

$$
\frac{\partial J}{\partial a}=0,\quad \frac{\partial J}{\partial b}=0
$$

これが未知なる係数a,bを求めるための連立方程式となる。実際に偏微分を誤差関数に適用すると

$${(y_i-(ax_i+b))^2}$$の部分は合成関数の微分を適用

$$
合成関数の微分\\
{f(g(x))}'=f'(g(x))g'(x)=f'(t)g'(x)
$$

ここで
$${f(x)=\lbrace g(x)\rbrace^2=t^2}$$
$${f'(x)=2(y_i-(ax_i+b))=2t}$$
$${g(x)=(y_i-(ax_i+b))=t}$$
$${g'(x)=-x \quad aの偏微分の場合}$$
$${g'(x)=-1 \quad bの偏微分の場合}$$

$$
\frac{\partial J}{\partial a}=\sum\limits_{i=1}^{N}(y_i-ax_i-b)(-x_i)=a\sum\limits_{i=1}^{N}x_i^2+b\sum\limits_{i=1}^{N}x_i-\sum\limits_{i=1}^{N}x_iy_i=0
$$

$$
\frac{\partial J}{\partial b}=\sum\limits_{i=1}^{N}(y_i-ax_i-b)(-1)=a\sum\limits_{i=1}^{N}x_i+b\sum\limits_{i=1}^{N}1-\sum\limits_{i=1}^{N}y_i=0
$$

正規方程式

行列形式にすると

$$
\begin{pmatrix}
\sum\limits_{i=1}^{N}x_i^2 & \sum\limits_{i=1}^{N}x_i \\
\sum\limits_{i=1}^{N}x_i & \sum\limits_{i=1}^{N}1 \\
\end{pmatrix}
\begin{pmatrix}
a \\
b  \\
\end{pmatrix}
=
\begin{pmatrix}
\sum\limits_{i=1}^{N}x_iy_i \\
\sum\limits_{i=1}^{N}y_i \\
\end{pmatrix}
$$

プログラム的には(processingで書いてます）

double[] LeastSquareLiner(List<PVector> vertices)
{
  double n = 0;
  double xx_sum = 0;
  double x_sum = 0;
  double xy_sum = 0;
  double y_sum = 0;
  
  for(var v : vertices)
  {
    n++;
    xx_sum+=v.x*v.x;
    x_sum+=v.x;
    xy_sum+=v.x*v.y;
    y_sum+=v.y;
  }
  
  double[][] A = {{xx_sum,x_sum},{x_sum,n}};
  double[] b = {xy_sum,y_sum};
  var x = MatrixMethod.CramersRules(A,b);
  
  return x;
}

連立方程式が２つなのでクラメルの公式で力付くでといてある。

クラメルの公式はこちら

リンク先はC#で書いてあるのでちょっとなおす必要がある。
しかし、連立方程式がたかだか２つや３つの時は比較的簡単な計算で済むため、『最小二乗法、プログラム』などで検索するとMatrixMethod.CramersRules(A,b);の部分をそのまま計算式にした実装がいっぱいでてくるのでそれらをもちいることができる。

そのた行列一般

テスト用コピペ用プログラム

processingで遊びたい場合は以下をコピペすることができる。
このテストプログラムは、原点を画面の中央に持ってきていることに注意を要する。ピクセル座標をそのまま使うと、座標値が全部プラスになって傾きが大して変わらないおもんない直線になるからである。

そのため、画面上に存在する円の座標(x+,y+)に対して、原点ベクトル（ここでは画面中央）を用意し、円の座標マイナスすることの原点ベクトルとすることで計算用の座標を作り出している。この計算用の座標は最小二乗法にほりこまれ、あてはめたい関数の係数を形成する。

関数が完成したらあとは好きなxを当てはめてよい。しかし画面上に存在する表示円に対して適用されているように見せたいのなら、表示円に対して存在する原点ベクトルを意識する必要がある。今、原点ベクトルは画面中央であるから、画面左端に相当するstart_xは-width/2となる。

これを一般化して、原点ベクトルを画面中央に限らないとするなら、
start_xは-origin.x（画面左端に相当するx）
end_xはwidth-origin.x（画面右端に相当するx）となる。

あとはstart_xからend_xまで、
線形回帰なら２点に応じたyを出力
曲線あてはめなら定点でxを刻んで、それに応じたyを得る。

得られたx,yを表示するには原点ベクトルをプラスする。

import java.util.Collections;//Convex用
import java.util.Comparator;//Convex用
import java.util.ArrayDeque;//Countour用
import java.util.Deque;//Countour用
import java.util.Queue;//Countour用
import java.util.Stack;//Countour用

import java.util.Arrays;
import java.util.List;
import java.util.Collection;
import java.util.stream.Stream;
import java.util.stream.Collectors;


void setup()
{
  size(500,500);
  background(255);
  origin = new PVector(250,250);
  Vertices = MakeRandomDots(10,0,500);
}

  //画面の中央を原点にしないと全部のx,yがプラスになって
  //回帰した線が同じ方向向く
PVector origin;
List<PVector> Vertices = new ArrayList<PVector>();
float Vertices_r = 20;

List<PVector> MakeRandomDots(int n, float min, float max)
{
  List<PVector> ret = new ArrayList<PVector>();
  for(int i = 0; i<n; i++)
  {
    ret.add(new PVector(random(min,max),random(min,max)));
  }
  return ret;
}
void DrawDots(List<PVector> dots, float r)
{
  for(var v : dots)
  {
    circle(v.x,v.y,r);
  }
}


void draw()
{
  background(255);
 
  List<PVector> input = new ArrayList<PVector>();
  for(var v : this.Vertices)
  {
    input.add(v.copy().sub(origin));
  } 
  var x = LeastSquareLiner(input);
  
  
  if(x==null||x.length<2){return;}
  float a = (float)x[0];
  float b = (float)x[1];
  //float sy = b;
  //float ey = a*width+b;
  float sy2 = a*(-width/2)+b;   
  float ey2 = a*(width/2)+b;
     
  fill(0);
  line(0,origin.y+sy2,width,origin.y+ey2);
  
  DrawDots(this.Vertices,Vertices_r);
  
}

//Event_GUI
PVector _press_pos;
PVector _release_pos;
PVector _pprev;
PVector _prev;
PVector _current;
PVector _dv = new PVector(0,0);
int current_vertex_index = -1;
int current_gui_index = -1;

void mousePressed()
{ 
  _press_pos = new PVector(mouseX,mouseY);
  _pprev = new PVector(mouseX,mouseY);
  _prev = new PVector(mouseX,mouseY);
  _current = new PVector(mouseX,mouseY);    
  
  //Vertices
  for(int i = 0; i<this.Vertices.size(); i++)
  {
    if(PointInCircle(this.Vertices.get(i),this.Vertices_r,new PVector(mouseX,mouseY)))
    {
       current_vertex_index = i;        
    }
  }    
}

//円周上を含まないPointIn
static boolean PointInCircle(PVector center, float radius, PVector v)
{
  float dx = v.x-center.x;
  float dy = v.y-center.y;
  if(dx*dx+dy*dy<radius*radius){return true;}
  return false;
}

void mouseDragged()
{
  if(_current==null){return;}
  if(_prev!=null){_pprev = _prev.copy();}
  
  _prev = _current.copy();
  _current.x = mouseX;
  _current.y = mouseY;  
  _dv = PVector.sub(_current,_prev);
  
  //Vertices
  if(0<=current_vertex_index)
  {
    for(int i = 0; i<this.Vertices.size(); i++)
    {
      this.Vertices.get(current_vertex_index).x = mouseX;
      this.Vertices.get(current_vertex_index).y = mouseY;    
    }    
  }   
}

void mouseReleased()
{
  _release_pos = new PVector(mouseX,mouseY);    
  _pprev = null;
  _prev = null;
  _current = null;  
  current_vertex_index=-1;
  current_gui_index=-1;  
}

//↑Event
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////

static class MatrixMethod
{
  
  //転置
  public static double[][] Transpose(double[][] matrix)
  {
      int row_count = matrix.length;
      int col_count = matrix[0].length;

      //反転
      double[][] ret = new double[col_count][row_count];

      for (int row_index = 0; row_index < row_count; row_index++)
      {
          for (int col_index = 0; col_index < col_count; col_index++)
          {
              ret[col_index][row_index] = matrix[row_index][col_index];
          }
      }
      return ret;
  }

   //行列式略記
   static double Det(double[][] matrix)
   {
       return DeterminantN(matrix);
   }
   
   static double DeterminantN(double[][] matrix)
   {
       int m = matrix.length;
       int n = matrix[0].length;

       if (m != n) { throw new IllegalArgumentException(); }
       else if (m == 1) { return matrix[0][0]; }
       else if (m == 2) { return Determinant2(matrix); }
       else if (m == 3) { return Determinant3(matrix); }
       else { return CofactorExpansion(matrix); }
   }
   
   //行列式
   static double Determinant2(double[][] m)
   {
       //二次の場合
       //|a b|
       //|c d|
       var a = m[0][0];
       var b = m[0][1];
       var c = m[1][0];
       var d = m[1][1];
       return a * d - b * c;
   }
   
   static double Determinant2(
       double a, double b,
       double c, double d)
   {
       //二次の場合
       //|a b|
       //|c d|
       return a * d - b * c;
   }
   
   static double Determinant3(double[][] m)
   {
       //三次の場合
       //|a b c|
       //|d e f|
       //|g h i|

       var a = m[0][0];
       var b = m[0][1];
       var c = m[0][2];

       var d = m[1][0];
       var e = m[1][1];
       var f = m[1][2];

       var g = m[2][0];
       var h = m[2][1];
       var i = m[2][2];

       return a * Determinant2(e, f, h, i) - d * Determinant2(b, c, h, i) + g * Determinant2(b, c, e, f);
   }
   
   static double Determinant3(
       double a, double b, double c,
       double d, double e, double f,
       double g, double h, double i)
   {
       //三次の場合
       //|a b c|
       //|d e f|
       //|g h i|
       return a * Determinant2(e, f, h, i) - d * Determinant2(b, c, h, i) + g * Determinant2(b, c, e, f);
   }

   //余因子を取得する
   static double CalcuCofactor(double[][] matrix, int input_row_index, int input_col_index)
   {
       return _sign(input_row_index + input_col_index) * Det(GetMinorMatrix(matrix, input_row_index, input_col_index));
   }
   
   //符号
   static int _sign(int value)
   {
       if (value % 2 == 0){return 1;}//偶数
       else{return -1;}//奇数
   }   
      
   //余因子展開
   static double CofactorExpansion(double[][] matrix)
   {
       //ループはどこかの１列、あるいは１行のみ行えばよい
       //どの行、列を選択しても結果は同じとなる            
       int col_index = 0;
       int row_count = matrix.length;
       //int col_count = matrix.GetLength(1);
       double ret = 0;
       for (int row_index = 0; row_index < row_count; row_index++)
       {
           ret += matrix[row_index][col_index] * CalcuCofactor(matrix, row_index, col_index);
       }
       return ret;
   }
      
  //要素が余因子である行列
  //余因子行列はこれを転置したもの
  public double[][] CofactorMatrix(double[][] matrix)
  {
      int row_count = matrix.length;
      int col_count = matrix[0].length;

      double[][] ret = new double[row_count][col_count];

      for (int row_index = 0; row_index < row_count; row_index++)
      {
          for (int col_index = 0; col_index < col_count; col_index++)
          {
              ret[row_index][col_index] = CalcuCofactor(matrix, row_index, col_index);
          }
      }
      return ret;
  }   
 
   //小行列を取得する(略記）
   static double[][] M(double[][] matrix, int i, int j)
   {
       return GetMinorMatrix(matrix, i, j);
   }
   
   //小行列を取得する
   static double[][] GetMinorMatrix(double[][] matrix, int input_row_index, int input_col_index)
   {
       int row_count = matrix.length;//row_count, 行数
       int col_count = matrix[0].length;//col_count, 列数
       if (row_count != col_count) { return null; }
       int ret_row_index = 0;
       int ret_col_index = 0;
       double[][] ret = new double[row_count - 1][col_count - 1];
       for (int r = 0; r < row_count; r++)
       {
           if (r == input_row_index) { continue; }
           for (int c = 0; c < col_count; c++)
           {
               if (c == input_col_index) { continue; }
               ret[ret_row_index][ret_col_index] = matrix[r][c];
               ret_col_index++;
           }
           ret_col_index = 0;
           ret_row_index++;
       }
       return ret;
   }



  //随伴行列、余因子行列
  //要素を余因子とした行列の転置
  public double[][] AdjugateMatrix(double[][] matrix)
  {
      //転置
      return Transpose(CofactorMatrix(matrix));
  }

  //余因子行列を用いた逆行列
  public double[][] InverseMatrixFromCofactor(double[][] matrix)
  {
      return Divide(AdjugateMatrix(matrix), Det(matrix));
  }

  //クラメルの公式
  static double[] CramersRules(double[][] A, double[] x, double[] b)
   {
       double[] ret = new double[x.length];
       for (int x_index = 0; x_index < x.length; x_index++)
       {
           ret[x_index] = CramersRule(A, x_index, b);
       }
       return ret;
   }
   
   static double[] CramersRules(double[][] A, double[] b)
   {
       double[] ret = new double[b.length];
       for (int x_index = 0; x_index < b.length; x_index++)
       {
           ret[x_index] = CramersRule(A, x_index, b);
       }
       return ret;
   }
       
   //クラメルの公式要素１つ分
   static double CramersRule(double[][] A, int x_index, double[] b)
   {
       var Ai = PasteCol(A, x_index, b);
       return Det(Ai) / Det(A);
   }  


  //行貼り付け
  //newして戻り値返すタイプ
  //機能的にはSetと変わらない
  public static double[][] PasteRow(double[][] matrix, int row_index, double[] new_row)
  {
      int row_count = matrix.length;
      int col_count = matrix[0].length;                       
      double[][] ret = new double[row_count][col_count];
      
      for(int i = 0; i<row_count; i++)
      {
        for (int j = 0; j < col_count; j++)
        {
          if(i==row_index)
          {
            //入力配列が短い場合は0で埋める
            //必然的に、長い場合は切り落とされる
            if (new_row.length - 1 < j)
            {
                ret[row_index][j] = 0;
            }
            ret[row_index][j] = new_row[j];
          }
          else
          {
            ret[i][j]=matrix[i][j];
          }         
        }
      }
      return ret;
  }
  //列貼り付け
  public static double[][] PasteCol(double[][] matrix, int col_index, double[] new_col)
  {
      int row_count = matrix.length;
      int col_count = matrix[0].length;    
      double[][] ret = new double[row_count][col_count];
      
      for (int i = 0; i < row_count; i++)
      {
        for(int j = 0; j < col_count; j++)
        {
          //貼り付け列
          if(j==col_index)
          {
            //入力配列が短い場合は0で埋める
            //必然的に、長い場合は切り落とされる
            if (new_col.length - 1 < i)
            {
                ret[i][col_index] = 0;
            }            
            ret[i][col_index] = new_col[i];
          }
          else
          {
            ret[i][j]=matrix[i][j];
          }
        }
      }
      return ret;
  }
  
  public static double[][] AddRow(double[][] matrix, double[] new_row)
  {
      int row_count = matrix.length;
      int col_count = matrix[0].length;  
      double[][] ret = new double[row_count + 1][col_count];
      for (int row_index = 0; row_index < row_count + 1; row_index++)
      {
          for (int col_index = 0; col_index < col_count; col_index++)
          {
              //最後の追加行
              if (row_index == row_count)
              {
                  ret[row_index][col_index] = new_row[col_index];
              }
              else
              {
                  ret[row_index][col_index] = matrix[row_index][col_index];
              }
          }
      }
      return ret;
  }
  
  //行列の定数倍
  static double[][] Add(double[][] m1, double c)
  {
      return _calcuElementWise(m1, c, (a,b)->a+b);
  }
  static double[][] Sub(double[][] m1, double c)
  {
      return _calcuElementWise(m1, c, (a,b)->a-b);
  }
  //これはElementWiseであって行列の積ではない
  static double[][] Multiple(double c, double[][] m1)
  {
      return _calcuElementWise(m1, c, (a,b)->a*b);
  }
  static double[][] Multiple(double[][] m1, double c)
  {
      return _calcuElementWise(m1, c, (a,b)->a*b);
  }
  static double[][] Divide(double[][] m1, double c)
  {
      return _calcuElementWise(m1, c, (a,b)->a/b);
  }
  static double[][] Mod(double[][] m1, double c)
  {
      return _calcuElementWise(m1, c, (a,b)->a%b);
  }  
        
  //配列の定数倍
  public static double[] _calcuElementWise(double[] v1, double c, ScalarOperation operation)
  {
      double[] ret = new double[v1.length];

      for (int i = 0; i < v1.length; i++)
      {
          ret[i] = operation.exe(v1[i], c);
      }
      return ret;
  }
  //配列×配列
  public static double[] _calcuElementWise(double[] v1, double[] v2, ScalarOperation operation)
  {
      if (v1.length != v2.length) { return null; }

      double[] ret = new double[v1.length];

      for (int i = 0; i < v1.length; i++)
      {
          ret[i] = operation.exe(v1[i], v2[i]);
      }
      return ret;
  }
  //行列の定数倍
  static double[][] _calcuElementWise(double[][] m1, double c, ScalarOperation operation)
  {
      double[][] ret = new double[m1.length][m1[0].length];

      for (int m = 0; m < m1.length; m++)
      {
          //右に向かって走査
          for (int n = 0; n < m1[0].length; n++)
          {
              ret[m][n] = operation.exe(m1[m][n], c);
          }
      }
      return ret;
  }

  //行列×縦ベクトル
  static double[] _calcuElementWise(double[][] m, double[] v, ScalarOperation operation)
  {
      double[] ret = new double[v.length];

      for (int row_index = 0; row_index < m.length; row_index++)
      {
          //右に向かって走査
          for (int col_index = 0; col_index < m[0].length; col_index++)
          {
              ret[row_index] = operation.exe(m[row_index][col_index], v[col_index]);
          }
      }
      return ret;
  }

  //行列×行列
  static double[][] _calcuElementWise(double[][] m1, double[][] m2, ScalarOperation operation)
  {
      if (m1.length != m2.length) { return null; }
      if (m1[0].length != m2[0].length) { return null; }

      double[][] ret = new double[m1.length][m1[0].length];

      //一行ずつ取り出す[同型なのでどちらの行列を基準にしても良い]
      for (int m = 0; m < m1.length; m++)
      {
          //右に向かって走査
          for (int n = 0; n < m1[0].length; n++)
          {
              ret[m][n] = operation.exe(m1[m][n], m2[m][n]);
          }
      }
      return ret;
  }
}//MatrixMethod

interface ScalarOperation
{
  double exe(double a, double b);
}


/////////////////////////////////////////////////////////////////////////////////////////////////////////

平均、分散、共分散を用いた回帰直線

連立方程式

$$
a\sum\limits_{i=1}^{N}x_i^2+b\sum\limits_{i=1}^{N}x_i-\sum\limits_{i=1}^{N}x_iy_i=0
$$

$$
a\sum\limits_{i=1}^{N}x_i+b\sum\limits_{i=1}^{N}1-\sum\limits_{i=1}^{N}y_i=0
$$

において$${x_i}$$の平均を$${\bar x}$$と置くと

$$
\sum\limits_{i=1}^{N}x_i=N\bar x
$$

において$${y_i}$$の平均を$${\bar y}$$と置くと

$$
\sum\limits_{i=1}^{N}y_i=N\bar y
$$

$${\sum\limits_{i=1}^{N}b}$$に関してはbがただの定数なので

$$
\sum\limits_{i=1}^{N}b=Nb
$$

これを連立方程式に戻すと

$$
a\sum\limits_{i=1}^{N}x_i^2+bN\bar x-\sum\limits_{i=1}^{N}x_iy_i=0
$$

$$
aN\bar x+bN-N\bar y=0
$$

整理すると

$$
a=\frac{\sum\limits_{i=1}^N x_i y_i-N\bar x\bar y}{\sum\limits_{i=1}^N x_i^2-N\bar x^2}
$$

$$
b=\bar y - a\bar x
$$

分散

偏差の２乗の和、または２乗和と平均の２乗の差。

$$
V_{xx}=\frac{1}{n}\sum\limits_{i=1}^N(x_i-\bar x)^2=\frac{1}{n}\sum\limits_{i=1}^N x_i^2-\bar x^2
$$

yの分散も同じ。

共分散

$$
V_{xy}=\frac{1}{n}\sum\limits_{i=1}^N(x_i-\bar x)(y_i-\bar y)=\frac{1}{n}\sum\limits_{i=1}^N x_iy_i-\bar x \bar y
$$

これを用いると

$$
a=\frac{V_{xy}}{V_{xx}}
$$

$$
b=\bar y - \frac{V_{xy}}{V_{xx}}\bar x
$$

ゆえに回帰直線は分散、共分散、およびx,yの平均を用いて

$$
y=\frac{V_{xy}}{V_{xx}}(x-\bar x)+\bar y
$$

あるいは

$$
x=\frac{V_{xy}}{V_{yy}}(y-\bar y)+\bar x
$$

２次式の場合

当てはめたい式

$$
y=ax^2+bx+c
$$

正規方程式

$$
\begin{pmatrix}
\sum\limits_{i=1}^{N}x_i^4 & \sum\limits_{i=1}^{N}x_i^3 & \sum\limits_{i=1}^{N}x_i^2 \\
\sum\limits_{i=1}^{N}x_i^3 & \sum\limits_{i=1}^{N}x_i^2 & \sum\limits_{i=1}^{N}x_i\\
\sum\limits_{i=1}^{N}x_i^2 & \sum\limits_{i=1}^{N}x_i & \sum\limits_{i=1}^{N}1\\
\end{pmatrix}
\begin{pmatrix}
a \\
b \\
c \\
\end{pmatrix}
=
\begin{pmatrix}
\sum\limits_{i=1}^{N}x_i^2 y_i \\
\sum\limits_{i=1}^{N}x_iy_i \\
\sum\limits_{i=1}^{N}y_i \\
\end{pmatrix}
$$

double[] LeastSquare2(List<PVector> vertices)
{
  var n = 0;
  var xxxx_sum = 0;
  var xxx_sum = 0;
  var xx_sum = 0;
  var x_sum = 0;
  var xxy_sum = 0;
  var xy_sum = 0;
  var y_sum = 0;
  
  for(var v : vertices)
  {
    n++;
    xxxx_sum+=v.x*v.x*v.x*v.x;
    xxx_sum+=v.x*v.x*v.x;
    xx_sum+=v.x*v.x;
    x_sum+=v.x;
    xxy_sum+=v.x*v.x*v.y;
    xy_sum+=v.x*v.y;
    y_sum+=v.y;
  }
  
  double[][] A = {
    {xxxx_sum,xxx_sum,xx_sum},
    {xxx_sum,xx_sum,x_sum},
    {xx_sum,x_sum,n}
    };
  double[] b = {xxy_sum,xy_sum,y_sum};
  var x = MatrixMethod.CramersRules(A,b);
  
  return x;
}

使い方

  var x = LeastSquare2(input);
  if(x==null||x.length<3){return;}
  float a = (float)(x[0]);
  float b = (float)(x[1]);
  float c = (float)(x[2]);
  
  List<PVector> vertices = new ArrayList<PVector>();
  int resolution = 100;
  float start_x = -width/2;//計算用x
  for(int i = 0; i<resolution; i++)
  {
    var unitx = width/resolution;    
    var dx = start_x+unitx*i;//計算用入力x
    var dy = a*dx*dx+b*dx+c;//計算用出力y
    vertices.add(new PVector(dx+origin.x,dy+origin.y));
  }
  
  for(int i = 0; i<vertices.size()-1; i++)
  {
    var sv = vertices.get(i);
    var ev = vertices.get(i+1);
    line(sv.x,sv.y,ev.x,ev.y);
  }

inputリストは表示用の円の座標から原点を引いて、計算用に直したもの。また、この例では原点は画面中央であることを前提としてある。

float start_x = -width/2

部分に注意。

  List<PVector> input = new ArrayList<PVector>();
  for(var v : this.Vertices)
  {
    input.add(v.copy().sub(origin));
  }

Ｎ次式の場合

当てはめたい式

$$
y=c_0x^n+c_1x^{n-1}+…c_{n-1}x+c_n=(x^n,x^{n-1}…x,1)
\begin{pmatrix}
c_0 \\
c_1 \\
\vdots \\
c_n \\
\end{pmatrix}
=\bm x \cdot \bm c
$$

正規方程式

$$
\begin{pmatrix}
\sum\limits_{i=1}^{N}x_i^{2n} & \sum\limits_{i=1}^{N}x_i^{2n-1} &\cdots & \sum\limits_{i=1}^{N}x_i^{n} \\
\sum\limits_{i=1}^{N}x_i^{2n-1} & \sum\limits_{i=1}^{N}x_i^{2n-2} &\cdots & \sum\limits_{i=1}^{N}x_i^{n-1} \\
\vdots & \vdots & \ddots & \vdots \\
\sum\limits_{i=1}^{N}x_i^{n} & \sum\limits_{i=1}^{N}x_i^{n-1} &\cdots & \sum\limits_{i=1}^{N}1\\
\end{pmatrix}
\begin{pmatrix}
c_0 \\
c_1 \\
\vdots \\
c_n \\
\end{pmatrix}
=
\begin{pmatrix}
\sum\limits_{i=1}^{N}x_i^n y_i \\
\sum\limits_{i=1}^{N}x_i^{n-1} y_i \\
\vdots \\
\sum\limits_{i=1}^{N}y_i \\
\end{pmatrix}
$$

総和記号がいかついが、これはデータ点を全部放り込んで足すくらいしか言ってない。

$$
\begin{pmatrix}
x^{2n}    & x^{2n-1} & \cdots  & x^n \\
x^{2n-1} & x^{2n-2} & \cdots  & x^{n-1} \\
\vdots     & \vdots    & \ddots & \vdots \\
x^{n}       & x^{n-1}  & \cdots  & 1 \\
\end{pmatrix}
$$

係数と関数の線形和

$${x^n}$$をただの1変数関数f(x)とみて

$$
y=c_1f_1(x)+c_2f_2(x)+…c_nf_n(x)=(f_1,f_2,…f_n)
\begin{pmatrix}
c_1 \\
c_2 \\
\vdots \\
c_n \\
\end{pmatrix}
=\bm f \cdot \bm c
$$

$$
\begin{pmatrix}
\sum\limits_{i=1}^{N} f_1(x_i)f_1(x_i) & \sum\limits_{i=1}^{N}f_1(x_i)f_2(x_i) &\cdots & \sum\limits_{i=1}^{N}f_1(x_i)f_n(x_i) \\
\sum\limits_{i=1}^{N} f_2(x_i)f_1(x_i) & \sum\limits_{i=1}^{N}f_2(x_i)f_2(x_i) &\cdots & \sum\limits_{i=1}^{N}f_2(x_i)f_n(x_i) \\
\sum\limits_{i=1}^{N} f_3(x_i)f_1(x_i) & \sum\limits_{i=1}^{N}f_3(x_i)f_2(x_i) &\cdots & \sum\limits_{i=1}^{N}f_3(x_i)f_n(x_i) \\
\sum\limits_{i=1}^{N} f_n(x_i)f_1(x_i) & \sum\limits_{i=1}^{N}f_n(x_i)f_2(x_i) &\cdots & \sum\limits_{i=1}^{N}f_n(x_i)f_n(x_i) \\
\end{pmatrix}
\begin{pmatrix}
c_1 \\
c_2 \\
\vdots \\
c_n \\
\end{pmatrix}
=
\begin{pmatrix}
\sum\limits_{i=1}^{N}f_1(x_1) y_i \\
\sum\limits_{i=1}^{N}f_2(x_1) y_i \\
\vdots \\
\sum\limits_{i=1}^{N}f_n(x_1) y_i \\
\end{pmatrix}
$$

$$
\begin{pmatrix}
f_1f_1    & f_1f_2 & \cdots  & f_1f_n \\
f_2f_1    & f_2f_2 & \cdots  & f_2f_n \\
\vdots     & \vdots    & \ddots & \vdots \\
f_nf_1    & f_nf_2 & \cdots  & f_nf_n \\
\end{pmatrix}
$$

この時、

$$
\sum\limits_{i=1}^N f_j(x_i) f_k(x_i)=0 \quad (j \neq k)
$$

となるような関数らを選んでおけば、係数cは正規方程式を解くことなくただの割り算で求まる。総和記号を積分に拡張することを考えると、観測されたデータ点$${x_i}$$のインデックスは消えてxとなり、$${y_i}$$はf(x)となる。それに伴い近似関数を構成するいくらかの関数群を$${\phi}$$で表すこととすると、この関数群は

$$
\int_a^b \phi_j(x) \phi_k(x)dx=0 \quad (j \neq k)
$$

なる性質を満たすように選ばれると大変に都合が良いことが分かる。この好ましい性質を関数の直交性と呼び、上記の計算を関数同士の内積と定義する。すると関数というものがベクトルと似たような感じに扱えることが分かる。

ベクトルの内積は成分同士の積の総和であったが、ベクトルのインデックスが連続しておって、成分もまた連続しておるものが関数であると考えると、成分同士の積の総和はまさしく上記の積分の式である。

ベクトルもまた、内積してゼロになるようなベクトルを直交しているとみなし、直交しているようなベクトルを基底とみなしてあれやこれやと空間を構築するのであった。関数もまた同じようなことができる。

$$
\begin{pmatrix}
\int_a^b \phi_1(x)\phi_1(x)dx & & & \\
& \int_a^b \phi_2(x)\phi_2(x) & &  \\
& &\ddots & \\
& & & \int_a^b \phi_n(x)\phi_n(x) \\
\end{pmatrix}
\begin{pmatrix}
c_1 \\
c_2 \\
\vdots \\
c_n \\
\end{pmatrix}
=
\begin{pmatrix}
\phi_1(x) f(x) \\
\phi_2(x) f(x) \\
\vdots \\
\phi_n(x) f(x) \\
\end{pmatrix}
$$