有限差分法1D
差分法は微分方程式を近似的に解く方法の一つ。
微分方程式を近似的に解く他の方法には有限要素法などがある。
差分法は微分方程式に存在する微分項を、対応する近似式に単純に置き換えるものである。
微分項には
1変数1階微分、1変数2階微分……
2変数1階微分、2変数2階微分……
3変数1階微分、3変数2階微分……
なんかがあり、
各々の微分項に対し、近似式の取り方は一通りではない。
例えば以下は1変数1階微分。これはいわゆる微分の公式から極限をとっぱらったものである。

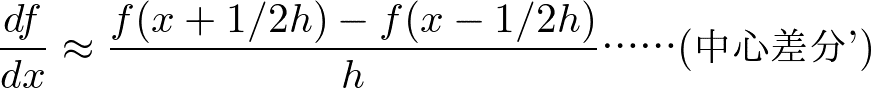
1変数2階微分の近似式は、1変数1階微分の近似式を組み合わせれば作ることができる。また、テイラー展開からも導くことができる。
以下、1変数1階微分の近似式df/dx=f'(x)に対してx及びx+hを入力し、下記の式にブチ込んで計算する。

しかし結局の所、一番使われる1変数2階微分の近似式は以下の形式である。

2変数の1階微分は偏微分となる。すなわち関数に入力が (x, y) とあって、関数の出力が入力xに対してどれだけ反応するのか、入力yに対してどれだけ反応するのか、その割合の近似であるからして、近似式は各々の変数に対応して増える。

2変数の2階微分はこれまでのことをごちゃごちゃとこねくり回すか、あるいは教科書に書かれていることを疑うこともなくうやうやしく受け入れて

ここまで登場した部品を用いれば、簡単な微分方程式なら数値的に解くことができて、例えば死ぬほど簡単にした拡散方程式

この関数を数値的に求めるためには、u(x,t)のtに関する1階偏微分とxに関する2階偏微分に近似差分式をブチ込む。

この時u(x,t+Δt)に対して漸化式を立てると陽的解法となる。
微分方程式は時間と空間の座標を入力とするなんかの量である。なんかの量とは、例えば熱とか密度とか画像の輝度であるとか、何でも良い。その量を記述する微分方程式に時間に関する微分項が含まれているのなら、その量は時間的に変化しているといえる。アニメーションしているといえる。逆に時間に関する微分項が存在しないのであれば、そのなんかの量は時間的に変化していない。静止画的な、写真的なものである。あるといえる。
ある量を記述する微分方程式に空間に関する微分項が含まれているのなら、その量は他の空間の量に影響を受けて決定される。ある空間の量を決定するために他の空間の量が必要となり、それを求めるためにまた別の空間の量が必要となる。これを繰り返すときりがないので、どっかの量は最初の段階であらかじめこちら側で決めておかなければならない。これが初期値(時間用)、境界値(空間用)である。
これを踏まえて死ぬ程簡単な拡散方程式を見てみると、この式は最初にある時間の空間を用意すれば、次の時間の空間の量は全て計算できることを意味している。

からの式変形。ただしr=Δt/Δx。

最終的に即座にプログラムに導入可能な拡散方程式の陽解法、以下を得る。

初期条件をすべての要素が0の配列とし、境界条件を配列の端っこで0とすると
Pythonの場合
#データ
p = np.zeros(w, np.float32)
f = np.zeros(w, np.float32)
n = np.zeros(w, np.float32)
#拡散方程式
dr = 0.2;#0.0-0.5
def difference(ndarray, r):
next = np.ndarray(ndarray.shape)
for index, value in np.ndenumerate(ndarray):
x = index[0]
if(x == 0):
next[x]=0
continue
if(x == ndarray.shape[0]-1):
next[x]=0
continue
next[x] = dr*f[x-1] + (1-2*dr)*f[x] + dr*f[x+1];
return next全部
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
w = 200
h = 255
x_tick = np.arange(0, 200, 1)
#データ
p = np.zeros(w, np.float32)
f = np.zeros(w, np.float32)
n = np.zeros(w, np.float32)
#拡散方程式
dr = 0.2;#0.0-0.5
#移流方程式
ar = 0.5;#0.0-1.0
#波動方程式
wr = 0.5;#0.0-1.0
def difference(ndarray, r):
next = np.ndarray(ndarray.shape)
for index, value in np.ndenumerate(ndarray):
x = index[0]
if(x == 0):
next[x]=0
continue
if(x == ndarray.shape[0]-1):
next[x]=0
continue
next[x] = dr*f[x-1] + (1-2*dr)*f[x] + dr*f[x+1];
#next[x] = (1-ar)*f[x] + ar*f[x-1];
#next[x] = wr*wr*f[x-1] + (2-2*wr*wr)*f[x] + wr*wr*f[x+1] - p[x];
return next
def onclick(event):
global p,f,n
mx = event.xdata
my = event.ydata
f[int(mx)]=my
fig, ax = plt.subplots()
line2d, = ax.plot([], [])
connection_id = fig.canvas.mpl_connect('button_press_event', onclick)
ax.set_xlim(0, 200)
ax.set_ylim(0, 255)
def update(frame):
global x_tick, p, f, n, ax, line2d
n = difference(f, 0.25)
line2d.set_data(x_tick, n)#常にクリアしていることに相当すると思われる
p = np.copy(f)
f = np.copy(n)
#interval=ミリ秒
ani = animation.FuncAnimation(fig, update, interval=1)
plt.show()processingだと
int window_width = 500;
int window_height = 500;
void settings()
{
size(window_width, window_height);
}
float[] p;//fx_prev
float[] f;
float[] n;//fx_next
void setup()
{
p = new float[window_width];
f = new float[window_width];
n = new float[window_width];
}
int mx;
int my;
//拡散方程式
float dr = 0.2;//0.0-0.5
//移流方程式
float ar = 0.8;//0.0-1.0
//波動方程式
float wr = 0.5;//0.0-1.0
void draw()
{
background(255);
if(mousePressed==true)
{
mx=mouseX;
my=window_height-mouseY;//y+を下とする
f[mx]=my;
}
for(int x = 1; x < f.length-1; x++)
{
//拡散方程式:current,next
n[x] = dr*f[x-1] + (1-2*dr)*f[x] + dr*f[x+1];
//移流方程式:current,next
//n[x] = (1-ar)*f[x] + ar*f[x-1];
//波動方程式:prev,current,next
//n[x] = wr*wr*f[x-1] + (2-2*wr*wr)*f[x] + wr*wr*f[x+1] - p[x];
}
//draw
for(int x = 0; x < f.length; x++)
{
line(x,window_height-0,x,window_height-f[x]);
}
System.arraycopy(f,0,p,0,f.length);
System.arraycopy(n,0,f,0,n.length);参考文献
桑原邦郎 ・河村哲也 編著 流体計算と差分法 朝倉書店
平野博之 流れの数値計算と可視化 丸善出版
J.H.ファーツィガー(著)、M.ペリッチ(著)、小林敏雄(訳)、大島伸行(訳)、坪倉誠(訳)
コンピュータによる流体力学 丸善出版
H.K.Versteeg(著)、W.Malalasekera(著)、松下洋介(訳)、齋藤泰洋(訳)、青木秀之(訳)、三浦隆利(訳)
数値流体力学 森北出版
