有限差分法2D

二次元空間の単純化した拡散方程式

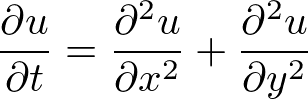
近似式をブチ込む。

ここでΔx=Δyとする

r=Δt/Δxとすると

Python

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import scipy.sparse as sp

x_max = 100
y_max = 100
z_max = 255

xs = np.arange(0, x_max, 1)
ys = np.arange(0, y_max, 1)
xs, ys = np.meshgrid(xs, ys)

z_level = np.arange(0, z_max, 50)

pp = np.zeros((y_max,x_max), np.float32)
ff = np.zeros((y_max,x_max), np.float32)
nn = np.zeros((y_max,x_max), np.float32)

#拡散方程式
dr = 0.1;#0.0-0.5
#移流方程式
ar = 0.5;#0.0-1.0
#波動方程式
wr = 0.5;#0.0-1.0

def difference(p, f, n, r):    
   next = np.ndarray(f.shape)

   for index, channel in np.ndenumerate(f):      
       row = index[0]
       col = index[1]
       x = col
       y = row

       if(x==0 or y==0):
           next[x,y]=0
           continue
       if(y == f.shape[0]-1 or x == f.shape[1]-1):
           next[x,y]=0
           continue

       next[x,y] = r*(f[x-1,y]+f[x+1,y]+f[x,y-1]+f[x,y+1])-(1-4*r)*f[x,y]
       #next[x,y]=(2-4*wr*wr)*f[x,y]+wr*wr*(f[x-1,y]+f[x+1,y]+f[x,y-1]+f[x,y+1])-p[x,y]

   return next

def onclick(event):
   global pp,ff,nn

   mx = event.xdata
   my = event.ydata

   ff[int(my),int(mx)]=255
   
fig, ax = plt.subplots()
cid = fig.canvas.mpl_connect('button_press_event', onclick)

import time

def update(frame):
   global pp,ff,nn, ax, xs, ys, im

   #clear
   plt.cla()  

   ax.set_xlim(0, x_max)
   ax.set_ylim(0, y_max)
   
   nn = difference(pp, ff, nn, 0.25)

   cnt= plt.contourf(xs, ys, ff, 10)

   pp = np.copy(ff)
   ff = np.copy(nn)    
   
   return cnt

#interval=ミリ秒
ani = animation.FuncAnimation(fig, update, interval=100)
plt.show()

processing

int window_width = 500;
int window_height = 500;

int w;
int h;

void settings()
{
 size(window_width, window_height);
}

float[][] p;//fxy_prev
float[][] f;
float[][] n;//fxy_next

void setup()
{
 p = new float[window_width][window_height];//=fx_0
 f = new float[window_width][window_height];//=fx_0  
 n = new float[window_width][window_height];
   
 w = window_width;
 h = window_height;
}

void copy(float[][]source, float[][]target)
{
 for(int i = 0; i<source.length; i++)
 {
   for(int j = 0; j<source.length; j++)
   {
     target[i][j]=source[i][j];
   }
 }  
}

int mx;
int my;

//拡散方程式
float dr = 0.25;//0.0-0.25
//移流方程式
float ar = 0.1;//0.0-1.0//0.295//多分0.25が限界
//波動方程式
float wr = 0.5;//0.0-1.0

void update()
{
 for(int y = 1; y < h-1; y++)
 {
   for(int x = 1; x < w-1; x++)
   {
     //２変数拡散４近傍
     n[x][y]=(1-4*dr)*f[x][y]+dr*(f[x-1][y]+f[x+1][y]+f[x][y-1]+f[x][y+1]);
     //２変数拡散８近傍
     //n[x][y]=(1-8*dr)*f[x][y]+dr*(f[x-1][y]+f[x+1][y]+f[x][y-1]+f[x][y+1]+f[x-1][y-1]+f[x+1][y-1]+f[x-1][y+1]+f[x+1][y+1]);
           
     //２変数移流:左上から右下へ
     //n[x][y]=(1-2*ar)*f[x][y]+ar*f[x-1][y]+dr*f[x][y-1];     
     //２変数移流:左から右へ
     //n[x][y]=(1-2*ar)*f[x][y]+ar*f[x-1][y]+dr*f[x][y];     
     
     //２変数波動方程式
     //n[x][y]=(2-4*wr*wr)*f[x][y]+wr*wr*(f[x-1][y]+f[x+1][y]+f[x][y-1]+f[x][y+1])-p[x][y];            
   }    
 }
}

void draw()
{
 background(255);

 //input
 if(mousePressed==true)
 {
   mx=mouseX;
   my=mouseY;//y+を下とする
   
   f[mx][my]+=300;
 }
 
 //update
 update();

 //正規化前にコピー
 copy(f,p);
 copy(n,f);  
 
 //draw
 loadPixels();
 for(int y = 0; y < h; y++)
 {
   for(int x = 0; x < h; x++)
   {      
     //正規化
     float val = n[x][y];     
     if(val>255){val=255;}
           
     pixels[y*w+x]=color(255-val,255-val,255-val);
   }
 }
 updatePixels();
 
 //draw:重すぎ
 //for(int x = 0; x < w; x++)
 //{
 //  for(int y = 0; y < h; y++)
 //  {
 //    if(n[x][y]!=0)
 //    {
 //      int a = 0;
 //    }
     
 //    //int col = (int)n[x][y];
 //    int col = 255-(int)n[x][y];
 //    //int col = 255-(int)map(n[x][y],0,n[x][y],0,255);
 //    stroke(col,col,col);
 //    point(x,y);
 //  }
 //}
}

​