ラプラス・ポアソン方程式の近似解法（差分法、直接法）

※注意　この記事はまだちょっとバグっております。

そもそもラプラス方程式とかポアソン方程式とかは何か

境界、フチっこの値が与えられた時の内部の量、状態を表す方程式。
時間に関する項が無いため、ある瞬間の、あるいは変化の終わった、時間に応じて変化しない状態を記述する。
例えばある人の顔面につきたてのお餅を叩き付けた場合、そのお餅の形状はラプラス方程式で記述されるであろう。

ラプラス方程式２Ｄ

ポアソン方程式２Ｄ

２階の偏微分を近似する差分近似式は

ラプラス方程式を差分近似式で近似すると

ここで(j-1,k)は(x-1,y)、(j+1,k)は(x+1,y)、(j,k-1)は(x,y-1)、(j,k+1)は(x,y+1)を示す。このあたりはプログラムに直す時や、ディスプレイに表示する時に適時読み替えなければならない。

Δx=Δyとするとラプラス方程式の差分近似は

同様にしてポアソン方程式の差分近似は

これらは結局、あるセルの値を決定するために、あるセルの上下左右のセルの値を必要とすることを意味する。

この近似式は領域の全てのセルに付いて並び立つ。
この近似式は境界の値が全て既知として、あらかじめ定まっていなければ解くことはできない。また、領域のセルが２つ以上存在するなら、近似式は単独では解くことができず、全ての式を同時に解く必要がある。すなわち連立方程式を立てる必要がある。

連立方程式を行列の演算としてまとめると以下の矢印左のようになり、これを解くには矢印右のように逆行列を求めてうんぬんと説明される。xは基本的には全ての未知数、全ての未知のセルをならべたベクトル、１次の配列である。bベクトルはラプラス方程式なら全て０のベクトル。ポアソン方程式なら全て定数のベクトルである。

プログラムでこれを計算する場合、最も基本となるのはガウスの消去法である。ガウスの消去法はxベクトルを直接求めに行く。逆行列はその副産物として途中で生成できる。すなわち数式にのっとって逆行列を求めてからその積をとるのは少し無駄である（しかしそもそも、消去法を始めとする、いわゆる直接法は、計算の速度がそれほど速くない。ある程度の規模以上の行列計算は反復法が用いられるであろう）。

直接法を用いる場合、A行列やbベクトルの構築が重要な操作となる。この場合おそらく２通りの構築方法が考えられるであろう。１つはxベクトルが完全に未知の成分、未知のセルのみで構成される方法。もう１つはxベクトルに既知の境界成分、セルを混ぜ込んでしまう方法である。

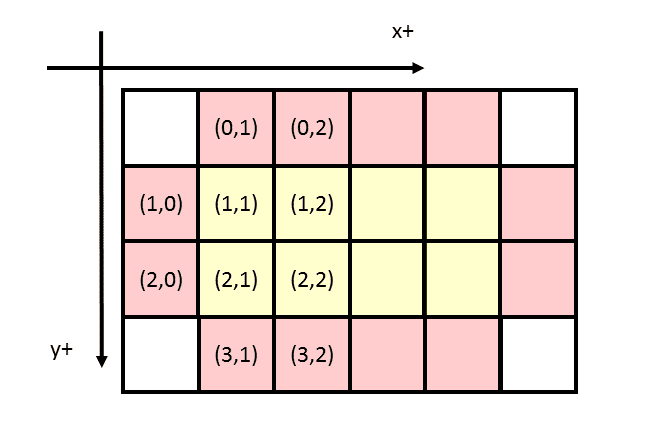
例えば以下の図の場合、xベクトルを未知のみとするならそのベクトルの成分数は4であり、A行列は4×4となる。
xベクトルに既知の境界成分もほりこむ場合、xベクトルの成分数は16となりA行列は16×16となる。

上図に関して4×4のA行列は下図。xベクトルは全て未知。bベクトルはラプラス方程式ならはじめ全てゼロとなり、既知の境界値はこの項に移項される。

16×16のA行列は下図。xベクトルは既知と未知とが混在。xベクトルに既知の成分が混ざっていても、A行列の対応する対角成分を1とすれば計算に支障はでない。

これらの行列は行ごとに見る。行は1つ1つが連立方程式の1つの式である。
すなわち、あるセルの未知の値を求めるために、その計算に関わっている他の未知のセルに係数を付けて式に残す。計算に無関係な未知のセルは０を掛けて消す。既知のセルは、それが計算に関わるなら前述の通りbベクトルに移項する。無関係ならばやはり0を掛けて消す。

両者の違いは、インデックス操作のわずらわしさである。例えば以下の図で、(1,2)と(2,2)はxベクトル内でどれだけ離れているか、を計算するのは前者には面倒くさい。後者ならA行列の列数を足したり引いたりすれば、1次元ベクトル内で上下に移動できる。

領域が単純な矩形なら、前者におけるA行列、およびbベクトルは以下のように構築することができるであろう。

ここで下図において
region_matrixは4×6
xベクトルは要素8
bベクトルは要素8
A行列は8×8
laplace_mapはxベクトルとかbベクトルのインデックスを入力するとregion_matrixの座標を返すというだけのやつ
boundary_indexはregion_matrix内で指定した境界のインデックス（ただし1次元、下図においては0-23の範囲）を格納したもの。

 void Assembly()
 {    
   int r_row_count = this.region_matrix.length;    
   int r_col_count = this.region_matrix[0].length;  
   
   //region_matrix内でのオフセット
   int r_x_offset = 1;
   int r_y_offset = r_col_count;
   
   //A内でのオフセット
   int a_x_offset = 1;
   int a_y_offset = r_col_count-2;//境界が左右に合計２列という前提
       
   this.reset_laplace_b();
   
   //有効領域のみ走査
   for(int i = 0; i<laplace_b.length; i++)
   {
     A[i][i]-=4;
     
     MatrixIndex id = laplace_map[i];
     int x_vector_index = id.y*r_col_count+id.x;
     int up = x_vector_index-r_y_offset;
     int down = x_vector_index+r_y_offset;
     int left = x_vector_index-r_x_offset;
     int right = x_vector_index+r_x_offset;
     
     //上
     if(boundary_index.contains(up))
     {
       this.laplace_b[i]-=region_matrix[id.y-1][id.x];
     }
     else
     {
       A[i][i-a_y_offset]+=1;//行内の操作しかしない
     }
     
     //下
     if(boundary_index.contains(down))//領域外（有効Ａからはみ出る＝境界）
     {
       this.laplace_b[i]-=region_matrix[id.y+1][id.x];
     }
     else
     {
       A[i][i+a_y_offset]+=1;//行内の操作しかしない
     }
     
     //左
     if(boundary_index.contains(left))//領域外（有効Ａからはみ出る＝境界）
     {        
       this.laplace_b[i]-=region_matrix[id.y][id.x-1];
     }
     else
     {
       A[i][i-a_x_offset]+=1;
     }          
     
     //右
     if(boundary_index.contains(right))//領域外（有効Ａからはみ出る＝境界）
     {
       this.laplace_b[i]-=region_matrix[id.y][id.x+1];
     }
     else
     {  
       A[i][i+a_x_offset]+=1;        
     }      
   }
 }

後者の場合、余計なインデックス操作は減る。

 void Assembly()
 {
   int r_row_count = this.region_matrix.length;
   int r_col_count = this.region_matrix[0].length;
   
   this.reset_laplace_b();
   
   //xベクトル用
   int x_offset = 1;
   int y_offset = r_col_count;
   
   //xベクトルでA行列の対角を走る
   for(int i = 0; i<this.x.length; i++)
   {
     int up;
     int down;
     int left;
     int right;
     
     //xベクトル基準
     up=i-y_offset;      
     if(up<0){up=-1;}
     down=i+y_offset;
     if(x.length-1<down){down=-1;}
     left=i-x_offset;
     if(left<0){left=-1;}
     right=i+x_offset;
     if(x.length-1<right){right=-1;}
     
     if(this.boundary_index.contains(i))
     {
       this.laplace_b[i]+=this.x[i];
       this.A[i][i]=1;
       continue;
     }
     else
     {
       this.A[i][i]-=4;
     }
     
     if(0<=up)
     {       
         //up
         if(this.boundary_index.contains(up))
         {
           //ある行の方程式を成立させるために
           //bベクトルの対象行からxベクトル成分を引く
           //bベクトルは最大で４回分引かれるであろう
           this.laplace_b[i]-=this.x[up];
         }
         else
         {
           this.A[i][up]+=1;
         }       
     }
     
     if(0<=down)
     {
         //down
         if(this.boundary_index.contains(down))
         {
           this.laplace_b[i]-=this.x[down];
         } 
         else
         {
           this.A[i][down]+=1;
         }
     }
     
     if(0<=left)
     {      
         //left
         if(this.boundary_index.contains(left))
         {
           this.laplace_b[i]-=this.x[left];
         }
         else
         {
           this.A[i][left]+=1;
         }
     }
     
     if(0<=right)
     {
         //right
         if(this.boundary_index.contains(right))
         {
           this.laplace_b[i]-=this.x[right];
         }
         else
         {
           this.A[i][right]+=1;
         }      
     }      
   }
 }

前者のヤツだいたい(4×4)

import org.apache.commons.math3.linear.*; 
import org.apache.commons.math3.exception.*;//例外

int window_width = 1200;
int window_height = 800;

int w;
int h;

void settings()
{
 size(window_width, window_height);
}

void setup()
{    
 w = window_width;
 h = window_height;
 
 fdm2d = new FDM2D(4,4);
}

FDM2D fdm2d;

void draw()
{
 background(255);
 fdm2d.draw_matrix_value(fdm2d.A);
}

double[] solve(double[][]A, double[]b)
{
 double[]x = new double[b.length];
 
 RealMatrix solver_U = exe_solver(A, b);
 if(solver_U == null)    {      return null;    }
 
 for(int i = 0; i<x.length; i++)
 {
   float u = (float)solver_U.getEntry(i, 0); 
   x[i] = u;
 }
 return x;    
}

boolean is_singlar = false;  
RealMatrix exe_solver(double[][]A, double[]b)
{        
 RealMatrix solver_A = new Array2DRowRealMatrix(A);
 RealMatrix solver_b = new Array2DRowRealMatrix(b);      
   
 try
 {
   //特異行列は例外で処理
   RealMatrix solver_AI = MatrixUtils.blockInverse(solver_A, 0); //逆行列    
   RealMatrix solver_u = solver_AI.multiply(solver_b);
   is_singlar = false;
   
   return solver_u;      
 }
 catch(SingularMatrixException sme)
 {
   is_singlar = true;
 }
 catch(NullPointerException npe)
 {
   is_singlar = true;
 }    
 catch(MathArithmeticException mae)
 {
   is_singlar = true;      
   //ノルムゼロ
 }
 catch(MaxCountExceededException mcee)
 {
   is_singlar = true;      
   //収束失敗      
 }
 return null;
}  

//sourceからtargetに要素をコピー
void copy_matrix(double[][] source, double[][] target)
{
 int m = source.length;
 int n = source[0].length;
 
 for(int i = 0; i<m; i++)
 {
   for(int j = 0; j<n; j++)
   {
     target[i][j]=source[i][j];
   }
 }  
}

class MatrixIndex
{
 int x;
 int y;
 
 MatrixIndex(int x_, int y_)
 {
   this.x=x_;
   this.y=y_;
 }
}

class FDM2D
{
 //計算対象の領域
 double[][] region_matrix;
 //境界となるセルのリスト(1次元配列のインデックスとして記録)
 ArrayList<Integer> boundary_index = new ArrayList<Integer>();
 
 //有効領域のみの行列
 double[][] A;
 //solve後にしか確定しない
 double[] x;
 
 double[] laplace_b;//=>make_laplace_b()
 MatrixIndex[] laplace_map;
 
 double[] poisson_b;//=>make_poisson_b(double value)
 
 //region行列から境界を除いた要素数、これがx,bベクトルの次元となる
 int calcu_n()
 {
   int row_count = this.region_matrix.length;
   int col_count = this.region_matrix[0].length;
   
   int ret = (row_count*col_count)-boundary_index.size();
   return ret;
 }
 
 void make_laplace_map()
 {
   laplace_map = new MatrixIndex[this.laplace_b.length];
   
   int count = 0;
   for(int i = 0; i<region_matrix.length; i++)
   {
     for(int j = 0; j<region_matrix[0].length; j++)
     {
       if(boundary_index.contains(i*region_matrix[0].length+j))
       {
         continue;
       }
       else
       {
         laplace_map[count] = new MatrixIndex(j,i);
         count++;
       }        
     }
   }
 }

 void reset_laplace_b()
 {
   for(int i = 0; i<this.laplace_b.length; i++)
   {
     this.laplace_b[i]=0;
   }
 }
 
 double[] make_laplace_b()
 {    
   double[] ret = new double[calcu_n()];
   return ret;
 }
 
 void reset_poisson_b(double value)
 {
   for(int i = 0; i<this.poisson_b.length; i++)
   {
     this.poisson_b[i]=value;
   }
 }
 
 double[] make_poisson_b(double value)
 {
   double[] ret = new double[calcu_n()];
   for(int i = 0; i<ret.length; i++)
   {
     ret[i]=value;
   }
   
   return ret;
 }
 
 //matrix座標を入力し、その座標を境界に指定する
 void set_boundary(int x, int y)
 {
   int col_count = this.region_matrix[0].length;
   int index = col_count*y+x;    
   if(!this.boundary_index.contains(index))
   {
     this.boundary_index.add(index);
   }    
 }
 
 //matrixの外周を境界に指定(インデックスで指定)
 void set_arround_boundary()
 {
   int row_count = this.region_matrix.length;    
   int col_count = this.region_matrix[0].length;
   
   //上端
   set_row_to_boundary(0);
   //下端
   set_row_to_boundary(row_count-1);
   //左端
   set_col_to_boundary(0);
   //右端
   set_col_to_boundary(col_count-1);
 }  
 
 //領域の行単位で境界に設定する
 void set_row_to_boundary(int row_index)
 {
   int col_count = this.region_matrix[0].length;           
   for(int col_index = 0; col_index<col_count; col_index++)
   {
     set_boundary(row_index, col_index);
   }
 }
 
 //領域の列単位で境界に設定する
 void set_col_to_boundary(int col_index)
 {
   int row_count = this.region_matrix.length;  
   for(int row_index = 0; row_index<row_count; row_index++)
   {
     set_boundary(row_index, col_index);
   }
 }
 
 //A,bを組み立てる
 void Assembly()
 {    
   int r_row_count = this.region_matrix.length;    
   int r_col_count = this.region_matrix[0].length;  
   
   //region_matrix内でのオフセット
   int r_x_offset = 1;
   int r_y_offset = r_col_count;
   
   //A内でのオフセット
   int a_x_offset = 1;
   int a_y_offset = r_col_count-2;//境界が左右に合計２列という前提
       
   this.reset_laplace_b();

   //有効領域のみ走査
   for(int i = 0; i<laplace_b.length; i++)
   {
     A[i][i]-=4;
     
     MatrixIndex id = laplace_map[i];
     int x_vector_index = id.y*r_col_count+id.x;
     int up = x_vector_index-r_y_offset;
     int down = x_vector_index+r_y_offset;
     int left = x_vector_index-r_x_offset;
     int right = x_vector_index+r_x_offset;
     
     //上
     if(boundary_index.contains(up))
     {
       this.laplace_b[i]-=region_matrix[id.y-1][id.x];
     }
     else
     {
       //A[i-1][i]+=1;
       A[i][i-a_y_offset]+=1;//行内の操作しかしない
     }
     
     //下
     if(boundary_index.contains(down))//領域外（有効Ａからはみ出る＝境界）
     {
       this.laplace_b[i]-=region_matrix[id.y+1][id.x];
     }
     else
     {
       //A[i+1][i]+=1;  
       A[i][i+a_y_offset]+=1;//行内の操作しかしない
     }
     
     //左
     if(boundary_index.contains(left))//領域外（有効Ａからはみ出る＝境界）
     {        
       this.laplace_b[i]-=region_matrix[id.y][id.x-1];
     }
     else
     {
       //A[i][i-1]+=1;
       A[i][i-a_x_offset]+=1;
     }          
     
     //右
     if(boundary_index.contains(right))//領域外（有効Ａからはみ出る＝境界）
     {
       this.laplace_b[i]-=region_matrix[id.y][id.x+1];
     }
     else
     {
       //A[i][i+1]+=1;     
       A[i][i+a_x_offset]+=1;        
     }      
   }
 }
 
 //this.region_matrixに境界値を設定
 void set_row_value(int row, double value)
 {
   for(int i = 0; i<this.region_matrix[0].length; i++)
   {
     this.region_matrix[row][i]=value;
   }    
 }
 
 //this.region_matrixに境界値を設定
 void set_col_value(int col, double value)
 {
   for(int i = 0; i<this.region_matrix.length; i++)
   {
     this.region_matrix[i][col]=value;
   }        
 }
 
 //コンストラクタ
 FDM2D(int row_count, int col_count)
 {
   region_matrix = new double[row_count][col_count];
      
   set_row_value(0,0);
   set_row_value(row_count-1, 0);
   set_col_value(0,0);
   set_col_value(col_count-1, 10);    
   //boundary_indexの作成
   this.set_arround_boundary();
   
   this._init();
 }
 
 void _init()
 {
   //直説法    
   //bベクトル
   this.laplace_b = make_laplace_b();
   //this.poisson_b = make_poisson_b();
   //bベクトルのregion_matrixの位置
   this.make_laplace_map();
   this.x = new double[this.laplace_b.length];
   int n = calcu_n();
   this.A = new double[n][n];    
   this.Assembly();    
   this.fdm_solve();
   this.x_to_region();
 }
 
 void draw()
 {
   int row_count = this.region_matrix.length;
   int col_count = this.region_matrix[0].length; 
   
   float max = (float)max(this.region_matrix);
   
   //draw
   loadPixels();
   for(int y = 0; y < row_count; y++)
   {
     for(int x = 0; x < col_count; x++)
     {      
       //正規化
       float val = (float)this.region_matrix[y][x];  
       val = 255*(val/max);
       if(val>255){val=255;}
             
       pixels[y*w+x]=color(255-val,255-val,255-val);
     }
   }
   updatePixels();
 }
 
 int xt_offset = 20;
 int yt_offset = 20;
 
 void draw_matrix_value(double[][] mat)
 {    
   int row_count = mat.length;
   int col_count = mat[0].length; 
   
   textSize(16);
   fill(0);
   
   for(int y = 0; y < row_count; y++)
   {
     for(int x = 0; x < col_count; x++)
     {      
       double dval = mat[y][x];
       int val = (int)dval;
       String st = str(val);
       text(st,x*xt_offset,y*yt_offset, xt_offset, yt_offset);
     }
   }    
 }
 
 //Ax=b
 void fdm_solve()
 {
     double[] solved_x = solve(this.A, this.laplace_b);
     System.arraycopy(solved_x, 0, this.x, 0, solved_x.length);      
 }
 
 //xベクトルからregion_matrixへ変換
 void x_to_region()
 {
   for(int i = 0; i<this.x.length; i++)
   {
     MatrixIndex id = laplace_map[i];
     this.region_matrix[id.y][id.x] = x[i];
   }   
 }
}

後者のヤツだいたい(16×16)

class FDM2D
{
 
 //計算対象の領域
 double[][] region_matrix;
 //境界となるセルのリスト(1次元配列のインデックスとして記録)
 ArrayList<Integer> boundary_index = new ArrayList<Integer>();
 
 double[] x;//=>make_region_array()
 
 double[] laplace_b;//=>make_laplace_b()
 
 double[] poisson_b;//=>make_poisson_b(double value)
 
 //領域が4×4ならA行列は16×16
 double A[][];
 
 double[] make_region_array()
 {
   int row_count = this.region_matrix.length;
   int col_count = this.region_matrix[0].length;
   
   double[] ret_array = new double[row_count*col_count];
   
   for(int i = 0; i<row_count; i++)
   {
     for(int j = 0; j<col_count; j++)
     {
       ret_array[i*col_count+j]=this.region_matrix[i][j];
     }
   }    
   return ret_array;
 }
 
 void reset_laplace_b()
 {
   for(int i = 0; i<this.laplace_b.length; i++)
   {
     this.laplace_b[i]=0;
   }
 }
 
 double[] make_laplace_b()
 {
   int row_count = this.region_matrix.length;
   int col_count = this.region_matrix[0].length;
   
   double[] ret = new double[row_count*col_count];
   return ret;
 }
 
 void reset_poisson_b(double value)
 {
   for(int i = 0; i<this.poisson_b.length; i++)
   {
     this.poisson_b[i]=value;
   }
 }
 
 double[] make_poisson_b(double value)
 {
   int row_count = this.region_matrix.length;
   int col_count = this.region_matrix[0].length;
   
   double[] ret = new double[row_count*col_count];
   for(int i = 0; i<ret.length; i++)
   {
     ret[i]=value;
   }
   
   return ret;
 }
 
 //matrix座標を入力し、その座標を境界に指定する
 void set_boundary(int x, int y)
 {
   int col_count = this.region_matrix[0].length;
   int index = col_count*y+x;    
   if(!this.boundary_index.contains(index))
   {
     this.boundary_index.add(index);
   }    
 }
 
 //matrixの外周を境界に指定(インデックスで指定)
 void set_arround_boundary()
 {
   int row_count = this.region_matrix.length;    
   int col_count = this.region_matrix[0].length;
   
   //上端
   set_row_to_boundary(0);
   //下端
   set_row_to_boundary(row_count-1);
   //左端
   set_col_to_boundary(0);
   //右端
   set_col_to_boundary(col_count-1);
 }  
 
 //領域の行単位で境界に設定する
 void set_row_to_boundary(int row_index)
 {
   int col_count = this.region_matrix[0].length;           
   for(int col_index = 0; col_index<col_count; col_index++)
   {
     set_boundary(row_index, col_index);
   }
 }
 
 //領域の列単位で境界に設定する
 void set_col_to_boundary(int col_index)
 {
   int row_count = this.region_matrix.length;  
   for(int row_index = 0; row_index<row_count; row_index++)
   {
     set_boundary(row_index, col_index);
   }
 }

 //A,bを組み立てる
 void Assembly()
 {
   int r_row_count = this.region_matrix.length;
   int r_col_count = this.region_matrix[0].length;
   
   int A_row_count = this.A.length;
   int A_col_count = this.A[0].length;
   
   this.reset_laplace_b();
   
   //xベクトル用
   int x_offset = 1;
   int y_offset = r_col_count;
   
   //xベクトルでA行列の対角を走る
   for(int i = 0; i<this.x.length; i++)
   {
     int up;
     int down;
     int left;
     int right;
     
     //xベクトル基準
     up=i-y_offset;      
     if(up<0){up=-1;}
     down=i+y_offset;
     if(x.length-1<down){down=-1;}
     left=i-x_offset;
     if(left<0){left=-1;}
     right=i+x_offset;
     if(x.length-1<right){right=-1;}
     
     if(this.boundary_index.contains(i))
     {
       this.laplace_b[i]+=this.x[i];
       this.A[i][i]=1;
       continue;
     }
     else
     {
       this.A[i][i]-=4;
     }
     
     if(0<=up)
     {       
         //up
         if(this.boundary_index.contains(up))
         {
           //ある行の方程式を成立させるために
           //bベクトルの対象行からxベクトル成分を引く
           //bベクトルは最大で４回分引かれる
           this.laplace_b[i]-=this.x[up];
         }
         else
         {
           this.A[i][up]+=1;
         }       
     }
     
     if(0<=down)
     {
         //down
         if(this.boundary_index.contains(down))
         {
           this.laplace_b[i]-=this.x[down];
         } 
         else
         {
           this.A[i][down]+=1;
         }
     }
     
     if(0<=left)
     {      
         //left
         if(this.boundary_index.contains(left))
         {
           this.laplace_b[i]-=this.x[left];
         }
         else
         {
           this.A[i][left]+=1;
         }
     }
     
     if(0<=right)
     {
         //right
         if(this.boundary_index.contains(right))
         {
           this.laplace_b[i]-=this.x[right];
         }
         else
         {
           this.A[i][right]+=1;
         }      
     }      
   }
 }
 
 //this.region_matrixに境界値を設定
 void set_row_value(int row, double value)
 {
   for(int i = 0; i<this.region_matrix[0].length; i++)
   {
     this.region_matrix[row][i]=value;
   }    
 }
 
 //this.region_matrixに境界値を設定
 void set_col_value(int col, double value)
 {
   for(int i = 0; i<this.region_matrix.length; i++)
   {
     this.region_matrix[i][col]=value;
   }        
 }
 
 //コンストラクタ
 FDM2D(int row_count, int col_count)
 {
   region_matrix = new double[row_count][col_count];

   set_row_value(0, 0);
   set_row_value(row_count-1, 0);
   set_col_value(0,0);
   set_col_value(col_count-1, 10);
   //boundary_indexの作成
   this.set_arround_boundary();
   
   this._init();
 }
 
 void _init()
 {
   int row_count = this.region_matrix.length;
   int col_count = this.region_matrix[0].length;    
   
   //A
   this.A = new double[row_count*col_count][row_count*col_count];        
   //xベクトル、全ての座標値（境界は既知、そうでなければ未知）
   this.x = make_region_array();
   //bベクトル
   this.laplace_b = make_laplace_b();
   //this.poisson_b = make_poisson_b();
   
   this.Assembly();
   this.fdm_solve();
   this.x_to_region();
 }
 
 void draw()
 {
   int row_count = this.region_matrix.length;
   int col_count = this.region_matrix[0].length; 
   
   float max = (float)max(this.region_matrix);
   
   //draw
   loadPixels();
   for(int y = 0; y < row_count; y++)
   {
     for(int x = 0; x < col_count; x++)
     {      
       //正規化
       float val = (float)this.region_matrix[y][x];  
       val = 255*(val/max);
       if(val>255){val=255;}
             
       pixels[y*w+x]=color(255-val,255-val,255-val);
     }
   }
   updatePixels();
 }
 
 int xt_offset = 20;
 int yt_offset = 20;
 
 void draw_matrix_value(double[][] mat)
 {    
   int row_count = mat.length;
   int col_count = mat[0].length; 
   
   textSize(16);
   fill(0);
   
   for(int y = 0; y < row_count; y++)
   {
     for(int x = 0; x < col_count; x++)
     {      
       double dval = mat[y][x];
       int val = (int)dval;
       String st = str(val);
       text(st,x*xt_offset,y*yt_offset, xt_offset, yt_offset);
     }
   }    
 }
 
 //Ax=b
 void fdm_solve()
 {
     double[] solved_x = solve(this.A, this.laplace_b);
     System.arraycopy(solved_x, 0, this.x, 0, solved_x.length);      
 }
 
 //xベクトルからregion_matrixへ変換
 void x_to_region()
 {
   for(int i = 0; i<this.region_matrix.length; i++)
   {
     for(int j = 0; j<this.region_matrix[0].length; j++)
     {
       this.region_matrix[i][j] = x[i*this.region_matrix[0].length+j];
     }
   }
 }
}