補間、および線形性

このページは書きかけであるが、出先からちょくちょく確認するためにここに公開される。

方程式

定義: 未知数（変数）を含む等式（=で結ばれた式）
例: $${ x + 2 = 5 }$$, $${ x^2 + y^2 = 1 }$$

同次性について、および次数と斉次（同次）

方程式の各項における次数
項の次数は、変数の指数の和で決まる。

例:
$${ x^2y }$$: 3次（$${ 2 + 1 }$$）
$${ x }$$: 1次
$${ 2xy }$$: 2次（$${ 1 + 1 }$$）
$${ 5 }$$: 0次（定数項）

同次方程式の条件
方程式に含まれる全ての項が同じ次数であること。
各項の次数（変数の指数の和）が一致している必要がある。
方程式は変数（１次以上）を含むという定義により、定数項（０次）が存在するなら必ず非同時。

例
同次方程式
$${ 2x^2y + 3xy^2 = 0 }$$ （全て3次）
$${ x + y = 0 }$$ （全て1次）

非同次方程式
$${ 2x^2y + 3xy + 1 = 0 }$$ （3次、2次、0次が混在）
$${ x + 2 = 0 }$$ （1次と0次が混在）

右辺との関係
右辺が0の場合: 同次か非同次かは、左辺の各項の次数で決まる。
右辺が非0の場合: 常に非同次方程式（右辺が定数項として扱われるため）。

各次数の一般方程式

次数を指定すると方程式の一般形が決まります：

例えば2変数$${(x,y)}$$で考えると：

2変数1次の場合の一般形（必ずしも同次でない）：

$$
ax + by + c = 0
$$

2変数2次の場合の一般形（必ずしも同次でない）：

$$
ax² + bxy + cy² + dx + ey + f = 0
$$

2変数n次（必ずしも同次でない）

$$
\sum_{i=0}^n \sum_{j=0}^{n-i} a_{ij} x^i y^j = 0
$$

この形式は必ずしも同次でない。
どちらかというと同次でない。
すなわち次数が固定されない。つまり1次2次3次の変数を作る。

この式を $${n = 0, 1, 2, 3}$$ について展開します。

---

$${n = 0}$$

$$
\sum_{i=0}^0 \sum_{j=0}^{0-i} a_{ij} x^i y^j = a_{00} x^0 y^0 = a_{00}
$$

結果:

$$
a_{00} = 0
$$

---

$${n = 1}$$

$$
\sum_{i=0}^1 \sum_{j=0}^{1-i} a_{ij} x^i y^j
$$

展開すると、

$$
\begin{aligned}
i = 0 &: \sum_{j=0}^1 a_{0j} x^0 y^j = a_{00} + a_{01} y, \\
i = 1 &: \sum_{j=0}^0 a_{1j} x^1 y^j = a_{10} x.
\end{aligned}
$$

まとめると、

$$
a_{00} + a_{01} y + a_{10} x = 0
$$

---

$${n = 2}$$

$$
\sum_{i=0}^2 \sum_{j=0}^{2-i} a_{ij} x^i y^j
$$

展開すると、

$$
\begin{aligned}
i = 0 &: \sum_{j=0}^2 a_{0j} x^0 y^j = a_{00} + a_{01} y + a_{02} y^2, \\
i = 1 &: \sum_{j=0}^1 a_{1j} x^1 y^j = a_{10} x + a_{11} xy, \\
i = 2 &: \sum_{j=0}^0 a_{2j} x^2 y^j = a_{20} x^2
\end{aligned}
$$

まとめると、

$$
a_{00} + a_{01} y + a_{02} y^2 + a_{10} x + a_{11} xy + a_{20} x^2 = 0
$$

---

$${n = 3}$$

$$
\sum_{i=0}^3 \sum_{j=0}^{3-i} a_{ij} x^i y^j
$$

展開すると、

$$
\begin{aligned}
i = 0 &: \sum_{j=0}^3 a_{0j} x^0 y^j = a_{00} + a_{01} y + a_{02} y^2 + a_{03} y^3, \\
i = 1 &: \sum_{j=0}^2 a_{1j} x^1 y^j = a_{10} x + a_{11} xy + a_{12} xy^2, \\
i = 2 &: \sum_{j=0}^1 a_{2j} x^2 y^j = a_{20} x^2 + a_{21} x^2y, \\
i = 3 &: \sum_{j=0}^0 a_{3j} x^3 y^j = a_{30} x^3
\end{aligned}
$$

まとめると、

$$
a_{00} + a_{01} y + a_{02} y^2 + a_{03} y^3 + a_{10} x + a_{11} xy + a_{12} xy^2 + a_{20} x^2 + a_{21} x^2y + a_{30} x^3 = 0
$$

---

まとめ
それぞれの $${n}$$ に対する展開は以下の通りです。

$${n = 0}$$:

$$
a_{00} = 0
$$

$${n = 1}$$:

$$
a_{00} + a_{01} y + a_{10} x = 0
$$

$${n = 2}$$:

$$
a_{00} + a_{01} y + a_{02} y^2 + a_{10} x + a_{11} xy + a_{20} x^2 = 0
$$

$${n = 3}$$:

$$
a_{00} + a_{01} y + a_{02} y^2 + a_{03} y^3 + a_{10} x + a_{11} xy + a_{12} xy^2 + a_{20} x^2 + a_{21} x^2y + a_{30} x^3 = 0
$$

2変数n次（同次）

一般化された $${ n }$$ 次の方程式：

2変数 $${ x }$$ と $${ y }$$ における $${ n }$$ 次の一般形は、次のように表されます。

$$
\sum_{k=0}^{n} a_k x^{n-k} y^k = 0
$$

この式を $${ n = 0, 1, 2, 3 }$$ で展開します。

$${ n = 0 }$$

$$
\sum_{k=0}^{0} a_k x^{0-k} y^k = a_0 x^0 y^0 = a_0 = 0
$$

$${ n = 1 }$$

$$
\sum_{k=0}^{1} a_k x^{1-k} y^k = a_0 x^{1-0} y^0 + a_1 x^{1-1} y^1 = a_0 x + a_1 y = 0
$$

$${ n = 2 }$$

$$
\sum_{k=0}^{2} a_k x^{2-k} y^k = a_0 x^{2-0} y^0 + a_1 x^{2-1} y^1 + a_2 x^{2-2} y^2
$$

$$
= a_0 x^2 + a_1 x y + a_2 y^2 = 0
$$

$${ n = 3 }$$

$$
\sum_{k=0}^{3} a_k x^{3-k} y^k = a_0 x^{3-0} y^0 + a_1 x^{3-1} y^1 + a_2 x^{3-2} y^2 + a_3 x^{3-3} y^3
$$

$$
= a_0 x^3 + a_1 x^2 y + a_2 x y^2 + a_3 y^3 = 0
$$

結果まとめ

• $${ n = 0 }$$: $${ a_0 = 0 }$$

• $${ n = 1 }$$: $${ a_0 x + a_1 y = 0 }$$

• $${ n = 2 }$$: $${ a_0 x^2 + a_1 x y + a_2 y^2 = 0 }$$

• $${ n = 3 }$$: $${ a_0 x^3 + a_1 x^2 y + a_2 x y^2 + a_3 y^3 = 0 }$$

2変数n次（基本的に同次でない（定数項を含む））

$$
\sum_{k=0}^{n} a_k x^{n-k} y^k + c = 0
$$

この場合の展開は次のようになります。

---

新しい展開式 (定数項 $${ c }$$ を含む場合)

• $${ n = 0 }$$: $${ a_0 + c = 0 }$$

• $${ n = 1 }$$: $${ a_0 x + a_1 y + c = 0 }$$

• $${ n = 2 }$$: $${ a_0 x^2 + a_1 x y + a_2 y^2 + c = 0 }$$

• $${ n = 3 }$$: $${ a_0 x^3 + a_1 x^2 y + a_2 x y^2 + a_3 y^3 + c = 0 }$$

3変数n次

解説：

3変数 $${ x, y, z }$$ の $${ n }$$ 次方程式の一般形（非同次）

一般形は以下のようになります：

$$
\sum_{i=0}^n \sum_{j=0}^{n - i} \sum_{k=0}^{n - i - j} a_{ijk} x^i y^j z^k = 0
$$

これは、各項の次数の合計が $${ n }$$ 以下であるすべての項を含みます。

$${ n = 0 }$$ の場合：

$$
\sum_{i=0}^0 \sum_{j=0}^{0} \sum_{k=0}^{0} a_{ijk} x^i y^j z^k = a_{000} x^0 y^0 z^0 = a_{000}
$$

結果：

$$
a_{000} = 0
$$

$${ n = 1 }$$ の場合：

$$
\sum_{i=0}^1 \sum_{j=0}^{1 - i} \sum_{k=0}^{1 - i - j} a_{ijk} x^i y^j z^k
$$

展開すると：

• $${ i = 0 }$$

  • $${ j = 0 }$$:

    • $${ k = 0 }$$: $${ a_{000} }$$

    • $${ k = 1 }$$: $${ a_{001} z }$$

  • $${ j = 1 }$$:

    • $${ k = 0 }$$: $${ a_{010} y }$$

• $${ i = 1 }$$

  • $${ j = 0 }$$:

    • $${ k = 0 }$$: $${ a_{100} x }$$

まとめると：

$$
a_{000} + a_{001} z + a_{010} y + a_{100} x = 0
$$

$${ n = 2 }$$ の場合：

$$
\sum_{i=0}^2 \sum_{j=0}^{2 - i} \sum_{k=0}^{2 - i - j} a_{ijk} x^i y^j z^k
$$

展開すると：

• $${ i = 0 }$$

  • $${ j = 0 }$$:

    • $${ k = 0 }$$: $${ a_{000} }$$

    • $${ k = 1 }$$: $${ a_{001} z }$$

    • $${ k = 2 }$$: $${ a_{002} z^2 }$$

  • $${ j = 1 }$$:

    • $${ k = 0 }$$: $${ a_{010} y }$$

    • $${ k = 1 }$$: $${ a_{011} y z }$$

  • $${ j = 2 }$$:

    • $${ k = 0 }$$: $${ a_{020} y^2 }$$

• $${ i = 1 }$$

  • $${ j = 0 }$$:

    • $${ k = 0 }$$: $${ a_{100} x }$$

    • $${ k = 1 }$$: $${ a_{101} x z }$$

  • $${ j = 1 }$$:

    • $${ k = 0 }$$: $${ a_{110} x y }$$

• $${ i = 2 }$$

  • $${ j = 0 }$$:

    • $${ k = 0 }$$: $${ a_{200} x^2 }$$

まとめると：

$$
\begin{aligned}
& a_{000} + a_{001} z + a_{002} z^2 + a_{010} y + a_{011} y z + a_{020} y^2 \\
& + a_{100} x + a_{101} x z + a_{110} x y + a_{200} x^2 = 0
\end{aligned}
$$

$${ n = 3 }$$ の場合：

$$
\sum_{i=0}^3 \sum_{j=0}^{3 - i} \sum_{k=0}^{3 - i - j} a_{ijk} x^i y^j z^k
$$

展開すると：

• $${ i = 0 }$$

  • $${ j = 0 }$$:

    • $${ k = 0 }$$: $${ a_{000} }$$

    • $${ k = 1 }$$: $${ a_{001} z }$$

    • $${ k = 2 }$$: $${ a_{002} z^2 }$$

    • $${ k = 3 }$$: $${ a_{003} z^3 }$$

  • $${ j = 1 }$$:

    • $${ k = 0 }$$: $${ a_{010} y }$$

    • $${ k = 1 }$$: $${ a_{011} y z }$$

    • $${ k = 2 }$$: $${ a_{012} y z^2 }$$

  • $${ j = 2 }$$:

    • $${ k = 0 }$$: $${ a_{020} y^2 }$$

    • $${ k = 1 }$$: $${ a_{021} y^2 z }$$

  • $${ j = 3 }$$:

    • $${ k = 0 }$$: $${ a_{030} y^3 }$$

• $${ i = 1 }$$

  • $${ j = 0 }$$:

    • $${ k = 0 }$$: $${ a_{100} x }$$

    • $${ k = 1 }$$: $${ a_{101} x z }$$

    • $${ k = 2 }$$: $${ a_{102} x z^2 }$$

  • $${ j = 1 }$$:

    • $${ k = 0 }$$: $${ a_{110} x y }$$

    • $${ k = 1 }$$: $${ a_{111} x y z }$$

  • $${ j = 2 }$$:

    • $${ k = 0 }$$: $${ a_{120} x y^2 }$$

• $${ i = 2 }$$

  • $${ j = 0 }$$:

    • $${ k = 0 }$$: $${ a_{200} x^2 }$$

    • $${ k = 1 }$$: $${ a_{201} x^2 z }$$

  • $${ j = 1 }$$:

    • $${ k = 0 }$$: $${ a_{210} x^2 y }$$

• $${ i = 3 }$$

  • $${ j = 0 }$$:

    • $${ k = 0 }$$: $${ a_{300} x^3 }$$

まとめると：

$$
\begin{aligned}
& a_{000} + a_{001} z + a_{002} z^2 + a_{003} z^3 + a_{010} y + a_{011} y z + a_{012} y z^2 + a_{020} y^2 \\
& + a_{021} y^2 z + a_{030} y^3 + a_{100} x + a_{101} x z + a_{102} x z^2 + a_{110} x y + a_{111} x y z \\
& + a_{120} x y^2 + a_{200} x^2 + a_{201} x^2 z + a_{210} x^2 y + a_{300} x^3 = 0
\end{aligned}
$$

3変数の同次方程式の場合

同次の場合、各項の次数の合計が常に $${ n }$$ になります。

一般形：

$$
\sum_{i=0}^n \sum_{j=0}^{n - i} a_{ij} x^i y^j z^{n - i - j} = 0
$$

$${ n = 0 }$$ の場合：

$$
a_{00} x^0 y^0 z^0 = a_{00} = 0
$$

$${ n = 1 }$$ の場合：

$$
a_{00} x^1 y^0 z^0 + a_{01} x^0 y^1 z^0 + a_{02} x^0 y^0 z^1 = a_{00} x + a_{01} y + a_{02} z = 0
$$

$${ n = 2 }$$ の場合：

$$
\begin{aligned}
& a_{00} x^2 + a_{01} x y + a_{02} x z + a_{10} y^2 + a_{11} y z + a_{20} z^2 = 0
\end{aligned}
$$

ただし、この場合は $${ i + j + k = n }$$ を満たす全ての組合せについて $${ a_{ijk} x^i y^j z^k }$$ を取ります。

$${ n = 3 }$$ の場合：

$$
\begin{aligned}
& a_{000} x^3 + a_{001} x^2 y + a_{002} x^2 z + a_{010} x y^2 + a_{011} x y z + a_{020} x z^2 \\
& + a_{100} y^3 + a_{101} y^2 z + a_{110} y z^2 + a_{200} z^3 = 0
\end{aligned}
$$

定数項を含む場合（非同次の一般形）

定数項 $${ c }$$ を含めた一般形は以下のようになります：

$$
\sum_{i=0}^n \sum_{j=0}^{n - i} \sum_{k=0}^{n - i - j} a_{ijk} x^i y^j z^k + c = 0
$$

$${ n = 0 }$$ の場合：

$$
a_{000} + c = 0
$$

$${ n = 1 }$$ の場合：

$$
a_{000} + a_{001} z + a_{010} y + a_{100} x + c = 0
$$

$${ n = 2 }$$ の場合：

先ほどの $${ n = 2 }$$ の展開に $${ c }$$ を加えます：

$$
\begin{aligned}
& a_{000} + a_{001} z + a_{002} z^2 + a_{010} y + a_{011} y z + a_{020} y^2 \\
& + a_{100} x + a_{101} x z + a_{110} x y + a_{200} x^2 + c = 0
\end{aligned}
$$

$${ n = 3 }$$ の場合：

同様に $${ c }$$ を加えます：

$$
\begin{aligned}
& a_{000} + a_{001} z + a_{002} z^2 + a_{003} z^3 + a_{010} y + a_{011} y z + a_{012} y z^2 + a_{020} y^2 \\
& + a_{021} y^2 z + a_{030} y^3 + a_{100} x + a_{101} x z + a_{102} x z^2 + a_{110} x y + a_{111} x y z \\
& + a_{120} x y^2 + a_{200} x^2 + a_{201} x^2 z + a_{210} x^2 y + a_{300} x^3 + c = 0
\end{aligned}
$$

まとめ：

• 3変数の場合でも、次数 $${ n }$$ に対して一般形を展開できます。

• 非同次の一般形では、次数の合計が $${ n }$$ 以下の全ての項を含みます。

• 同次方程式では、各項の次数の合計が常に $${ n }$$ になります。

• 定数項を含む場合は、展開した式に $${ c }$$ を加えます。

これで3変数の場合の展開が完了しました。何か他にご質問があれば、お知らせください。

m変数n次

---

解説：

$${ m }$$ 変数の $${ n }$$ 次方程式の一般形（非同次）

$${ m }$$ 個の変数 $${ x_1, x_2, \dots, x_m }$$ に対する $${ n }$$ 次の一般形は以下のように表されます：

$$
\sum_{k=0}^n \sum_{\substack{i_1, i_2, \dots, i_m \geq 0 \\ i_1 + i_2 + \dots + i_m = k}} a_{i_1 i_2 \dots i_m} x_1^{i_1} x_2^{i_2} \dots x_m^{i_m} = 0
$$

この式は、各項の変数の指数の和が $${ n }$$ 以下であるすべての組み合わせについての総和を表しています。

読み方は$${ k }$$ が $${ 0 }$$ から $${ n }$$ まで動く場合の総和について、さらにその中で $${ m }$$ 個の添字 $${ i_1, i_2, \dots, i_m }$$ が $${ 0 }$$ 以上の整数であり、かつ $${ i_1 + i_2 + \dots + i_m = k }$$ を満たす条件での総和をとる。

コードだと

from itertools import product

def compute_sum(n, m, a, x):
    """
    Parameters:
        n (int): 最大の k の値
        m (int): 変数の数
        a (dict): a[i1, i2, ..., im] の係数を格納する辞書
        x (list): [x1, x2, ..., xm] のリスト
    Returns:
        result (float): 式の値
    """
    result = 0
    for k in range(n + 1):  # k = 0 から n
        for indices in product(range(k + 1), repeat=m):  # 全組み合わせを生成
            if sum(indices) == k:  # 条件 i1 + i2 + ... + im = k を確認
                term = a.get(indices, 0)  # 該当の係数 a[i1, i2, ..., im] を取得
                for i, xi in zip(indices, x):
                    term *= xi ** i  # 各変数のべき乗を掛け算
                result += term
    return result

# 使用例
n = 2
m = 2
a = {
    (0, 0): 1,
    (1, 0): -2,
    (0, 1): 3,
    (1, 1): 4,
    (2, 0): -1,
    (0, 2): 2,
}
x = [1, 2]  # x1 = 1, x2 = 2

result = compute_sum(n, m, a, x)
print("結果:", result)

具体例：

$${ n = 0 }$$ の場合：

$$
\sum_{\substack{i_1, i_2, \dots, i_m \geq 0 \ i_1 + i_2 + \dots + i_m = 0}} a_{i_1 i_2 \dots i_m} x_1^{i_1} x_2^{i_2} \dots x_m^{i_m} = a_{0 0 \dots 0} = 0
$$

結果：

$$
a_{0 0 \dots 0} = 0
$$

$${ n = 1 }$$ の場合：

指数の和が 1 になる組み合わせは、各変数について指数が 1 で他は 0 の場合です。

$$
\sum_{\substack{i_1 + i_2 + \dots + i_m = 1 \ i_j \geq 0}} a_{i_1 i_2 \dots i_m} x_1^{i_1} x_2^{i_2} \dots x_m^{i_m} = 0
$$

展開すると：

$$
a_{1 0 \dots 0} x_1 + a_{0 1 \dots 0} x_2 + \dots + a_{0 0 \dots 1} x_m + a_{0 0 \dots 0} = 0
$$

$${ n = 2 }$$ の場合：

指数の和が 0, 1, 2 となるすべての組み合わせを考えます。

• 和が 0 の場合：$${ a_{0 0 \dots 0} }$$

• 和が 1 の場合：$${ a_{1 0 \dots 0} x_1, a_{0 1 \dots 0} x_2, \dots, a_{0 0 \dots 1} x_m }$$

• 和が 2 の場合：二次の項

二次の項は以下のようになります：

• $${ x_1^2 }$$ の項：$${ a_{2 0 \dots 0} x_1^2 }$$

• $${ x_1 x_2 }$$ の項：$${ a_{1 1 0 \dots 0} x_1 x_2 }$$

• すべての変数の組み合わせについて同様に考えます。

一般的に、指数の和が 2 になるすべての $${ i_1, i_2, \dots, i_m }$$ の組み合わせについて総和を取ります。

$${ m }$$ 変数の $${ n }$$ 次同次方程式の場合

同次方程式では、各項の変数の指数の和が常に $${ n }$$ になります。

一般形は以下のようになります：

$$
\sum_{\substack{i_1, i_2, \dots, i_m \geq 0 \ i_1 + i_2 + \dots + i_m = n}} a_{i_1 i_2 \dots i_m} x_1^{i_1} x_2^{i_2} \dots x_m^{i_m} = 0
$$

具体例：

$${ n = 0 }$$ の場合：

$$
a_{0 0 \dots 0} = 0
$$

$${ n = 1 }$$ の場合：

$$
a_{1 0 \dots 0} x_1 + a_{0 1 \dots 0} x_2 + \dots + a_{0 0 \dots 1} x_m = 0
$$

$${ n = 2 }$$ の場合：

指数の和が 2 になるすべての組み合わせについて考えます。

• $${ x_1^2 }$$ の項：$${ a_{2 0 \dots 0} x_1^2 }$$

• $${ x_1 x_2 }$$ の項：$${ a_{1 1 0 \dots 0} x_1 x_2 }$$

• $${ x_1 x_3 }$$ の項：$${ a_{1 0 1 \dots 0} x_1 x_3 }$$

• 以降、すべての組み合わせについて同様に展開します。

定数項を含む場合（非同次の一般形）

定数項 $${ c }$$ を含める場合、一般形は以下のようになります：

$$
\sum_{k=0}^n \sum_{\substack{i_1 + i_2 + \dots + i_m = k \ i_j \geq 0}} a_{i_1 i_2 \dots i_m} x_1^{i_1} x_2^{i_2} \dots x_m^{i_m} + c = 0
$$

具体例：

$${ n = 0 }$$ の場合：

$$
a_{0 0 \dots 0} + c = 0
$$

$${ n = 1 }$$ の場合：

$$
a_{0 0 \dots 0} + a_{1 0 \dots 0} x_1 + a_{0 1 \dots 0} x_2 + \dots + a_{0 0 \dots 1} x_m + c = 0
$$

一般的な形の説明

$${ m }$$ 変数の $${ n }$$ 次方程式では、各項は次の形になります：

• 変数の指数の和が $${ n }$$ 以下（非同次の場合）または $${ n }$$（同次の場合）となるすべての組み合わせについて、係数 $${ a_{i_1 i_2 \dots i_m} }$$ と対応する変数の積 $${ x_1^{i_1} x_2^{i_2} \dots x_m^{i_m} }$$ を取ります。

• 各 $${ i_j }$$ は 0 以上の整数です。

注意点

• 変数の数 $${ m }$$ や次数 $${ n }$$ が大きくなると、項の数が急速に増加します。

• 総和の範囲や条件を明確に指定することで、一般形を正確に表現できます。

---

まとめ：

• $${ m }$$ 変数の場合でも、同様の方法で $${ n }$$ 次方程式の一般形を展開できます。

• 非同次の一般形では、変数の指数の和が $${ n }$$ 以下となるすべての項を含みます。

• 同次方程式では、各項の変数の指数の和が常に $${ n }$$ になります。

• 定数項を含める場合は、式の末尾に $${ c }$$ を加えます。

何か他にご質問があれば、お知らせください。

二次形式（m変数2次）

次数は2
m変数2次。

二次形式（quadratic form）とは、数学において、ベクトルの集合に対して特定の形で値を与える多項式の一種で、特に2次の項だけを持つ形式のことを指します。

具体的には、二次形式は次のように定義されます。

---

定義
$${ m }$$-次元ベクトル $${\mathbf{x} = (x_1, x_2, \dots, x_m)^T }$$ に対して、二次形式 $${ Q(\mathbf{x}) }$$ は以下のように表されます：

$$
Q(\mathbf{x}) = \mathbf{x}^T A \mathbf{x},
$$

ここで：

• $${ A }$$ は $${ m \times m }$$ の実対称行列（または複素エルミート行列）。

• $${\mathbf{x}^T}$$ はベクトル $${\mathbf{x}}$$ の転置。

展開すると、二次形式は次のようになります：

$$
Q(\mathbf{x}) = \sum_{i=1}^m \sum_{j=1}^m a_{ij} x_i x_j,
$$

ただし、行列 $${ A = [a_{ij}] }$$ の成分を用いています。

---

例
1変数の場合：

$$
Q(x) = ax^2
$$

（ここでは $${ A }$$ は $${ 1 \times 1 }$$ の行列 $${ [a] }$$）。

2変数の場合：

$$
Q(x_1, x_2) = a_{11}x_1^2 + 2a_{12}x_1x_2 + a_{22}x_2^2,
$$

（行列 $${ A }$$ は次のようになります：

$$
A = \begin{bmatrix} a_{11} & a_{12} \\
a_{12} & a_{22} \end{bmatrix}.
$$

---

性質と応用
正定値性と負定値性：

• 二次形式 $${ Q(\mathbf{x}) > 0 }$$ がすべての $${\mathbf{x} \neq 0}$$ に対して成立する場合、行列 $${ A }$$ は正定値。

• 同様に、$${ Q(\mathbf{x}) < 0 }$$ ならば $${ A }$$ は負定値。

幾何学的応用：
二次形式は、楕円体や放物面、双曲面などの二次曲面を表現する際に用いられます。

機械学習・統計学：
二次形式は、ガウス分布の共分散行列や主成分分析（PCA）など、多くの統計モデルで中心的役割を果たします。

最適化：
二次計画問題（quadratic programming）において、コスト関数として現れます。

---

以下に、ベクトル $${\mathbf{x}}$$ が次元 $${m=0, 1, 2, 3}$$ の場合について、二次形式 $${Q(\mathbf{x}) = \mathbf{x}^T A \mathbf{x}}$$ を展開していきます。

---

$${m = 0}$$ の場合
$${\mathbf{x}}$$ は空ベクトル（$${\mathbf{x} = []}$$）で、$${A}$$ は $${0 \times 0}$$ の空行列です。この場合、二次形式 $${Q(\mathbf{x})}$$ は定義上 0 です。
$$
Q(\mathbf{x}) = 0
$$

---

$${m = 1}$$ の場合
$${\mathbf{x} = [x_1]}$$ （1次元ベクトル）
$${A = [a_{11}]}$$ （$${1 \times 1}$$ の行列）

二次形式は次のようになります：
$$
Q(\mathbf{x}) = \mathbf{x}^T A \mathbf{x} = [x_1] \cdot [a_{11}] \cdot [x_1] = a_{11}x_1^2
$$

結果：
$$
Q(\mathbf{x}) = a_{11}x_1^2
$$

---

$${m = 2}$$ の場合
$${\mathbf{x} = [x_1, x_2]^T}$$ （2次元ベクトル）
$$
A = \begin{bmatrix}
a_{11} & a_{12} \
a_{12} & a_{22}
\end{bmatrix} \quad (\text{$${A}$$ は対称行列と仮定})
$$

二次形式は次のように展開されます：
$$
Q(\mathbf{x}) = \mathbf{x}^T A \mathbf{x} = [x_1, x_2] \cdot
\begin{bmatrix}
a_{11} & a_{12} \
a_{12} & a_{22}
\end{bmatrix}
\cdot
\begin{bmatrix}
x_1 \
x_2
\end{bmatrix}
$$

計算すると：
$$
Q(\mathbf{x}) = a_{11}x_1^2 + 2a_{12}x_1x_2 + a_{22}x_2^2
$$

結果：
$$
Q(\mathbf{x}) = a_{11}x_1^2 + 2a_{12}x_1x_2 + a_{22}x_2^2
$$

---

$${m = 3}$$ の場合
$${\mathbf{x} = [x_1, x_2, x_3]^T}$$ （3次元ベクトル）
$$
A = \begin{bmatrix}
a_{11} & a_{12} & a_{13} \
a_{12} & a_{22} & a_{23} \
a_{13} & a_{23} & a_{33}
\end{bmatrix}
\quad (\text{$${A}$$ は対称行列と仮定})
$$

二次形式は次のように展開されます：
$$
Q(\mathbf{x}) = \mathbf{x}^T A \mathbf{x} = [x_1, x_2, x_3] \cdot
\begin{bmatrix}
a_{11} & a_{12} & a_{13} \
a_{12} & a_{22} & a_{23} \
a_{13} & a_{23} & a_{33}
\end{bmatrix}
\cdot
\begin{bmatrix}
x_1 \
x_2 \
x_3
\end{bmatrix}
$$

計算すると：
$$
Q(\mathbf{x}) = a_{11}x_1^2 + 2a_{12}x_1x_2 + 2a_{13}x_1x_3 + a_{22}x_2^2 + 2a_{23}x_2x_3 + a_{33}x_3^2
$$

結果：
$$
Q(\mathbf{x}) = a_{11}x_1^2 + a_{22}x_2^2 + a_{33}x_3^2 + 2a_{12}x_1x_2 + 2a_{13}x_1x_3 + 2a_{23}x_2x_3
$$

---

まとめ

• $${m=0}$$: $${Q(\mathbf{x}) = 0}$$

• $${m=1}$$: $${Q(\mathbf{x}) = a_{11}x_1^2}$$

• $${m=2}$$: $${Q(\mathbf{x}) = a_{11}x_1^2 + 2a_{12}x_1x_2 + a_{22}x_2^2}$$

• $${m=3}$$: $${Q(\mathbf{x}) = a_{11}x_1^2 + a_{22}x_2^2 + a_{33}x_3^2 + 2a_{12}x_1x_2 + 2a_{13}x_1x_3 + 2a_{23}x_2x_3}$$

基底

・ベクトルは２つ足すと別のベクトルになる。
・ベクトルは定数倍すると伸び縮みする。

たいがいのベクトルは、基準となるベクトルに係数を掛け、それらを足し合わせることで表現できる。その時、基準となるベクトルのことを基底という。

基底は基本的には適当に決めて良いが、最も標準的な基底のことを標準基底という。例えば２次元空間ならば(1,0)(0,1)なる２つのベクトル。３次元ベクトルなら(1,0,0)(0,1,0)(0,0,1)なる３つのベクトルが標準基底にあたる。

Fig A

基底のちゃんとした定義はwikipediaに書いてあるが

式(1.0)

なるを満たすに、全てのaがゼロでなければ成立しないようなベクトルのことを線形独立といい、基底とはそれの集まりである。

で、あるからして。基底であることと直交している（内積ゼロ）とか、長さが１とかとは別の話である。標準基底は正規直交基底（長さ１、内積ゼロ、互いに独立）である。

この基底の独立性というのがどれくらいの縛りかといえば、例えば二次元空間はただの２つの二次元基底ベクトルをこねくり回すことだけで表現することが可能になるが、逆にどれだけこねくり回しても三次元ベクトルは構築できないというレベルの縛りである。

線形性

$${\mathbb R^n}$$の全てのベクトルと
全てのスカラーcに関して以下のような操作ができること。

加法性
$${f(\mathbf x_1+\mathbf x_2)=f(\mathbf x_1)+f(\mathbf x_2)}$$

斉次性
$${f(c\mathbf x)=cf(\mathbf x)}$$

直交性

上の図Aの場合、ベクトル(1,0)とベクトル(1,1)は内積すると1。つまり直交してない。
式(1.0)はa1,a2,a3…を組としてベクトル（ないし1行or1列の行列)
v1,v2,v3…の各ベクトルを組としてベクトル（ないし1行or1列の行列)
を成せばこれらの積の総和（内積）の結果は０であるから直交している。
数値であるとかベクトルであるとか、関数であるとかは抽象化され、それらの組み合わせや変換の規則の方がよっぽど問題になる。その一つの例が内積。

また、区間[a,b]において区分的に連続な実数値関数f(x),g(x)がある時、

$$
(f,g)=\int_a^bf(x)g(x)dx
$$

をf(x)とg(x)の内積という。これはフーリエ級数とかで出てくる。

線形独立と線形結合

他を生み出す基準となるようなものに係数掛けて全部足せば他の大体のもんは生成できる。こんなようなことは関数でもできる。すなわち他の基準となるような関数に係数掛けて足せば、他の大体の関数は表現できる。こんなような要領のことごとを線形結合という。

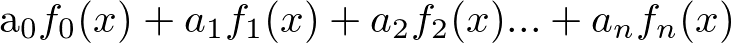
よく使われるのが以下の多項式(polynomial)

あるいは三角多項式(trigonometric polynomial)

微分方程式の場合、道関数yとその導関数

についての1次式

なるをn階1次の線形微分方程式という。
とくにQ(x)=0の時を斉次（同次）という。
Q(x)≠0の時、Q(x)の項の次数が0なので斉次にならない（と、思われる）。
物理的には保存則（微分=0、ゆえに量の変化なし）に相当。
Q(x)≠0の時、系に外力が加わっている状態。

補間

補間というのは、情報が足らない時に、その情報のスキマを関数で埋めてしまうことである。

例えば１００×１００ピクセルの画像を２００×２００ピクセルに拡大した場合、拡大後の画像を構築するには元の画像の４倍の情報量が必要である。しかしこの拡大後画像を構築するための材料は元のちっこい画像しかない。そういう時に補間が必要になる。

例えば観測値から規則性を見出す場合も補間が使われるであろう。昨日の昼間の気温と明日の昼間の気温が分かっていれば、今日の昼間の気温を求めるに大概の人は足して２で割る。昨日と今日の気温が分かれば明日の気温も予測できる。データが増え、求めたい日時を自由に選択したければ観測された値のスキマを関数で補完することになる。

例えば少ないポリゴンから、ポリポリしないグラフィックを生成するには補間を用いたシェーディングが利用される。この場合はポリゴンの頂点に色情報がヒモ付られており、頂点が作る線なり面なりの色は補間によって決定される。多分。

こんな塩梅であるので、統計、ＡＩ、有限要素法、曲線描画、いろんなところで補完は顔を出す。

線形補間(linear interpolation, lerp)

参考
数値計算法 (電子通信学会大学シリーズ A- 4) (日本語) 単行本 – 1981/1/1
戸川 隼人 (著)　p13

複数点間を線形に補間。

二点(x0,y0)(x1,y1)間を補間。

二次補間

補間が待たれる。

三次補間

補間が待たれる。

多項式補間(polynomial interpolation)

補間が待たれる。

ラグランジュ補間

https://note.com/alchan/n/n885679f398c8

ニュートン補間

https://note.com/alchan/n/nc14a3c453144

ニュートン基底関数

その例

ニュートン基底関数に掛かる係数

括弧付きは差商と呼ばれるもの、以下その例

エルミート補間

スプライン補間