[3D]一点透視図を極めんとする者～無限遠点に向かって走れの巻～

このページは研究中のものです。

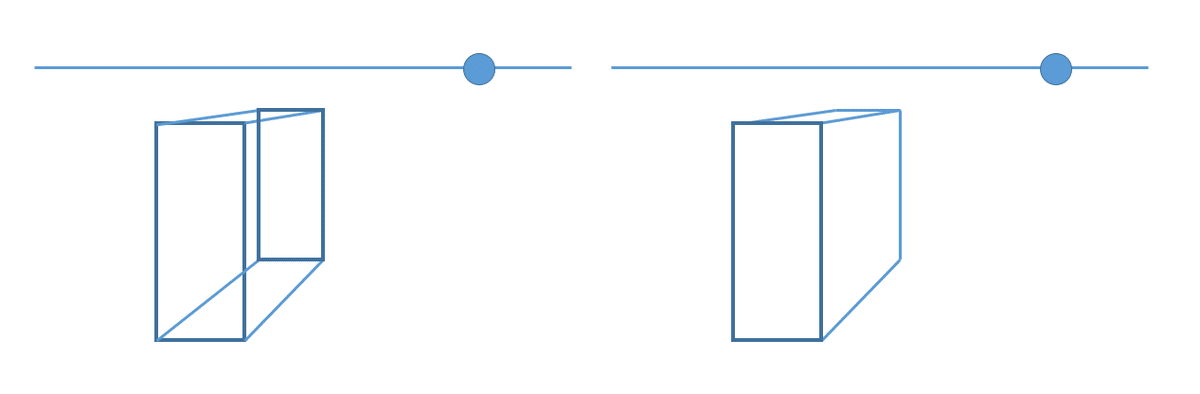
以下のようなヤツを３Ｄ関連のAPI使わずに作りたい。

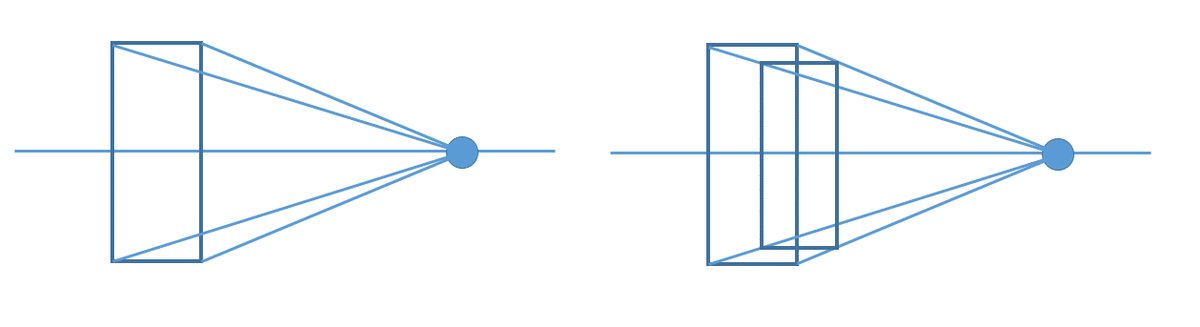
適当なパラメータtで作る場合。

各座標から消失点にベクトルを射出し、あるいは消失点から各座標にベクトルを射出し、t値でそのベクトルを切る。このやり方はカメラ情報どころか建物の奥行情報（ｚ座標）すらいらなきもの。

必要なのはパースを掛けたい箱の前面のx,y座標（上図の場合、４つ頂点のx,y）
適当な消失点のx,y座標
適当なパラメータt（０～１が望ましい）
出力はパースの効いた箱の前面以外の座標

利点：楽
難点：雑

//疑似コード
List<Vector2D> Box = FrontVertices.Copy();
for(int i = 0; i<this.FrontVertices.Length; i++)
{
    Vector2D v = this.FrontVertices[i];
    Vector2D persed_v = v+(Vanish-v)*t;    Box.add(persed_v);
}

ピンホールカメラモデルを用いる場合。

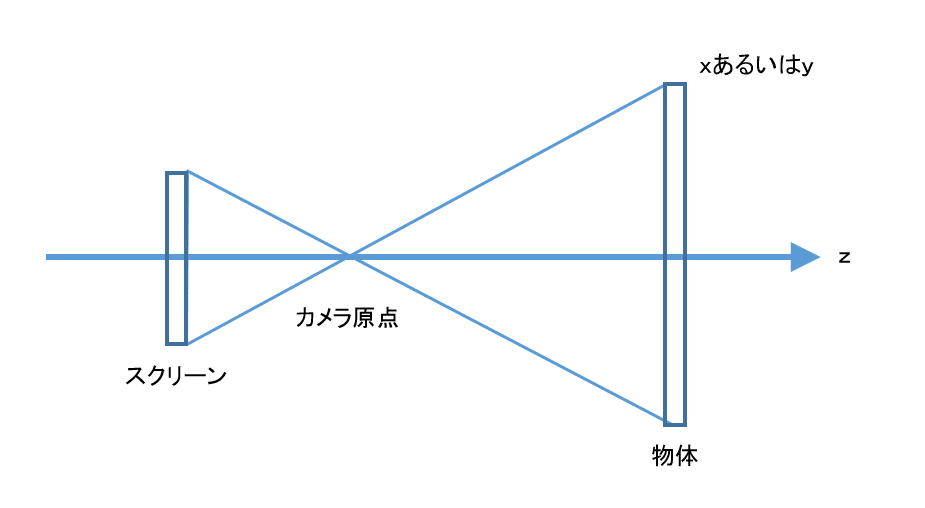
ピンホールカメラは像がひっくり返るが、ひっくり返さない方が便利なので以下のように考えて

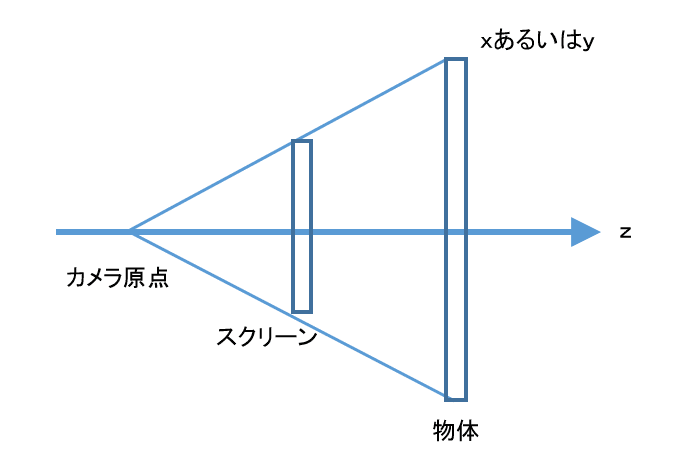
このモデルの場合、同じ大きさの物体でもカメラから遠い方がスクリーンに映る像は小さい

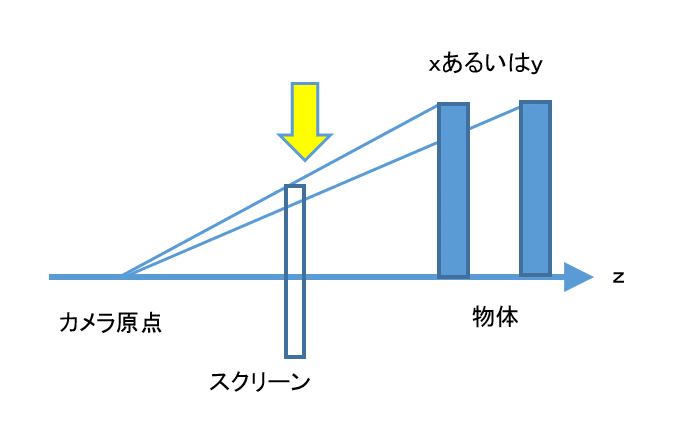
このことは以下のような式で表されるが、結局のところ、ベクトルをt値で切るやつとやってることはそんなに違わない。

$$
\frac{1}{z}=t
$$

である。

//遠い方(zが大きい)のが小さく見えるの式
x'=x/z;
y'=y/z;

カメラからスクリーンまでの距離dを考慮に入れる場合

x'=d*(x/z);
y'=d*(y/z);

これらの式は
ある座標(x,y,z)と投影面上の座標(x',y',d)の比によって導かれる

$$
\frac{x'}{x}=\frac{y'}{y}=\frac{d}{z}
$$

$$
x'=\frac{xd}{z}\\
y'=\frac{yd}{z}
$$

カメラとスクリーンの距離dが大きいということは、空間中の座標の方に向かってスクリーンを押し付けているわけだから、スクリーンに映る座標は、カメラとスクリーンの距離dが大きいほど巨大な座標となる。

注意として、この式に現れる座標値x,y,zは全てカメラ座標系であることである。例えば以下のような３Ｄ箱の座標があるとして、

 Vector3D V1 = new Vector3D(100,100,1);
 Vector3D V2 = new Vector3D(200,100,1);
 Vector3D V3 = new Vector3D(200,200,1);
 Vector3D V4 = new Vector3D(100,200,1);  
 Vector3D V5 = new Vector3D(100,100,10);
 Vector3D V6 = new Vector3D(200,100,10);
 Vector3D V7 = new Vector3D(200,200,10);
 Vector3D V8 = new Vector3D(100,200,10);  

各々の(x,y)をバカ正直にzで除すると、(x,y)はスクリーン座標の左上原点(0,0)に収束する。

なので消失点に収束させたければ(x,y)はカメラ系に変換しなければならない。後述するが一点透視では消失点(x,y)とカメラ位置(x,y)は同じと考えて良い。消失点に収束=カメラ系に変換となるのはこのため。

 //Processing
 for(int i = 0; i<this.Vertices.size(); i++)
 {
   PVector v = this.Vertices.get(i).copy();
   
   //これはスクリーン座標の左上原点に収束する
   //float nx = (v.x)/(v.z);
   //float ny = (v.y)/(v.z);  

   float nx = Vanish.x+((v.x-Vanish.x)/(v.z));
   float ny = Vanish.y+((v.y-Vanish.y)/(v.z));  
 }

float nx = Vanish.x+((v.x-Vanish.x)/(v.z));
ここで
Vanish.x：カメラ系の原点
v.x-Vanish.x：ワールド系→カメラ系の変換、平行移動処理
((v.x-Vanish.x)/(v.z))：カメラ系座標のパース処理
((v.x-Vanish.x)/(v.z-Vanish.z))：カメラのz座様が0以外の場合

カメラの位置（カメラ系の原点、消失点）＋カメラ系の座標
はスクリーン座標系の座標となる。

ベクトルのt値切断と違うのは
箱の全てのx,y,z座標（最初の図の場合、８頂点のx,y,z）が必要。
適当なカメラ（消失点）のx,y座標が必要。
必用ならカメラ（消失点）のz座標が必要。

最初のt値切断は全てのz値をいっしょくたにしたものであり、逆に言えばt値を全ての頂点に対して用意すればやってることはさして変わらなくなる。

三角比使う場合。

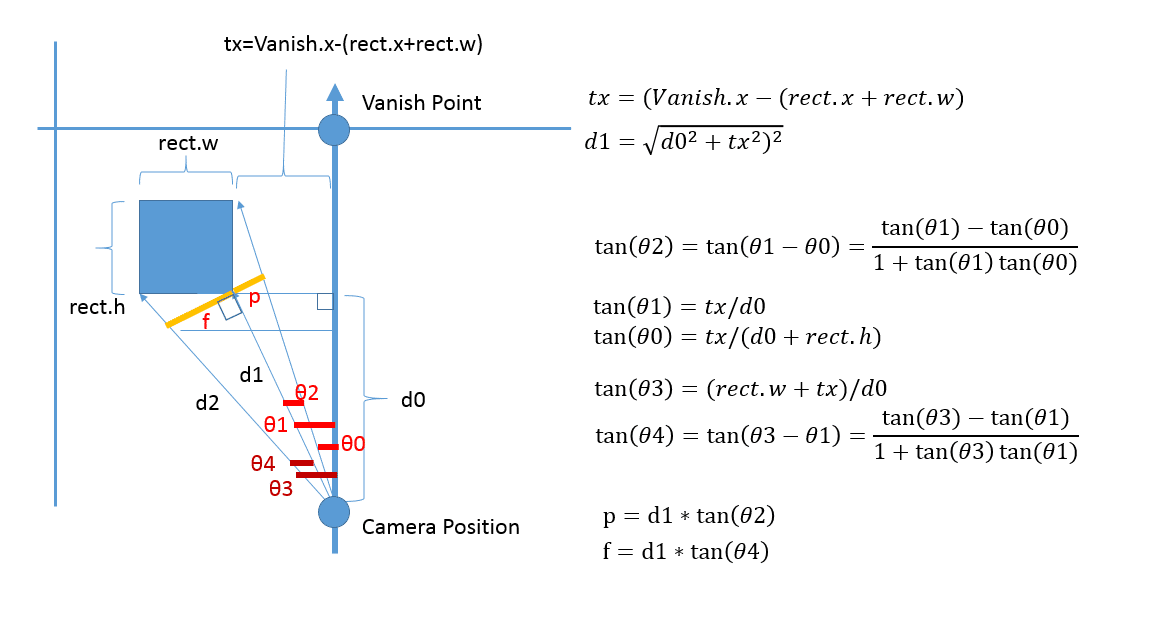
箱の全ての座標（ワールド系でもカメラ系でも良いが、多分カメラ系にした方が最終的には楽）、消失点(x,y)、カメラ位置(z)なるパラメータが全て既知であること。スクリーン表示時には全ての頂点にパースがかかる。

ここで例えば、rect.wが既にスクリーン上で表示されており、これが例えばrect.w=100であって、100Pixelの描画は変更したくない場合、奥行きは

w'=w*f/p;

となる。これはおそらくカメラ位置の自動補正のような機能を持つ。

ここに至るに必要パラメータにカメラ位置が姿を現した。カメラ軸はまだない。なぜなら一点透視図であるから。
難点：試してない。

視錐台使う場合。

箱の全ての座標、カメラ位置、カメラ軸（ピッチ、ヨー、ロール）、視錐台にかかる全てのパラメータ（視野角、前方クリップ面までの距離、後方クリップ面までの距離）が必要になる。

一点透視図は必ずしも維持されない
消失点の概念はカメラのパラメータに吸収される。
一点透視図とはワールド系の(x,y,z)軸ならびにカメラ系の(x,y,z)軸が全て平行な時である。
二点透視図とはワールド系の(x,y,z)軸ならびにカメラ系の(x,y,z)軸のうち、y軸のみ平行な時である。
三点透視図とはワールド系の(x,y,z)軸ならびにカメラ系の(x,y,z)軸のうち、全ての軸が平行でない時である。

詳細はまたその内別のページでしるす。気になる方は自分で試しても良い。
https://note.com/alchan/n/na643a93f41f9

利点：既存のＡＰＩが完全に実装してくれている。
難点：パラメータ多い。

また、消失点を中心に、とか。いまあるビルの幅を基準に、とかいう方向から考えた場合、多分コンピュータービジョン的な要素が入ってきて逆行列使わなかんなる。気がする。

陰面消去

さて、自前でパースをごにゃごにゃする場合、めんどくさいのは座標値よりもむしろ陰面消去である。

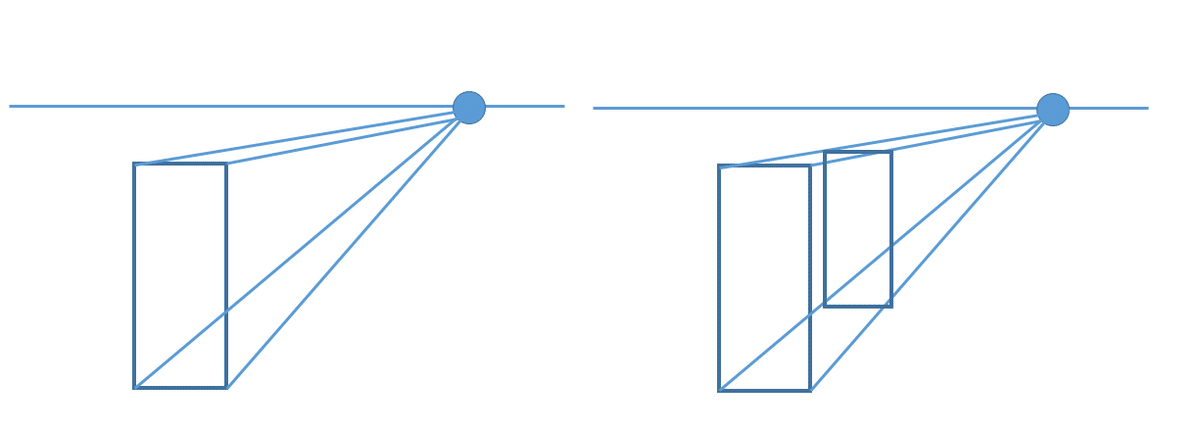
なに基準で表示する線、しない線を決めるのかと。

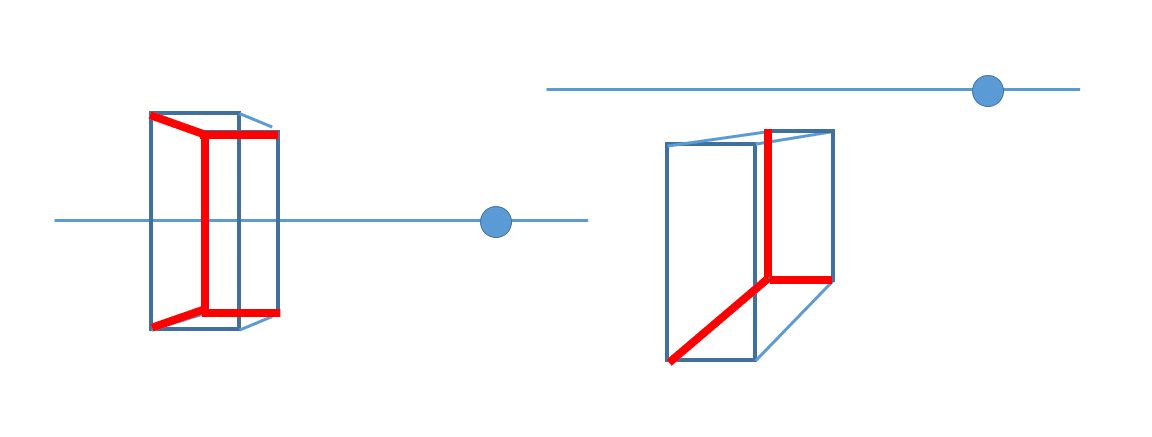
ここでは自分で勝手に作ったアルゴリズムを用いた。ひょっとしたら先人がいるやもしれぬ。というか、多分おる。

・まず箱を、前面、前面を奥に押し出した背面、それらの頂点を繋ぐ線で考える。
・前面と背面の凸包をとり、塗りつぶす。
・頂点繋ぎ線のうち、前面と衝突しないもののみ描画する。
・前面を塗りつぶす。

凸包
https://note.com/alchan/n/nba38ef9649c3

頂点繋ぎ線と前面の衝突は、端点を含まない線分交差判定を用いる。端点を含む交差判定だと、頂点同士が接しているので常にTrueになってしまう。
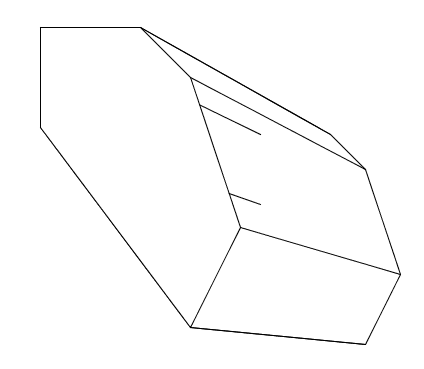
また、この衝突判定自体をしないでいると、前面からはみ出た部分は塗り潰されずに描画されてしまう（下図）。

ジャンル的には消失点からの二次元レイトレーシング的なことであろう。

線分の交差判定は
https://note.com/alchan/n/n740dfc548638
https://note.com/alchan/n/nb2370bc28a25

t値でベクトル切るやつ

ArrayList<PVector> GetPerse(ArrayList<PVector> source, PVector vanish_point, float t)
{
 ArrayList<PVector> ret = new ArrayList<PVector>();
 
 for(PVector v : source)
 {
   PVector from_v = vanish_point.copy().sub(v);
   PVector lv = v.copy().add(from_v.mult(t));
   ret.add(lv);
 }
 return ret;
}

元になる頂点から適当なパース後頂点をもとめ、おもむろに描画する。

  ArrayList<PVector> persed = GetPerse(Poly,Vanish,0.3);   
  DrawWall(Poly, persed, this.Vanish);

ここで使用する凸包作成は入力した座標を破壊するので注意を要する。例えば以下でsourceのQuickHullを求めると、sourceは破壊される。破壊されると困るなら先にコピーすること。

void DrawWall(ArrayList<PVector> source, ArrayList<PVector> parse, PVector vanish_point)
{
 ArrayList<PVector> total_convex = new ArrayList<PVector>();
 for(PVector p : source){total_convex.add(p.copy());}
 for(PVector p : parse){total_convex.add(p.copy());}
 total_convex =QuickHull(total_convex);
 
 FillLinerClose(total_convex);//前面と背面の凸包塗りつぶし
 for(int i = 0; i<source.size(); i++)
 {
   PVector p = source.get(i).copy();
   if(!(IsInsideIntersect(new VectorLine2D(p,vanish_point),source)))
   {
     //頂点繋ぎ線
     DrawLine(source.get(i),parse.get(i));
   }        
 }
 FillLinerClose(source);//前面の塗りつぶし
 }

IsInsideIntersectが前面と頂点繋ぎ線の衝突判定である。

//lineは多角形と交差するか
//凸限定
public boolean IsInsideIntersect(VectorLine2D line1, ArrayList<PVector> poly)
{
 for(int i = 0; i<poly.size(); i++)
 {
   PVector v0 = poly.get(i).copy();
   PVector v1 = poly.get((i+1)%poly.size()).copy();
   VectorLine2D line2 = new VectorLine2D(v0,v1);
   
   if(IsInsideIntersect(line1,line2))
   {
     return true;
   }    
 }
 return false;
}

//端点を判定から除外する
public boolean IsInsideIntersect(VectorLine2D l1, VectorLine2D l2)
{
 if (IsStraddle(l1, l2))
 {
   if (IsStraddle(l2, l1))
   {
     return true;
   }
 }
 return false;
}


//端点を判定に含まない
//Straddleは交差判定の部品であって交差判定ではない
//片方が片方が跨ぐか否か
//交差判定は線分がお互いにStraddleを判定する
public boolean IsStraddle(VectorLine2D l1, VectorLine2D l2)
{
 PVector lv1 = l1.LV();
 PVector l1SVtol2SV = PVector.sub(l2.SV, l1.SV);
 PVector l1SVtol2EV = PVector.sub(l2.EV, l1.SV);

 //OnLineはとらない(false)
 if ((int)Cross(lv1, l1SVtol2SV) == 0 || (int)Cross(lv1, l1SVtol2EV) == 0)
 {
   return false;
 }
 //これだけだとOnLineをとってしまうことがある
 if (((int)Cross(lv1, l1SVtol2SV) ^ (int)Cross(lv1, l1SVtol2EV)) < 0)
 {
   return true;
 }
 return false;
}