Wikipediaに書いてあることをそのまま解説したCohen–Sutherland algorithm

Cohen窶鉄utherland algorithm - Wikipedia

線分を矩形でちょん切るアルゴリズム。

線分を構成する２つの端点が、矩形に対して各々どこに位置するかを考えます。その後２つの端点の位置に応じてあれやこれやと処理します。

矩形はディスプレイ画面を９分割すると考えます。分割した領域に応じてビットを割り当てます。例えばwikipediaの例にならうと

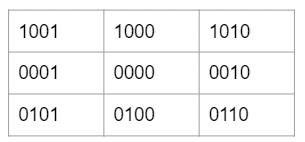
以下の表の場合、矩形に対して「上下右左」でビットが割り当てられています。「0000」が矩形に相当します。
ある点が矩形より上に位置するならば左端のビットが１になります。
ある点が矩形より下に位置するならば左から２番目のビットが１になります。

こういうのをアウトコードと言います。アウトコードには色々と流派があり、以下のような「下左上右」の例もあります。多分他にもあります。

そもそも上下左右の概念というものが、プログラム上では画面下がy+で上下がひっくり返ったりするので、最終的につじつまがあえば何でもいいものです。

線分は始点と終点の２つの点から構築されます。
なので始点と終点に対して各々アウトコードを求めます。

trivial accept(クリッピングするまでもなく受け入れる）

求めた始点と終点のアウトコードに対してブール演算のorをとります。
結果が0ならば、線分の始点と終点は完全に矩形の内側に収まります。
これは両端点共にアウトコード「0000」であるということです。それ以外にor演算で0になる組み合わせはありません。
この場合矩形による線分のちょん切り、すなわちクリッピング処理は必要ありません。線分はそのまま返ります。

クリッピングするまでもなく受け入れるケース（両端点ともに矩形内）

trivial reject（クリッピングするまでもなく拒否する）

求めた始点と終点のアウトコードに対してブール演算のandをとります。
結果が0でないならば、線分の始点と終点は完全に矩形の外側です。
結果はなにも帰りません。線分は消えます。
これは両端点ともに矩形より上領域。両端点共に矩形より下領域。両端点ともに矩形より右領域。両端点共に矩形より左領域。で、あるということを意味します。

中央の矩形をまたぐケース、すなわちクリッピングが必要なケースにおいて、両端点アウトコードのand演算は0より大きな数字、少なくとも１つのビットが立った数を返します。
中央の矩形をまたぐかもしれないケースも0より大きな数字を返します。このあたりは指でなぞった方が理解が早いです。

クリッピングするまでもなく拒否できるケース（両端点ともに左領域）

クリッピングするまでもなく拒否できるケース（両端点ともに上領域）

真面目に考えるケース

クリッピングしなければいけないかもしれないし、しなくてもいいかもしれないケース。

wikipediaに書いてあるアウトコードの生成関数を見ましょう。

OutCode ComputeOutCode(double x, double y)
{
	OutCode code;

	code = INSIDE;          // initialised as being inside of [[clip window]]

	if (x < xmin)           // to the left of clip window
		code |= LEFT;
	else if (x > xmax)      // to the right of clip window
		code |= RIGHT;
	if (y < ymin)           // below the clip window
		code |= BOTTOM;
	else if (y > ymax)      // above the clip window
		code |= TOP;

	return code;
}

比較演算子が以上や以下を使ってないことに注意します。これはつまり９つに分けた領域の境界上の扱いをどうするかの話です。

中央のクリッピング矩形の境界は線を踏んだら矩形内であると判定されることが分かります。

クリッピングの考え方は以下のようなものです。

自明なケースを除外した場合、線分の端点の少なくとも一方は矩形の外にあります。なのでアウトコード「0000」でない端点を取得します。

左領域にある端点は、矩形の左辺を伸ばした直線との交点に移動させます。
クリッピングすべきケースでは端点は矩形の左辺上に移動し、矩形の境界上は矩形内、アウトコード「0000」であると認識できます。この端点は次回のループで外せます。
クリッピングしなくてよいケースでは、端点は下領域に移動し、次回のループでは両端点ともに下領域であることから関数自体が終了します。

下領域にある端点は矩形の下辺を伸ばした直線との交点に移動させます。

１回では終わらないケース。
左領域にある端点は、最初のループで上領域に移動し、次のループで矩形の境界上に移動し、アウトコード「0000」となります。
ただし端点の判定処理を上領域から始めている場合、最初のループで矩形の境界上に移動します。

最後に、wikipediaのソースコードをコピペします。