
放射化学① ~語呂合わせで覚える放射性同位元素~
それでは今回は、「放射性同位元素」について詳しく見ていきたいと思います。
❶ 元素と周期表
数ある元素をそれぞれの化学的性質に基づいて縦と横の列に並べた表を周期表と呼びます。

[図1]に示すのは原子番号1の水素(H)から原子番号111のレントゲニウム(Rg)までの元素を記した周期表になります。縦の列を族、横の列を周期と呼び、特に同じ族にある元素どうし(つまり、周期表上で同じ縦列にある元素どうし)は類似した化学的性質を持つことで知られています。
この周期表、「水兵リーベ僕の船…」「スコッチバクローマン鉄のコルトに…」などの語呂合わせで覚えた方々も多いのではないでしょうか。確かにこの覚え方で原子番号36のクリプトン(Kr)まで覚えることはできそうですが、それ以降の原子番号の元素では手詰まりになりがちです(経験談ですが、高校時代僕もこの覚え方ではクリプトンまでしか覚えられませんでした笑)。
そこでオススメしたいのが、次のような語呂合わせになります。先ほどの「水兵リーベ…」の語呂合わせに加えて族、つまり周期表の縦の列の語呂合わせで覚えるのですね。ややお下品な表現は出てきますが、そこはどうか目を瞑っていただけると幸いです(汗)
まず、水素(H)から原子番号36のクリプトン(Kr)までの語呂合わせは次のようになります。

水(H:水素)兵(He:ヘリウム)リ(Li:リチウム)ーベ(Be:ベリリウム)ぼ(B:ホウ素)く(C:炭素)の(N:窒素 + O:酸素)ふ(F:フッ素)ね(Ne:ネオン) なぁ(Na:ナトリウム)曲がる(Mg:マグネシウム + Al:アルミニウム)シ(Si:ケイ素)ップ(P:リン)ス(S:硫黄)クラー(Cl:塩素 + Ar:アルゴン)ク(K:カリウム)閣(Ca:カルシウム)下 スコッ(Sc:スカンジウム)チ(Ti:チタン)バ(V:バナジウム)クロ(Cr:クロム)ーマン(Mn:マンガン)鉄(Fe:鉄)のコルト(Co:コバルト)に(Ni:ニッケル)銅(Cu:銅)煙(Zn:亜鉛)が(Ga:ガリウム)ゲル (Ge:ゲルマニウム)明日(As:ヒ素)は千(Se:セレン)秋(Br:臭素)楽(Kr:クリプトン)
こんな感じで中学校の理科や高校の化学で習いますが、この語呂合わせに加えて次のような語呂合わせを追加で覚えるとより暗記が楽になります。
1族(アルカリ金属) : H(水素)、Li(リチウム)、Na(ナトリウム)、(K:カリウム)、Rb(ルビジウム)、Cs(セシウム)、Fr(フランシウム)
→「エッチでリッチな彼女がルビーをセシめてフランスへ」
エッチ(H:水素)でリッチ(Li:リチウム)な(Na:ナトリウム)か(K:カリウム)のじょがルビー(Rb:ルビジウム)をセシ(Cs:セシウム)めてフランス(Fr:フランシウム)へ
2族(アルカリ土類金属) : Be(ベリリウム)、Mg(マグネシウム)、Ca(カルシウム)、Sr(ストロンチウム)、Ba(バリウム)、Ra(ラジウム)
→「ベッドに潜って彼とするとバラ色」
ベッド(Be:ベリリウム)にもぐって(Mg:マグネシウム)かれ(Ca:カルシウム)とする(Sr:ストロンチウム)とバ(Ba:バリウム)ラ(Ra:ラジウム)色
3族 : Sc(スカンジウム)、Y(イットリウム)、La(ランタン)、Ac(アクチニウム)
→「好かんと言ったらアッチ行った」
すかん(Sc:スカンジウム)といった(Y:イットリウム)ら(La:ランタン)アッチ(Ac:アクチニウム)行った
4族 : Ti(チタン)、Zr(ジルコニウム)、(Hf:ハフニウム)ら(Rf:ラザホージウム)
→「縮れた腹巻き」
ち(Ti:チタン)ぢ(Zr:ジルコニウム)れたは(Hf:ハフニウム)ら(Rf:ラザホージウム)まき
5族 : V(バナジウム)、Nb(ニオブ)、Ta(タンタル)、Db(ドブニウム)
→バナナの匂いを堪能したらドブの臭い
バナナ(V:バナジウム)のにおい(Nb:ニオブ)をたん(Ta:タンタル)能したらドブ(Db:ドブニウム)の臭い
6族 : Cr(クロム)、Mo(モリブデン)、W(タングステン)、Sg(シーボーギウム)
「来るぞもうすぐWバーガー、すぐに」
→くる(Cr:クロム)ぞもう(Mo:モリブデン)すぐダブル(W:タングステン)バーガー、すぐに(Sg:シーボーギウム)
7族 : Mn(マンガン)、Tc(テクネチウム)、Re(レニウム)、Bh(ボーリウム)
「満州鉄道列車妨害」
→まん(Mn:マンガン)州てつ(Tc:テクネチウム)道れっ(Re:レニウム)車ぼう(Bh:ボーリウム)害
8族 : Fe(鉄)、Ru(ルテニウム)、Os(オスミウム)、Hs(ハッシウム)
「フェルナンデス君お墨付きハッシー君」
→フェ(Fe:鉄)ル(Ru:ルテニウム)ナンデス君おすみ(Os:オスミウム)付きハッシー(Hs:ハッシウム)君
9族 : Co(コバルト)、Rh(ロジウム)、Ir(イリジウム)、Mt(マイトネリウム)
「この老人入れ歯みたいね」
→この(Co:コバルト)ろうじん(Rh:ロジウム)いれ(Ir:イリジウム)歯みたいね(Mt:マイトネリウム)
10族 : Ni(ニッケル)、Pd(パラジウム)、Pt(白金)、Ds(ダームスタチウム)
「日本にはプードルがピッタリだー」
→にっ(Ni:ニッケル)本にはプードル(Pd:パラジウム)がピッタリ(Pt:白金)だー(ダームスタチウム)
11族 : Cu(銅)、Ag(銀)、Au(金)、Rg(レントゲニウム)
→こちらは「銅(Cu)メダル(3位)、銀(Ag)メダル(2位)、金(Au)メダル(1位)」の順に覚えて、最後にRg(レントゲニウム)を追加する、といったイメージを持つと分かりやすいでしょう。
12族 : Zn(亜鉛)、Cd(カドミウム)、Hg(水銀)
「会えんから、カードでハグ」
→あえん(Zn:亜鉛)から、カード(Cd:カード)でハグ(Hg:水銀)
13族 : B(ホウ素)、Al(アルミニウム)、Ga(ガリウム)、In(インジウム)、Tl(タリウム)
「バストはあるが、インテリ」
→バスト(B:ホウ素)はある(Al:アルミニウム)が(Ga:ガリウム)、イン(In:インジウム)テリ(Tl:タリウム)
14族 : C(炭素)、Si(ケイ素)、Ge(ゲルマニウム)、Sn(スズ)、Pb(鉛)
「くさい下痢がすんなり治った」
→く(C:炭素)さい(Si:ケイ素)げり(Ge:ゲルマニウム)がすん(Sn:スズ)なり(Pb:鉛)治った
15族 : N(窒素)、P(リン)、As(ヒ素)、Sb(アンチモン)、Bi(ビスマス)
「チリは明日、アンチョビー大量」
→チ(N:窒素)リ(P:リン)はあす(As:ヒ素)、アンチ(Sb:アンチモン)ョビー(Bi:ビスマス)大量
(余談ですが、アンチョビーとはチリ北部海域の漁場で漁獲されており、冷凍品や塩漬品などの形で輸出されています。高校で地理選択だった方々はご存知かと思います。)
16族 : O(酸素)、S(硫黄)、Se(セレン)、Te(テルル)、Po(ポロニウム)
「オッサンが選定したポスター」
→オッ(O:酸素)サン(S:硫黄)がせん(Se:セレン)てい(Te:テルル)したポ(Po:ポロニウム)スター
17族(ハロゲン元素) : F(フッ素)、Cl(塩素)、Br(臭素)、I(ヨウ素)、At(アスタチン)
「ふっくらブラジャー愛の跡」
→ふっ(F:フッ素)くら(Cl:塩素)ブラ(Br:臭素)ジャーあい(I:ヨウ素)のあと(At:アスタチン)
18族(貴ガス元素) : He(ヘリウム)、Ne(ネオン)、Ar(アルゴン)、Kr(クリプトン)、Xe(キセノン)、Rn(ラドン)
「変な姉ちゃんある暗闇でキス連発」
→へん(He:ヘリウム)なねえ(Ne:ネオン)ちゃんある(Ar:アルゴン)くら(Kr:クリプトン)闇でキス(Xe:キセノン)れん(Rn:ラドン)発
また、La(ランタン)とAc(アクチニウム)にはさらにそれぞれ14種類の同族元素が存在します。
・ランタノイド元素 : La(ランタン)、Ce(セリウム)、Pr(プラセオジム)、Nd(ネオジム)、Pm(プロメチウム)、Sm(サマリウム)、Eu(ユーロピウム)、Gd(ガドリニウム)、Tb(テルビウム)、Dy(ジスニウム)、Ho(ホルミウム)、Er(エルビウム)、Tm(ツリウム)、Yb(イッテルビウム)、Lu(ルテシウム)
「ランドセルはプラスチック粘土 午後のサマーはヨーロッパの神様が波照間で自炊するまでホエール釣りに行ってるってよ」
→ラン( La:ランタン)ドセル(Ce:セリウム)はプラ(Pr:プラセオジム)スチックねんど(Nd:ネオジム) 午後(Pm:プロメチウム)のサマー(Sm:サマリウム)はヨーロッパ(Eu:ユーロピウム)の神さま(Gd:ガドリニウム)がはてる(Tb:テルビウム)までじすい(Dy:ジスニウム)するまでホ(Ho:ホルミウム)エール(Er:エルビウム)釣り(Tm:ツリウム)に行って(Yb:イッテルビウム)るって(Lu:ルテシウム)よ
・アクチノイド元素 : Ac(アクチニウム)、Th(トリウム)、Pa(プロトアクチニウム)、U(ウラン)、Np(ネプツニウム)、Pu(プルトニウム)、Am(アメリシウム)、Cm(キュリウム)、Bk(バークリウム)、Cf(カリホルニウム)、Es(アインスタイニウム)、Fm(フェルミウム)、Md(メンデレビウム)、No(ノーベリウム)、Lr (ローレンシウム)
「アク取りのプロが裏で眠るプールでアメリカ産キュウリをバクっと刈り取る アインシュタインはFM聴きながら麺が伸びてるだろー」
→アク(Ac:アクチニウム)とり(Th:トリウム)のプロ(Pa:プロトアクチニウム)、がウラ(U:ウラン)でねむ(Np:ネプツニウム)るプール(Pu:プルトニウム)でアメリカ(Am:アメリシウム)産キュウリ(Cm:キュリウム)をバク(Bk:バークリウム)っとかり(Cf:カリホルニウム)取る アインシュタイン(Es:アインスタイニウム)はFM(Fm:フェルミウム)聴きながら麺(Md:メンデレビウム)がのび(No:ノーベリウム)てるだろー(Lr:ローレンシウム)
特にU:ウラン(=原子番号92)より原子番号の大きいNp:ネプツニウム以降の元素は超ウラン元素と呼ばれます。
これらが原子番号1~111の元素となりますが、これらの元素は周期表上の同じ縦の列の元素どうし、つまり同族元素では互いに類似した化学的性質を持つことが知られています。
例えば同じアルカリ土類金属どうしであるCa:カルシウム、Sr:ストロンチウム、Ra:ラジウムはいずれもヒトの骨に集積する傾向があります。これはヒトの骨の主成分がリン酸カルシウム(Ca3(PO4)2)であるために、Caに類似した化学的性質を持つSrやRaまでヒトの骨に集積してしまうのです(なおヒトの骨の主成分にP:リンが含まれていることから、リンの同位体もヒトの骨に集積する傾向があります)。
他にも同じ12族元素どうしであるCd:カドミウムとHg:はいずれもヒトの生体に有毒な元素として有名です。Cdはかつて昭和の時代に富山県で蔓延したイタイイタイ病の原因であり、Hgは熊本県で蔓延した水俣病の原因ですね。
また、金属元素で重要な性質にイオン化傾向の大小関係があります。
(※)イオン化傾向
イオン化傾向とは金属元素を溶媒(水など)に溶かしたとき、その元素が陽イオンに変化する(=酸化される)度合を指します。一般的に金属元素のイオン化傾向の大小関係は次のようになることが知られています。
Li>K>Ca>Na>Mg>Al>Zn>Fe>Ni>Sn>Pb>(H)>Cu>Hg>Ag>Pt>Au
(リッチ(Li)に貸(K)そうか(Ca)な(Na)ま(Mg)ぁ(Al)ア(Zn)テ(Fe)に(Ni)すん(Sn)な(Pb)ひ(H)ど(Cu)過ぎ(Hg)る借(Pt)金(Au))
Al:アルミニウムよりもZn:亜鉛のイオン化傾向が小さい点に注意が必要です。
例えばCu2+(銅イオン)とZn2+(亜鉛イオン)を溶かした溶液にNi(ニッケル)板を浸した場合、Znよりもイオン化傾向の大きいCuがNi板に析出します。
Cu2+ + 2e- → Cu
Ni → Ni + 2e-
このイオン化傾向を利用したのが化学電池になります。化学電池につい(´;ω;`)ウッ…てはここでお話しするとかなり長話になってしまいそうですから、こちらのサイトをはじめ他サイトを参照いただけると幸いです(´;ω;`)ウッ…
https://yama-taku.science/chemistry/battery-electrolysis/battery-and-electric-current/
❷原子番号と質量数
次に、元素の原子番号と質量数について未定ましょう。
原子番号とはその元素の化学的性質を決定する数字のことで、元素の電荷の数(価数)に等しくなります。これが変化すると異なる元素に変化することになります。一方で質量数とは、その元素の原子1個分の質量を決定する数字です。具体的には原子1個分の質量は、その元素の質量数の約1.661×10^-27倍(≌1/(6.02×10^23)倍)と見なすことが出来ます。

質量数は元素記号の左上に、原子番号(=電荷の個数)は左下にそれぞれ表記します。
そもそも原子は中心に原子核が存在し、その周囲を軌道電子が取り巻く構造をしておりどの元素でも半径約10^-10[m]程度の大きさを持ちます。このうち、原子核は1価の正電荷を持つ質量およそ1.673×10^-27[kg]の陽子と、電荷を持たない質量およそ1.675×10^-27[kg]の中性子が結合し合って形成されています。なお、陽子と中性子はいずれも1個で質量数は1と見なします。(軌道)電子1個の電荷はわずか1.602×10^-19[C]程度(=電子の素電荷)であり、質量も9.11×10^-31[kg](=陽子や中性子の約1840分の1程度)しかないため、元素の原子番号と原子番号は原子核の価数の合計と質量数の合計に等しいと見なすことができます。つまり、元素の原子番号は陽子の数に等しく、質量数は陽子数と中性子数の合計であると見なすことができるのですね。
(原子番号) = (陽子数)
(質量数) = (陽子数) + (中性子数)
このうち、原子番号が同じで質量数が異なる元素どうしを同位体(アイソトープ)と呼び、さらに放射性壊変により放射線を放出する同位体を放射性同位元素(radioisotope)と呼びます。
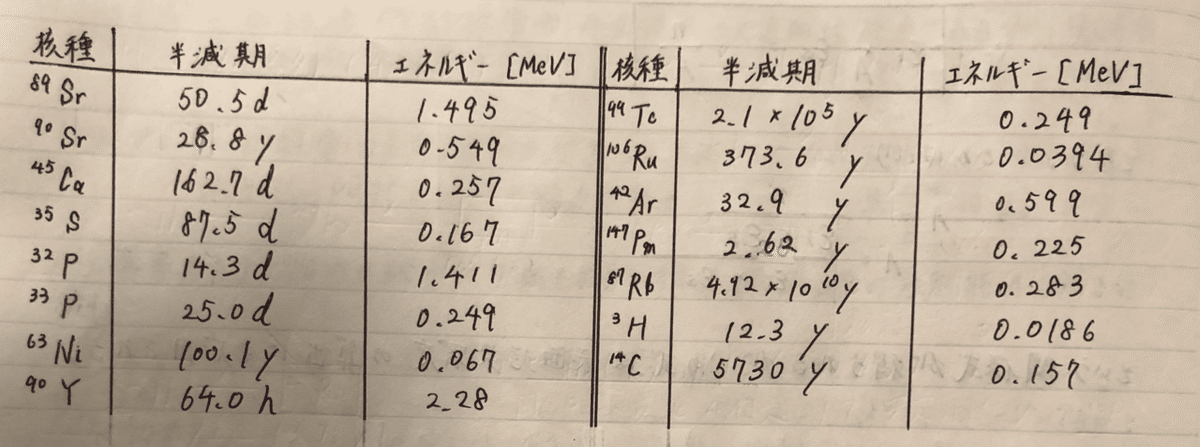

[図4-Ⅰ]と[図4-Ⅱ]にそれぞれ、純β-壊変核種の例とEC壊変(100%)の例をそれぞれ示します。β-壊変やEC壊変等の放射性壊変の種類についてはこちらの記事に詳しく書いていますので、物理学の復習がてら見直していただくと良いでしょう。
https://note.com/akira_physic/n/n994484d0f655
●純β-壊変核種 :
「するするカスピに行ってくる ある午後ハイシー」
→する(89Sr)する(90Sr)カ(45Ca)ス(35S)ピ(32P)に(63Ni)行っ(90Y)てく(99Tc)る(106Ru) ある(42Ar)午後(147Pm)ルビー(87Rb)ハイ(3H)シー(14C)
・89Sr
半減期50.5日の核種であり、1.495MeVのβ-線を放出します。
野球する(89Sr)から公園に行こ〜(1.495MeV≌1.5MeV)、ゴーゴー(半減期50.5日)
・90Sr
半減期28.8年の核種であり、0.545MeVのβ-線を放出します。β-壊変により生成した娘核種の90Yとは永続平衡(→詳細は後述)が成り立ちます。
90回する(=90Sr)とお肌艶(つや)や(半減期28.8年)か、ゴーゴー(0.545MeV≌0.55MeV)
・45Ca
半減期162.7日の核種であり、0.257MeVのβ-線を放出します。
ヒロミ(半減期162.7日≌163日)、ニコ生(0.257MeV)配信を4時5分に始めるか(45Ca)
・35S
半減期87.5日の核種であり、0.167MeVのβ-線を放出します。
やや(半減期87.5日≌88日)3コース(35S)沿いにいろな(0.167MeV)
・32P
半減期14.3日の核種であり、1.711MeVのβ-線を放出します。
イヨさん(半減期14.3日)、32ページ(32P)にいない(1.711MeV≌1.71MeV)
なおこの32Pから放出されるβ-線は、その運動エネルギーの高さからはチェレンコフ光を放出する特性が広く知られています。
※チェレンコフ光とは :

高い運動エネルギーをもつα粒子やβ-線等の荷電粒子が空気等の媒質中を通過するとき、その運動エネルギーが一定以上の大きさになると発光時間およそ3[psec]= 3×10^-12[sec]の青白い光が観測される場合があります。この青白い光をチェレンコフ光とよび、14Pや90Y等の高エネルギーβ-線放出核種の測定時に観測されます。
チェレンコフ光は電子が放出する電磁波面の接線、すなわち衝撃波面に沿って放出されます。電子の進む媒質の屈折率nに対して、媒質中の光速c_m[m・s^-1]は
c_m = c/n …(a)
で示されます。ただしcは光速(=3.0×10^8[m・s^-1])とします。一方で電子の運動エネルギーTは、電子の静止質量m=9.11×10^-31[kg]と電子の速さv[m・s^-1]に対して
T = [1/√{1-(v/c)^2} - 1]mc^2 (=(1/2)mv^2)
…(b)
で示されます。チェレンコフ光が発生するには [図5]下部の図においてc_m = vcosθ ≦ v(∵ 0°≦θ≦180°より-1≦cosθ≦1)となれば良いですから、(a)より
v ≧ c_m = c/n ∴v/c ≧ 1/n
これより√{1-(1/n)^2 ≧ √{1-(v/c)^2 ですから、
[1/√{1-(v/c)^2} ≧ [1/√{1-(1/n)^2}]
つまり(b)より、チェレンコフ光が発生するためには電子の運動エネルギーTが
T = [1/√{1-(v/c)^2} - 1]mc^2 ≧ [1/√{1-(1/n)^2} - 1]mc^2
⇔ T ≧ [1/√{1-(1/n)^2} - 1]mc^2
となれば良いのです。つまり、チェレンコフ光発生のしきいエネルギー(エネルギーの最低値)T0はT0 = [1/√{1-(1/n)^2} - 1]mc^2になるのですね。
例えば水の屈折率は1.33ですから、チェレンコフ光発生のしきいエネルギーは約0.775MeVとなります。これより、32Pや90Y等の高エネルギーβ-線放出核種は水中でチェレンコフ光を起こし得ることになります。
なおこのチェレンコフ光は液体シンチレータ等にて発生するシンチレーション光の約1/1000程度の発光減衰時間であり、応答特性に非常に優れていることからβ-線放出核種の放射能絶対測定に使用されます。
・63Ni
半減期100.1年の核種であり、0.067MeVのβ-線を放出します。
100年(半減期100.1年≌100年)労務(ろうむ)に(=63Ni)従事、おお虚(むな)(0.067MeV)しい…
・90Y
半減期64.0時間の核種であり、2.28MeVのβ-線を放出します。
虫(むし)(半減期64.0時間)取りに90回行った(90Y)らお肌にツヤ(2.28MeV)が出てきた
・99Tc
半減期21万1100年の核種であり、0.294MeVのβ-線を放出します。こちらはあまり重要な核種ではなく、むしろこの核異性体である99mTcとその親核種である99Moが重要な核種として挙げられます。
(a) 99mTc
半減期6.01時間の核種で、核異性体転移により140keVのγ線を放出します。
イシオ(140keV)さんのロト1(半減期6.01時間)等を99万回当てるテクニック(99mTc)
(b) 99Mo
半減期65.9時間のβ-壊変核種であり、β-壊変により99mTcに変化します。娘核種である99mTcとの間には過渡平衡が成立します(→後述の「○過渡平衡と永続平衡」を参照)
・106Ru
半減期373.6年の核種であり、0.0394MeVのβ-線を放出します。
mixi(ミクシー)(0.0394MeV)の登録ルー(106Ru)ル見なよ(半減期373.6年≌374年)
・42Ar
半減期32.9年の核種であり、0.599MeVのβ-線を放出します。
夜逃げしたある(42Ar)醜(みにく)(半減期32.9年)い愚(おろ)(0.599MeV≌0.6MeV)か者
・147Pm
半減期2.62年の核種であり、0.225MeVのβ-線を放出します。
午後1時47分(147Pm)は風呂に(半減期2.62年)入るには不都合(0.225MeV)だ
・87Rb
半減期492億年の核種であり、0.283MeVのβ-線を放出します。
ツバサ(0.283MeV)くんの歯並び(87Rb)は、奥歯までよく似(半減期492億年)合ってる
・3H
半減期12.3年の核種であり、0.0186MeVのβ-線を放出します。
エッチなトリオ(3H)、いつ(半減期12.3年≌12年)イく?(18.6keV≌19keV)
特にこの核種はトリチウム(三重水素)とも呼ばれ、自然界においてはHTO、つまり水分子中の水素原子が1個このトリチウムに置換された形で海水中に存在します。
自然界ではトリチウムは次のような核玉砕反応により生成されます。
14N + n(高速中性子) → 12C + 3H
つまり核玉砕反応とは、宇宙線中の高速中性子線が質量数14の窒素原子(=安定同位体)に衝突して原子核を壊し、質量数12の炭素原子(=安定同位体)とトリチウムを生成する反応ということですね。自然界ではこの核玉砕反応をはじめとしたプロセスにより年間70P(ペタ)Bq(7京Bq)程度のトリチウムが生成されます。
(※)余談ですが「京」とは「兆」の次に大きな数の単位になります。1京は1000兆の10倍ということです。また"m"などの極ありふれたSI単位や"Bq"などの放射線学でしか使用しない単位に対しては接頭辞と呼ばれる数の単位を付ける場合があります。接頭辞とは簡単に言えば「億」とか「兆」とか「京」とかいった数の単位と同じようなものですね。例えば
・p(ピコ) = 10^-12(1兆分の1)倍
・n(ナノ) = 10^-9(10億分の1)倍
・μ(マイクロ) =
・m(ミリ) =
・k(キロ) = 10^3(=1000)倍
・M(メガ) = 10^6(=100万)倍
・G(ギガ) = 10^9(=10億)倍
・T(テラ) = 10^12(=1兆)倍
といった接頭辞があります。
なお後日詳しくお話するかと思いますが、トリチウム(3H)はGM(ガイガー・ミューラー)計数管式検出器による測定ができません。通常、β-線放出核種はGM計数管式検出器により測定を行うのですが、トリチウムは放出するβ-線のエネルギーが18.6keVと他のβ-線放出核種と比べ極めて低く、このGM計数管の入射窓を透過できるだけのエネルギーを持ち合わせていないために別の検出器による測定を必要とするのです。トリチウムを測定することができる検出器は、低エネルギーβ-線放出核種や高速中性子線の測定に使用する液体シンチレーションカウンタですね。
加えて、トリチウム関連で忘れてはならない重要事項が核融合です。核融合とは比較的小さな原子核どうしが合わさって大きな原子核を生成する現象を指し、この代表例として有名なものが
2H + 3H → 4He + n
という反応です。この反応はD-T(deuterium-tritium)核融合とも呼ばれ、重水素(2H)とトリチウムの核融合反応になります。この核融合においてはおよそ17.5MeVのエネルギーを生じる発熱反応になり、うち80%にあたる14MeV程度のエネルギーが運動エネルギーとして中性子に転移します。
なお、この核融合をはじめとして発熱反応または吸熱反応における発生エネルギーの大きさ(これをQ値といいます)は反応前後の原子核の結合エネルギーにより決まります。
〇結合エネルギー
例えば上記のD-T核融合の場合、核子1個あたりの結合エネルギーは2H(重水素)で1.1MeV、3H(トリチウム)で2.9MeV、4He(ヘリウム4)で7.1MeVとなります。なお核子とは原子核を構成する要素、つまり陽子または中性子を指し、陽子と中性子が1個ずつ結合して原子核を構成する2H以上の質量数を持つ原子核で定義されます。すなわち、質量数1の水素原子核(1H原子核=プロトン)では結合エネルギーが定義されず0となります。
核子1個当たりの結合エネルギーはH~Feまで概ね原子番号の増加に伴って増大する傾向にあり、質量数60付近(Fe、Co、Niなど)で8.7MeVとなり最大値を取ります(最大になった後は徐々に結合エネルギーは減少していき、原子番号92のウランで約7.6MeV程度となります)。
※核子1個あたりの結合エネルギー
2H - 1.1MeV 10B - 6.5MeV
3H - 2.9MeV 12C - 7.68MeV
3He - 2.6MeV 14N - 7.25MeV
4He - 7.1MeV 16O - 7.98MeV
6Li - 5.3MeV 17F - 7.63MeV
7Li - 5.6MeV
なお核子1個あたりの結合エネルギーは全原子核で平均すると8.0MeV程度になりますが、これは物質の化学結合のエネルギー(=4.0eV程度)の約200万倍ものエネルギーになります。
〇結合エネルギーとQ値
さて、D-T核融合に話題を戻しますと
2H + 3H → 4He + n
という反応の前後における結合エネルギーの差は
7.1×4[MeV](4Heの結合エネルギー) - (1.1×2[MeV](2Hの結合エネルギー) + 2.9×3[MeV](3Hの結合エネルギー))
= 28.4 - (2.2 + 8.7) = 28.4 - 10.9
= 17.5 [MeV]
となります。この反応前後の結合エネルギーの差が反応のQ値に相当します。
反応のQ値
a + b + c +… → a' + b' + c' +…
という反応におけるQ値は、各々の原子核の結合エネルギーBEに対して
Q = {BE(a')+BE(b')+BE(c')…} - {BE(a)+BE(b)+BE(c)…}
・14C
半減期5730年の核種であり、0.157MeVのβ-線を放出します。
14歳の中学生(14C)はコナミ(半減期5730年)のゲーセンに行こうな(0.157MeV)
この14Cは加速器質量分析法(AMS)による考古学資料の年代測定に使用されます。
〇加速器質量分析法(AMS)
試料中の微量の放射性同位体を高感度で検出する分析法であり、14Cなどの放射性炭素の年代測定に使用されます。
例えばある試料を測定して、13C/(12C + 13C)原子数比が0.0107、14C/13C原子数比が1.75×10^-12であったとします。このときの14C/(12C + 13C)原子数比は
14C/(12C + 13C) = {13C/(12C+13C)}×(14C/13C)
= (1.07×10^-2)×(1.75×10^-12)
= 1.8725×10^-14 ≌ 1.87×10^-14 …(a)
となります。
天然の炭素中に12Cは98.9%、13Cは1.1%存在しますから、1gの炭素中に含まれる12Cと13Cの原子数の総和 : 12C + 13Cは
12C + 13C = (6.02×10^23)/(12×0.989 + 13 ×0.011)
= 5.012… × 10^22 ≌ 5.01 × 10^22[個]
となります。
一方で地球へ飛来する宇宙線の強度を一定であると仮定すれば、大気中の14Cの放射能は炭素1gあたり0.23Bqで一定となります。よって14C原子の総数 : 14Cは壊変定数λに対して
14C = 0.23/λ =0.23/(3.84×10^-12)
= 5.989… × 10^10 ≌ 5.99 × 10^10 [個]
となります。
※14Cの壊変定数λ_14Cがλ_14C = 3.84×10^-12[s^-1]と計算できる点については、後述で詳しくお話します。
よって14C/(12C + 13C)原子数比は
14C/(12C + 13C) = (5.99 × 10^10)/(5.01 × 10^22) = 1.195… × 10^-12
= 1.2 × 10^-12 …(b)
となります。(b)は時刻t=0における14C/(12C + 13C)原子数比ですから、(a)と(b)から
N(t)/N0 = exp(-λt) = (1/2) ^(t/T)
(∵ λ = ln2/Tよりexp(-λt) = exp{-(ln2/T)・t}
= [exp{(ln1/2)}]^(t/T) = (1/2)^(t/T))
= (1.87×10^-14)/(1.2×10^-12)
= 1.558…×10^-2 ≌ 1.56×10^-2 ≌ (1/64)
= (1/2)^6
よってt/T = 6 より、14Cの半減期5730年の6倍前、すなわち約3万4400年前の試料であると判断することができます。従来行われてきた液体シンチレーションカウンタによる測定法では、試料が極微量な場合や数万年前の極めて古い試料を使用する場合14Cの放射能が極めて低いため、β-線の測定による14C放射能測定および年代評価が困難であるというデメリットがあったのですが、そのデメリットを14C原子核の個数を直接カウントする小型加速器を使用することにより改善したのが前述の加速器質量分析法(AMS)という手法です。小型加速器で原子核の個数を数え上げることで上記のような14C/(12C + 13C)原子数比を算出し、そこから原子数の減少割合を求め試料の年代を評価するのですね。この手法では極微量の試料でも測定可能なうえ、数万年前の古い試料でも年代評価が可能となります。
ちなみにですが、人体中には体重の約18%の炭素が存在すると言われています。現代の放射性炭素14Cの原子数比を前述の通り
14C/(12C+13C) = 1.2×10^-12としたとき、体重50kgのヒトの体内には50×0.18=9[kg]=9000[g]の炭素が存在することになりますから、このうち14Cの質量は
9000×1.2×10^-12 = 1.08×10^-8 [g]
となります。
14Cの半減期が5730年 ≌ 1.81×10^11[s]ですから、壊変定数λ_14C[s^-1]は
λ_14C = ln2/(1.81×10^11)
0.693/(1.81×10^11) = 3.84×10^-12[s^-1]
となります。
※ 14Cの原子数比からその放射能を求めさせたり試料の年代を求めさせる問題は放射線取扱主任者試験では頻出ですので、14Cの壊変定数λ_14C = 3.84×10^-12 [s^-1]という数値は主任者試験を受験予定の方々は覚えておいた方が吉です。
14Cの原子数は{(1.08×10^-8)/14}×6.0×10^23ですから、体重50kgのヒトの体内の14Cの放射能A_14C[Bq]は
A_14C = 3.84×10^-12×{(1.08×10^-8)/14}×6.0×10^23
= 1.7773…×10^3 ≌ 1.78×10^3 [Bq]
となります。
●EC壊変(100%)核種
「ベッタリ寄せて、黒焦げマンがするバッセ、カードイン」
ベッ(7Be)タリ(201Tl)寄(123I + 125I)せ(75Se)て(55Fe)、黒(51Cr)焦(57Co)げ(68Ge)マン(54Mn)が(67Ga)する(85Sr)バッ(133
Ba)セ(139Ce)、カード(109Cd)イン(111In)
そもそもEC壊変はβ+壊変と競合する現象であり、Mp:親核の質量、Md:娘核の質量、m_e:電子の(静止)質量 のそれぞれに対して
β+壊変を起こす ⇒ Mp - Md - 2m_e > 0
Mp - Md > 0 ⇒ EC壊変を起こす
となります。これより、100%EC壊変を起こす核種はいずれも、親核-娘核の質量差が電子の静止質量の2倍以下の核種であることがわかります。
(※) β+壊変を起こすための必要条件がMp - Md - 2m_e > 0であるのは、電子-陽電子の対(ポジトロニウム)の静止質量が2m_eであることに起因します。
・7Be
半減期53.2日の核種であり、0.478MeVのγ線を放出します。
しなや(0.478MeV)かにセブンの弁(7Be)当ゴミに(半減期53.2日)出す)
・201Tl
半減期72.9時間の核種であり、0.0703MeVのγ線を放出します。
納豆(70.3keV≌70keV)なみ(半減期72.9時間≌73時間)なみにおいたる(201Tl)
・123I
半減期13.2時間の核種であり、0.159MeVのγ線を放出します。
いみじ(半減期13.2時間)くも12時3分よ(123I)り一刻(0.159MeV)
・125I
半減期59.4日の核種であり、0.0274MeVのγ線を放出します。
12時5分よ(125I)りニーナ氏(27.4keV)は獄死(半減期59.4日)
・75Se
半減期119.8日の核種であり、0.136MeVと0.265MeVのγ線を放出します。
ヒムロ(0.136MeV)とツム子(0.265MeV)には必要(半減期119.8日≌120日)性ないっ(75Se)
・55Fe
半減期2.73日の核種になります。
こ、コーヒー(55Fe)になみ(2.73日)なみとガムシロップを
・51Cr
半減期27.7日の核種であり、0.320MeVのγ線を放出します。
双葉(ふたば)(半減期27.7日≌28日)さん、恋(こい)するクリス(51Cr)にお財布を(0.320MeV)渡す
・57Co
半減期271.7日の核種であり、0.122MeVのγ線を放出します。
フナツ(半減期271.7日≌272日)とココナ(57Co)は五つ(いつつ)(0.122MeV)学年が違う
・68Ge
半減期270.9日の核種となります。
ゲルマン人は牢屋(ろうや)(68Ge)にない(半減期270.9日≌271日)
・54Mn
半減期312日の核種であり、0.835MeVのγ線を放出します。
ミューツー(半減期312日)の玄孫(やしゃご)(0.835MeV)はマンゴーよ(54Mn)
・67Ga
半減期3.26日の核種であり、0.093MeV、0.185MeV、0.300MeVのγ線を放出します。
虚(むな)しいが(67Ga)、一箱(ひとはこ)(0.185MeV)300円(0.300MeV)のリンゴが3日(半減期3.26日≌ 3日)でたくさん(0.093MeV)売れた
・85Sr
半減期64.9時間の核種であり、0.514MeVのγ線を放出します。
虫食(むしく)(半減期64.9時間)いの白箱(しろはこ)(85Sr)に小石(0.514MeV)を入れる
・133Ba
半減期10.5日の核種であり、0.356MeVのγ線を放出します。
ヒトミさんのバ(133Ba)イト(半減期10.5日≌11日)先にミズゴロウ(0.356MeV)がいる
・139Ce
半減期137.6日の核種であり、0.166MeVのγ線を放出します。
イシオ(半減期137.6日≌140日)さん、マイナ(0.166MeV ≌ 0.17MeV)スになったら意味ないぜ(139Ce)
・109Cd
半減期461.4日の核種であり、0.088MeVのγ線を放出します。
遠くの角(109Cd)の鎧(よろい)(半減期461.4日≌ 461日)の幅(88keV)
・111In
半減期2.8日の核種であり、0.171MeVのγ線を放出します。
秘密(ひみつ)の部屋にイン(111In)したら3日後(半減期2.8日≌3日)にはいない(0.171MeV)
● β+壊変とEC壊変を両方とも起こし得る核種

β+壊変とEC壊変が競合する核種には
11C、13N、15O、18F、22Na、26Al、30P、57Ni、64Cu、65Zn、67Ga
といった核種が挙げられます。中でも11C、13NO、15O、18Fといった短半減期核種はその有効半減期も短くなることから、医療においてはPET用製剤として使用されるポジトロン放出核種として有名です。
クノッフなあるプレイスにドアが
(ク(11C)ノ(13N + 15O)ッフ(18F)な(22Na
)ある(26Al)プレイス(30P)に(57Ni)ド(64Cu)ア(65Zn)が(68Ga))
・11C
半減期20分
→ いい炭素(11C)は20分(半減期20分)ででき上がる
・13N
半減期10分
→意味ない(13N)10分間(半減期10分)
・15O
半減期2分
→甥っ子(15O)2分(半減期2分)で到着
・18F
半減期110分
→18階(18F)まで上がるイトウ(半減期110分)さん
・22Na
半減期2.6年
→普通な(22Na)風呂(半減期2.6年)
・26Al
半減期71.7万年
→ある風呂(26Al)は72万年(半減期71.7万年 ≌ 72万年)前からある
・30P
半減期2.5分
→30歳でリッチ(30P)な富豪(半減期2.5分)になる
・57Ni
半減期35.6時間
→いつ何(57Ni)が見ごろ(半減期35.6時間)?
・64Cu
半減期12.7時間
→虫博士のド(64Cu)イさん(半減期12.7時間 ≌ 13時間)
・65Zn
半減期244日
→6時5分に会えん(65Zn)かな、ニシジ(半減期244日)マさん
・68Ga
半減期67.7分
→牢屋(ろうや)(半減期67.7分 ≌ 68分)にロバが(68Ga)いる
※ 有効半減期について
半減期には
① 放射性壊変により原子数が半減するのにかかる時間である物理学的半減期 : T_p
② ヒトなどの生物の体内に摂取された放射性核種が、代謝や排泄等の生理的作用により半減するのにかかる時間である生物学的半減期 : T_b
の2つがあります。一般的に知られている「半減期」とは」①の物理学的半減期ですが、放射性核種の経口摂取や吸入摂取による内部被ばくを考える際は、この物理学的半減期に加えて生物学的半減期まで考慮した体内での事実上の半減期である有効半減期 : T_eを用いて被ばくの影響を評価します。
T_e = (T_p×T_b)/(T_p + T_b)…(*)
有効半減期T_eの式は上の(*)式のようになりますが、なぜこのような式で有効半減期を求めることができるのでしょうか。
まず、物理学的半減期に起因する放射性同位元素の壊変定数をλ_p、生物学的半減期に起因する壊変定数をλ_b、有効半減期に起因する壊変定数をλ_eとします。このとき、体内に摂取する前の放射性同位元素の時刻tにおける原子数をN_p(t)、N(0)=N0とすると、
N_p(t) = N0・exp(-λ_p・t) …(**)
という指数関数によりN_P(t)は表現されます(詳細は後述の「❸放射能」を参照されてください)。
一方でこの放射性同位元素を実際に体内に摂取した場合において、体内に摂取された後の放射性同位元素の原子数N_b(t)は
N_b(t) = {N_p(t)}・exp(-λ_b・t) …(***)
となります。(**)と(***)より、
N_b(t) = {N0・exp(-λ_p・t)}・exp(-λ_b・t) = N0・exp{-(λ_p + λ_b)t}
= N0exp(-λ_e・t) …(*4)
と表すことができますから、
λ _e = λ_p + λ_b …(*4)'
となります。なお(*4)式は最初にお話ししました「物理学的半減期に加えて生物学的半減期まで考慮した体内での事実上の半減期」であるという有効半減期の定義を式で表現したものになります。
壊変定数λと半減期Tに対しては
λ = ln2/T (ln2 ≅ 0.693であり、これは2の自然対数を表します)
が成り立ちますから、(*4)'式より
ln2/T_e = ln2/T_p + ln2/T_b
⇔ 1/T_e = 1/T_p + 1/T_b
⇔ T_e = 1/(1/T_p + 1/T_b)
すなわち
T_e = (T_p×T_b)/(T_p + T_b)
となり(*)式は示されるのです。
ちなみに(*)式から、
T_e = (T_p×T_b)/(T_p + T_b) = T_b/{1 + (T_b/T_p)}
かつ
T_e = T_p/{1 + (T_p/T_b)}
が成り立ちますから、
[ⅰ] T_p>>T_bのとき T_e≅T_b
[ⅱ] T_b>>T_pのとき T_e≅T_p
となります。
例えばトリチウム : 3Hの物理学的半減期T_pはT_p=12.3年と決して短くはありませんが、生物学的半減期T_bはT_b=12日程度であり、(*4)式に基づいて有効半減期T_eを計算するとT_e ≅ 11.97[日] ≅ T_bとなり、[ⅰ]に基づいてT_eは約12日と見なして差し支えないことがわかりますね。
❸放射能
さて、放射性同位元素が放射性壊変を起こすとその元素の原子数は減少する訳ですが、具体的にどのように減少していくのでしょうか。
放射性壊変を起こす前の元素を親核種、放射性壊変により生成する元素を娘核種と呼びます。なお核種とは元素と同じ意味になりますが、放射性同位元素を指すことが多い点にも注意してください。

以降、
・親核種の半減期をT1、壊変定数をλ1
・娘核種の半減期をT2、壊変定数をλ2
・時刻tにおける親核種の原子数をN1(t)、娘核種の原子数をN2(t)としてN1(0)=N10、N2(0)= N20
として、時刻tにおける親核種の放射能A1(t)と娘核種の放射能A2(t)をそれぞれ考えます。
このとき、
dN1(t)/dt = -λ1N1(t) …(a)
dN2(t)/dt = λ1N1(t) - λ2N2(t) …(b)
という2つの微分方程式が成り立ちます。
(a)より
dN1(t)/N1(t) = -λ1dt
∴ ∫dN1(t)/N1(t) = -λ1∫dt
⇔ ln{N1(t)} = -λ1・t + A (Aは積分定数)
(※) 大学以降の数学や物理学においては、logf(x)という自然対数はlnf(x)と表記されることが多々あります。またlogf(x)は10を底とする常用対数を表すことがあります。
よってN1(t) = exp(-λ1・t + A ) = Bexp(-λ1・t)
(expA=Bとした)
N1(0) = N10より、B=N10
ゆえに
N1(t) = N10exp(-λ1・t)…(a)'
(a)'を(b)に代入すると、
dN2(t)/dt = λ1N10exp(-λ1・t) - λ2N2(t)…(b)'
ここでN2(t) = f(t)exp(-λ2・t)と置くと、
((b)'の左辺) = {df(t)/dt}・exp(-λ2・t) - λ2f(t)exp(-λ2・t)
((b)'の右辺) = λ1N10exp(-λ1・t) - λ2f(t)exp(-λ2・t)
より、
{df(t)/dt}・exp(-λ2・t) = λ1N10exp(-λ1・t)
⇔ df(t)/dt = λ1N10exp{(λ2-λ1)t}
⇔ f(t) = λ1N10∫exp{(λ2-λ1)t}dt
= {λ1N10/(λ2-λ1)}exp{(λ2-λ1)t} + C
(Cは積分定数)
N2(t) = f(t)exp(-λ2・t)より、
N2(t) = [{λ1N10/(λ2-λ1)}exp{(λ2-λ1)t} + C]exp(-λ2・t)
= {λ1N10/(λ2-λ1)}exp(-λ1・t) + Cexp(-λ2・t)…(c)
N2(0) = N20 = {λ1N10/(λ2-λ1)} + C より、
C = N20 - {λ1N10/(λ2-λ1)}
一般的にN20 = 0として扱うので、
C = - {λ1/(λ2-λ1)}・N10
ゆえにこれを(c)に代入すると、
N2(t) = {λ1/(λ2-λ1)}・N20{exp(-λ1・t) - exp(-λ2・t)}…(d)
(a)'および(d)より、求める親核種の放射能A1(t)と娘核種の放射能A2(t)は
A1(t) = λ1・N1(t) = λ1N10exp(-λ1・t)
A2(t) = λ2・N2(t) = {λ1λ2N10/(λ2-λ1)}{exp(-λ1・t) - exp(-λ2・t)}
といった具合で親核種と娘核種の放射能の経時的変化を表現することができます。
親核種の放射能 A1(t) = λ1N10exp(-λ1・t)
娘核種の放射能
A2(t) = {λ1λ2N10/(λ2-λ1)}{exp(-λ1・t) - exp(-λ2・t)}
ただし、
・親核種の壊変定数をλ1
・娘核種の壊変定数をλ2
・時刻tにおける親核種の原子数をN1(t)、娘核種の原子数をN2(t)としてN1(0)=N10、N2(0)= N20
とします。
(※) 放射能A(t)と壊変定数λ
時刻tにおける放射性同位元素の放射能A(t)は、原子数N(t)と壊変定数λの積で表現されます。 A(t) = λN(t)
放射能とは端的に説明すると放射性壊変の進むスピードを表し、単位に[Bq(ベクレル)]を使用します。さらに踏み込んだ説明をすれば、微小時間dtにおいて放射性壊変を起こす原子数の微小変化分を表します。
A(t) = λN(t) = -dN(t)/dt
また壊変定数λ[s^-1]とは放射性同位元素が放射性壊変を起こす確率を表し、(全)原子数に対する放射能の比に相当します。またλは核種の半減期T[s]に対して
λ = ln2/T ≌ 0.693/T
と表現されます(ln2は2の自然対数を取ったものです)。
○ 過渡平衡と永続平衡
放射平衡時にはでは親核種の半減期T1は娘核種の半減期T2より大きくなる(T1>T2)ため、
λ1 = ln2/T1 、 λ2 = ln2/T2
より λ2 > λ1となります。このλ1とλ2(T1とT2)の差の大きさにより、親核種と娘核種が過渡平衡の状態になるか永続平衡の状態になるかが決まります。ここで過渡平衡と永続平衡について詳しく見ていきましょう。
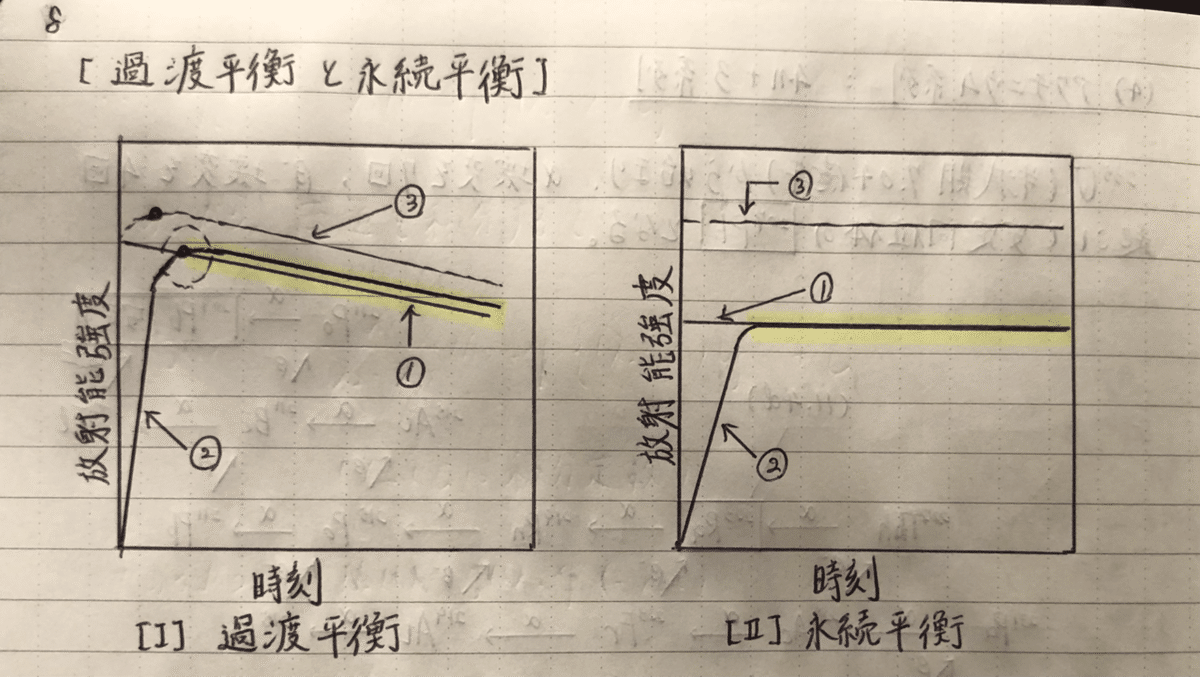
[図7]において①は親核種の放射能の、②は娘核種の放射能の経時的変化を表すグラフを示しており、その2つの合計を③に示す破線グラフのように表しています。
過渡平衡とは、放射性壊変が始まってから一定時間経過後に親核種の放射能と娘核種の放射能の比が時刻に依存せず一定となる現象を指します。一方で永続平衡とは、放射性壊変が始まってから一定時間経過後に親核種の放射能と娘核種の放射能が等しくなる現象を指します。
[ Ⅰ ] まずは親核種と娘核種の壊変定数λ1およびλ2の差が比較的大きくない場合を考えましょう。この場合、λ1とλ2の大小関係はλ2>λ1と表現されます。
N1(t) = N10exp(-λ1・t)
N2(t) = {λ1/(λ2-λ1)}・N10{exp(-λ1・t) - exp(-λ2・t)}
より、
N2(t)/N1(t) = {λ1/(λ2-λ1)}・[1 - {exp(λ1-λ2)t}]
λ1<λ2のとき、exp(λ1-λ2)t ≌ 0と見なすことができますから、
N2(t)/N1(t) ≌ λ1/(λ2-λ1)
となります。よって
A2(t)/A1(t) = {λ2N2(t)/λ1N1(t)}
≌ (λ2/λ1)・{λ1/(λ2-λ1)}
= λ2/(λ2-λ1) = (一定)
となります。つまり、親核種の放射能と娘核種の放射能の比が時刻に依存せず一定となるのですね。
[ Ⅱ ] 次に、親核種と娘核種の壊変定数λ1およびλ2の値が大きくかけ離れている場合を考えましょう。この場合、λ1とλ2の大小関係はλ2>>λ1と表現されます。
N1(t) = N10exp(-λ1・t)
N2(t) = {λ1/(λ2-λ1)}・N10{exp(-λ1・t) - exp(-λ2・t)}
より、
N2(t)/N1(t) = {λ1/(λ2-λ1)}・[1 - {exp(λ1-λ2)t}]
λ1<<λ2のとき、exp(λ1-λ2)t ≌ 0と見なすことができ、さらにλ2-λ1 ≌ λ1より
λ1/(λ2-λ1) ≌ λ1/λ2と見なすことができますから、
N2(t)/N1(t) ≌ λ1/λ2
これより
A2(t)/A1(t) = {λ2N2(t)}/{λ1N1(t)}
= (λ2λ1)・{N2(t)/N1(t)} ≌ (λ2/λ1)・(λ1/λ2)
= 1
であるから、
A1(t) = A2(t)
つまり、親核種の放射能と娘核種の放射能が等しくなるのですね。


[図6]と[図7]にそれぞれ、過渡平衡が成り立つ親核種-娘核種の組み合わせを示しています。
どのぐらい親核種と娘核種の半減期の差が離れていれば永続平衡の成り立つのかという基準は明確ではないものの、例えば
・親核種の半減期:数年程度
・娘核種の半減期:1時間程度
といったように親核種の半減期が娘核種の半減期の数千倍以上だと永続平衡が成り立ち、
・親核種の半減期:数日程度
・娘核種の半減期:数時間程度
といったように、親核種の半減期が娘核種の半減期の10倍程度~数百倍程度であれば過渡平衡が成り立つ、といったざっくりとしたイメージを持っていただけると良いのではないかと思います。
なかでも、過渡平衡が成り立つ親核種-娘核種の組み合わせとして
(a) 99Mo - 99mTc
(b) 140Ba - 140La
の2つが有名であり、また永続平衡が成り立つ親核種-娘核種の組み合わせとして
(c) 90Sr - 90Y
(d) 226Ra - 222Rn
(e) 137Cs - 137mBa
の3つが有名です。この5つの組み合わせは放射線取扱主任者試験等の試験でも頻出の重要事項ですね。
また、過渡平衡成立時の親核種と娘核種の放射能には次のような特性がある点も重要です。
① 娘核種の放射能が最大となるとき、親核種と娘核種の放射能は等しくなる。
② 親核種と娘核種の合計の放射能は、娘核種の放射能が最大となる前に最大値を取る。
① 娘核種の放射能が最大となるとき、親核種と娘核種の放射能は等しくなる。
[証明]
娘核種の放射能A2(t)は、
A2(t) = λ2N2(t)
= {(λ1λ2N10)/(λ2 - λ1)}・{exp(-λ2・t)
- exp(-λ1・t)}
であるから、
dA2(t)/dt = {(λ1λ2N10)/(λ2 - λ1)}・{λ1exp(-λ1・t)
- λ2exp(-λ2・t)}
dA2(t)/dt = 0となるとき、
λ1exp(-λ1・t) = λ2exp(-λ2・t)であるから、λ2>λ1より、
exp{(λ2-λ1)・t} = λ2/λ1
⇔ (λ2-λ1)・t = ln(λ2/λ1)
すなわち
t = {ln(λ2/λ1)}/(λ2-λ1) (∵ λ2≠λ1より)
この前後でdA2(t)/dtの符号は+→-に変化するから、A2(t)はt = {ln(λ2/λ1)}/(λ2-λ1)で極大値を取る。このときの時刻tをt=t_maxとする。
t_max = {ln(λ2/λ1)}/(λ2-λ1)…(*)
ここで
A1(t) = λ1・N1(t) = λ1N10exp(-λ1・t)
A2(t) = λ2・N2(t) = {λ1λ2N10/(λ2-λ1)}{exp(-λ1・t) - exp(-λ2・t)}
より、A1(t) = A2(t)となるとき、
λ1N10exp(-λ1・t) = {λ1λ2N10/(λ2-λ1)}{exp(-λ1・t) - exp(-λ2・t)}
⇔ exp(-λ1・t) = {λ2/(λ2-λ1)}{exp(-λ1・t) - exp(-λ2・t)}
⇔ (λ2-λ1)/λ2 = 1 - exp{(λ1-λ2)・t}
⇔ exp{(λ1-λ2)・t} = λ1/λ2
⇔ (λ1-λ2)・t = ln(λ1/λ2)
⇔ t = {ln(λ2/λ1)}/(λ2-λ1) = t_max (∵(*)より)
となり、A2(t)が最大値を取るとき、A1(t)=A2(t)となることが示される。 (証明終)
② 親核種と娘核種の合計の放射能は、娘核種の放射能が最大となる前に最大値を取る。
[証明]
A1(t) = λ1・N1(t) = λ1N10exp(-λ1・t)
A2(t) = λ2・N2(t) = {λ1λ2N10/(λ2-λ1)}{exp(-λ1・t) - exp(-λ2・t)}
より、A(t) = A1(t) + A2(t) としたとき
A(t) = λ1N10exp(-λ1・t) + {λ1λ2N10/(λ2-λ1)}{exp(-λ1・t) - exp(-λ2・t)}
= {λ1(λ2-λ1)N10/(λ2-λ1)}exp(-λ1・t) + {λ1λ2N10/(λ2-λ1)}{exp(-λ1・t) - exp(-λ2・t)}
= {λ1N10/(λ2-λ1)}・{(2λ2-λ1)exp(-λ1・t) - λ2exp(-λ2・t)}
なので、
dA(t)/dt = -(λ1^2)N10exp(-λ1・t) + {λ1λ2N10/(λ2-λ1)}{λ2exp(-λ2・t) - λ1exp(-λ1・t)}
= λ1N10[{λ2/(λ2-λ1)}{λ2exp(-λ2・t) - λ1exp(-λ1・t)} - λ1exp(-λ1・t)]
であるから、
( ⅰ ) t = 0のとき
dA(t)/dt = λ1N10[{λ2/(λ2-λ1)}(λ2 - λ1)
- λ1] = λ1N10(λ2-λ1) > 0
(∵ λ2>λ1より)
( ⅱ ) t = t_maxのとき
t_max = {ln(λ2/λ1)}/(λ2-λ1) であり、加えて
dA(t)/dt = λ1N10[{λ2/(λ2-λ1)}{λ2exp(-λ2・t) - λ1exp(-λ1・t)} - λ1exp(-λ1・t)]
= {λ1N10exp(-λ1・t)/(λ2-λ1)}([(λ2^2)exp{(λ1-λ2)t} -λ1λ2] - λ1(λ2-λ1))
= {λ1N10exp(-λ1・t)/(λ2-λ1)}([(λ2^2)exp{(λ1-λ2)t} - 2λ1λ2 + λ1^2))
より、
dA(t)/dt = {λ1N10exp(-λ1・t)/(λ2-λ1)}([(λ2^2)exp{-ln(λ2/λ1)} - 2λ1λ2 + λ1^2))
= {λ1N10exp(-λ1・t_max)/(λ2-λ1)}{(λ2^2)・(λ1/λ2) - 2λ1λ2 + λ1^2}
= {λ1N10exp(-λ1・t_max)/(λ2-λ1)}(λ1λ2 - 2λ1λ2 + λ1^2)
= {λ1N10exp(-λ1・t_max)/(λ2-λ1)}(λ1^2 - λ1λ2)
= {λ1N10exp(-λ1・t_max)/(λ2-λ1)}・λ1(λ1 - λ2)<0
(∵ λ1<λ2より)
( ⅰ )と( ⅱ )より、0<t<t_maxの範囲内でdA(t)/dtは+→-と符号変化が起こるから、A(t)はこの範囲内で極大値を取る。つまり、親核種と娘核種の合計の放射能は0<t<t_maxの範囲内で最大値を取るから、娘核種の放射能が最大となる前に親核種と娘核種の合計の放射能は最大となることが示される。 (証明終)
❹ 壊変系列を作る天然放射性核種
では最後に、4つある天然放射性核種の壊変系列について見ていきましょう。
地球が誕生したのは今から約46億年前であり、この当時から地球上に存在していた放射性核種のうち、129I(半減期1.57×10^7年)や237Np(半減期2.14×10^6年)といった地球年齢よりも短半減期の核種は減衰してしまい現在は存在しません現在も地球上に存在する放射性核種は238U(半減期4.47×10^9年)や232Th(半減期1.4×10^10年)といった長寿命の核種だけであり、これらは天然放射性核種として残って
・壊変系列を作るもの
・壊変系列を作らず、単独で存在するもの
の二つに分かれます。これらは一次放射性核種と呼ばれ、それらが壊変することで天然中に存在する核種を二次放射性核種と呼びます。また、宇宙線(=宇宙空間から放出される高速中性子線や陽子線などの放射線)や天然放射性核種などからの放射線により絶えず生成される核種を誘導放射性核種と呼びます。
原子番号81以上(つまり、Tl以降)の元素はいずれも天然放射性核種を持ちます。特に、原子番号83以上(Bi以降)の元素は安定同位体を持たず全て放射性核種となります。
※単核種元素
天然に存在する核種がただ1つのみである元素を指します。すなわち、それらは安定同位体を意味します。
9Be、19F、23Na、27Al、31P、45Sc、55Mn、59Co、75As、93Nb、89Y、103Rh、127I、133Cs、197Au、209Bi
(別(9Be)荘風(19F)な(23Na)ある(27Al)プレイス(30P) すごく(45Sc)真(55Mn)面目なこ(59Co)ひ(75As)(恋)に(93Nb)落ち、一途(89Y)に浪(103Rh)人愛(127I)せよ乙女(197Au)美(209Bi)人)
(a) 質量数が1減ると放射性核種となるもの
19F ⇔ 18F(EC+β+) : 半減期110分
23Na ⇔ 22Na(EC+β+) : 半減期2.6年
27Al ⇔ 26Al(EC+β+) : 半減期71.7万年
55Mn ⇔ 54Mn(EC100%) : 半減期312日、0.835MeVγ線を放出
(b) (n,γ)反応により放射性核種に変化するもの
23Na(n,γ)24Na → 24Na : 半減期14.96時間
31P(n,γ)32P → 32P : 半減期14.3日
59Co(n,γ)60Co → 60Co : 半減期5.27日
127I(n,γ)128I → 128I : 半減期25分
197Au(n,γ)198Au → 198Au : 半減期2.7日
(c) β-壊変またはEC壊変により生成するもの
45Sc : 45Ca(半減期162.7日、0.257MeVβ-線放出) → 45Sc
75As : 75Se(半減期119.8日、0.136MeV + 0.265MeVγ線放出) → 75As
89Y : 89Sr(半減期50.5日、1.495MeVβ-線放出)
133Cs : 133Ba(半減期10.5日、0.365MeVγ線放出) → 133Cs
なお209Biはα壊変核種ではあるのですが、半減期が2.01×10^19[年](=2010京年)と極めて長いことから安定同位体として扱われる場合もあります。
では具体的に、4つの壊変系列について見ていきましょう。天然放射性核種の壊変系列には
⑴ トリウム系列(4n系列)
⑵ ネプツニウム系列(4N+1系列)
⑶ ウラン系列(4n+2系列)
⑷ アクチニウム系列(4n+3系列)
の4つがあります。

⑴ トリウム系列(4n系列)
トリウム系列はα壊変核種の232Th(半減期1.4×10^10年=140億年)から始まり6回のα壊変と4回のβ-壊変を起こして208Pb(安定同位体)で終わる壊変系列です。系列内の核種はいずれも自然数nに対して質量数が4nとなります。
※232Th~208Pbの間では質量数が24減っており、α壊変を1回起こせば質量数が4減ってβ-壊変では質量数は変化しませんから、α壊変が6回起こることがわかります。一方でこの間に原子番号は4減っており、α壊変を4回起こせば原子番号は2×4=8だけ減ってβ-壊変を1回起こせば原子番号は1増えますから、β-壊変は8-4=4回起こるということがわかるのですね。
この壊変系列で特に重要な核種は次の2つになります。
・208Tl : 2.6MeV付近にエネルギーピークをもつγ線放出核種であり、環境中に存在するγ線放出核種としては最大エネルギーのγ線を放出します。
・220Rn : 半減期55.6秒のα壊変核種で、トロンとも呼ばれます。このトロンは222Rnと同様に環境中に存在する気体であり、自然放射線被ばくの原因となります。
⑵ ネプツニウム系列(4n+1系列)
ネプツニウム系列はα壊変核種の237Np(半減期2.14×10^6年=214万年)から始まり8回のα壊変と4回のβ-壊変を起こして205Tl(安定同位体)で終わる壊変系列です。系列内の核種はいずれも自然数nに対して質量数が4n+1となります。
※237Np~205Tlの間では質量数が32減っており、⑴の※と同様に考えればα壊変が8回起こることがわかります。一方でこの間に原子番号は12減っており、α壊変を8回起こせば原子番号は2×8=16だけ減ってβ-壊変を1回起こせば原子番号は1増えますから、β-壊変は16-12=4回起こるということがわかるのですね。
この壊変系列が他の3つの壊変系列と大きく異なるのは、最終壊変生成物である安定同位体がPb(鉛)ではなくTl(タリウム)であるということですね。なお、237Npは地球年齢46億年と比べて半減期が非常に短いことから、現在は存在しない死滅放射性核種として知られています。

⑶ ウラン系列(4n+2系列)
ウラン系列はα壊変核種の238U(半減期4.47×10^10年=44.7億年)から始まり8回のα壊変と6回のβ-壊変を起こして206Pb(安定同位体)で終わる壊変系列です。系列内の核種はいずれも自然数nに対して質量数が4n+2となります。
※238U~206Pbの間では質量数が32減っており、⑴の※と同様に考えればα壊変が8回起こることがわかります。一方でこの間に原子番号は10減っており、α壊変を8回起こせば原子番号は2×8=16だけ減ってβ-壊変を1回起こせば原子番号は1増えますから、β-壊変は16-10=6回起こるということがわかるのですね。
238Uは地球年齢とほぼ等しい半減期を持っていることから、現在もなお天然中のウランのほとんどを占めておりその割合は約99.2%にも及びます。このウラン系列で特に重要な核種は次の3つになります。
・226Ra : 半減期1600年のα壊変核種であり、α壊変により222Rnに変化します。
・222Rn : 半減期3.82日のα壊変核種であり、α壊変により218Poに変化します。
→ 226Raと222Rnはその半減期の差が非常に大きいことから永続平衡が成立する核種どうしであるという点が重要です。
・214Bi : 222Rnの子孫核種であり、609keVのγ線放出核種として環境中に存在します。この214Biのγ線は原発事故由来の134Cs(=605keVと796keVにそれぞれエネルギーピークを持つγ線放出核種)にエネルギーピークが極めて近いことから、134Cs測定時の妨害因子になり得ます。これらの検出器外部からの測定妨害因子の影響を低減するには、鉛や鉄などで検出器を取り囲み遮蔽する必要があります。
※134Cs : 605keVと796keVのカスケードγ線(=Ge半導体検出器の分解時間内に入ってくる複数のγ線)を放出する核種であり、Ge半導体検出器でエネルギースペクトルを測定するとこの2本のγ線のエネルギーピークによるサムピーク(=2つのピークのエネルギー和に相当するエネルギーにおけるピーク。これが観測される現象をサム効果という)が観測されます。

⑷ アクチニウム系列(4n+3系列)
アクチニウム系列はα壊変核種の235U(半減期7.04×10^8年=7.04億年)から始まり7回のα壊変と4回のβ-壊変を起こして207Pb(安定同位体)で終わる壊変系列です。系列内の核種はいずれも自然数nに対して質量数が4n+3となります。
※235U~207Pbの間では質量数が28減っており、⑴の※と同様に考えればα壊変が7回起こることがわかります。一方でこの間に原子番号は10減っており、α壊変を8回起こせば原子番号は2×7=14だけ減ってβ-壊変を1回起こせば原子番号は1増えますから、β-壊変は14-10=4回起こるということがわかるのですね。
235Uは天然中のウランの0.72%を占めており、主に原子力発電の核燃料に使用されます。原子力発電では235Uの核分裂反応を利用して熱を発生させ、タービンを回すことにより電力を発生させるのです。
※核分裂反応とは
質量の非常に大きい原子核に熱中性子を照射すると、原子核が2つに分裂して比較的大きなエネルギーを発生する場合があります。この現象を核分裂反応と呼びます。熱中性子とはエネルギーの低い中性子を指し、約0.025eV程度のエネルギーの中性子を指すことが多いです。235Uは熱中性子に対する核反応断面積が非常に大きく、これに熱中性子線を照射すると235Uは2つの原子核に分裂します。核分裂反応により生成したした2つの原子核を核分裂片(fall out)と呼びます。

上図に示すのは、235Uの核分裂片(核分裂生成物)の原子番号の変化に伴う収率の変化をグラフ化したものになります。このグラフより、235Uの核分裂反応時に生成する核分裂片は原子番号90~105および原子番号130~145の放射性核種が多い傾向があることがうかがえます。具体的には90Sr、99mTc、131I、137Cs、139Ce、140Baといった核種が核分裂生成物として生成しやすい傾向にあります。
・131I :
半減期13日のβ-壊変核種であり、β-壊変によりその89.5%は核異性体(=励起状態の原子核であり、原子核内部にエネルギーを蓄えており不安定な状態)である131mXeに変化し358keVのβ-線を放出します。この131mXe原子核は基底状態の131Xeに戻る過程で自身が蓄えていたエネルギーを365keVのγ線として放出します(=核異性体転移)。

この131Iは比較的エネルギーの高いβ-線とγ線を放出する特性があることから、医療においてγ線は核医学検査(=甲状腺シンチグラフィ)、β-線はアイソトープ内用療法による甲状腺癌の治療にそれぞれ使用されます。
・137Cs :
半減期30.1年のβ-壊変核種であり、β-壊変によりその94.4%は核異性体である137mBa(=半減期2.55分)に変化し514keVのβ-線を放出します。この137mBa原子核は基底状態の137Baに戻る過程で自身が蓄えていたエネルギーを662keVのγ線として放出します(=核異性体転移)。

235Uがこのような核分裂反応を起こしたとき、1核分裂あたり約200MeV程度の大きな熱エネルギーを発生させます。235U核燃料を濃縮することで核分裂時に熱エネルギーを効率よく発生させることができるため、原子力発電においては235Uを3~5%程度に濃縮して核分裂反応を起こします(この核燃料の濃縮度を100%に近づけることで原子爆弾の製造も可能となります。)
…と、放射性同位元素についてバババーッとお話をしていきましたが、皆さんついていけたでしょうか、、、><
式などの定理はまた別ですが、一気に元素を覚えるのは困難だと思いますから、化学については地道に時間をかけて暗記事項を覚えるしかなさそうですね。ここが物理学とまた違って面倒なところですが、一つ一つ整理して頭に入れていけるよう頑張りましょう。
それではまた次回もよろしくお願いします(`・ω・´)
