
放射線物理学①:そもそも放射線とは?
それでは本日は、「放射線とは何なのか」についてお話したいと思います。
初めに放射線について、教科書に書いてある定義をそのまま説明すると「高いエネルギーを持って空気等の媒質中を流れる粒子または電磁波の総称」と定義されます。

一般的に放射線と呼ばれるものは直接的または間接的に物質(原子)を電離・励起する電離放射線です。
なお紫外線や電磁波も分類としては「放射線」に属しますが、これらはエネルギーが低く(=波長が長く)、物質(原子)を電離・励起しません。
では電離放射線についてさらに細かく見ていきましょう。まずは総論的な内容を学習していきます。
直接電離放射線とはその放射線自体が電荷を持ち、物質を直接電離・励起するタイプの放射線を指します。α(アルファ)線や陽子線(p)、電子線、すなわちβ-(ベータマイナス)線、重イオン線がこれに当てはまります。
一方で間接電離放射線はそれ自体電荷を持たず、物質を直接電離・励起することはありません。水分子を電離(原子中にある電子を引き剥がすこと)・励起(原子にエネルギーを与えて不安定な状態にすること)してフリーラジカル、つまり水素ラジカル(H*)やヒドロキシラジカル(OH*)を生成し、それらフリーラジカルによって間接的に物質を電離・励起します。
光子、つまりX線やγ(ガンマ)線、中性子線(n)がこれに当てはまります。

ここで電離と励起、この2つの事象について補足します。電離とは、原子、つまり物質中の電子を電子軌道から引き離して自由電子にすることを指します。
一方で励起とは、原子核、つまり物質にエネルギーを与えて不安定な状態にすることを指します。とりわけ、準安定状態の原子核は励起核とも呼ばれます。
具体的な例を見てみましょう。99Mo(モリブデン99)が半減期65.4時間でβ-壊変して生成する99mTc(テクネチウム99m)は励起核であり、半減期6.01時間で核異性体転移して基底状態の99Tc(テクネチウム99)に変化し、140keVのγ線を放出します。
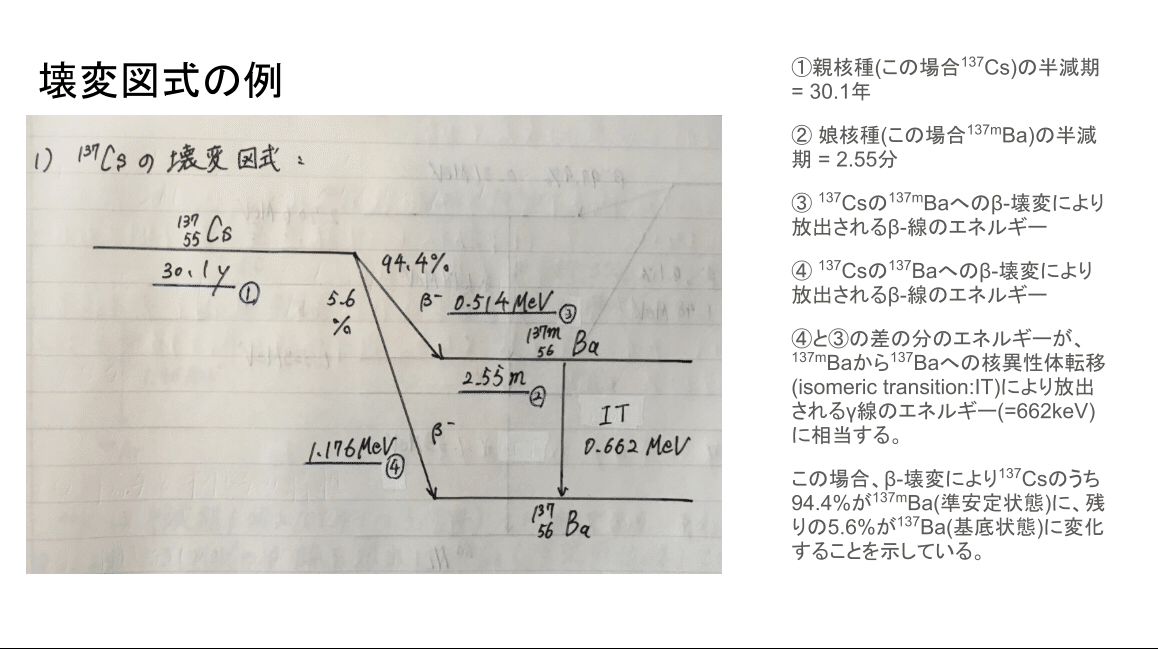
また、137Cs(セシウム137)が半減期30.1年でβ-壊変して生成する137mBa(バリウム137m)もやはり励起核であり、半減期2.50分で核異性体転移して基底状態の137Ba(バリウム137)に変化し、662keVのγ線を放出します。137Csはγ線源として知られていますが、137Csが直接γ線を放出する訳ではなくあくまで137Csがβ-壊変して生成した137mBaの核異性体転移によりγ線が放出されるという点に注意してください。

参考までに、137Csの壊変図式を示します。このような壊変図式は試験に出題されやすいため注意してください。

半減期の概念についても説明しないといけませんね。半減期とはα壊変やβ-(β+)壊変、EC壊変といった放射性壊変によって放射性同位元素の原子数と放射能が半分に減るまでにかかる時間を指します。
時刻 t における元素数がN_1(t)(N_1(0)=N_10)であり、半減期 T1 のある放射性同位元素(=親核種)が放射性壊変を起こした際 の放射能をA1(t)(A_1(0)=A_10)としたとき、その壊変定数λ1 は
λ1=(ln2)/T1
と示されます。壊変定数とは放射性同位元素が放射性壊変を起こす確率を指し、放射性同位元素の原子数に対する放射能の比で示されます。
ここでは
A_1(t) = λ1N1(t) − (*)
の関係が成り立ちます。なお ln2≌0.693 であり、自然対数の底 e=2.703...に対して e^(ln2)=2 となります。
放射性壊変によってこの放射性同位元素の放射能が減衰すると仮定したとき、
dN_1(t)/dt = -λ1N_1(t) -(**)
となります。この微分方程式を解くと
dN_1(t)/N_1(t) = -λ1・dt
すなわち
∫{dN_1(t)/N_1(t)} = -λ1∫dt
より、
ln{N1_(t)} = -λ1・t+A (Aは積分定数)
⇔N_1(t) = exp(-λ1・t+A) = Bexp(-λ1・t )
(expA=Bとした)
となります。t=0 のとき N_1(0)=N_10=B ですから、
N_1(t) = N_10exp(-λ1・t)
(なお、(*)式も用いると
exp(-ln2) = 2^-1 = 1/2より
N_1(t) = N_10・(1/2)^(t/T)
とも示されます。)
(※) exp(x)はe^xと同じ意味であり、eを底、xを指数とする指数関数を表します。
このため、時刻tにおけるこの親核種の放射能A1(t)は(*)及び(**)の2式を用いると
A_1(t) = A_10exp(−λ1・t) = λ1N_1(t) = -dN_1(t)/dt
と示されます。
この式は、放射能とは放射性同位元素の減少するスピード、すなわち放射性壊変の起こるスピードを意味することを示しているわけです。
では、各論的な内容に入りましょう。まずは直接電離放射線についてです。直接電離放射線のうち、α線について見ていきます。
① α線とは、4~6MeV程度の運動エネルギーを持つ質量数4のHe(ヘリウム)原子核、すなわちα粒子です。α壊変により原子核内部から放出されますが、α壊変は一般的に質量数200程度以上の大きめの原子核で起こりやすい傾向にあります。

質量数は原子の左上に書き、左下に原子番号(荷数)を書くというルールがあります。
陽子は質量数と荷数がいずれも1であり、中性子は質量数1で荷数ですから、
(原子番号)=(荷数)=(陽子数)
(質量数)=(陽子数)+(中性子数)
がそれぞれ成り立ちます。
ここで質量数と原子番号について少し触れておきましょう。
まず原子番号とは、元素の周期表の並びを決める数字であり、これが増減するとその元素は異なる元素に変化します。なお、周期表の縦の列は族と呼ばれ、同じ族の元素どうしは化学的に類似した性質を持ちます。

例えば2族元素(アルカリ土類金属)にはBe(ベリリウム),Mg(マグネシウム),Ca(カルシウム),Sr(ストロンチウム),Ba(バリウム),Ra(ラジウム)といった元素があります。これらの元素のうちCa(カルシウム)はヒトの体内に取り込まれると骨に集まる性質がありますが、SrやBa、Raなどの2族元素も同様にヒトの骨に集まる性質があるのです。
(※) ヒトの骨はCaPO4:リン酸カルシウムで形成されており、Ca(カルシウム)とP(リン)を取り込む性質があります。このため、45Caや32P、さらにCaと同じ2族元素の90Srや140Ba、223Raなどはヒトの体内に取り込まれると骨に集積し、内部被ばく(体内に取り込んだ放射性核種から放出される放射線による被ばく)の原因となるのです。
次に質量数とは、それぞれの元素の原子1つ分の質量(重さ)を決める数字を指します。具体的には元素の質量数に統一原子質量単位1[u]=1.66054×10^-27[kg]を掛けると、その元素の原子1個分の質量[kg]を求めることができます。
さらにいずれの元素においても、6.02×10^23個(6020垓個=6020兆個×1億)の原子が集まるとその元素の質量数と同じ質量[g]となります。これを高校化学でよく使う物質量を用いて表すと1mol(モル)となるのですね。
1mol = その元素の質量数と同じ質量[g] = 原子6.02×10^23個分の質量
さて、α粒子(=4He^2+)は2つの陽子(p)と2つの中性子(n)が合わさって形成されており、2価の正電荷を持っており6.64×10^-27[kg]程度の質量を持ちます。2価の正電荷を持っていることから遮蔽は非常に容易であり、障子の紙1枚で遮蔽することができるほどです。そのため一般的に外部被ばくのおそれはないとされています。
なおα粒子やβ-線、重イオン線のような荷電粒子には飛程が定義されます。飛程とは荷電粒子が物質(組織)内に照射されたとき、原子や電子による衝突阻止能や制動放射等の要因により元々持っていたエネルギーを全て失って停止するまでの間に荷電粒子が物質(組織)内を進む距離を表し、α粒子の場合はそのエネルギーE[MeV]に対して飛程Rα[cm]は真空中において
Rα = 0.318×E^(3/2)
と定義されます。例えば4MeVのα粒子の飛程は真空中で
Rα = 0.318×4^(3/2) = 0.318×4×2
= 1.272×2 = 2.544[cm]
となります。真空中でこれですから、地球上の空気中ではもっと短くなりますし、ヒトの組織内なら尚更です(一般的に6.8MeVのα粒子でヒトの生体組織内において40μm程度の飛程しか持ちません)。
② 次にβ-線について説明します。β-線とはざっくり言うと電子線のことで、原子核を構成する要素の1つである中性子(n)が半減期10.1分程度でβ-壊変して放出される荷電粒子を指します。
n → p + β- + ν' (但し、ν'は反ニュートリノ)
一般的にβ-壊変は、中性子過多の核種(60Coや239Uなど)で起きやすい傾向があります。
このβ-線の飛程Rβ[cm]はエネルギーの大きさにより変化しますが、遮蔽を考慮するとβ-線のエネルギーE[MeV]に対して
Rβ = 0.5×E [cm]
と定義できます。
※原子核の構成:
原子核は1価の正電荷をもつ陽子と電荷をもたない中性子の2つにより構成されます。いずれも質量数は1であり、陽子は1.673×10^-27[kg]=1.007276[u]=938.27[MeV]の質量を持ち、中性子は1.675×10^-27[kg]=1.008665[u]=939.56[MeV]の質量を持ちます。
正電荷を持つ陽子どうしではクーロン力という電荷による反発力が働くため、結合せず1つの塊を形成できません。そこで電荷を持たない中性子が介在することで、複数の陽子と中性子は1つの塊、すなわち原子核を形成できるのです。
この原子核の周りに複数の電子が配置されています。これを軌道電子といい、原子核と軌道電子を合わせて原子と呼びます。
(*)クーロン力f :
2つの荷電粒子それぞれの電荷をq_1[C]およびq_2[C]、2粒子間の距離をr[m]、(真空中の)誘電率をε_0=8.9×10^-12[C^2・N^-1・m^-2]とすると、2粒子間に働くクーロン力f[N]は
f = (1/4πε_0)・(q_1・q_2)/r^2 [N]
と示されます。
③ 次はβ+線について説明します。これはβ+壊変により放出され、陽電子とも呼ばれます。この陽電子は物質に入射すると、自身の飛程の終端付近(停止位置付近)で物質中の原子内にある軌道電子と結合した後にポジトロニウムと呼ばれる電子と陽電子の対を生成し、それが静止して消滅するときに正反対方向の2本のγ線(=消滅放射線)を放出します。
β+壊変は原子核を構成する要素の1つである陽子(p)が中性子(n)に変わってニュートリノ(ν)とβ+線を放出する現象です。
p → n + β+ + ν
ちなみにですが中性子(n)はn → p + β- + ν'というように単独で存在する場合にはβ-壊変しますが、陽子(p)は単独で存在する場合にp → n + β+ + ν という変化をしません。その理由は陽子と中性子それぞれの質量にあります。
陽子の質量は1.673×10^-27[kg] = 1.007276[u] = 938.27[MeV]、中性子の質量は1.675×10^-27[kg] = 1.008665[u] = 939.56[MeV] となるんでしたね。
一方で電子の質量は9.11×10^-31[kg]=0.000545[u]=0.511[MeV]となり、中性子の質量は陽子の質量より電子2個分以上大きくなることが分かります。このことから、n → p + β- + ν'のみ質量保存の法則を満たしているので中性子は単独でβ-壊変することが分かるわけです。
(※)[MeV]と[u]について:
① [MeV](メガエレクトロンボルト)⋯エネルギーの大きさを表す単位ですが、SI単位の[J](ジュール)とは異なる単位となります。これは主として放射線のエネルギーの単位として使用され、1[eV]の10の6乗倍(=100万倍)となりますが、1[eV]=1.602×10^-19[J]となります。電子の素電荷(=電子1個が持つ電荷)は1.602×10^-19[C]であり、それを1[V]の電位差(電圧)を印加すると電気的な位置エネルギーは1[eV]となりますが、これは1.602×10^-19[J]と同じ大きさとなります。1[eV]=1.602×10^-19[J]ということですね。一般的に放射線1本のエネルギーはジュール換算するとかなり小さいので、この[eV]という単位を使用して放射線のエネルギーの大きさを表現します。主に[keV](キロエレクトロンボルト:[eV]の1000倍)や[MeV](メガエレクトロンボルト:[eV]の100万倍)という単位で放射線のエネルギーの大きさを表現します。
なお陽子や中性子、電子や重原子核などの粒子の場合では、(静止)質量を静止エネルギーm0c^2で表現する場合もあります。cは光速度(=3.0×10^8[m・s^-1])でありm0[kg]は(相対性理論における)静止質量を表します。相対性理論においては運動する物体の質量:相対質量mは静止している質量:静止質量m0より大きくなります。この相対質量と静止質量の差は(古典力学的)運動エネルギーに相当します。
v/c<<1すなわちc>>vである場合、
(m-m0)c^2 = [1/√{1-(v/c)^2} - 1]・m0c^2
= [{1-(v/c)^2}^(-1/2) - 1]・m0c^2
≌ [1+{v^2/(2c^2)} - 1]・m0c^2
=(1/2)・m0v^2 : 古典力学的運動エネルギー
② [u](統一原子質量単位:AMU)⋯質量数12の炭素原子1個の質量の12分の1の質量を基準とした質量単位を指し、1[u]=1.66054×10^-27[kg]=931.5[MeV]となります。統一原子質量単位1[u]に原子の質量数を掛けると、その原子1個の質量に近似することができます。
β+壊変は親核種(=放射性壊変前の元素)の質量Mp、娘核種(=放射性壊変後の元素)の質量Md、電子の(静止)質量m_e(=9.11×10^-31[kg])および光速c=3.0×10^8[m・s^-1]に対して
(Mp-Md-2m_e)c^2 > 0 すなわち
Mp-Md-2m_e > 0 となるときに起こります。つまり、親核種の質量が娘核種の質量と電子2個分の質量の和より大きくなればβ+壊変が起こるわけです。
なお、Mp-Md>0となる場合はEC壊変(軌道電子捕獲)が起こります。
(※)β+壊変とEC壊変が起こる条件:
・Mp-Md-2m_e > 0 : β+壊変
・Mp-Md > 0 : EC壊変
(*)β+壊変とEC壊変は互いに競合する反応である。
EC壊変(軌道電子捕獲)とは、原子核内の陽子が軌道電子を取り込み、中性子とニュートリノ(ν)を放出する現象です。
EC壊変 : p + e- → n + ν
このEC壊変とβ+壊変は互いに競合する反応となります。また後述にも示しますが、EC壊変により軌道電子が失われることに伴って特性X線が電子軌道(=原子核の外側)から放出されます。EC壊変は核異性体転移:IT(isomeric transition)と同様γ壊変の1つとして扱われます。
核異性体転移:IT
例: 137mBa → 137Ba + γ

次は間接電離放射線について見ていきましょう。
④ まずは中性子線についてです。中性子線とはその名の通り、運動エネルギーを持った物質(空気など)中を流れる中性子を指しますが、運動エネルギーの大きさにより速中性子や熱中性子等に分類されます。
また中性子線源として代表的なものに
( ⅰ ) Am-Be線源 (ⅱ) 252Cf線源
の2つがあります。
( ⅰ ) Am-Be線源 :
α線放出核種の241Am(アメリシウム241)から放出されるα粒子を9Be(ベリリウム9)と(α,n)反応を起こすことで、速中性子線を生成・放出する線源です。
9Be + α → 12C + n : 9Be(α,n)12Cと表現します。
(※)一般的にA+a_1+a_2+…+a_n→B+b_1+b_2+…+b_nという反応は
A(a_1,a_2,…,a_n,b_1,b_2,…,b_n)
と表現します。
241Amの半減期は約433年であるため、長期にわたる使用が可能であるというメリットがありますが、中性子放出率が後述の252Cf(カリホルニウム252)の約2000分の1程度と非常に低いというデメリットもあります。
( ⅱ ) 252Cf線源 :
252Cf(カリホルニウム252)の自発核分裂(熱中性子照射を介することなく原子核が自ら核分裂反応を起こすこと)によって速中性子線が放出される性質を利用した中性子線源で、前述のAm-Be線源の2000倍の中性子放出率を持つため安定して中性子線を得ることが出来るというメリットがあります。しかし252Cfは半減期が2.62年と241Amと比べて非常に短く、長期にわたる使用が出来ないというデメリットもあります。
(※) 核分裂反応と熱中性子 :
質量数の大きな原子核に熱中性子を照射すると2つの原子核に分裂する現象を核分裂反応と呼びます。

235U(ウラン235は熱中性子に対する核反応断面積(=核反応が起こる確率)が大きく、核分裂反応を起こす際に使用される核種として代表的なものになります。一般的に235Uが熱中性子線照射により核分裂反応を起こした場合には、質量数が90~105および130~145の範囲にある核種(90Sr、99mTc、131I、137Cs、140Ba等)が核分裂生成物として放出される傾向にあり、特に質量数95および140の核種が最も多く核分裂生成物として放出されます。

235Uの中性子線に対する核分裂反応断面積は、[図Ⅸ]のように(とりわけ中性子の運動エネルギー1[eV]以下の比較的低エネルギー側で)中性子線のエネルギー増加に伴い減少していくことが分かります。
一般的に235Uの核分裂反応断面積は中性子線の運動エネルギーの平方根、つまり中性子線の速さに逆比例することが知られています。
235Uの核分裂反応断面積σ[b]は
σ∝1/√En=1/vn [b]
(ただしEnは中性子線の運動エネルギー、vnは中性子線の速さを表す)
(※)[b](バーン:barn)は面積の単位であり、
1[b]=10^-24[cm^2]=10^-28[m^2]となります。
あくまでイメージですが、熱中性子を爆弾と見立てて
(a)速いスピードで通過する中性子線→ 爆発する前に原子核を通り過ぎる
(b)遅いスピードで通過する中性子線→原子核を通り過ぎる前に爆発する(=核分裂反応を起こす)
と考えたら分かりやすいかと思います。
また中性子は核分裂反応以外にも様々な核種と(n,γ)、(n,p)等の核反応を起こします。
例:)
3He(n,p)3H 197Au(n,γ)198Au
10B(n,α)7Li 59Co(n,γ)60Co

例として、上の[図Ⅹ]のように安定元素である59Co(コバルト59)に熱中性子を照射することでβ-壊変核種の60Coが生成されます。この60Coはβ-壊変を起こして励起状態(エネルギーを蓄え不安定な状態)の60Ni(ニッケル60)原子核に変化するのですが、この励起状態の60Ni原子核は1.173MeVと1.333MeVの2本のγ線を放出して基底状態(安定元素)に変化します。
(※)このうち
⑴ 3He + n → 3H + pという反応は764keVの発熱反応になります。これは荷電粒子(=陽子:p)放出反応であり、3He比例計数管という熱中性子検出器の測定原理に使用されています。なお3Heは熱中性子に対する核反応断面積が5300[b]と気体原子の中では最も大きくなっています。
⑵ 10B + n → 7Li + αという反応は
( ⅰ ) BF3比例計数管
( ⅱ ) ホウ素中性子捕捉療法(BNCT:Boron Neutron Capturing Therapy)
に使用されます。
( ⅰ ) BF3比例計数管は荷電粒子(=α粒子)放出反応であり、熱中性子用検出器として使用されます。
( ⅱ ) ホウ素中性子捕捉療法(BNCT:Boron Neutron Capturing Therapy)はがん治療の1つであり、ホウ素を含む薬剤を生体内に投与した後に熱中性子を照射して生成するリチウム原子核(7Li^3+)とα粒子を癌細胞に照射する放射線治療です。このホウ素を含む薬剤は癌細胞に特異的に集積しますが、これに熱中性子を照射することで10B(n,α)7Li反応が起こりα粒子と7Li原子核が放出されるという訳ですね。この核反応で放出されるα粒子の飛程は5~14[μm]程度と細胞1個の大きさと同程度になります。この核反応で放出される7Li原子核はホットアトムと呼びます。
② 次にX線とγ線についてお話します。この2つはいずれも光子と呼ばれ、質量を持たない電磁放射線です。
これら光子は質量を持たないので、エネルギーは荷電粒子や中性子のようにmc^2であったり或いは(1/2)・mv^2であったりといった形で表現することが出来ません。光子のエネルギーはブランク定数h=6.63×10^-34[J・s]と自身の周波数ν[s^-1](=c/λ : λは光子の波長[m]、c=3.0×10^8[m・s^-1](光速))を掛け合わせて表現されます。
E_x,γ = hν = (hc)/λ : 光子のエネルギー
(また、E_x,γを光速cで割ると運動量という物理量を表現できます。運動量は撃力ともよび、端的に言うと物体に及ぼす衝撃の強さを表します。)
X線とγ線の大きな違いはやはり、原子核の内部で発生するか原子核の外側で発生するかということかと思います。
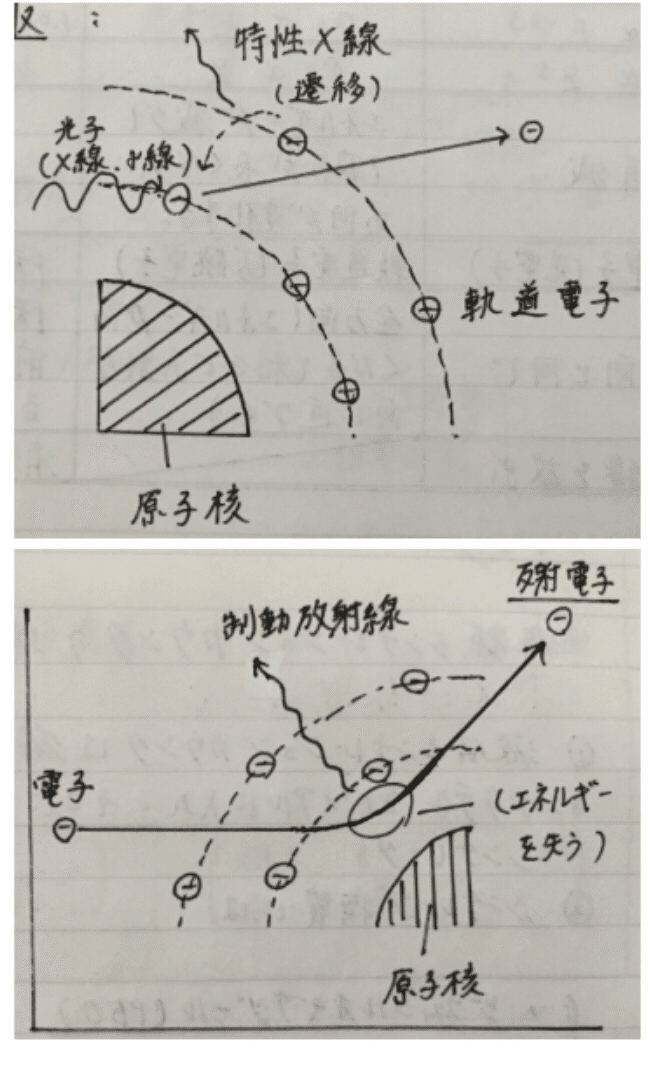
γ線は原子核内部から発生する光子ですが、X線は原子核の外側で発生する光子です。X線として有名なものは2つありまして、前述にありました特性X線と制動放射線(制動X線)の2つになります。それぞれについて詳しく見ていきましょう。
⑴ 特性X線⋯軌道電子が電子軌道から失われ空席ができると、別の殻(軌道)から軌道電子が1個空席の位置に遷移します。主に内側の殻の軌道電子が外側の殻の空席に遷移しますが、このとき遷移する前の内側の殻における原子核の束縛エネルギーと電子の運動エネルギーの和(=電離エネルギー)は遷移後の外側の殻におけるそれより大きいため、遷移前後での殻の束縛エネルギーに差が生じます。この差のエネルギーがX線として放出されますが、これを特性X線と呼ぶのです。
(※) 原子核は1価の正電荷を持つ陽子と電荷を持たない中性子がいくつも合わさってできた1つの塊であるため、それ自体は正電荷を持ちます。

一方で電子は1価の負の電荷を持ちますから、原子核と電子の間にはクーロン力(引力)が働き電子が束縛されます。
クーロン力f(R) :
原子核の価数をZとすると、
f(R)= (1/4πε0)・{(Ze^2)/R^2}
但しeは電子の素電荷でe=1.602×10^-19[C]、ε0は真空中の誘電率でε0=8.9×10^-12[C^2・N^-1・m^-2]、Rは原子核-電子間の距離とする。
このクーロン力を定点R=rから無限遠点(R=∞)まで積分すると、クーロン力による位置エネルギー、すなわちこの場合における電子の束縛エネルギーを求めることができます。
クーロン力による位置エネルギーU :
U=-∫[x,r]f(R)dR
= -∫[x,r](1/4πε_0)・{(Ze^2)/R^2}dR
= -{(Ze^2)/4πε_0}∫[x,r](1/R^2)dR
= -{(Ze^2)/4πε_0}[-1/R][x,r]
= -(Ze^2)/4πε_0}{(1/r)-(1/x)}
→-{(Ze^2)/4πε_0}・(1/r) = -(Ze^2)/4πε_0r
(x→∞のとき) …(*)
すなわち、クーロン力による位置エネルギー(=電子の束縛エネルギー)は原子核からの距離rに反比例することが分かります。

加えて電子軌道上で軌道電子は原子核の周囲を円運動しているものと見なすことができ、原子核からのクーロン力と電子に働く遠心力(=見かけ上働く力)は釣り合いますから、原子核の中心から電子までの距離rに対して
(m_e・v^2)/r = (1/4πε_0)・{(Ze^2)/r^2} …(a)
が成り立ちます。但しm_eは電子の質量(=9.11×10^-31 [kg])、vは電子軌道の接線方向における速さ[m・s^-1]とします。
また電子の運動エネルギーK=(1/2)・m_e・v^2とクーロン力による位置エネルギーUを足し合わせると電子の全エネルギーEにに等しくなりますから、(*)より
E = K + U = {(1/2)・m_e・v^2} -(Ze^2)/4πε_0r …(b)
が成り立ちます。
(a)と(b)に、ド・ブロイ波長を考慮したボーア半径r_nを考慮する(r→r_nと置き換える)ことで、原子核の最も外側(=K殻)からn(n=1,2,3…)番目における電子の全エネルギーE_nを求めることができます。
ボーア半径 : r_n = n×(h/2πm_ev) …(c)
但しhブランク定数でありh=6.63×10^-34[J・s]とします。すなわち、その全周が電子のドブロイ波長の整数倍となるような半径をボーア半径と定義します。
詳細な計算過程は割愛しますが、(a)~(c)よりE→E_nと置き換えるとK殻から数えてn番目の電子の全エネルギーE_nは
E_n = -{m_e・(Ze^2)^2}/{8・(ε_0・h)^2}・(1/n^2)
と表すことができます。水素の場合Z=1ですから、
m_e = 9.11×10^-31 [kg]:電子の静止質量
e=1.602×10^-19 [C]:電子の素電荷
ε_0 = 8.9×10^-12 [C^2・N^-2・m^-1]:真空中における誘電率
h = 6.63×10^-34 [J・s]:ブランク定数
を用いて{m_e・(Ze^2)^2}/{8・(ε_0・h)^2}を計算すると、
{m_e・(Ze^2)^2}/{8・(ε_0・h)^2} ≌ 13.6[eV]
と示されます。すなわち、E_nは水素原子の場合で
E_n = -13.6/n^2 [eV] …(d)
と簡略化できるわけですね。
このとき、n=3(=M殻)の軌道電子がn=1(K殻)に遷移した場合を考えます。このときn=3における電子の全エネルギーE_3とn=1における電子の全エネルギーE_1の差は、(d)式より
E_3 - E_1 = -13.6・(1/9 - 1)
= -13.6・(-8/9) ≌ 12.1 [eV]
となります。すなわちこれが、水素原子においてM殻からK殻に軌道電子が遷移したときに放出される特性X線のエネルギーとなります。
このようにボーアの原子模型から特性X線のエネルギーを求めさせる問題が、過去の放射線取扱主任者試験(第1種、令和4年度)に出題されています。
軌道電子が別の殻に遷移しても特性X線が放出されず、代わりにその特性X線の持つエネルギーが軌道電子に付与されて電子が殻から飛び出る場合があります。この現象をオージェ効果と呼び、このとき電子軌道外に飛び出る電子をオージェ電子と呼びます。
オージェ効果と特性X線放出は互いに競合する反応であるため、オージェ効果が起こったとき生じる電子軌道上の空席に別軌道の電子が遷移する際にさらに連続してオージェ効果が起こることも理論上は有り得るのです。
またオージェ効果に類似した現象として内部転換も是非押さえたいところですね。内部転換とは、γ線が放出されない代わりにγ線の持つエネルギーが軌道電子に付与されて電子が殻外に飛び出る現象を指します。
この内部転換に際して、γ線か放出される確率P_γに対する内部転換電子が放出される確率P_eの比を(全)内部転換係数:αと定義します。
α = P_e/P_γ…(a) : 内部転換係数
またγ壊変(EC壊変、核異性体転移等)が起こる確率をPとすると、
P = P_e + P_γ …(b)
ですから、(a)と(b)を用いると
P_γ = (P_γ/P)•P = {P_γ/(P_e + P_γ)}・P
= P/{1 + (P_e/P_γ)} = P/(1+α)
となります。
内部転換が起こると電子軌道に空席ができるため、別の軌道からが遷移して特性X線またはオージェ電子が放出されます。
⑵ 制動放射線(制動X線)・・・(自由)電子が原子核の近傍を通過するとき、電子は原子核によるクーロン力(引力)を受け進路がねじ曲げられます。このとき電子は運動エネルギーの一部を奪われますが、この奪われたエネルギーがX線として外部に放出されます。このX線を制動放射線とよび、この制動放射線が放出される現象を制動放射と呼びます。

レントゲン写真を皆さん撮ったことが一度ぐらいはあるかと思います。レントゲン撮影は正式には単純X線撮影と呼びますが、このように医療で使われるX線の正体はこの制動放射線なのです(単純X線撮影だけでなく、CT検査や透視検査(胃のバリウム検査や血管撮影等)にも制動放射線が使われます)。
最後にγ線についてお話します。


γ線は励起状態(=エネルギーを蓄えて不安定な状態)の原子核から放出される電磁放射線ですが、X線との最大の違いは原子核の内部から放出されるという特徴です。
例えば137mBa(バリウム137m)という核種は励起状態の原子核であり、[図XⅣ]および[図XⅤ]のように核異性体転移(isomeric transition : IT)を起こして662keVのγ線(=原子核内部に蓄えられていたエネルギー)を放出し、基底状態(=安定元素)の137Ba(バリウム137)に変化します。
(※)137mBaの"m"は"metastable(準安定状態)"の頭文字です。(厳密にはそうではありませんが)β-壊変を起こしてエネルギーを放出し、一見すると安定状態のように見える、というイメージを持つと分かりやすいかも知れません。
この137Cs以外にもβ-壊変により生成した核異性体(=準安定状態の核種)からγ線が放出される核種は他にもあります。代表的なものとしては60Co(コバルト60)や131I(ヨウ素131)が挙げられます。
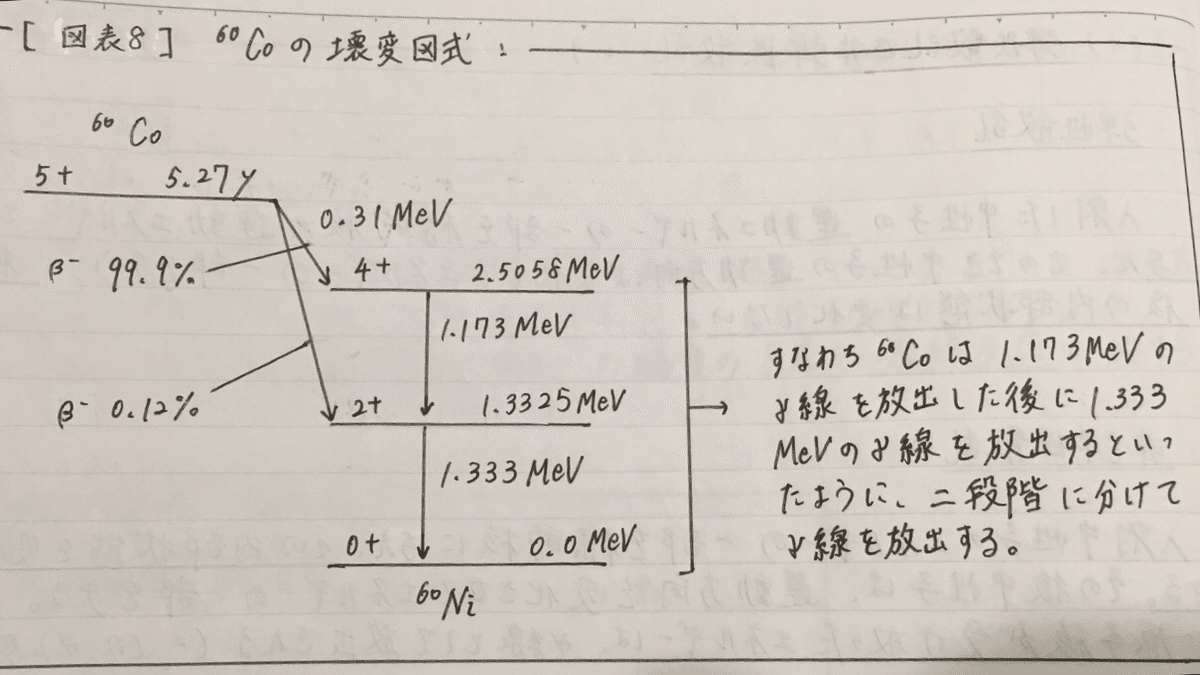
中でも60Coはカスケードγ線を放出する核種として有名ですね。
放射線を検出する機器はいくつかタイプがあるのですが、X線やγ線の検出に際してはGe(ゲルマニウム)半導体検出器が使用されます。Geの単結晶に
( ⅰ ) P(リン)やAs(ヒ素)など5価元素を加えたn型半導体
と
( ⅱ ) B(ホウ素)やAl(アルミニウム)、Ga(ガリウム)など3価元素を加えたp型半導体
を接続して、電源の陽極側をn型半導体に、陰極側をp型半導体にそれぞれ接続して逆方向の電圧を印加することでX線やγ線を検出できるようになります。

このGe半導体検出器には分解時間といって、実際に放射線が検出器に入射してから検出器が放射線を検出し始めるまでのタイムラグが発生します。この分解時間の間に新たに放射線が検出に入射してしまうと、(見かけ上)1つの核種から2種類の異なるエネルギーの放射線が放出されてしまうのです。このような現象が先ほど挙げました60Coのβ-壊変により生成した(励起状態の)60Niや134Csといった核種で見られ、これをカスケードγ線と呼ぶのです。
134Csもまた重要な核種でして、606keVと796keVの2本のカスケードγ線を放出するγ線放出核種なのですが、これは原発事故由来の核種で環境中に存在すること、そしてこの134Csの2本のγ線が別のγ線を測定する際に妨害因子となりやすいという点も重要です。
なお、環境中に存在するγ線放出核種として208Tl(タリウム208)も重要です。これは212Bi(ビスマス212)がα壊変を起こして生成する核種で、天然中に存在するγ線放出核種のγ線エネルギーとしては最大の2.6MeVのγ線を放出することで有名です。

トリウム系列とは天然放射性核種の壊変系列の1つであり、半減期140億年でα壊変する232Th(トリウム232)から始まりα壊変を6回、β-壊変を4回起こして最終的に安定元素である208Pb(鉛208)に変化する系列を指します。この壊変系列に属する核種は全て質量数が4の倍数(4n : n=1,2,3…)になります。ここでは詳細は割愛しますが、天然放射性核種の壊変系列は4つあり(トリウム系列:4n系列、ネプツニウム系列:4n+1系列、ウラン系列:4n+2系列、アクチニウム系列:4n+3)、いずれの壊変系列においても放射性核種はほとんどα壊変かβ-壊変の2種類のみの放射性壊変しかしません。
β-壊変 : n → p + ν' + β-
ここでβ-壊変の反応式を思い出してみましょう。β-壊変とは原子核内部の中性子:nが陽子:pに変化して反ニュートリノ:ν'とβ-線を放出する現象でしたね。中性子の質量数は1、価数(=原子番号)は0であり、陽子の質量数と価数はいずれも1です。つまり、β-壊変後には原子核の質量数は±0、原子番号は+1となるのです。
一方でα壊変は原子核から質量数4のヘリウム原子核(2価の正電荷を持ちます)が飛び出る現象ですから、壊変後の質量数は-4、原子番号は-2となります。
これらを鑑みると、4種類の壊変系列はいずれも全ての放射性核種で壊変の前後で質量数が4だけ増減することが分かります。すなわち4つの壊変系列それぞれにおいて核種の質量数が4n、4n+1、4n+2、4n+3と壊変前後で規則的に変化するのですね。
…と、話が横道に逸れまくりでしたが、放射線とは何なのか、概略についてお話をさせていただきました。
僕も書きながら驚いたんですが、なんとこの記事で14500文字分も放射線について語ってしまっていたみたいですね(^_^;
まだ「概略」だけで14500文字ですから、各論を説明したら…😱
次回からは出来る限りコンパクトにまとめて記事にしたいと思います笑
次回は「放射線の線量の考え方」についてお話したいと思います。では失礼します〜
