
「ChatGPTは小学生に勝てない!」って言われちゃってますが実際どうなの?検証
下記の記事で、ロジックパズルを間違えてしまう、ChatGPTに対して「小学生にも勝てない!」と言われちゃっています。
ですがさすがにこのロジックパズルは小学生には難しすぎる様な気がします。確かに、トイプロで上位10番などに入っている小学生(ロジック脳が不自由な筆者からみたら多分ギフテッドだと思う)はこのロジックパズルを解く論理思考を持っているかもしれません。
(小中学生向けpython学習サービストイプロの事は別のNoteにまとめましたので合わせてご覧ください。)
ChatGPTの名誉挽回のために同じ問題をさせてみた
まずは手始めにGPT-3.5に解かせてみたら、やはりできない。記事には間違えてE君と回答したと書いてありましたが、筆者が試してみたらDと言ってしまいました。
問題を解決するために、各発言を分析していきましょう。
Aは「ぼくもCもおならをしたのを隠している人ではありません」と言っています。したがって、AとCはおならをしたのを隠していないことがわかります。
Bは「A、C、Dの中の誰かがおならをしたのを隠している人です」と言っています。これはDがおならをしたのを隠している可能性があることを示しています。
Cは「Eはおならをしたのを隠している人ではありません」と言っています。したがって、Eはおならをしたのを隠していないことがわかります。
Dは「A、C、Eはおならをしたのを隠している人ではありません」と言っています。これはA、C、Eがおならをしたのを隠していないことを示しています。
Eは「A、Bのどちらかがおならをしたのを隠している人です」と言っています。これはAかBのどちらかがおならをしたのを隠している可能性があることを示しています。
これらの情報を組み合わせると、AとCはおならをしたのを隠していないことが確定しています。さらに、Dはおならをしたのを隠している可能性があることが示されています。
したがって、おならをしたのを隠している人はDです。

その後、「問題の正解はBです。」と種明かしをすると、この様に修正を掛けて来ました。
おっしゃる通りです。申し訳ありませんが、前回の回答に誤りがありました。
再度、各発言を分析して正解を求めましょう。
Aは「ぼくもCもおならをしたのを隠している人ではありません」と言っています。したがって、AとCはおならをしたのを隠していないことがわかります。
Bは「A、C、Dの中の誰かがおならをしたのを隠している人です」と言っています。したがって、A、C、Dのうち少なくとも一人はおならをしたのを隠していることがわかります。
Cは「Eはおならをしたのを隠している人ではありません」と言っています。したがって、Eはおならをしたのを隠していないことがわかります。
Dは「A、C、Eはおならをしたのを隠している人ではありません」と言っています。したがって、A、C、Eはおならをしたのを隠していないことがわかります。
Eは「A、Bのどちらかがおならをしたのを隠している人です」と言っています。したがって、AかBのどちらかがおならをしたのを隠している可能性があります。
これらの情報を組み合わせると、A、C、Eはおならをしたのを隠していないことが確定しています。また、Bはおならをしたのを隠している可能性があります。
したがって、おならをしたのを隠している人はBです。お答えに間違いがあり、申し訳ありませんでした。正しい回答はBです。
GPT-4に名誉挽回をしてもらった
これはpythonを使って論理的に解かせるべきと思い、GPT-4のModel: Code Interpreterに解かせてみる事にしました。
筆者問:GPT-3.5が解けない問題があるのですが、pythonを使って解く事は可能でしょうか?
そして上記記事の問題を投げたら、
GPT-4返答:
この問題は論理パズルであり、Pythonを使って解くことが可能です。それぞれの人物の主張を論理的に評価し、一致するパターンを見つけることで解答を導き出すことができます。この問題は次のように考えることができます:
すべての人物が真実を言っていると仮定します。
それぞれの主張をチェックします。主張が正しい場合、その人物は真実を言っていると考えられます。
すべての主張が真実になるようなパターンを探します。そういうパターンが見つからない場合、その人物はウソをついていると考えられます。
最終的に一人だけがウソをついているとなるパターンを探します。その人物がおならをした人物となります。
それではPythonを使ってこの問題を解いてみましょう。
といいながらも、結局、
すみませんが、コードの実行結果が表示されていません。不具合が発生した可能性があります。それでも問題が解決しない場合は、手動で各ステートメントを評価してみてください。また、このパズルの一部のステートメントは他のステートメントと競合しているため、全てのステートメントが同時に真になる組み合わせは存在しない可能性があります。その場合は、誰が嘘をついているかを判断するために追加の情報が必要となります。
と最初は匙を投げました。
種明かしをするとそれを織り交ぜたコードを書いた
筆者が「うそつきはB君です」と種明かしをすると、下記の様なコードを書きました。
# Bがウソをついている(つまり、おならをした)という前提で、他の4人(A、C、D、E)が真実を語っているかを確認します。
# 真実を語っている人(A、C、D、E)の発言が真であることを確認します。
# 各人物が真実を言っているかウソをついているかを表す真理値のリストを作成します。
# Bがウソをついていることがわかっているので、BだけFalseとします。他の人物はTrueとします。
truths = {'A': True, 'B': False, 'C': True, 'D': True, 'E': True}
# Aの発言「ぼくもCもおならをしたのを隠している人ではありません」が真であることを確認します。
assert truths['A'] == truths['C'] == True
# Cの発言「Eはおならをしたのを隠している人ではありません」が真であることを確認します。
assert truths['E'] == True
# Dの発言「A、C、Eはおならをしたのを隠している人ではありません」が真であることを確認します。
assert truths['A'] == truths['C'] == truths['E'] == True
# Eの発言「A、Bのどちらかがおならをしたのを隠している人です」が真であることを確認します。
assert truths['A'] != truths['B']
# Bの発言「A、C、Dの中の誰かがおならをしたのを隠している人です」が偽であることを確認します。
assert truths['A'] == truths['C'] == truths['D'] == True
print(truths)
しれっと、こんなコードを織り交ぜて解を出したので、
# Bがウソをついていることがわかっているので、BだけFalseとします。他の人物はTrueとします。
truths = {'A': True, 'B': False, 'C': True, 'D': True, 'E': True}筆者問:「Bがウソをついていることがわかっていない」状態で「Bがウソをついている」事を見抜くコードは書けないのですか?
と問うたところ、GPT-4は本気を出しました。
もう一度それぞれの発言を確認してみましょう
以下、GPT-4の回答です:
もう一度それぞれの発言を確認してみましょう:
A: 「ぼくもCもおならをしたのを隠している人ではありません」
B: 「A、C、Dの中の誰かがおならをしたのを隠している人です」
C: 「Eはおならをしたのを隠している人ではありません」
D: 「A、C、Eはおならをしたのを隠している人ではありません」
E: 「A、Bのどちらかがおならをしたのを隠している人です」
そして、この問題は「ウソをついている(おならをした)のは一人だけ」という条件があるため、これらのステートメントが全て真となるような解が存在するはずです。
問題の条件を満たす組み合わせを見つけるために、上記の論理式を正しく実装し直すことが必要です。それでは、コードを修正してみましょう。
from itertools import product
# 全ての組み合わせを試します
for truths in product([True, False], repeat=5):
# 各人物が真実を言っているかウソをついているかを表す真理値のリストを作成します
truths_dict = dict(zip(['A', 'B', 'C', 'D', 'E'], truths))
# 各人物の発言が真であるか確認します
# A「ぼくもCもおならをしたのを隠している人ではありません」
A_statement = (truths_dict['A'] == True) and (truths_dict['C'] == True)
# B「A、C、Dの中の誰かがおならをしたのを隠している人です」
B_statement = (truths_dict['A'] == False) or (truths_dict['C'] == False) or (truths_dict['D'] == False)
# C「Eはおならをしたのを隠している人ではありません」
C_statement = truths_dict['E'] == True
# D「A、C、Eはおならをしたのを隠している人ではありません」
D_statement = (truths_dict['A'] == True) and (truths_dict['C'] == True) and (truths_dict['E'] == True)
# E「A、Bのどちらかがおならをしたのを隠している人です」
E_statement = (truths_dict['A'] == False) or (truths_dict['B'] == False)
# 各人物が言っていることが本当になる場合の真理値
statements_truths = { 'A': A_statement, 'B': B_statement, 'C': C_statement, 'D': D_statement, 'E': E_statement }
# すべての発言が真であるか、またウソをついている(おならをした)のが一人だけであるか確認します
if all(truths_dict[person] == statements_truths[person] for person in truths_dict) and list(truths_dict.values()).count(False) == 1:
liar = [person for person in truths_dict if truths_dict[person] == False][0]
break
liar
今度は期待通りの結果が得られました。嘘つき(おならをした人)は'B'で、他の全員が真実を言っていることが確認できました。
なお、truths_dictとstatements_truthsはそれぞれ各人物がウソをついているか(Falseがウソつき、つまりおならをした人)と各人物の発言が真であるかを表しています。
したがって、このコードは「Bがウソをついていることがわかっていない」状態から「Bがウソをついている」ことを見抜くことができました。
と、ご本人もまんざらではない様子。早速Jupytorを立ち上げ検証してみるとバッチリ「B」と言う実行結果になりました。
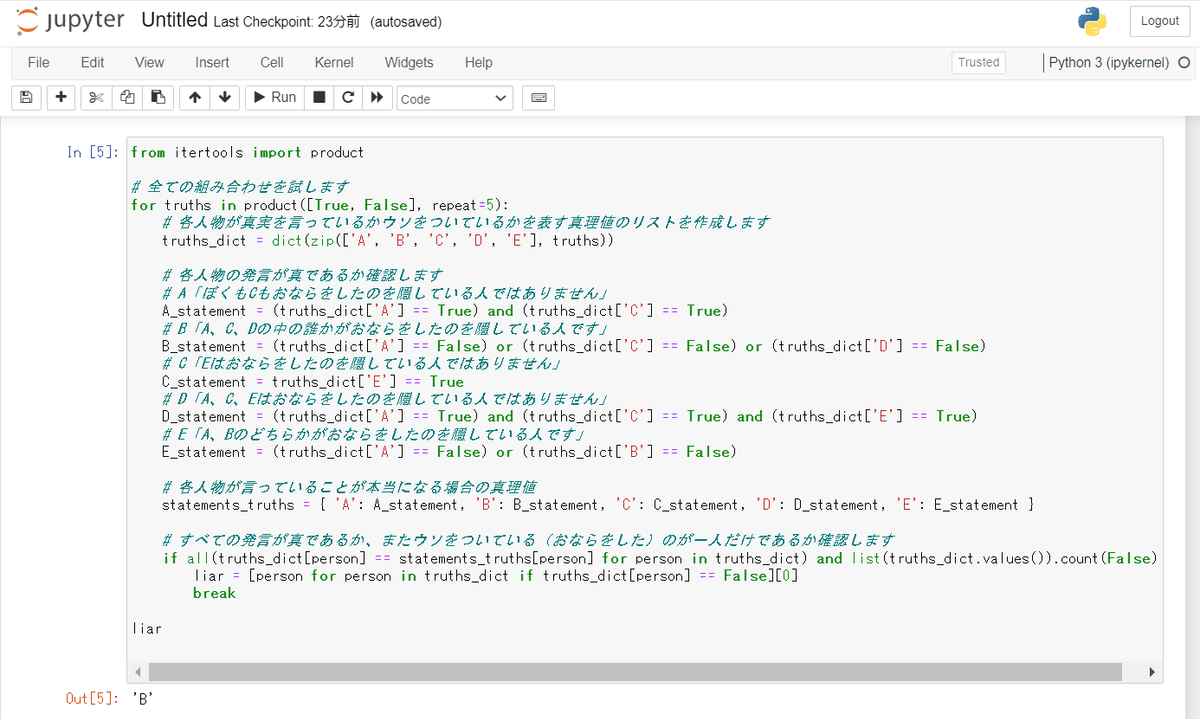
本当にこんな高度なロジックパズルを小学生が習うの?
上の記事で、「ChatGPTは小学生に勝てない!? 子供向け問題を解かせてみた」と言うならば実際の文科省のプログラミングの学習指導要領はどんな物なのか調べてみた。
こちらのページより、小学校プログラミング教育に関する研修教材を調べてみました。ここには3年生向けの教材しか書かれていなかったので、6年生の教材例は以下のサイトから拝借しました。
PGT-4に3年生用6年生用教材を検証してもらったら?
先ず3年生用教材へのGPT-4の評価がこちらです。
この教材は、小学校のプログラミング教育の一環として使用されるようです。特に、ビジュアル型プログラミング言語「Viscuit」を使った実習が中心となっています。
Viscuitは、子どもたちが視覚的に理解しやすいように設計されているプログラミングツールです。この教材では、「たまごをタッチすると割れる」という動きをするプログラムの作成を通じて、プログラミングの基本的な概念を学びます。
具体的には、子どもたちは「たまごを描き、たまごをタッチすると割れる」というプログラムを作成します。さらに、割れたたまごから何かが出てくる動きを追加するなど、自分のアイデアを形にしていきます。子どもたちは作成したプログラムを通じて互いに遊び、気になったプログラムの仕組みを調べて、自分のプログラム作りのアイデアに生かします。
この活動は、子どもたちが自分でプログラムを制御する体験を通じて、プログラミング的思考を育むことを目指しています。また、子どもたちが自分で作成したプログラムを発表することで、プログラミングによって動いている身近なもの(家電製品やゲーム機など)が同じ仕組みで動いていることに気づく機会を提供しています。
なお、この教材は、PC版のViscuitアプリケーションと、学校が所有するタブレットPCを使用して行います。
全体として、この教材は、子どもたちがプログラミングの基本的な概念を理解し、プログラミング的思考を育むためのリソースとして提供されているようです。
つづいて、6年生用の教材のGPT-4の評価がこちら:
1つ目の例では、自動炊飯器のプログラムを考える授業が取り上げられています。子どもたちは、Scratchというビジュアル型プログラミング言語を使って、炊飯の手順を並べ替えます。これにより、条件によってご飯の状態が変わること、そしてそれをプログラムで制御することを学びます。
2つ目の例では、電気の効率的な利用について学ぶ授業が紹介されています。子どもたちは、自分たちが考えた電気の効率的な利用法を、MESHやArtecRoboといったプログラミング教材を使って実現します。これにより、電気の効率的な利用方法について深く理解し、同時にプログラミング的思考も育むことが期待されています。
3つ目の例では、Viscuitという教材を使った授業が取り上げられています。子どもたちは、「噂話が広がる」と「ものを渡す」の違いを理解するために、噂話が広がるシミュレーションをプログラミングします。この活動を通じて、情報と物の広がり方の違いを深く理解し、プログラミング的思考を育むことが期待されています。
これらの例から、プログラミング教育が単にコードを書く技術を教えるだけでなく、問題解決や論理的思考のスキルを育むための手段として用いられることがわかります。また、これらの教材は、子どもたちが日常生活で遭遇する問題や現象に直結しているため、学習の関連性と意味を強調しています。

嘘つきを探すロジックパズルよりもかなり簡単に見えますが
筆者問:上記の小6教材は、嘘つきを探すロジックパズルよりもかなり簡単に見えますがあなたはどうおもいますか?
GPT-4返答:
上記の6年生向けのプログラミング教育の例と「嘘つきを探すロジックパズル」は、異なる種類の思考スキルと理解を養うためのもので、それぞれの難易度はその目的と関連しています。
「嘘つきを探すロジックパズル」は、複雑な論理的推論を必要とします。各人物の発言を分析し、それらが全体の真実とどのように結びつくかを理解する必要があります。これは、論理的思考と複雑な問題解決スキルを鍛えるのに非常に有効な手段です。
一方、上記の6年生向けのプログラミング教育の例は、プログラミングという具体的なスキルとその応用を教えることに焦点を当てています。ここでは、プログラムの作成とその結果を通じて、特定の問題(たとえば、ご飯の炊き方や電気の効率的な利用)を解決することを学びます。これは、プログラミングの基本的なスキルと、それがどのように実世界の問題解決に役立つかを理解するのに非常に有効です。
つまり、これら二つの教材は、それぞれ異なる種類の思考スキルと理解を養うためのものであり、それぞれがその目的に合わせて適切に設計されています。したがって、一方が他方より「簡単」または「難しい」と一概には言えません。
との事。難易度では評価せず「異なる種類の思考スキルと理解を養うためのもの」と結論付けました。
あなたが考える小1から小6までの論理思考問題は?
そこで、筆者はこんな質問をしてみました。
「あなたも間違えた上記のロジックパズルはかなり難易度が高いと思いました。あなたが考える小学1年生用から6年生用までのレベルの論理思考問題を作ってもらえますか? 自然言語による問題とpythonで解を解くコードを教えてください。」
と振って見たら、それはそれは分かりやすい例題をだしてきました。おそらく、論理思考にたけた子なら、これは1学年に続けて学習できる物だと思います。

小学生はトライしてみよう!
では以下にGPT-4制作の論理思考を養うためのpython問題を紹介します。
数当てゲーム:3年生または4年生。ここでは基本的な入力・出力、条件分岐(if文)、およびループ(while文)の基本的な概念を導入します。
あなたが推測した数よりも小さい場合に表示されます。すなわち、プログラムが選んだ「秘密の数」は9より小さかったようです。ですから、最初の推測(9)で "多すぎます!" が表示され、その後の推測でも同じメッセージが表示されました。
このゲームでは、毎回プログラムが1から10までのランダムな数を「秘密の数」として選びます。したがって、毎回のゲームで「秘密の数」は変わります。同じ数を推測しても、ゲームによっては "Too high!"、別のゲームでは "少なすぎます!"、または "おめでとうございます!正解です。" が表示されるかもしれません。
"多すぎます!" が表示された場合、次回の推測でそれよりも小さい数を選ぶと良いでしょう。
import random
def guess_the_number_japanese():
secret_number = random.randint(1, 10)
for _ in range(3): # 3回のチャンスを与えます。
guess = int(input("秘密の数(1から10まで)を推測してください: "))
if guess == secret_number:
return "おめでとうございます!正解です。"
elif guess < secret_number:
print("少なすぎます!")
else:
print("多すぎます!")
return "申し訳ありません、チャンスが尽きました。秘密の数は " + str(secret_number) + " でした。"
guess_the_number_japanese()FizzBuzz問題:4年生または5年生。この問題は繰り返し(for文)、条件分岐(if文)、および基本的な算術演算(剰余演算)について深く掘り下げます。また、この問題を解くことで、数値が特定の条件を満たすかどうかを判断する論理的思考を養います。
"Fizz"と"Buzz"は、プログラミングの教育や学習でよく使われる単語で、特に「FizzBuzz」というゲームで知られています。「FizzBuzz」はプログラミングの初心者がループ、条件文、算術演算などの基本的な概念を学ぶためのシンプルな問題です。
「FizzBuzz」ゲームのルールは次の通りです:
1から順に数を言い出し、その数が3の倍数なら「Fizz」、5の倍数なら「Buzz」、両方の倍数(つまり15の倍数)なら「FizzBuzz」を言います。それ以外の数のときはそのまま数を言います。
例えば、最初の15の数字は次のようになります:
1, 2, Fizz, 4, Buzz, Fizz, 7, 8, Fizz, Buzz, 11, Fizz, 13, 14, FizzBuzz
このゲームはプログラミングの世界で非常に有名で、初心者が基本的なプログラミング概念を理解しているかどうかをチェックするための練習問題や面接問題として使われることがあります。
# 2. FizzBuzz問題
# 自然言語の問題:1から100までの数で、3で割り切れる数には"Fizz"、5で割り切れる数には"Buzz"、3と5の両方で割り切れる数には"FizzBuzz"を出力します。
# Pythonによる解答
def fizz_buzz():
for i in range(1, 101):
if i % 3 == 0 and i % 5 == 0:
print("FizzBuzz")
elif i % 3 == 0:
print("Fizz")
elif i % 5 == 0:
print("Buzz")
else:
print(i)
fizz_buzz()ハングマンゲーム:5年生または6年生。この問題は文字列操作とリストの概念を導入します。また、より複雑なループと条件分岐を使って、ゲームのロジックを実装します。
「ハングマン」のゲームには戦略があります。このゲームでは、ゲームの最初のフェーズでは、言語の一部として最も頻繁に使用される文字から推測を開始することが一般的です。たとえば、英語では、最も頻繁に使用される文字は "e"、次に "a"、"r"、"i"、"o"、"t"、"n"、"s"、"l"、"c" などです。
ゲームが進行するにつれて、部分的に明らかになった単語を見て、可能性のある他の文字を推測します。たとえば、 "_ a _ _ _" が表示されている場合、次の文字として "t"("cat"、"bat"、"rat" など)や "n"("can"、"fan"、"man" など)を推測することが考えられます。
しかし、これらの戦略は、ゲームがランダムな単語を選択するときや、特に長い単語を選択するときには必ずしも有効ではないことに注意が必要です。このゲームは、言葉のパターンを見つけ出すための洞察力と、単語の綴りに対する知識をテストすることを目指しています。
下記はひらがなでプレイできるハングマンゲーム例です。
def hangman_japanese():
secret_word = "あいうえお"
guessed_word = ["_"] * len(secret_word)
attempts = 6
while attempts > 0 and "_" in guessed_word:
print(' '.join(guessed_word))
guess = input("ひらがなを推測してください: ")
if len(guess) != 1:
print("一文字だけを推測してください")
continue
if guess in secret_word:
for i in range(len(secret_word)):
if secret_word[i] == guess:
guessed_word[i] = guess
else:
attempts -= 1
print(f"間違いました。あと{attempts}回のチャンスがあります。")
if "_" not in guessed_word:
return "おめでとうございます!正解は" + secret_word + "でした。"
else:
return "残念、試行回数を超えました。正解は" + secret_word + "でした。"
print(hangman_japanese())