
[mayaで、目で見る、matrix]その3 matrixを扱うノードの紹介(この後の記事への準備!)
matrixを扱うノードの紹介をしてみたいと思います。
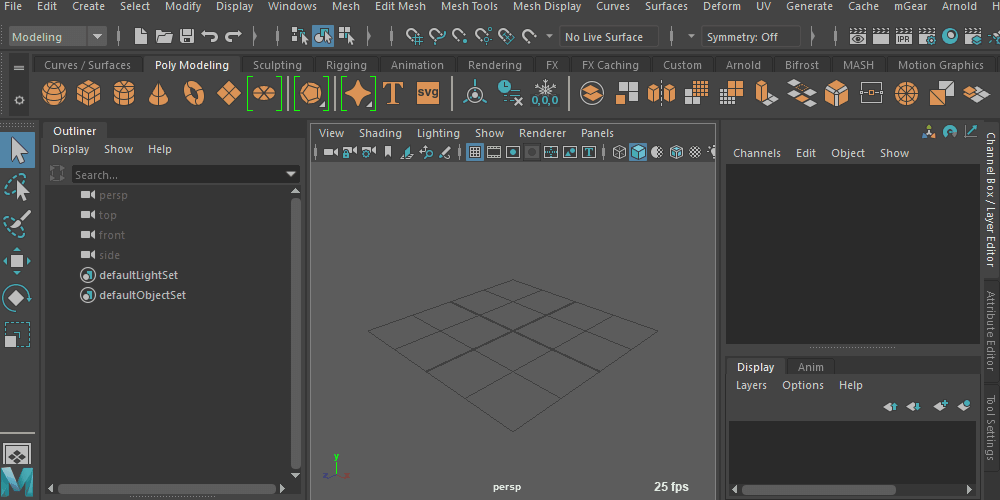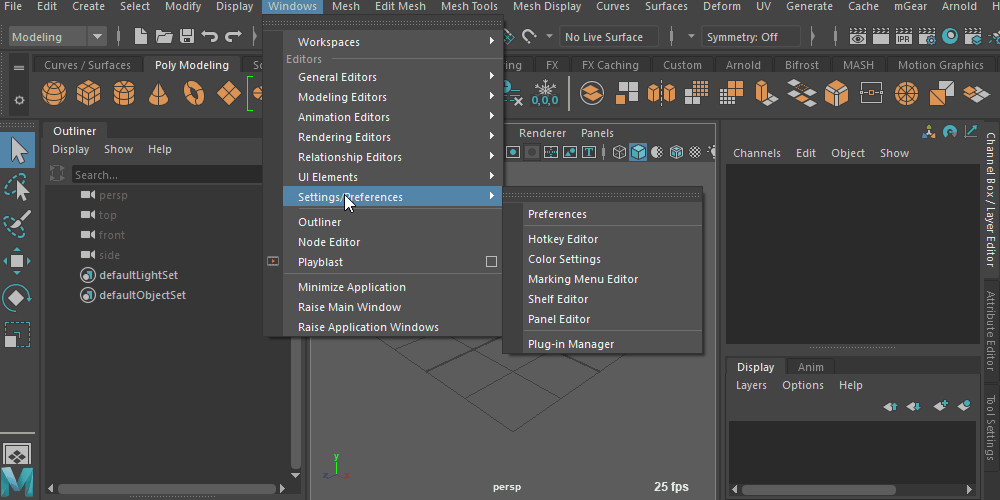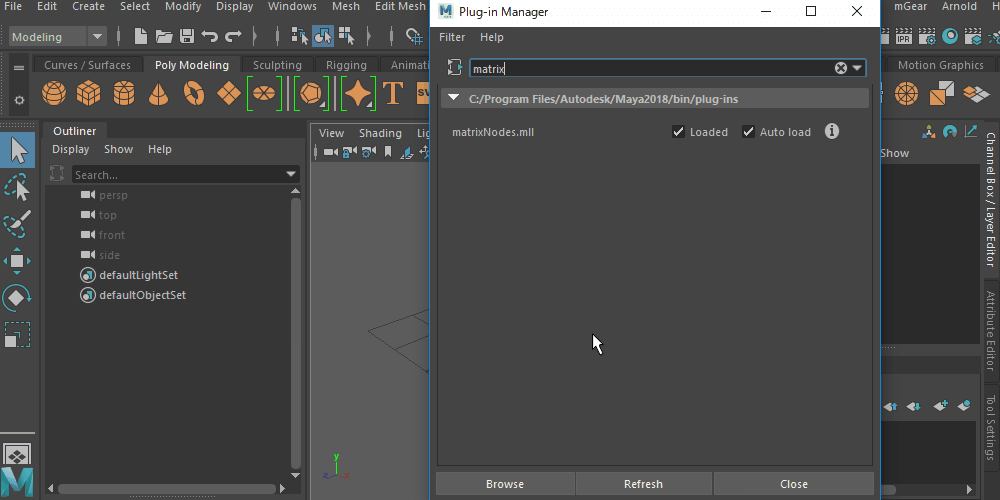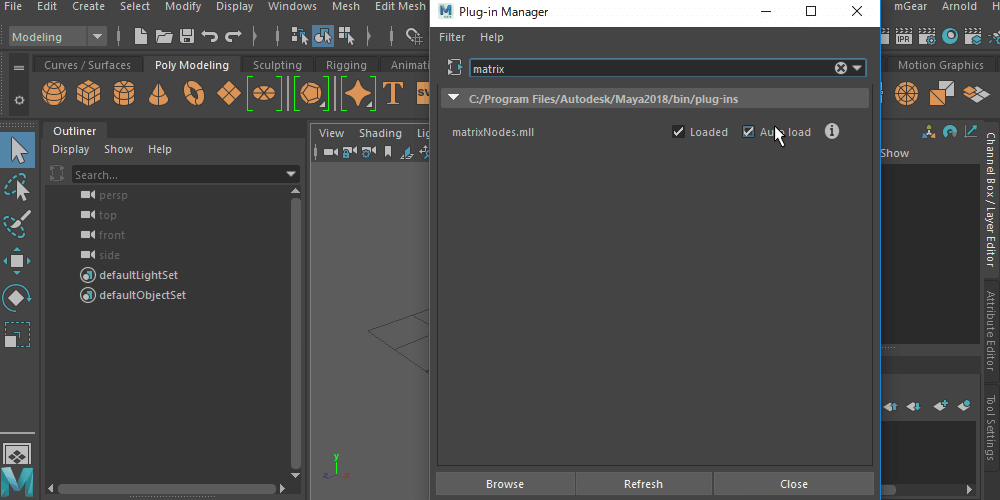
maya標準Plug-in、matrixNodes.mllが読まれていなかったら、ロードを!
ノードを紹介するにあたり、
maya標準Plug-inのmatrixNodes.mllがロードされていない方もいらっしゃるかもしれません。
ノードエディタ等で「matrix」と打って検索しても出てこないな~という方は、まずはPlug-inのロードをしてみてください。
matrixを扱うノード達
「decomposeMatrix」
「composeMatrix」
「inverseMatrix」
「multMatrix」
本記事では、私が使用している上記ノードを、ご紹介したいと思います。
※いやいや、matrix使用する上で、このノード使用してないなんてありえんじゃろ…。。
という方、ぜひご教授お願いいたします!
decomposeMatrix

matrixを下記アトリビュートに変換してくれるノードです。
matrixを扱う上で、いつもお世話になります。
「移動(translate)」
「回転(rotate)」
「スケール(scale)」
「シア(shear)」
「クォータニオン(Qaut)」
composeMatrix

「移動(translate)」
「回転(rotate)」
「スケール(scale)」
「シア(shear)」
の値をmatrixに変換してくれるノードです。
attribute ⇔ composeMatrix ⇔ matrix ⇔ decomposeMatrix ⇔ attribute
特定のアトリビュートのみのmatrixを作成したい時に、重宝します!
dagノード(トランスフォームノード等)を作成する代わりに使用したりします。
本シリーズ記事では、その内いっぱいお世話になります。
inverseMatrix

リセットする値が欲しい!時に、重宝するノードです。
主に親のmatrixを打ち消すことに使用しますが、多方面で活躍してくれるノードです。
matrixの逆行列を返してくれます!
…というと分かりにくいので、受け取ったmatrixを、
「移動(translate)」 0, 0, 0
「回転(rotate)」 0, 0 ,0
「スケール(scale)」1, 1, 1
「シア(shear)」 0, 0 ,0
に戻すことができる値(matrix)を返してくれます。
うぬ。。これも分かりにくい気がするので、目で見てみましょう!
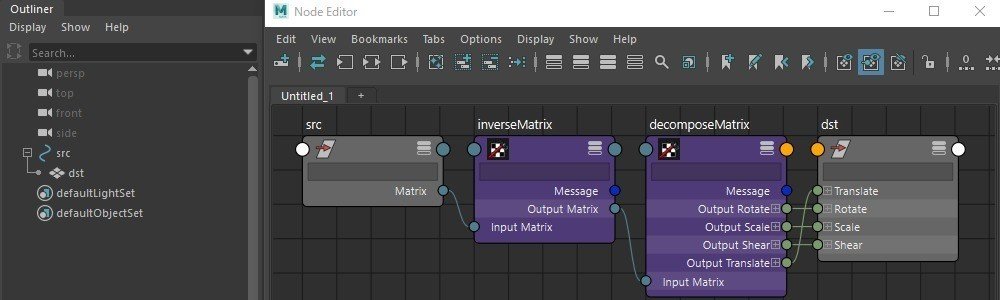
上記設定をした、階層を作成しました。
①srcの子階層にdstがある。
②srcのmatrixをinverseしたものをdecomposeし、dstのアトリビュートに接続する。
(=srcのアトリビュートに設定された値を打ち消す(元に戻してくれる)値をdstに接続する)
srcが「十字」で、dstが「キューブ」です。

srcのアトリビュートの値を打ち消す値を、
dstのアトリビュートにコネクションしているので、
srcがどれだけ動いてもdstは一切動きません。
matrixをinverseすると、リセットする値を返してくれます。
※上記で行ったコネクションは、下記画像と同じ処理になります。

トランスフォームノードのmatrixをinverseMatrixにコネクションして返されたmatrix = トランスフォームノードのinverseMatrixのmatrix
inverse処理したmatrixは、トランスフォームノードは、既に持っているんですね。
multMatrix
matrixの階層計算をしてくれるノードです。
matrixを扱う上で、このノードが肝になります。
(= matrixを扱う上で、階層を理解することが肝になる!…と思います。)
ターゲット(src)の座標を取得する
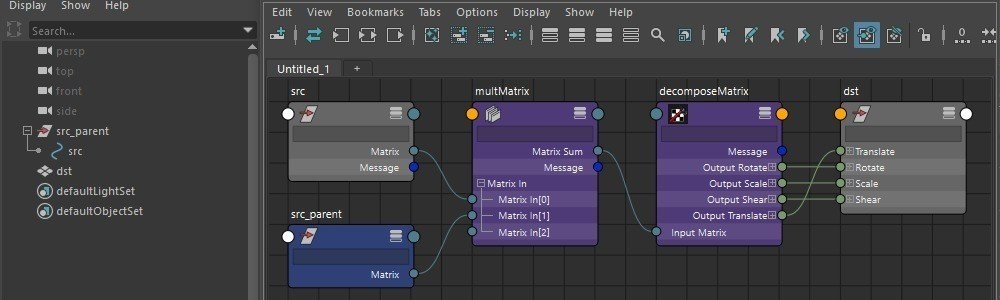
上記設定をした、階層を作成しました。
①srcの親階層にsrc_parentがある。
②srcとdstの共通の親であるトップ階層(world階層)にdstがある。
③srcとsrc_parentのmatrixをかけたものをdecomposeし、dstのアトリビュートに接続する。
(=srcの座標値(matrix)をdstに接続する)
うぬ。文字を読んでいてもよく分からないので、目で見てみましょう!
srcの動きと、dstの動きが同じになります。

大事なのは、ターゲット(欲しい座標)が先頭になること
matrixの階層計算(=multMatrix)するにおいて、欲しい座標(ノード)を一番先に接続する!
この手順が重要になります。
ターゲットを一番先に接続して、その親、その親……と順番にmatrixを掛けていきます。
うぬ。なぜ順番が大事なのか…。。
mult(multiply) = 掛け算。
掛け算と考えると、
1 × 2 = 2
2 × 1 = 2
で、どっちの順番で掛けても、結果は同じ!
なのですが、matrixの掛け算は結果が違います。
トランスフォームノードを構成する階層(移動/回転/スケール)で、アトリビュートの階層順番が違うと、結果が違ったと思います。
それと同じこと!と思っていただくと分かりやすい(かも…?orz)と思います。
dstに親がいれば、inverseを掛けて、なかったことに

dstの親にトランスフォームノード(dst_parent)を追加しました。multMatrixには、dst_parentのinverseMatrixを最後尾に接続しました。

inverseMatrixノードの項でやったことと同じですね。
inverseMatrixを掛ければ、自ノードの変化した座標を打ち消す値を返してくれます。
なので、今回やったことは、
srcの座標は取得する。そのうえで、dstの親の座標は打ち消す。
(= srcの座標(matrix)をdstに接続する)
srcに親がいっぱいいれば、matrixを掛け続けて、座標を取得。
dstに親がいっぱいいれば、inverseMatrixを掛け続けて、すべてをなかったことに…!


やることは同じで、数が変わるだけです!
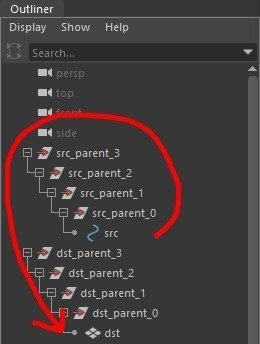
ターゲットであるsrcのmatrixから順番に、
親、その親…とmatrixを掛けていきます。
共通の親(今回は、トップ階層(world階層))まできたら、
dstの一番の親から順番にdstに向けて、
子、その子…とinverseMatrixを掛けていきます。
まとめ
matrixを扱ううえで、頻出するノードのご紹介でした。
愛おしい子達ですね!
「decomposeMatrix」
は、matrixを移動等のアトリビュートに変換する。
「composeMatrix」
は、移動等のアトリビュートをmatrixに変換する。
「inverseMatrix」
は、matrixをリセットしてくれる値のmatrixを作成する。
「multMatrix」
は、階層計算してくれる。
