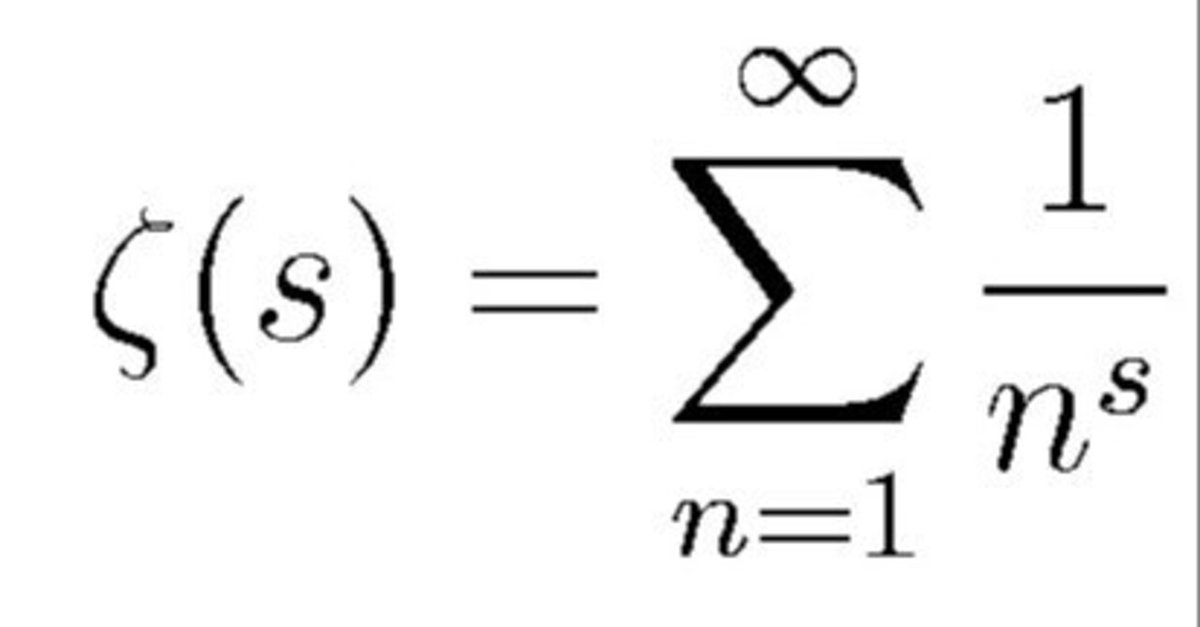
Riemann's zeta function
$$
\begin{array}{|c|}
\hline\\
\text{Definition of Riemann zeta function for real variable} \text{ for s} >1 .\\
\zeta (s) = \displaystyle \sum_{k=1} ^{\infty} \frac{1}{k^s} \space\space \space \space \text{for s> 1}\\ \\ \hline
\end{array}
$$
$$
\begin{array}{|c|}
\hline\hline\text{\space }\\
\text{Well Definition of Riemann zeta function} \zeta(s) \text{ for real variable}\\
S_{n}(s) \to \zeta(s) \\
\text{ where }
S_{n}(s) = \displaystyle \sum_{k=1} ^{n} \frac{1}{k^s} \space\space \space \space \text{for s> 1}\\ \\ \hline
\end{array}
$$
We will show convergence of rea Riemann zeta function for $${ s >1 }$$ .
Let $${ S_{n}(s) :=\displaystyle \sum_{k=1}^{n} \frac{1} {k^s} \space\space \space \space for \space \space \space s >1 }$$
It is clear that $${ S_{n} (s) }$$ is monotone increasing for n.
$$
S_{n} (s) - S_{n-1} (s) = 1/ n^s = 1 * 1/ n^s < \int_{n-1} ^{n} \frac{1} {x^s}dx
$$
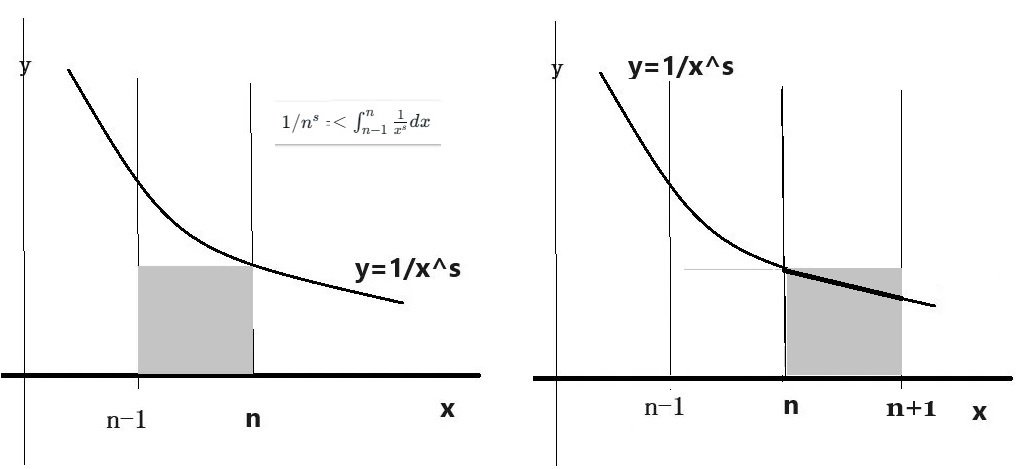
Remark $${ S_1 (s) =1}$$ and
$$
\begin{array}{ccl}S_n(s)&<&\small1 +\int_{1}^{n} \frac {1} {x^s} dx \\
& = & \small 1+\Large\lbrack\frac {x ^{-s+1} }{-s+1} \Large\rbrack_{1}^{n} \\
& = & \small 1+ \frac {n^{-s+1} }{-s+1} - \frac {1^{-s+1} }{-s+1} \\
& = & \small1 - \frac {1}{n^{s-1} (s-1)} +\frac {1}{s-1} \\
& < & \small1+\frac {1}{s-1}\end{array}
$$
The following inequality can also be derived using a similar method.
$$
\begin{array}{ccc}
S_n(s)&>& S_{n-1}(s)>\int_{1}^{n} \frac {1} {x^s} dx \\
&=&\Large\lbrack\frac {x ^{-s+1} }{-s+1} \Large\rbrack_{1}^{n} \\
&=&\frac {n^{-s+1} }{-s+1} - \frac {1^{-s+1} }{-s+1} \\
&=&\frac {1}{s-1} -\frac {1}{n^{s-1} (s-1)} \\
&=& \frac {1}{s-1}(1 - \frac {1}{n^{s-1}})
\end{array}
$$
Therefore we have next two properties.
$$
\begin{array}{|c|}\hline \hline\\
\hspace{1cm}\frac{1}{s-1}-\frac {1}{n^{s-1} (s-1)} < S_n(s) <
1+\frac {1}{s-1} \text{for s>1} \\ \\
\lim_{n\rightarrow \infty} S_n(s) = \zeta(s)\\ \\
\lim_{s\rightarrow +0} (s-1) \zeta(s) =1 \\ \\
\hline\end{array}
$$
$$
\begin{array}{|c|}\hline \\
\text{ Uniformly convergence of } \zeta(s)
\text{ for } s \ge1+d, d>0 \\\\
\hline\end{array}
$$
(proof)
Let $${M_k = k^{-1-d}}$$ . Then
$$
\begin{array}{c} \\
\frac{1}{ k^s} < \frac {1} { k^{1+d}} = M_{k} \\
\displaystyle\sum_{k=1}^{\infty} \frac{1}{ k^s}
< \displaystyle\sum_{k=1}^{\infty} \frac{1}{ k^{1+d}} = \displaystyle\sum_{k=1}^{\infty} M_{k} = \zeta(1+d) \\
\end{array}
$$
$${\sum_{k=1}^{\infty} M_{k} }$$ converges to $${\zeta(1+d) }$$ so , by Weierstrass M-test , $${S_{n}(s) }$$ converges to $${\zeta(s) }$$ uniformly for $${s \ge 1+d }$$
