
Nelder-Mead法 with Gnuplot(Go言語)
今回は,
「Go言語でこんなこともできちゃいます!」シリーズの第一弾です!
(↑誰がやるって言ったんや...w)
とりあえず,Goの文法シリーズを最近,投稿しておりましたが,
「そもそも,何のためにGoを勉強すんねん!わいも暇やないぞ!」
って思っちゃう人のために,(←この気持ちはよくわかる...)
Goの魅力や学習によるメリット
を伝えていく投稿も,ボチボチやっていこ~と思います!
そして,今回は...
Nelder-Mead法 with Gnuplot
ということで,
gnuplotというグラフ描画ツールと連携して,
Nelder-Mead法という計算科学の最適化アルゴリズムを視覚的に理解しよう!
というテーマでやっていこうと思います.
今回作成したプログラムでは,下記のパッケージを使用しました.
【パッケージ①:go-gnuplot】
・Go言語からgnuplotと連携するためのパッケージ
・Go言語からgnuplotへ命令を転送し,gnuplotにグラフを描画させます.
・タイトルの画像や下のGif動画は,gnuplotに作成してもらいました!
【パッケージ②:gonum】
・Go言語で書かれた数値計算用のパッケージ
・optimizeフォルダにNelder-Mead法のアルゴリズムがあります.
それでは,Go!
gnuplotとは
gnuplotは「ニュープロット」や「グニュープロット」などと呼ばれます.
世界的には,「ニュープロット」が一般的だそうですが,
日本では,「グニュプロット」って呼んでる人が多い気がします!
そして,gnuplotに関しては,下記サイトを参考にしてください。
(伝家の宝刀,うぃきぺでぃあー!)
まぁ,簡単に説明すると,こんな感じです!
・よく研究者や工学系の大学生が使います.
(私も学生時代に使っておりました.)
・CLIインターフェースでコマンドを入力して,グラフを作成します!
(はい,難しい単語:CLIというのが出てきましたね...)
(要するに,コマンドプロンプト↓と同じってことです.)

(上図の左がコマンドプロンプト,右側がgnuplotです.)
(「plot x*x」と入力すると,グラフが描画されます.)
・二次元だけでなく,三次元のグラフも作成できます.
・テキストファイルにプロットデータを格納して,テキストファイルからプロットもできます!
・だいたいのプログラミング言語から,パイプを利用してgnuplotを起動させ,コマンドを送信し,gnuplotにお絵描きさせることができます!
Nelder-Mead法とは
関数の最小値を探索するためのアルゴリズムです!
ちなみに,「最小値を探索する」と言っても,
必ず最小値がわかるわけではないので,ご注意ください!
(本ノートでは,実例をもとに解説しております.)
また,最適化アルゴリズムには「Nelder-Mead法」以外にもたくさんあるのですが,私は実用に耐えうる最適化アルゴリズムの一つとして,「Nelder-Mead法」を押します!
というのも,
Nelder-Mead法は関数の勾配(微分値)が不要なアルゴリズムだからです
世の中には,微分値が事前に分からない最適化問題が山ほど存在します.だから,「Nelder-Mead法」の威力が発揮されます!
まぁ,関数の勾配が分からなければ,
有限差分法
とか使えば,なんとかなるのですがね!
( どんどん,話が専門的になって,
読者が離れていきそうなので,この辺で... (;´Д`) )
そして,「関数とか私に関係ないわ!」とか思った,そこのあなた!
あなたの身の回りにある賢い商品たち,たとえば,
AI,ロボット,カーナビ,...その他シミュレーション(ざっくり)では,
複雑な関数の最小値を探す必要がめちゃめちゃ出てきます!
「よい ソフト or 成果 を生む = 如何にして関数の最小値を求めるか」
みたいな世界は確かに存在するのです!
今後,
このような知的なお仕事につきたい!って人や,
研究で使いたいって方には,
ぜひ最後まで読んでほしいですね!
(難しい数式の説明は今回はしません.視覚的に解説します.)
なお,詳しくはこちらのサイトを参考にしてください.
(伝家の宝刀,うぃきぺでぃあー! 二回目,お許しください m(__)m )
それでは,Nelder-Mead法を視覚的に理解しましょう!
爆速:Nelder-Mead法を視覚的に理解せよ①
さーて,今回の説明用ソースコードはこちら!どーん!
みたいなことは,本日は致しません!
ソースが長くなるし,説明が大変なので...
みんなのレスポンスが良ければ,説明用のノートを作ります('ω')
ということで,説明用ソースコードから出力された
下のGif動画をご覧ください。これがNelder-Mead法だ!

うーん,
アメーバみたいなやつが関数の凹部に収束していくプロセス
が分かりますねぇ~
アメーバみたいなやつは,「シンプレックス(単体)」と呼ばれます.
今回は,二変数関数
z = f(x,y) = x*x + y*y
の最小値を,Nelder-Mead法で探索しています.
最小値は「原点(x,y)=(0,0)」となります!
そして,最初(iteration=1)のシンプレックスは小さいのに,凹部へ収束する過程で,シンプレックスが「膨張」しているのがわかるでしょうか?
Nelder-Mead法では,シンプレックスが現在いる場所から,より遠くの場所に低い場所(関数値)を見つけると,シンプレックス自身を膨張させ,探索の一歩をでかくします!(自分を大きくして,探索回数を減らしているのですね...賢いアメーバ!)
そして,シンプレックスの現在位置から見て,周りの場所(関数値)が高くなれば,自分は凹部にいると判断し,「収縮」します!
「収縮」が続くと,シンプレックスは一点に収束し,探索終了となります!
爆速:Nelder-Mead法を視覚的に理解せよ②
次は,目的関数に障害物を追加し,アメーバ君がどのような反応をするのか,いじわるしてやりましょう!( *´艸`)
あっ,ちなみに「目的関数」とは,最適化問題でよく使われる言葉で,
最小化 or 最大化 (=最適化)の対象となる関数
を指します.①の説明で,目的関数は,
z = f(x,y) = x*x + y*y
となります!

ぐぬぬ( ゚Д゚) 賢いですね!
見事に,障害物を避けて,関数の凹部に収束しております!
爆速:Nelder-Mead法を視覚的に理解せよ③
②までは,最小値が原点(x,y)=(0,0)でしたが,
今回は,最小値を(x,y)=(-1.5,-1.5)付近に設定した目的関数でアメーバ君の挙動を見ていきましょう!

ぐぬぬぬ( ゚Д゚) 賢いですね!
アメーバ君の触手が反応してしまい,見事に関数の最小値を探索できました!
爆速:Nelder-Mead法を視覚的に理解せよ④
これで,最後です!
アメーバ君の触手が反応できないような,少し遠い場所に最小値を移動してみて,アメーバ君の反応を観察してみましょう!
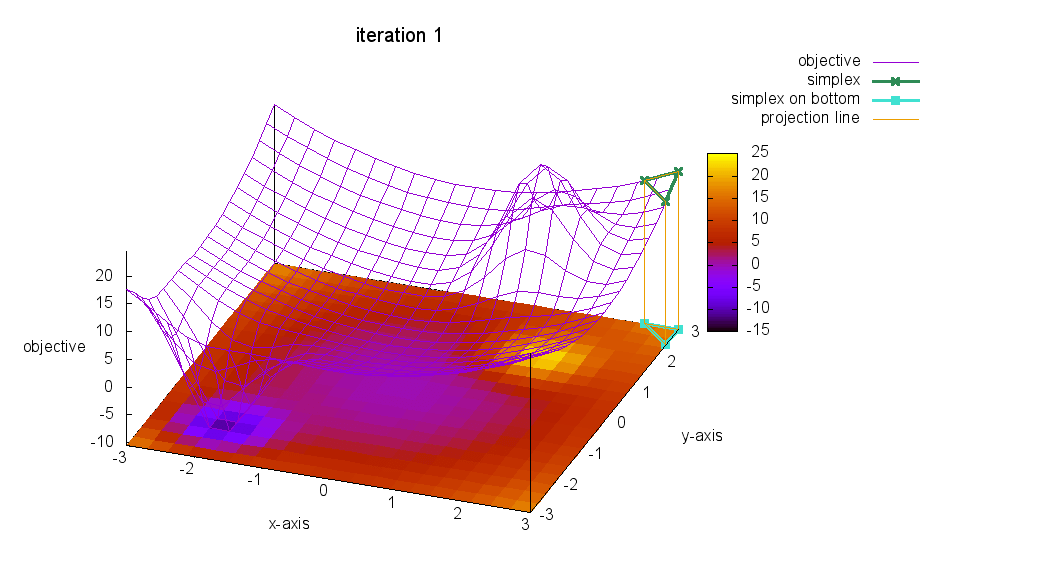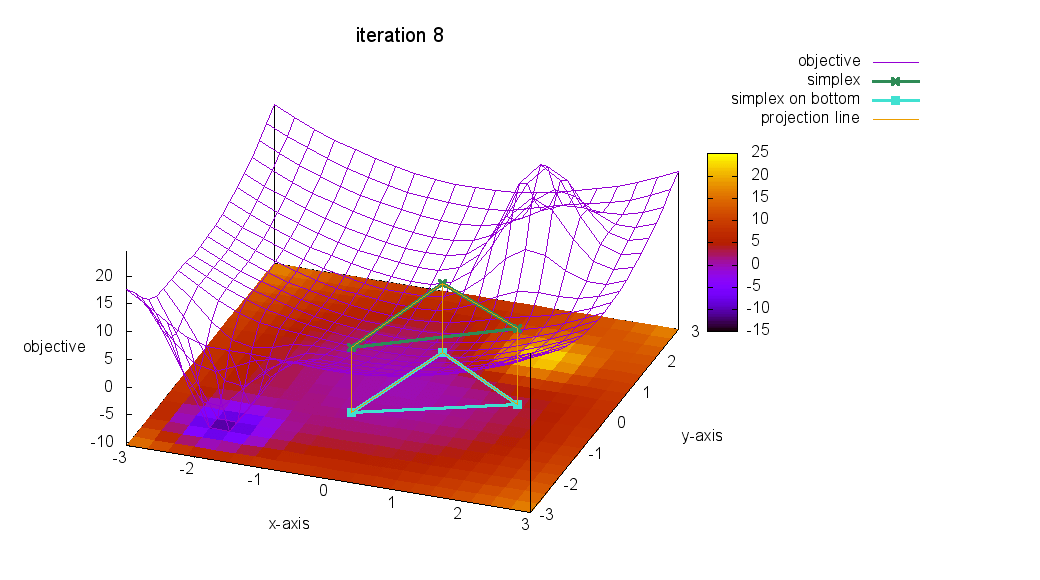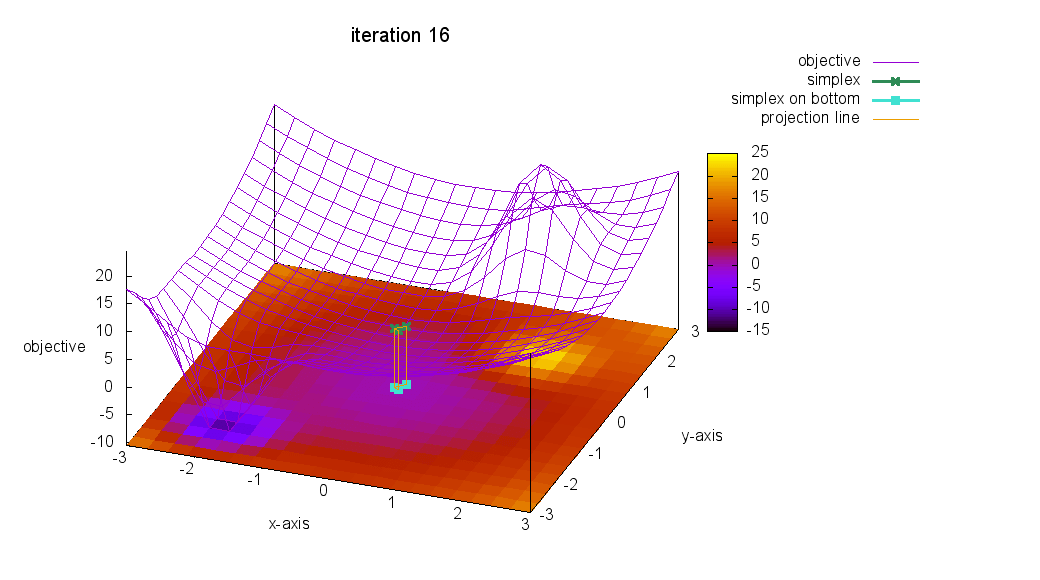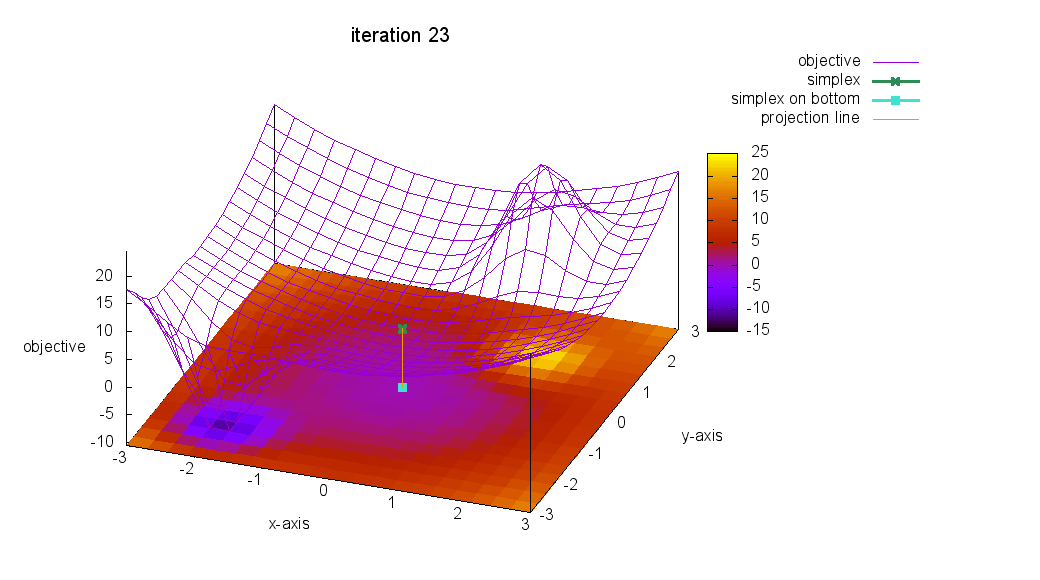
ぷぷっ( ´∀` ) 所詮,アルゴリズム! まぁ,こんなもんです!
Nelder-Mead法を含めて,多くの最適化アルゴリズムは
極値へ収束するアルゴリズムなのです!
最小値ではありません!
うえの例を見ても,分かるように最適化アルゴリズムの多くは,
初期値が重要となります.
たとえば,上の例では,(x,y)=(-1,-1)付近から,かつ,シンプレックスをそこそこ大きくして,Nelder-Mead法を実行していれば,最小値を発見できたはずです!
ということで,Nelder-Mead法では,多点探索を行ったりします.
要するに,適当な複数の初期値から,Nelder-Mead法を実行して,極値を探索します.そして,探索した極値の中から,最も小さい値を”最小値”とするのです!
(まぁ,確証はないけど,これを最小値にしよっと!って感じです...w)
終わりに
いかがでしたでしょうか?
とりあえず,Goでは,
世界中の誰かが毎日,パッケージを作成しており,
その恩恵を受けることができちゃうのです!
そして,プログラミングはボチボチやってきたけど,
数値計算は初めて!っていう人も多かったのではないでしょうか?
( Nelder-Mead法が初めの数値計算... とんでもない第一歩ですねw )
プログラミングをできる人は数多くいますが,ここら辺の理論に,詳しくなり,使いこなせる人は少ないと思いますので,市場での希少価値(給料)UPにつながると思います!
これを機に数値計算を勉強してみるのも良いですねぇ~(*'ω'*)
とりあえず,今回の成果物(gifファイル)の作成に使ったソースコードは一切,記載しておりません.皆さんのレスポンス次第で,本ノートの解説を作成・投稿するかどうかを決めたいと思います!
(全部の解説は大変なので,
どこら辺が知りたいか教えてくれたら幸いです!)
それでは,本日はこの辺で!('ω')ノ
パタパタパタ....(←アメーバ君のように)
サポートお願いいたします.主に初心者から中級向けに,ソフトウェア開発に関する知識を提供していきます.

