『直線で曲線を描くやつ』を掘り下げてみよう

先日 ▲ こちらの記事を書かせていただきました。
そこでとある方に僕の記事を紹介していただいたのですが、その際『直線の傾き』を話していらっしゃったんですよね。

僕も少しは触れましたが、本題はどちらかというと交点のほうでした。
しかし、急に興味が出てきました。
これも曲線の式みたいに一般化できるんじゃね？　と。

ということでやっていきましょう！！
この記事は前回の内容は把握済みであることを前提としています！　まだ読んでないけど、って方はぜひどうぞ。↑

さて、今回やりたいのは、
前回やった ▼ こちらのグラフの微分係数を全部調べたい。
導関数と呼べるかはちょい微妙。媒介方程式の微分は習ってない。あるの？

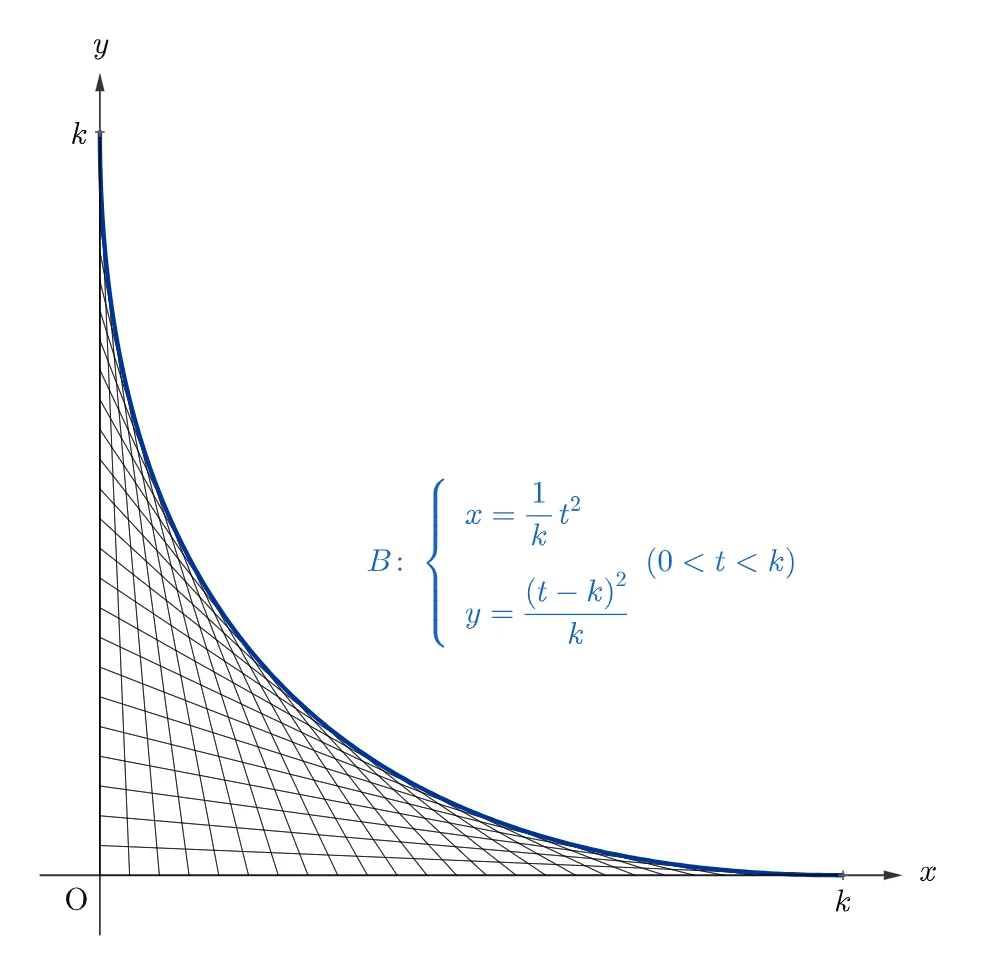
ということで、前回のごとく変数設定をしていきましょう。
$${k}$$は前回と同じく全体の図形の大きさで、
$${t}$$は適当な線を引く$${x}$$座標、$${\epsilon}$$はなにかしらの正の数です。

傾きを求めるには２つの点が必要。ということでこちらをご用意しました。

色が薄いのは申し訳ない。どうしてもこれを強調したかったんです。
前回使った式を用いて、あのちっちゃい点二つの座標を求めてしまいましょう。
$${t-\epsilon}$$と$${t}$$との交点を$${\text{A}}$$、$${t}$$と$${t+\epsilon}$$との交点を$${\text{B}}$$とします。

$${\text{A}\!:\;l(x,\;t-\epsilon)=l(x,\;t)}$$
$${\displaystyle\frac{t-\epsilon-k}{t-\epsilon}(x-t-\epsilon)=\frac{t-k}t(x-t)}$$
$${t(t-\epsilon-k)(x-t-\epsilon)=(t-k)(t-\epsilon)(x-t)}$$
$${\{t(t-\epsilon-k)-(t-k)(t-\epsilon)\}(x-t)=\epsilon t(t-\epsilon-k)}$$
$${\epsilon k(x-t)=\epsilon t(t-\epsilon -k)}$$
$${\displaystyle x=t+\frac{t(t-\epsilon-k)}k,\;\;\;\;y=\frac{(t-k)(t-\epsilon-k)}{k}}$$

$${\displaystyle\therefore\;\text{A}\left(t+\frac{t(t-\epsilon-k)}k\:,\;\;\frac{(t-k)(t-\epsilon-k)}{k}\right)}$$

$${\text{B}\!:\;l(x,\;t)=l(x,\;t+\epsilon)}$$は前回やったので計算過程は省略して
$${\displaystyle\text{B}\left(t+\frac{t(t+\epsilon-k)}k\:,\;\;\frac{(t-k)(t+\epsilon-k)}{k}\right)}$$

さて、傾きを求めるってことは線分$${\text{AB}}$$に対して$${\displaystyle\frac{\,\Delta y\,}{\Delta x}}$$を求めるということ。

求めちゃいます。
$${\displaystyle\;\;\;\;\frac{\,\Delta y\,}{\Delta x}=\frac{\,y_\text{B}-y_\text{A}\,}{x_\text{B}-x_\text{A}}=\frac{\:\displaystyle\frac{(t-k)(t+\epsilon-k)-(t-k)(\,t-\epsilon-k)\,}{k}\:}{\displaystyle\frac{t(t+\epsilon-k)-t(\,t-\epsilon-k)\,}{k}} \\ =\frac{2\epsilon(t-k)}{2\epsilon t}=\frac{\,t-k\,}{t}}$$

……って、これ$${l(x,\;t)}$$の傾きと一緒じゃないですか。
う～ん、よく見てみればわかるものを。無駄足が過ぎる……。
まぁでも、最初は$${\epsilon \longrightarrow 0^+}$$とかするつもりでいたのでだいぶびっくり。

……え～と、ここからどうしましょうか。
これを～……。$${y}$$のほうに持っていくか？

そんで$${x}$$のほうは……。$${\text{A}}$$の$${x}$$座標にある$${\epsilon}$$を$${0^+}$$に持っていくとできそう……
か？　まぁやってみよう。$${\displaystyle\lim_{\epsilon\to0^+}\left\{t+\frac{t(t-\epsilon-k)}k\right\}=t+\frac{t(t-k)}k=\frac{\,1\,}kt^2}$$

ということで、先ほどの曲線 $${B}$$に対して$${(x,\;m(B(x)))}$$の集合は
曲線$${M\!:\;\begin{cases}x=\displaystyle \frac{\,1\,}kt^2 \\\;\\\displaystyle y=\frac{\,t-k\,}t\end{cases}\;\;\;\;(0< t< k)}$$
と言えるでしょう。
……不安なのでちょっとGeogebraで検証してみます。

……お、できてました！　よかった～。
図の説明を少ししておくと、
緑色のグラフが先ほど求めた傾きを全範囲で求めたやつ、
赤色の線は任意の曲線$${B}$$の上の点$${\text{F}}$$での$${B}$$の接線、
オレンジ色の線は接線の傾きをそのまま$${y}$$座標にした定数関数のグラフ。

ここで点$${\textbf{F}}$$の$${\bm{x}}$$座標と、曲線$${\bm M}$$と直線$${\bm{y=l'(x)}}$$の交点の$${\bm{x}}$$座標が同じならば
点$${\textbf{F}}$$での傾きを曲線$${\bm M}$$の方程式が説明できているということになる。
画像を見てもらえたらわかる通りちゃ～んと$${x}$$座標同じなので、成功です。
や　っ　た　ぜ　！！！！

これを陽関数の形で表すことはできるのでしょうか……。
ちょっとやってみましょう。

$${x=\displaystyle \frac{\,1\,}kt^2,\;\;\;t=\sqrt{kx}\;\;\;(\because\,x>0)}$$
$${y=\displaystyle\frac{\,t-k\,}t=1-\frac{\,k\,}t,\;\;\;y=1-\sqrt{\frac{k}{\,x\,}}}$$

あれ、あっさりできた……。ということは$${B}$$のほうも？
やってみましょうか。

$${x=\displaystyle\frac{\,1\,}kt^2,\;\;t=\sqrt{kx}\;\;\;(\because\,t>0)}$$

$${\displaystyle y=\frac{(t-k)^2}k=(\sqrt{x}-\sqrt{k})^2\;\;(0< x< k)}$$ 

……できちゃった。というかなんだこれ。一応代数関数ではありそう。

……うん。ちゃんとグラフも重なる。よかった～～～～～～～。

いかがだったでしょうか。……予期せぬ展開に記事が飛び散って僕自身も少し困惑しています。
媒介方程式を陽関数に直す（『媒介変数の消去』と言うそうです）のは初めてやってみたんですけど、慣れれば楽しくなりそうですね。

では、また次の記事でお会いしましょう。
間違いやご意見などございましたらコメントにて！
YKでした :D