
バックテストの評価指標まとめ
バックテストの評価指標とはバックテストによって集まった損益データを見やすい形にまとめたものです。システムの実力を推定したりするわけではなく、バックテスト結果そのものを評価するため、統計学の言葉にすると記述統計に当たります。
評価指標の意味を知ることや計算式を知ることはバックテストする人にとって基本ですが、今回はさらに一歩踏み込んだところまで解説します。
◆期待利得
「1取引あたりの損益」という形でリターンの大きさを表す指標であり、損益データの平均値とも言えます。
計算式


純損益がプラスであれば期待利得はプラスとなり、純損益がマイナスであれば期待利得はマイナスとなるので期待利得は0が閾値と言えます。EAの期待利得が0以上であれば、トータルでプラスということになります。
グラフで見る期待利得の特徴

これは、あるEAのバックテストから「1トレード毎に変化する期待利得の数値」をグラフ化したものです。取引数が少ないときは偶然のノイズによる上下の振れ幅が大きいですが、取引数が増えると安定した数値になっていくことがわかります。ある程度の取引数(サンプルサイズ)があれば期待利得によるシステムの評価が可能だと言えます。

次に複利運用したときの「1トレード毎に変化する期待利得の数値」をグラフ化します。先ほどの単利運用のグラフと違って取引数が増えても、期待利得の数値が安定していません。ロットサイズの規模が一定でないため、ロット数が大きいトレードの損益に強い影響を受けて、期待利得の数値が安定しないことが原因です。
この特性により期待利得は基本的に単利運用のバックテストデータしか正しく評価できないことになります。複利運用のデータを評価するときには、損益を単利運用に換算したデータに計算しなおしてから期待利得を算出する必要があります。
◆プロフィットファクター(PF)
利益合計と損失合計の割合を計算したものです。期待利得が「1取引あたりの損益」という形でリターンの大きさを表す評価指標であったのに対して、PFは「損失1に対する利益の大きさ」という形でリターンの大きさを表す指標だと言えます。
計算式


利益合計より損失合計が大きければPFは1.0を下回るため、1.0が閾値となります。ネットなどでよくPFは2.0以上が良いとか1.5以上が良いとか言われますが、1.0以外の基本的に明確な閾値はありません。数値の良し悪しは「何と比較するか」「どんな条件か」によって変わります。
ランダムなトレードのPFとの比較
ランダムなトレードでは、スプレッドなどの取引コストを考慮しないとき「PF=1.0」に収束することになりますが、実際には偶然起こる振れ幅があります。
取引数がnとすると片側95%の確率でランダムなトレードのPFの偶然起こりうる上振れ値は次の式になります。

この式にEAのバックテストの取引回数をnに代入して計算し、計算結果よりもバックテストのPFが高ければ、そのEAに優位性がある可能性が高いと言っていいでしょう。

補足としてランダムなトレードのPFの偶然起こりうる上振れ値が上の式になる解説を載せておきます。

このランダムなトレードのPFの偶然起こりうる上振れ値を求める計算はEAのOnTester関数内で行い、Print関数で計算結果を出力すると便利です。
まず#includeでMath.mqhを読み込んでおいてください。※MQL5です。
#include <Math\Stat\Math.mqh>OnTester関数の中でこのコード記述します。
//--- 単一バックテストのみ
if(MQLInfoInteger(MQL_TESTER) && !MQLInfoInteger(MQL_OPTIMIZATION))
{
double x = 1.64; // ←厳しく評価するなら 1.96 や 2.58 などにする
double PF = TesterStatistics(STAT_PROFIT_FACTOR);
const double n = TesterStatistics(STAT_TRADES);
//--- ランダムなトレードのPFの上振れ値の計算
x = (n + x * sqrt(n)) / (n - x * sqrt(n));
x = MathRound(x, 2);
//--- バックテスト結果のPF
PF = MathRound(PF, 2);
Print("ランダムなトレードのPFの上振れ値 ≦ ", x, " バックテスト結果のPF = ", PF);
}単一バックテストの終了後に操作ログに計算結果が出力されます。

◆悲観的リターンレシオ(PRR)
悲観的リターンレシオ(PRR)はPFを元に考案された指標で、「取引数(サンプルサイズ)が多いほど高く評価するPF」と言えます。
計算式

PRRは常にPFよりも低い値となり、取引数が無限に大きくなるとPFに近づきます。
最適化結果のパフォーマンスを測る尺度
PRRについてはラルフ・ビンス(著)「投資家たちのマネーマネジメント」で詳しく解説されています。異なるパラメータ値でも実行結果の比較(最適化など)に適した指標です。

取引数が多いほどポジティブな結果を示すPRRは、例えば先月のフォワードと去年のフォワードの比較のように期間が違うものどうしでの評価や、別々のEAどうしの比較には適していません。
取引頻度が高いEAを優秀だと判断するために作られた指標ではなく、取引数が多いほどサンプルサイズが大きいということなのでデータとして信頼できるという意味で使用する必要があります。
OnTesterのソースコード(MQL5)
#include <Math\Stat\Math.mqh>
//+------------------------------------------------------------------+
//| 悲観的リターンレシオ(PRR)
//+------------------------------------------------------------------+
double OnTester()
{
const int dig = 2; // ←悲観的リターンレシオを小数点以下何桁まで表示するか
double PT = 0, LT = 0, PRR = 0;
//--- 勝トレード数と負トレード数
PT = TesterStatistics(STAT_PROFIT_TRADES);
LT = TesterStatistics(STAT_LOSS_TRADES);
//--- 悲観的リターンレシオの計算
PT = (PT - sqrt(PT)) * (TesterStatistics(STAT_GROSS_PROFIT) / PT);
LT = (LT + sqrt(LT)) * (-TesterStatistics(STAT_GROSS_LOSS) / LT);
PRR = PT / LT;
//--- 桁数の設定
PRR = MathRound(PRR, dig);
return PRR;
}上記のコードをEAに追加すれば悲観的リターンレシオをOnTester結果として出力することができます。MQL5用のコードですが、必要な方はコピペして使ってください。

◆GHPR
GHPRは各損益によって資産が平均で何%変動したかを示す指標です。複利運用でのGHPRが最大のシステムは、最も大きな利益額を出します。
HPR
先にHPRの説明をします。

GHPR
GHPRはHPRの幾何平均です。期待利得が複利運用のデータを正しく評価できなかったのに対して、GHPRは複利運用のデータを評価するのに適しています。GHPRが最も高いEAは複利運用において最大の利益を上げるものになります。

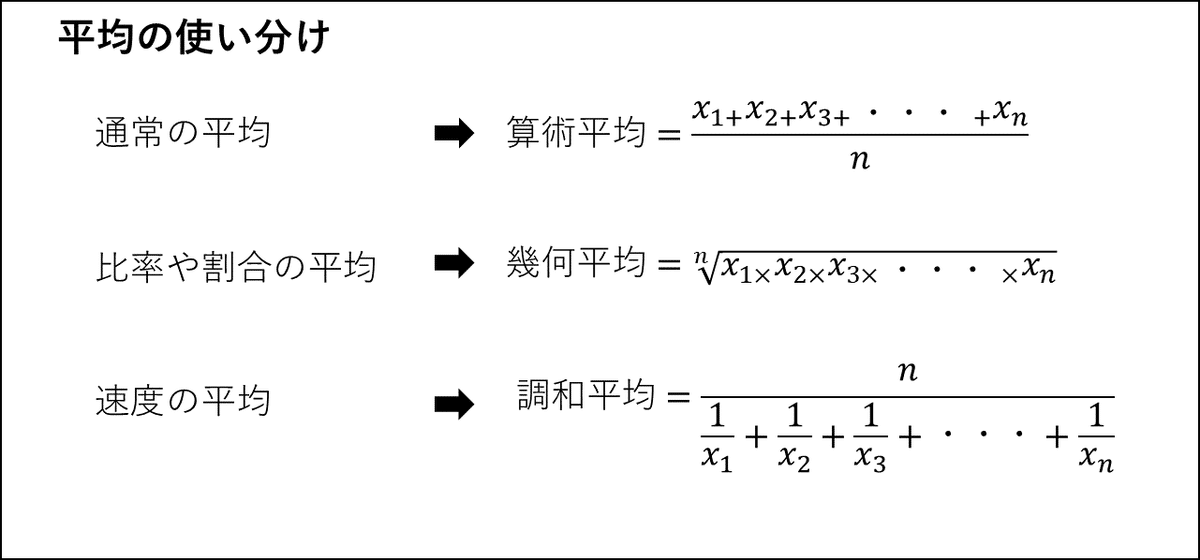
割合の平均値を求めるときには、一般的な平均の求め方である算術平均ではなく幾何平均を使います。
AHPR
HPRの算術平均です。各損益によって資産が平均で何%変動したかを知りたいときはGHPRを使います。AHPRはより別の計算の過程で使用したりするのでAHPR単体では見る必要はないかと思います。

◆最大ドローダウン(最大DD)
算出方法

他の評価指標は損益データをまとめたものであるのに対して、最大ドローダウンはひとつのバックテストデータでひとつだけサンプリングされるデータです。一部例外を除いてバックテスト結果の最大ドローダウンを将来発生するドローダウンの推測に役立てようとするのは間違いです。バックテストの最大ドローダウンを越えたらEAを停止するというルールをよく聞きますが、合理的なやり方ではないと思います。
最大ドローダウンの扱うときの注意点
注意点①単一バックテストの最大ドローダウンは無意味
EAが独立試行であるとすれば最大DDは「偶然に発生した損益の並び」がマイナスに偏ったことよってできた結果であるため、 単一バックテストの最大DDは取引回数(サンプルサイズ)にかかわらず、ほとんど意味のない数値といえます。
注意点②最大ドローダウン横軸とセットで扱う
最大ドローダウンは○○円 → ×
過去100取引での最大ドローダウンは○○円 → ○
バックテストの取引回数が1000回だったとします。リアルフォワード100回目の時点でバックテストの最大ドローダウンの80%くらいのドローダウンが発生しました。リアルフォワードの最大ドローダウンは大きすぎるのでしょうか?
このような疑問があってもバックテストの横軸(取引回数)とリアルフォワードの横軸(取引回数)がそろってないため比較することはできないのです。リアルフォワード100回目の時点での最大ドローダウンが大きいのか小さいのかを調べるためには、取引数100回のバックテストを複数用意してその平均と比較するなどの作業が必要です。最大ドローダウンの扱いがわからないと間違ったリスク管理につながると思います。
注意点③最大ドローダウンは複数個サンプリングして評価する


最大ドローダウンが1個だけでは評価の仕様がありません。横軸(サンプルサイズ)をそろえた最大ドローダウンを複数のサンプルから抽出して、その平均値や標準偏差(バラツキ)を評価するようにしましょう。
また、最大ドローダウンはモンテカルロ分析やスタートトレード分析を利用することで多数のサンプルから評価することもできます。
◆リカバリファクタ―(RF)
リカバリファクタ―は純損益を最大ドローダウンで割った値のことです。リターン÷リスクという形での評価指標となります。
リターン → 損益の合計(純損益)
リスク → 最大ドローダウン
リスクリターン率、リターンドローダウンレシオ、レストレーションファクターとも呼ばれます(呼び方がたくさんある)。
計算式


RFを扱うときの注意点
最大ドローダウンと同様に比較するときには横軸をそろえる必要があります。取引回数1000回のRFと取引回数100回のRFは比較できません。
EAの期待値がプラスであれば、RFは取引回数が増えていくほどに数値が増えていきます。これは純損益が取引を重ねるごとに増えるためです。多くのバックテスト指標は取引回数が増えるごとに値が収束するのに対して、RFは値の収束がないため、扱いが難しいものになっています。
リライアビリティファクター
リカバリファクタ―の扱いが難しいことをクリアするため、横軸を強制的にそろえた指標がリライアビリティファクターです。

リライアビリティファクターは横軸を1ヶ月という単位でそろえたものになります。横軸をそろえることが重要なので、必ずしも1ヶ月でなくてもいいのですが参考にはなるかと思います。
リカバリファクタ―をいくつかのリライアビリティファクターに分けることができます。複数のリライアビリティファクターの変化や傾向は、EAを評価するうえで重要な情報となる可能性があるかもしれません。
◆シャープレシオ(Sharpe ratio)
リカバリファクタ―が
リターン → 損益の合計
リスク → 最大ドローダウン
であったのに対して、シャープレシオは
リターン → 損益の平均
リスク → 損益のバラツキ
という形で「リターン÷リスク」を示す指標です。
計算式

FXのEA開発ではRFR=0として計算されることが多いです。通常は銀行の預金金利、または国庫債務の金利をRFRとして計算します。リスクがほとんどない利回りを考慮したい場合に計算に含めます。


シャープレシオは計算式を使い分けることで単利運用にも複利運用にも対応できる指標です。一般的にはシャープレシオが高いと損益が安定する、資産曲線がきれいな右肩上がりになると言われています。損益のバラツキがリスクになるという考え方はトレーダーにとって非常に重要なものだと思います。
シャープレシオ=1が意味するもの
損益データが正規分布となると仮定するとシャープレシオ=1は損益の平均(分析の頂点)と標準偏差の大きさが一致していることを意味しているため、標準的なバラツキでは損益はゼロを割らないことを意味しています。確率でいうと損益の84.135%が利益になります。

シャープレシオが定義するリターンは平均値であるため損益の中心を示しており、リスクはばらつきなので、シャープレシオが0よりも大きいほどに損失の割合が少なく安定したものであることを示しています。
「利益の割合、損失の割合って勝率のことじゃないの?」
と疑問に思うかもしれませんが、実際の損益データは正規分布になるとは限らないので勝率とは一致しません。
勝率は損益データを利益と損失の2つに分けるだけですが、シャープレシオは全体的に平均値の近くに損益がまとまっていればポジティブに、平均値から遠い値の損益が多ければネガティブに反応します。この性質により、シャープレシオは勝率よりも価値のある情報だと言えると思います。
◆ソルティノレシオ(Sortino ratio)
ソルティノレシオはシャープレシオをもとに考えられたもので、シャープレシオはリスクを「リターンのばらつき」としたのに対して、ソルティノレシオはリスクを下方リスク(損失方向のばらつき)に限定しています。「利益となる方向へのばらつきはリスクではないんじゃないか」と考えるとイメージしやすいと思います。

下方リスクについて
下方リスクの明確な定義は調べてもはっきりと見つからなかったのですが半偏差(Semi deviation)を下方リスクとする考え方もあるようなので、ここではこれを使ってソルティノレシオを計算していくことにします。

普通の標準偏差とは「平均値から各データがどれくらい離れているか」ということを示しているのに対して半偏差とは「平均より低いデータがそれぞれどれくらい離れているか」ということを示しています。
OnTesterのソースコード(MQL5)
#include <Math\Stat\Math.mqh>
//+------------------------------------------------------------------+
//| ソルティノレシオ
//+------------------------------------------------------------------+
double OnTester(void)
{
double sortinoRatio;
double plResults[];
double mean, semiDeviation;
//--- 取引損益を配列に書き込み
if(!GetTradeResults(plResults))
return 0;
//--- 取引損益の平均値を計算
mean = MathMean(plResults);
//--- 取引損益の半偏差を計算
semiDeviation = MathSemiDeviation(plResults);
//--- ソルティノレシオを計算
sortinoRatio = mean / semiDeviation;
sortinoRatio = MathRound(sortinoRatio,2);
return sortinoRatio;
}
//+------------------------------------------------------------------+
//| 取引損益を配列に書き込む
//+------------------------------------------------------------------+
bool GetTradeResults(double &plResults[])
{
//--- 全期間の取引履歴をリクエストする
if(!HistorySelect(0, TimeCurrent()))
return (false);
uint totalDeals = HistoryDealsTotal();
//--- 配列を、履歴の取引数にリサイズ
ArrayResize(plResults, totalDeals);
int counter = 0; // 取引回数カウンター
ulong ticketHistoryDeal = 0; // ディールチケット
//--- 全ての取引を配列に取得
for(uint i = 0; i < totalDeals; i++)
{
//--- 取引を選択する
if((ticketHistoryDeal = HistoryDealGetTicket(i)) > 0)
{
ENUM_DEAL_ENTRY dealEntry = (ENUM_DEAL_ENTRY)HistoryDealGetInteger(ticketHistoryDeal, DEAL_ENTRY);
long dealType = HistoryDealGetInteger(ticketHistoryDeal, DEAL_TYPE);
double dealProfit = HistoryDealGetDouble(ticketHistoryDeal, DEAL_PROFIT);
//--- 取引操作以外はスルー
if((dealType != DEAL_TYPE_BUY) && (dealType != DEAL_TYPE_SELL))
continue;
//--- エントリーアウトのみ
if(dealEntry != DEAL_ENTRY_IN)
{
//--- 取引結果を配列に書き込み、取引のカウントアップ
plResults[counter] = dealProfit;
counter++;
}
}
}
//--- 配列の最終サイズを設定する
ArrayResize(plResults, counter);
return (true);
}
//+------------------------------------------------------------------+
//| 半偏差
//+------------------------------------------------------------------+
double MathSemiDeviation(const double &array[])
{
int size = ArraySize(array);
double x = 0;
//--- 配列の要素数が1以下ならエラー
if(size <= 1)
return (double)"nan";
//--- 平均値を計算
double mean = 0.0;
for(int i = 0; i < size; i++)
mean += array[i];
mean = mean / size;
//--- 半偏差を計算
double semiDeviation = 0;
double counter = 0;
for(int i = 0; i < size; i++)
{
//--- 平均より低い値のみ計算
if(array[i] - mean < 0)
{
semiDeviation += pow(array[i] - mean, 2);
counter++;
}
}
return MathSqrt(semiDeviation / (counter - x));
}上記のコードをEAに追加すればソルティノレシオをOnTester結果として出力することができます。MQL5用のコードですが、必要な方はコピペして使ってください。

◆回帰分析による決定係数(R2)
計算式

決定係数は 0 ~ 1 の数値となり、データが近似線に近いほど(まっすぐなデータであるほど)1に近づき、近似線からばらついているほど0に近づくものです。バックテストの損益データに適応することでEAの安定度合いを示す可能性があります。
OnTesterのソースコード(MQL5)
//+------------------------------------------------------------------+
//| 決定係数 R2
//+------------------------------------------------------------------+
double OnTester(void)
{
double R2;
double profit_results[];
double RSS, TSS;
//--- 取引損益を配列に書き込み
if(!GetTradeResults(profit_results))
return 0;
//--- 残差平方和
RSS = MathRSS(profit_results);
//--- 全体平方和
TSS = MathTSS(profit_results);
//--- 決定係数
R2 = 1 - (RSS / TSS);
return R2;
}
//+------------------------------------------------------------------+
//| 取引損益を配列に書き込む
//+------------------------------------------------------------------+
bool GetTradeResults(double &plResults[])
{
//--- 全期間の取引履歴をリクエストする
if(!HistorySelect(0, TimeCurrent()))
return (false);
uint totalDeals = HistoryDealsTotal();
//--- 配列を、履歴の取引数にリサイズ
ArrayResize(plResults, totalDeals);
int counter = 0; // 取引回数カウンター
ulong ticketHistoryDeal = 0; // ディールチケット
//--- 全ての取引を配列に取得
for(uint i = 0; i < totalDeals; i++)
{
//--- 取引を選択する
if((ticketHistoryDeal = HistoryDealGetTicket(i)) > 0)
{
ENUM_DEAL_ENTRY dealEntry = (ENUM_DEAL_ENTRY)HistoryDealGetInteger(ticketHistoryDeal, DEAL_ENTRY);
long dealType = HistoryDealGetInteger(ticketHistoryDeal, DEAL_TYPE);
double dealProfit = HistoryDealGetDouble(ticketHistoryDeal, DEAL_PROFIT);
//--- 取引操作以外はスルー
if((dealType != DEAL_TYPE_BUY) && (dealType != DEAL_TYPE_SELL))
continue;
//--- エントリーアウトのみ
if(dealEntry != DEAL_ENTRY_IN)
{
//--- 取引結果を配列に書き込み、取引のカウントアップ
plResults[counter] = dealProfit;
counter++;
}
}
}
//--- 配列の最終サイズを設定する
ArrayResize(plResults, counter);
return (true);
}
//+------------------------------------------------------------------+
//| 残差平方和 RSS
//+------------------------------------------------------------------+
double MathRSS(const double &change[])
{
//--- データが十分か確認する
if(ArraySize(change) < 3)
return (double)"nan";
int n = ArraySize(change);
double a_coef, b_coef;
double reg[];
ArrayResize( reg, n);
//--- 線形回帰を計算する
double x = 0, y = 0, x2 = 0, xy = 0;
for(int i = 0; i < n; i++)
{
x = x + i;
y = y + change[i];
xy = xy + i * change[i];
x2 = x2 + i * i;
}
//--- 傾きと切片
a_coef = (n * xy - x * y) / (n * x2 - x * x);
b_coef = (y - a_coef * x) / n;
//--- 残差平方和 RSS
double RSS = 0;
for(int i = 0; i < n; i++)
{
//--- 回帰直線
reg[i] = b_coef + a_coef * i;
//--- 残差二乗
RSS += MathPow(change[i] - reg[i], 2);
}
return RSS;
}
//+------------------------------------------------------------------+
//| 全体平方和 TSS
//+------------------------------------------------------------------+
double MathTSS(const double &array[])
{
int size = ArraySize(array);
double x = 0;
// 配列の要素数が2以下ならエラー
if(size < 2)
return (double)"nan";
// 平均値を計算
double mean = 0.0;
for(int i = 0; i < size; i++)
mean += array[i];
mean = mean / size;
// 全体平方和を計算
double TSS = 0;
for(int i = 0; i < size; i++)
TSS += MathPow(array[i] - mean, 2);
return TSS;
}