見出し画像

BM25 のパラメタをいじって Hybrid search を固有名詞に強くする

AIcia Solid Project

Atrae Advent calendar 2024 3日目！
 Virtual Data Scientist のアイシア=ソリッドです。
もうさっそく本題行きましょう！

背景 : LLM 活用の本質は検索

大生成 AI 時代、誰も彼もが LLM の活用を模索していますよね。LLM 活用の本質は検索にあります。RAG が流行っていることから分かるように、LLM に与える prompt に適切な情報を入力すれば、LLM の出力の品質を高めることができます。この情報の選択は、広くいえば検索そのものです。なので、検索の良し悪しが LLM 活用の良し悪しを決定する重大な因子の1つとなります。
（実は GPT-3 の論文タイトルは、"Language Models are Few-Shot Learners" であり、まさにその事を言っていたりします。）

検索といえば、最近流行りの vector search (semantic search) と、古くからある ES 等の全文検索が2大巨頭です。
vector search はいい感じに意味を捉えて検索できますが固有名詞に弱く、
全文検索は固有名詞には強くても意味をうまく捉えられない傾向があります。
なので混ぜよう！　という話になり、vector search のスコアと全文検索のスコアを合成して検索する hybrid search が流行っております。

Hybrid search の文脈でなぜかよく使われる全文検索のアルゴリズム BM25 には、 $${k_1}$$ と $${b}$$ というパラメタがあります。これらはそれぞれ、複数回登場時のバフ制御・長文に対するペナルティの意味合いを持ちます。これを文脈に応じて調整すると、よき hybrid search を素早く作れます。

これは、ChatGPT が出て以降初の改修だった、Green の（ログイン後の）検索に利用されています。参考にどうぞ！

BM25 の復習とパラメタ設定

というわけで、BM25の復習をしましょう。BM25は、検索クエリ $${q}$$ と文章 $${d}$$ に対して、以下の関数でスコアを計算し、そのスコアの降順で検索結果を提示するアルゴリズムです。

$$
\text{score} (q, d) = \text{idf}(q) \times \frac{(k_1 + 1)f(q, d)}{f(q, d) + k_1 \left(1 - b + \frac{\#d}{avgdl} \right)}
$$

（なお、ここでは、簡単のため、検索クエリは1単語 $${q}$$ のみが入力されたとします）

ほぼ同じ内容をこの動画で解説しているので、動画のほうが好きな方はこちらからご覧ください！

$${k_1}$$ について

この数式に登場する $${avgdl}$$ は、検索対象文書の平均単語数であり、$${#d}$$ は検索対象の文書 $${d}$$ の単語数です。そのため分数の右下に出てくる $${\frac{\#d}{avgdl}}$$ は、文章 $${d}$$ の単語数の相対的な大きさを表します。ここに $${b}$$ が登場しており、この $${b}$$ が長文に対するペナルティを支配しています。
ですが、先にこれを考えると難しいので、まずは $${\#d = avgdl}$$ の場合を考えましょう。
このときは、スコア関数 $${\text{score} (q, d)}$$ は以下の式に変形できます。

$$
\text{score} (q, d) = \text{idf}(q) \times \frac{(k_1 + 1)f(q, d)}{f(q, d) + k_1 }
$$

まずはこの数式の意味を見ていきましょう。この中に登場する $${f(q, d)}$$ は、単語 $${q}$$ が文書 $${d}$$ に登場する頻度を表す関数です。
実は、この実装様々なバリエーションがあるのですが、今回は最も標準的な、単語 $${q}$$ の登場回数を表すとしましょう。

$$
f(q, d) = \text{(単語 } q \text{ のテキスト } d \text{ 内の登場回数)}
$$

これを $${x = f(q, d)}$$ とかくと、$${\text{score} (q, d)}$$ と $${x = f(q, d)}$$ の関係を、様々 $${k_1}$$ の値で描画すると、以下の図が得られます。

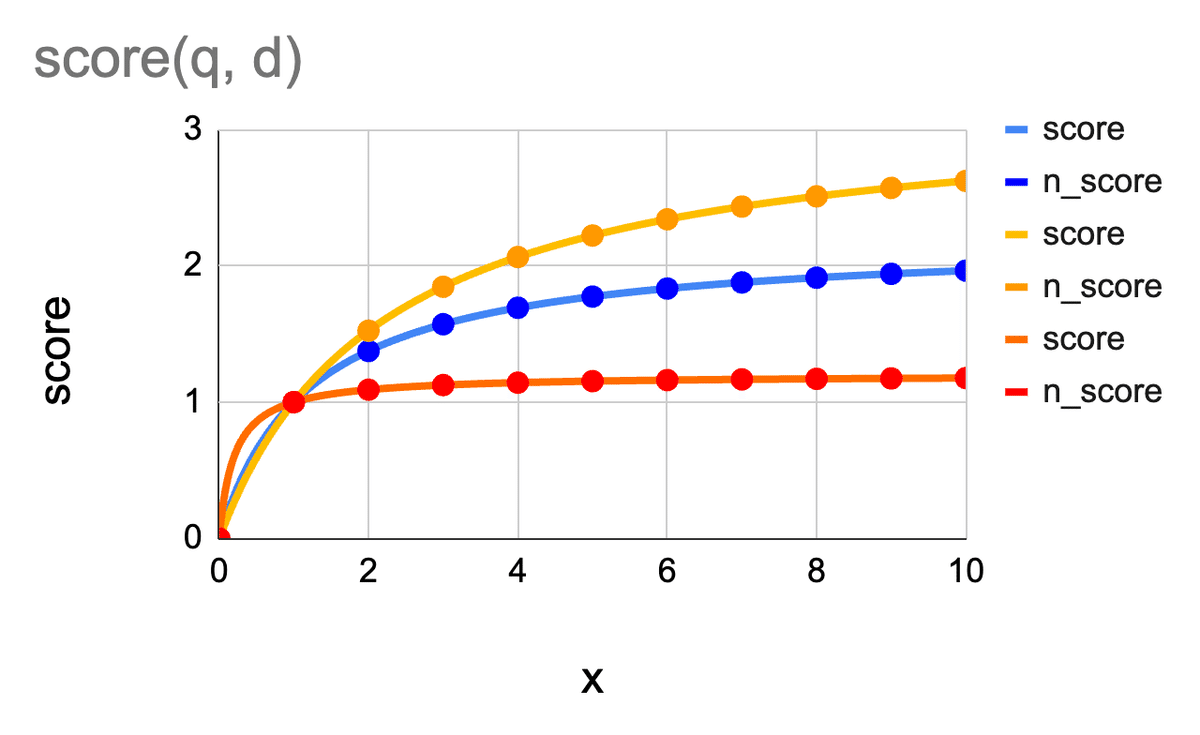
この図では、$${\text{idf}(q) = 1}$$ の場合です。idf の議論は今回の本質ではないので、以降も $${\text{idf}(q) = 1}$$ とします。

上図では、青がデフォルト値の $${k_1 = 1.2}$$、黄色が少し大きい $${k_1 = 2.2}$$、赤が少し小さい $${k_1 = 0.2}$$ の場合のグラグです。

どの場合も、単語の登場回数が増えるにつれて、score が高くなることが分かります。

更に良く見ると、$${k_1}$$ の値が何であれ、$${x = 1}$$ のときのスコアは1であり、$${k_1}$$ が大きいほど、$${x > 1}$$ でのスコアが大きくなっています。そのため、$${k_1}$$ が小さければ小さいほど、「1回登場」と「2回以上登場」の差がなくなります。これが超重要です！

全文検索の性能を上げるためであれば、ある程度の大きさの $${k_1}$$ を設定して、複数回登場する単語の重みを高める必要があります。（たくさん登場する単語は、文意との関係が深いと思われるため）
一方、固有名詞に引っ掛けるために全文検索を利用する場合、1回登場も2回以上の登場も大差ありません。なので、この hybrid search での固有名詞対策なら、 $${k_1}$$ を小さいことが望ましいでしょう。

$${b}$$ について

次は、$${b}$$ について見てみましょう。$${\frac{\#d}{avgdl} = 5}$$ の場合、つまり、文章 $${d}$$ がかなり長い場合の score の様子です。

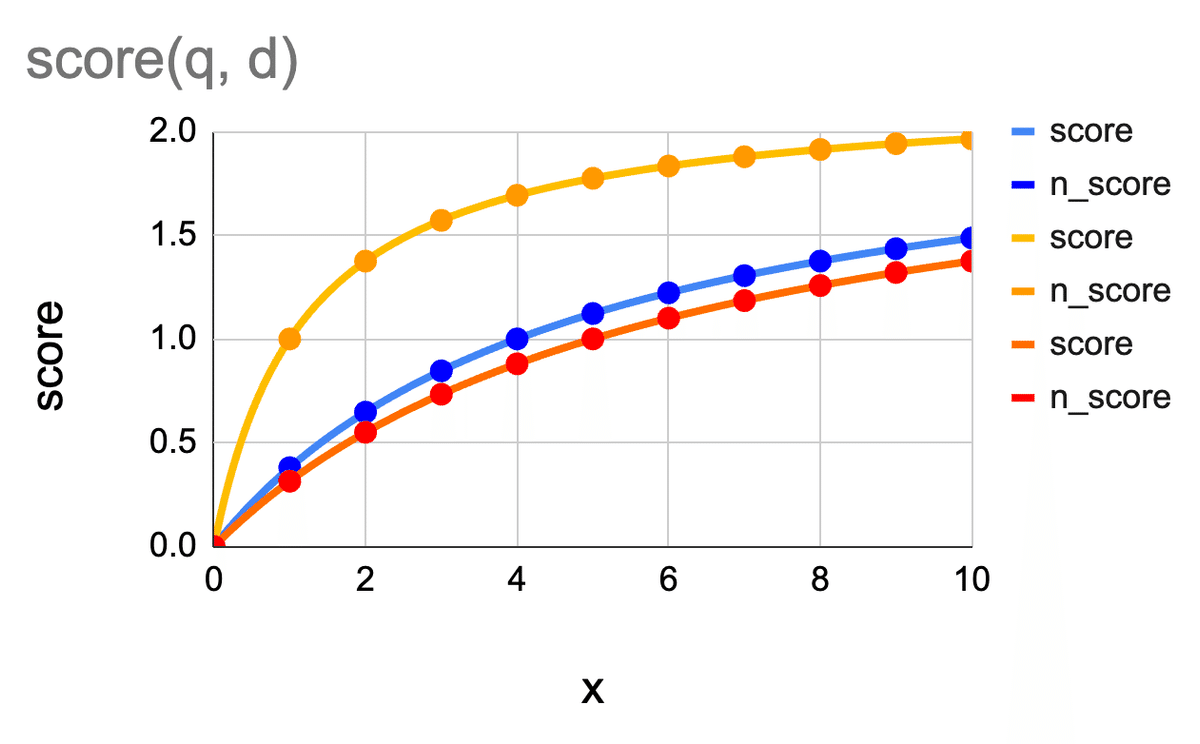
今度も、青がデフォルトの $${b = 0.75}$$ で、黄色は $${b = 0}$$、青が $${b = 1}$$ の場合です。（$${b}$$ は 0~1 で設定されるパラメタです）

見ての通り、$${b}$$ の値が大きいほど、スコアが小さくなっています。つまり、$${b}$$ の値が大きいほど、文章が長い罰を強く食らうことになります。

まぁ $${b}$$ はだいたいデフォルトのまま動かさなくても問題ないですが、例えば、本来短いべきテキスト（タイトルなど）にキーワードたくさん詰め込んで引っかかりやすくする工夫を、プラットフォームとして好まない場合、$${b}$$ を標準より大きめに設定すれば、そういうアイテムが検索上位から消えることになります。
逆に、キーワードをたくさん詰め込んだほうがわかりやすいと判断する場合は、$${b = 0}$$ と設定して、長さの罰則をゼロにするのもよいでしょう。

まとめ

というわけで、hybrid search にて固有名詞を引っ掛けるために BM25 を使う場合

  • $${k_1}$$ は小さめ推奨

  • テキストが長いことに罰則を入れたい場合（キーワード詰め込みに罰則を入れたい場合等）は、$${b}$$ は大きめに（デフォルトの $${b = 0.75}$$ でも OK）

  • テキストの長さの罰則をゼロにするなら、$${b = 0}$$ に

宣伝

というわけで、こんな感じで、数式の意味を読み取り、数式の領域で創造性を発揮できる人が、じわじわ活躍している会社だったりします。
てか私がいるよ！
興味ある人は来てね！

そんなことより！　私こんな感じで数学とか数理統計っぽい技を使いながら仕事してます。で、数理統計の成果を今年のバーチャル学会で発表するので、よかったら見に来てね！

あと、せっかくなので、チャンネル登録よろしく！

じゃ、またね！


いいなと思ったら応援しよう！