統計学: 統計的推定と必要な標本数の決定(二項分布の場合)
前記事から続けて、二項分布で考えてみましょう。二項分布で出てくる確率pは母比率と呼ばれます。母比率pをデータから統計的に推定することを考えましょう。必要な精度の話をしたいので、区間推定を想定します。成功確率がpである試行をn回行うときに成功する回数をkとすると、前記事の通りkは二項分布

に従います。
二項分布のkの期待値E(k)と分散V(k)はそれぞれ


となることを思い出しましょう。ここで、古典統計学で最も重要な、そして魔法のような定理である「中心極限定理」が登場します。nがある程度大きいとき、二項分布は平均np、分散np(1-p)の正規分布で近似できます。
これが中心極限定理から出てくる結論の例になっています。

これにより、kが二項分布に従う場合、kを標準化して

を定義すると、zはnが十分に大きいときには標準正規分布に従います。
標本比率は直感の通り

から求められます。少し面倒な計算をすると、zは

と書けるので、これもnが十分大きいとき標準正規分布に従います。この統計量zが標準正規分布に従うことを利用すれば、zの信頼区間を計算できます。
標準正規分布の95%信頼区間は[-1.96, 1.96]であることから、

となるので、変形すれば
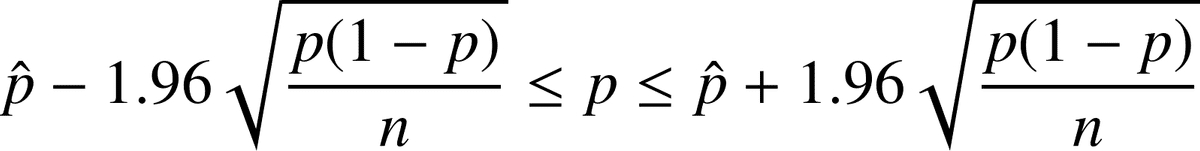
となります。
これで母比率についての95%信頼区間を算出するための式が得られた…ように見えます。しかし、信頼区間の上限値と下限値には母比率pが含まれたままなので、信頼区間を計算できません。このため、pを推定値(標本比率)
で置き換えることで

が得られ、手持ちのデータから求められる形の区間推定となります。

この式より、95%信頼区間の幅は

と書けます。
この式を使うと、必要な推定精度(つまり信頼区間の幅)を設定した時の必要なサンプルサイズを算出できます。必要な精度をαとすると、標本比率も推定できているので

です。よって最低限必要な標本数nは

によって求められます。
たとえば標本比率= 0.1、α = 0.05のときはn ≥ 553.2となり、n = 554以上あればよいことが分かります。この記事では95%信頼区間を用いましたが、これも任意の値に一般化できます。また場合によっては母比率の推定が与えられないこともありますが、その場合はp = 0.5を代入してnを求めれば、必要な標本数は確保できます。
この式から、nが大きくなると信頼区間の幅は狭くなり、より正確な推定ができるという「常識」も定量的に示せたことになっています。
付録
上では確率変数Xとその実現値kを区別せず、実現値のみで表現しています。このままでは数学的に不正確なので、以下ではもう少し厳密に表現してみます。また計算も補完しておきます。
二項分布に従う確率変数Xの期待値と分散は、


となります。上の簡易版と違うのは、Xは確率変数、つまり確率的にある値を取る関数であるということで、これがkという実現値を取ったときはX=kと表現します。計算上不要に見えるかもしれませんが、現代の公理論的確率論の基礎のところでは大切になります。
確率変数Xを上記の期待値(平均)と分散を用いて正規化し、新しい確率変数Zを
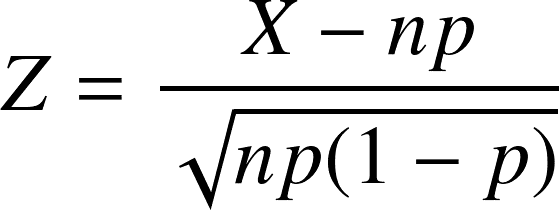
と定義します。上で見たように、Zは標準正規分布に従います。これを、母比率の推定値

を用いてさらに変形してみます。

このようにして、本文での式が得られます。
(2024年2月15日 初稿)
