統計学: 0か1かの話(二項分布入門)
昨今の世相を反映してか、0か1か、あるいは0か100かという議論(往々にして口論)をよく目にするようになりました。ここでは0か1かに規格化して話をしますが、白か黒か、正か負かでも基本的に同じ話です。
細かいことを考えないと、0か1かと言われたらどちらも同様に確からしいと思いがちな人が多いようです。しかし、こういう2者択一の問題には、ひとつ明示的になっていない重要な数値が隠れています。それが2つの選択肢の生じる確率で、0か1かと言った時点では50-50だとは誰も言っていないわけです。
少し定量的に表現するため、ここでは1が生じる確率をpとします. 確率なので規格化されていて、0 ≤ p ≤ 1です。よくある例として1を成功、0を失敗とする試行を考えると、成功率が極めて低い事柄は世の中いくらでもあります(宝くじ1等当選など)。つまり、pがどのくらいかを考えに入れなければ定量的なことは言えません。
標本数(あるいは試行回数)をnと置き、このうち1が生じた回数をkとします。この状況が実現する確率は

となります。!はn!, k!といちいち数字に驚いているのではなく、階乗

を意味します。物々しい分数の係数は二項係数と呼ばれ、

と書かれることもあります。よく見ると、p^k は k 回1となる確率を表し、(1 − p)^(n−k) は n − k 回0となる確率を表しています。Wikipediaからグラフを借りてきましょう。
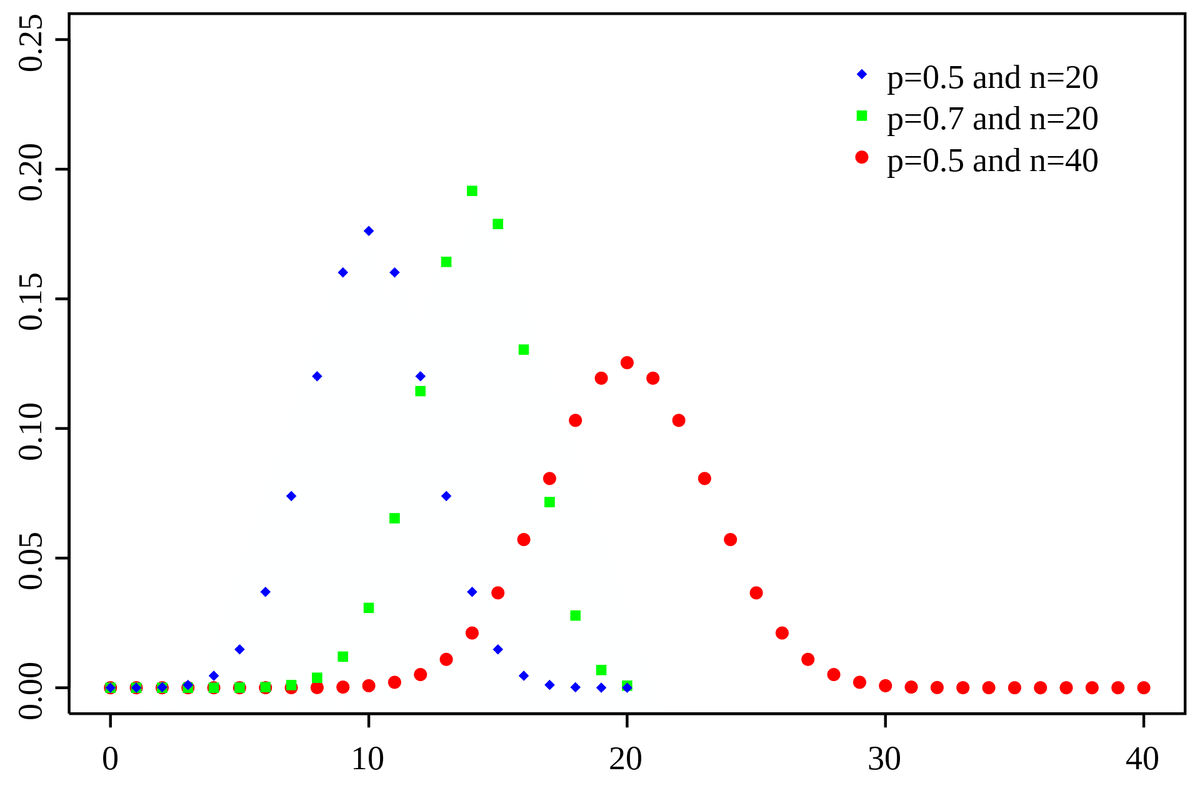
式で書いてはみたものの、これだけでは直感と結びつきにくいでしょう。実現値kの平均はどのくらいでしょうか? ちょっと面倒な計算をすると、kの平均はnpであることが導けます。確率がpの事象がn回ある(あるいはn回試行する)ので、納得の結果です。
そして統計で同じくらい大事なのが、実現値は平均の周りにどのくらい散らばるのかを表す分散という量です。あるいはその平方根である標準偏差のほうが使いやすいかもしれません。同じく少し計算すると、分散はnp(1-p)となることが分かります。
平均、分散(標準偏差)とも、生起確率pが入っています。つまり、当然ながら0か1かの実現は1が生じる確率pに明示的に依るわけです。ところが、pが最初から分かっていることは極めて稀で、現実のデータを吟味する必要があります。そしてpは1回の観測では分かりません。統計的な推測のためには標本数nが大切であるという事実がここで出てきます。
標本数nがどのくらいあれば信頼に足る統計的結論が得られるのかについては稿を改めますが、どのくらいの精度の結論が必要かで決まります。この信頼性が大切で、そこを設定せずにnが多いだ少ないだと述べている言説は全部不毛なのです。
特にオチらしい結論はありませんが、理解の足しになれば幸いです。
(初稿: 2024年2月11日)
