花束を沢山作る方法
本記事はAcompany5周年アドベントカレンダーの10日目の記事となります。
はじめに
この記事は日本の競技プログラミングの大手サイト AtCoder の花束と言う問題の解説記事になります。
メインの対象読者は AtCoder を既にプレイしている人ではなく、競技プログラミングとは何かをイマイチよく知らない人です。
具体的な問題に触れることを通して競技プログラミングの概観を少しでも掴んでもらえたら嬉しいです。
競技プログラミングとは?
与えられた課題を解くプログラムを提出する競技です。
「こんな機能のついた電卓を作ってください」みたいなイメージです。
と言ってもよく分からないと思うので、早速例題の花束に進みましょう。
花束
問題リンク
※ 問題の内容は適宜テキストや画像で説明しますが、上のリンクから先に一読しておいた方が分かりやすいかもしれません。
問題文
高橋君は赤い花を $${{ R }}$$ 本、青い花を $${{ B }}$$ 本持っています。高橋君は次の $${{ 2 }}$$ 種類の花束を作ることができます。
$${{ x }}$$ 本の赤い花と $${{ 1 }}$$ 本の青い花からなる花束
$${{ 1 }}$$ 本の赤い花と $${{ y }}$$ 本の青い花からなる花束
高橋君が作ることのできる花束の個数の最大値を求めてください。すべての花を使い切る必要はありません。
まず最初に今回プログラムを用いて解決したい課題が与えられます。
今回は「2色の花の本数」と「花束の色の構成比」を入力したら「作れる花束の個数」を表示するプログラムを作れば ok です。
問題文を読んでも言ってる意味がよく分からないと言う方は、この後の要件を一度飛ばして先に入出力例の項を見るとイメージが湧くかもしれません。
ちなみに文中の「高橋君」はAcompany社長の高橋亮祐さんのことではなく、AtCoder社長の高橋直大さんのことです。
要件
制約
$${{ 1\leq R,B \leq 10^{18} }}$$
$${{ 2\leq x,y \leq 10^{9} }}$$
入力
$${{ R \space B }}$$
$${{ x \space y }}$$
出力
高橋君が作ることのできる花束の個数の最大値を出力せよ。
実行時間制限
2秒
次に課題の具体的な要件が与えられます。
制約では花の本数として $${{ 1 }}$$ 以上 $${{ 10^{18} }}$$ (100京!!)以下のどんな整数が与えられても正しく動くことなどが要求されています。
入力では今回入力される数の与えられる形式などが指定されています。
「2色の花の本数」を空白区切りで入力し、改行を挟んで「花束の色の構成比」を空白区切りで入力した時に答えを出力することが要求されています。
実行時間制限では入力したら2秒以内にプログラムの実行が終わることが要求されています。
入出力例
入力
$${{ 10 \space 8 }}$$
$${{ 3 \space 2 }}$$
赤い花10本と青い花8本に対して花束の作り方が「赤3本+青1本」と「赤1本+青2本」の二通りある際、花束は最大で何個作れますか?と言うことです。

例えば以下のようにすると4つの花束が作れます。

あるいは以下のような作り方でも4つの花束が作れますね。

実は、以下のようにすれば5つの花束が作れます。
証明はしませんが、今回 6つ以上の花束を作ることは出来ないため、この入力に対して期待されるプログラムの出力は5と言うことになります。

$${{ 10 \space 8 }}$$
$${{ 3 \space 2 }}$$
と入力したら 5 を表示するだけでなく、その他制約内のどんな4つの値が入力されても、その状況に応じた花束の最大個数を表示すると言うのが、この問題で要求されてるプログラムの要件になります。
問題設定については理解いただけたでしょうか?
以下では実際に Python と言う言語で書かれたプログラムを見せながら、この問題の解説を行います。(AtCoder では Python 以外にもさまざまな言語が対応しており、好きな言語でプレイすることが出来ます)
プログラムはなるべく分かりやすく書くつもりですが、全て理解する必要はありません。
プログラム内に # が登場した場合、その行の # 以降の文字(note がそのコードを Python と認識していれば薄くなっていると思います)はコメントアウトと言って読み手のために書かれたプログラムの説明になります。
コメントアウトはプログラムの実行結果には影響を与えないことをここで注意しておきます。
採点方法
解説に入る前に、プログラムが正しいかどのようにチェックするか気になった人がいるかもしれないので、プログラムの採点方法について簡単に記述しておきます。
プログラムを提出するとテストケースと呼ばれる、大体50~100個程度の入力(それぞれの具体的な数値は提出者からは分からない)が AtCoder 上で自動でプログラムに入力されます。(テストケースの個数は問題によります)
例えば先ほどの例を入力したら 5 を返すかなどのように、用意されている全てのテストケースに対して正しい答えを出力することが確認出来たら正解になります。
もちろん要件的にはありうる入力と言うのは100個どころではありません。
ですが AtCoder ではトッププレイヤー達が「正しく無いプログラムなら大体このどれかのケースで間違った答えを出す」ようにテストケースを作成しているため、間違ったプログラムが用意されたテストケースに対し全部正しい答えを返すことはほとんどありません。(そう言ったプログラムはしばしば嘘解法と呼ばれ、全く無いと言うことはないのですが…)
この方法によって AtCoder をプレイする人間は24時間365日、どんな時間にプログラムを提出しても数秒から数十秒で自分の作ったプログラムが正しいか判定してもらえるのです。
解説
花束の解説です。
この記事の読者の多くはプログラミングの経験は無いけど数学の問題を解いた経験はある状態だと思います。
僕も最初はそうだったのですが、数学の考え方が頭に染み付いていると、この問題を解こうとした時 $${{R,B,x,y}}$$ を使った綺麗な式で答えを表すことを真っ先に考えると思います。
実際、もし作れる花束が「赤$${{x}}$$本+青$${{1}}$$本」と「赤$${{1}}$$本+青$${{y}}$$本」ではなく「赤$${{ x }}$$本」と「青$${{y}}$$本」であったならば、答えは $${{ \lfloor \dfrac{R}{x} \rfloor + \lfloor \dfrac{B}{y} \rfloor }}$$ と綺麗な形で書くことが出来ます。( $${{ \lfloor a \rfloor }}$$ は $${{ a }}$$ の整数部分を表します。例えば $${{\lfloor 3.2 \rfloor=3}}$$, $${{\lfloor 1.0 \rfloor=1}}$$ です)
このように作りたいのが一色の花束の場合であれば、以下のようなプログラムで正解することが出来ます。
# 入力を受け取る
R, B = map(int, input().split())
x, y = map(int, input().split())
# R/x と B/y の整数部分の和を出力
print( R//x + B//y )一方で今回の問題では、上のような綺麗な式はおそらく簡単には見つからないと思います。
実際、この問題を解く上で綺麗な式を見つける必要はありません。
なぜならプログラムは実行中に沢山の計算や条件分岐を行うことが出来るからです。
例えば、以下のコードは「赤$${{x}}$$本+青$${{1}}$$本」の花束の個数と「赤$${{1}}$$本+青$${{y}}$$本」の花束の個数としてあり得そうなものを全部試してみると言うコードです。
一点プログラムを読む上での注意なのですが、プログラム中で a = 1 のように = で左右を結んでいる場合「a と 1 が等しい」と言う意味ではなく「a を 1 とする」と言う意味になります(代入操作)。
a = 1 の後に a = a + 1 と書いた場合、a を 1 としたのち、a を a+1 で置き換えるので、最終的に a が 2 になると言うことです。
これは少し難しい概念だと思うので、ここでは完璧に理解する必要はありません。
# 入力を受け取る
R, B = map(int, input().split())
x, y = map(int, input().split())
# 暫定解を 0 にしておく
answer = 0
# 赤x + 青1 の花束の個数は高々B以下なので、0以上B+1未満の数を全部試す
for hanataba1 in range( B + 1 ):
# 赤1 + 青y の花束の個数は高々R以下なので、0以上R+1未満の数を全部試す
for hanataba2 in range( R + 1 ):
# それぞれの色について今いくつ花を使おうとしているかを計算
red = hanataba1 * x + hanataba2
blue = hanataba2 * y + hanataba1
# それぞれの色について花が足りる場合
if red <= R and blue <= B:
# 暫定解を今までの暫定解と今回の花束の個数の大きい方に更新する
answer = max( answer, hanataba1 + hanataba2)
print( answer )こちらからこのプログラムが先ほどの入力例に5を返すことが確認出来ます。
また、リンク先のコピーして編集を押すことで編集が出来るようになります。
標準入力の欄の数を好きな数に書き換えて実行を押してみることで、さまざまな入力に対して正しい答えを返すことが確認できると思います。(正しいかどうかを確かめるのは難しいですが…)
全角数字などを入れるとうまく動かないので注意してください。
ではこのコードを提出すればこの問題は正解を貰えるのかと言うと、実がそうではありません。
あくまで上のコードはプログラムは実行中に沢山の計算や条件分岐を行うことが出来ることの例示でしかなく、これは競技プログラミングをプレイする上での大前提あり、この土俵の上でプレイヤーは鮮やかなロジックを日々模索しています。
以下では実際にプレイヤーが問題を解くためにどのような工夫を行っているのかについて解説します。
まず先ほどのコードがどうして正解にならないかについて先に説明しておきましょう。
$${{R,B,x,y}}$$ として $${{10^{18},10^{18},2,2}}$$ が入力された時を考えてみます。
先ほどのコードは二種類の花束についてそれぞれ $${{0}}$$~$${{B}}$$, $${{0}}$$~$${{R}}$$ 通りを全て試していたので、この場合約 $${{ 10^{18}\times 10^{18} = 10^{36} }}$$ 通りを全て試すことになります。
一般のコンピュータが一秒間に行える計算は大体 $${{10^8}}$$~$${{ 10^{10} }}$$ 回です。(一億〜百億回程度)
したがって、$${{10^{36}}}$$ 通りを全て試すには少なくとも$${{ 10^{26} }}$$ 秒くらいはかかりそうだと言うことが分かります。(300𥝱年くらい(𥝱 は 億を二回かけた値です))
したがって、この問題は $${{10^{18},10^{18},2,2}}$$ が入力された場合でも実行時間制限の2秒以内に答えを返すことが要求されているため、上のコードでは間違いになります。
ではどのようにすれば2秒以内、言い換えれば高々 $${{10^9}}$$ 回程度の計算で正しい答えを出せるのでしょうか?
二つの Step に分けて解説します。
Step1 判定問題を解く
花束の最大個数を求めるのは難しいので、もう少し簡単な「花束を $${{ k }}$$ 個作れるか?」と言う判定問題を考えてみることにします。
例えば最初に挙げた例のように $${{R,B,x,y}}$$ がそれぞれ $${{10,8,3,2}}$$ の時に「花束を4個作れるか?」や「花束を6個作れるか?」と言う問題なら簡単に解けるだろうかと言うことです。
花束を
「赤$${{x}}$$本+青$${{1}}$$本」「赤$${{1}}$$本+青$${{y}}$$本」
ではなく
「(赤$${{1}}$$本+青$${{1}}$$本)+(赤$${{x-1}}$$本)」「(赤$${{1}}$$本+青$${{1}}$$本)+(青$${{y-1}}$$本)」
と言い換えてみます。
こうすることで問題を
どちらの種類の花束でも一個作ろうとしたら赤$${{1}}$$本+青$${{1}}$$本を消費する
さらに赤$${{x-1}}$$本か青$${{y-1}}$$本のどちらかを消費する
と見ることが出来るようになります。
したがって「花束を$${{k}}$$個作れるか」と言う問いは、赤と青を$${{k}}$$本消費した上で、赤$${{x-1}}$$本か青$${{y-1}}$$本を合計$${{k}}$$個取れるかと言う問題を解けばいいことが分かります。
序盤に述べたように一色の花束に関しては簡単な割り算で作れる個数の最大値が求められるので、この問題は下のコードで解くことが出来ます。
# 入力を受け取る
R, B = map(int, input().split())
x, y = map(int, input().split())
# 赤R-k本と青B-k本から赤x-1本と青y-1本を取れる個数の最大値は (R-k)//(x-1) + (B-k)//(y-1)
# これが k 以上ならば k 個作れる
if (R-k)//(x-1) + (B-k)//(y-1) >= k:
print("k 個作れる")
else:
print("k 個作れない")こちらから上のコードを試すことが出来ます。
リンク先では $${{R,B,x,y}}$$ が $${{10,8,3,2}}$$ の際に $${{k}}$$ 個作れるか?を $${{k=4}}$$ として判定しています。
再びコピーして編集を押してコード内の $${{k=4}}$$ の箇所を $${{k=6}}$$ などに変更してみると判定結果が変わることが確認できると思います。
Step2 二分探索する
Step1 で $${{k}}$$ 個作れるか?と言う判定問題は簡単に解けることが確認出来ましたが、最大何個作れるか?と言う問題は結局どのように解けばいいのでしょうか。
作れる花束の個数が$${{10^{18}}}$$個未満であることはあらかじめ分かっていますが、ここで $${{1}}$$個作れるか、$${{2}}$$個作れるかと言う感じで$${{10^{18}}}$$個作れるかまでを一個ずつ全て確かめようとしたら $${{10^{8}}}$$ 秒ほどかかってしまいます。
では下から順繰りに聞いていくのではなく最初に $${{100}}$$ 個作れるかを確かめてみるのはどうでしょうか。
もし作れないのであれば、答えの候補は一気に$${{0}}$$から$${{99}}$$までの$${{100}}$$通りに絞ることが出来ます。
$${{100}}$$個作れるのであればまだ答えの候補は$${{100}}$$から$${{10^{18}-1}}$$の間であまり絞れていませんが、それでも一回の質問で$${{100}}$$個も候補を減らすことが出来ました。
この考え方をもう少し進めてみましょう。
$${{100}}$$個作れるかを確かめてみる作戦の良くない部分は、その可否によって答えの候補の絞り具合に大きな差があることです。
最初に($${{0}}$$と$${{10^{18}}}$$の真ん中の)$${{5\times 10^{17}}}$$個作れるかを確かめることにします。
作れないなら答えの候補は$${{0}}$$から$${{5\times 10^{17}-1}}$$になり、作れるなら答えの候補は$${{5\times 10^{17}}}$$から$${{10^{18}-1}}$$になるので、どちらの場合も答えの候補を元の半分に減らすことが出来ます。
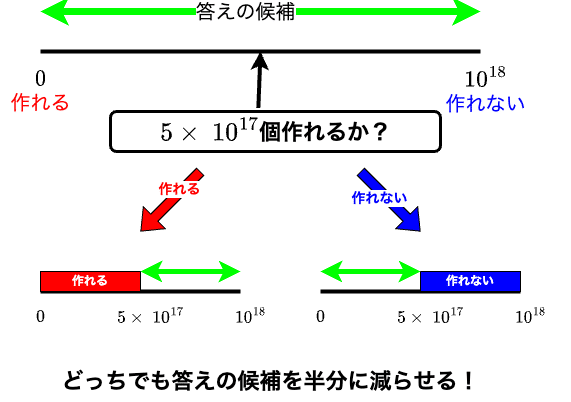
このように答えの候補区間の真ん中に対して「$${{k}}$$個作れるか」を確かめることを繰り返すことで、候補を半分半分にしていくことが出来ます。
$${{10^{18}}}$$ は $${{60}}$$ 回半分にすると$${{1}}$$以下になるので、この問題は高々$${{60}}$$回判定問題を解くことで答えの候補を1通りに絞れることが分かりました。
競技では以上のロジックを制限時間内に思いつき、それをコードに落とし込む必要があります。
# 入力を受け取る
R, B = map(int, input().split())
x, y = map(int, input().split())
# 0個は確実に作れる, 10^{18}個は確実に作れない
ok = 0
ng = 10**18
# ok + 1 が ng になった時の ok が答え
while ok + 1 < ng:
# 答えの候補区間の真ん中について判定問題を解く
k = (ok + ng) // 2
if (R-k)//(x-1) + (B-k)//(y-1) >= k:
ok = k
else:
ng = k
print( ok )こちらから上のコードを試すことが出来ます。
入力に $${{10^{18}}}$$ のような大きい数を入れてもすぐに答えを返すことが確認できると思います。
また、AtCoder で実際にこのコードを提出すれば正解判定ももらえるでしょう。
時間のある方は AtCoder の右上からアカウントを作成すると問題ページの下の方に提出欄が現れると思うので、上のコードを貼り付けて言語の部分を Python(3.8.2) に設定の上提出ボタンを押してみてください。(Python の後の数字は変わっているかもしれません)
結果の欄に正解を表すAC(Accepted の略)の文字が現れると思います。
以上で花束の解説を終わりにします。
ここまで読んで競技プログラミングに興味を持ち始め、既にプログラムもある程度書けるよと言う方がいらっしゃったら、ぜひ以下の類題に挑戦してみてください。
競技プログラミングをやるメリット
最後に手短に競技プログラミングをやるメリットを数点挙げてこの記事を締めようと思います。
本当は競技プログラミングの始め方や勉強の仕方についても書くべきだと思うのですが、それに関してはいろんな方の丁寧な記事や本が既にたくさんあるのでそちらを参考にしてみてください。
分からないことが一切ないのに解けない楽しさ
先ほどの花束と言う問題を知ってみなさんはどう思ったでしょうか。
私はこの問題に挑んだときにはすでにプログラミングについてある程度は理解していましたし、当然競技プログラミングの基本的なルールも把握していました。
競技プログラミングに慣れていた自分にとっては問題内容も非常にシンプルなものであり、読んですぐに理解することが出来ました。
つまり、このとき私はこの問題について何一つ分からないことがない状態でした。
にもかかわらず、私はこの問題を全く解くことが出来ませんでした。
ループも条件分岐も四則演算も全て難なく使いこなせるのですが、それらをどのように組み合わせても、入力される値が大きければ実行に1年以上かかるようなロジックしか思いつかなかったのです。
私たちが普段向き合う問題というのは、経済の動向や他人の意思、複雑な物理法則など、自分には理解できないものや解明されていないものが絡むことがほとんどです。
あるいは目的関数がそもそも定まっていない、いわゆる「正解のない問題」に向き合わないといけないことも多いでしょう。
そういう日々を過ごすうちに「答えのある問題を解くなんて簡単だよ」という思考になってしまう人もいると思います。
しかし先述の通り私は答えのある問題が全く解けませんでした。
私は自分が取れる選択肢を全て把握し、どうなったら正解なのかも完璧に理解しているのですが、どれだけ悩んでも「1秒に10億回の命令をこなせる機械に任せてもどうしても実行に1年以上かかる」方法しか思いつかないのです。
解けないことを自分自身の思考力以外の何にも擦りつけられない中で、せいぜい「絶対に2秒以内に答えを出力する方法が存在する」と言う事実のみを心の支えに考え続けること、そしてそれを世界中の参加者と競い合えることは、この上なく贅沢なことだと思います。
そうして悩んでいた問題が、非常に簡潔でこの上なく鮮やかな方法で、高々60回程度、人間の手作業でも数時間もあれば解けてしまうことを理解した時の感動はすさまじいものでした。
記事を通してこの気持ちを少しでも追体験してもらえていたら幸いです。
このような面白い問題が AtCoder には数千問存在し、現在も毎週増え続けています。
気になった方はぜひ AtCoder を始めてみてくだい。
この調子で全部書いてるとキリがないので残りは箇条書きでサラッと書いてしまいます。
