
多様性はなぜ必要なのか?
以前、ジェームズ・スロウィッキー氏の著書『みんなの意見は案外正しい』を紹介しました。
この本を知ったきっかけは、『「多様な意見」はなぜ正しいのか』で紹介されていたことです。
この本の著者であるスコット・ペイジ氏は、ミシガン大学教授で、複雑系、政治科学、経済学を専門に研究をされています。 前回紹介したコラムニストのジェームズ・スロウィッキー氏の著書よりも専門的な内容になりますが、集団の予測が個人の予測よりも優れていることを簡単な数式を使って「多様性予測定理」として証明されているところが興味深いです。
一部を紹介しますと、下記の表は予測者2名(aさんとbさん)が、学校のテストで対象A,B,Cさんの順位を予測したものです。例えば、対象Aさんについて、予測者aさんは6位と予測、予測者bさんは8位と予測、平均(予測者aさんと予測者bさんの平均)で8位、結果は6位でした。それを基に以下の計算をします。
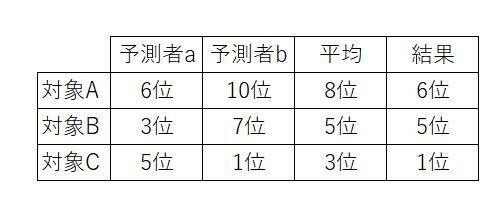
予測者aの平均誤差:(6-6)^2+(3-5)^2+(5-1)^2=0+4+16=20
予測者bの平均誤差:(10-6)^2+(7-5)^2+(1-1)^2=16+4+0=20
平均個人誤差:(20+20)/2=20
集団的誤差:(8-6)^2+(5-5)^2+(3-1)^2=8
上記の結果より
「集団的誤差<平均個人誤差」が導かれます
これは、今回の例だけではなく常に成立すると説明されています。
ここでの説明はこれまでにしますが、ご興味ある方は本で読んでみてください。
またペイジ氏は、「個人の平均的能力と高める」ことと「多様性を高める」ことは、等しく集団の予測を高めることに寄与すると導いています。
本文では、「“違う”ことは、“良い”ことと同じくらい大切」という表現をされています。
今日のお話は、あくまでも計算上の話です。
現実は、計算通りには上手くいきません。
「1+1=2」になることもあれば、「1+1<2」や「1+1>2」にもなります。計算通りに進まないことが、“人”の面白さだと思います。
アカデミーヒルズ 熊田ふみ子
※タイトルの画像は、アカデミーヒルズ内にある「ラウンジ49」で販売されているパンです。1種類のパンよりも、色々な種類のパンが並んでいる方が魅力的ですよね。パンも多様な方がいいなと思い、この写真を撮りました。
