統計学的アプローチによる競馬予想（線形モデル編）

2024年7月14日 20:04

過去10年間のレース情報を分析して定量的に競馬予想する方法を考えたので、過程と結果を共有します。
ここでは、シンプルな統計モデル（線形回帰モデル）を考えます。
※予測精度を重視した複雑なモデルは別記事参照。

今回は「業務効率化」テーマから外れて競馬ネタの投稿です。

概要

基本方針

はじめに、軸がブレないように基本方針を定めておきます。
・ランニングコスト無料でレース予想する
・中央競馬に絞ってレース予想する
・使い勝手を考慮し、シンプルな統計モデルを考える

分析する上で大量のデータを扱うので、効率を考えて統計ソフト「R」を使います。検証では「R」を使いますが、最終的には四則演算で計算可能な回帰式にまとめるので、結論さえ分かれば、VBAなどの他言語に移植して活用できる（恩恵は受けられる）と思います。

データの整理

まず、どんなデータが手に入るのか整理します。
大きく分けて２つ。

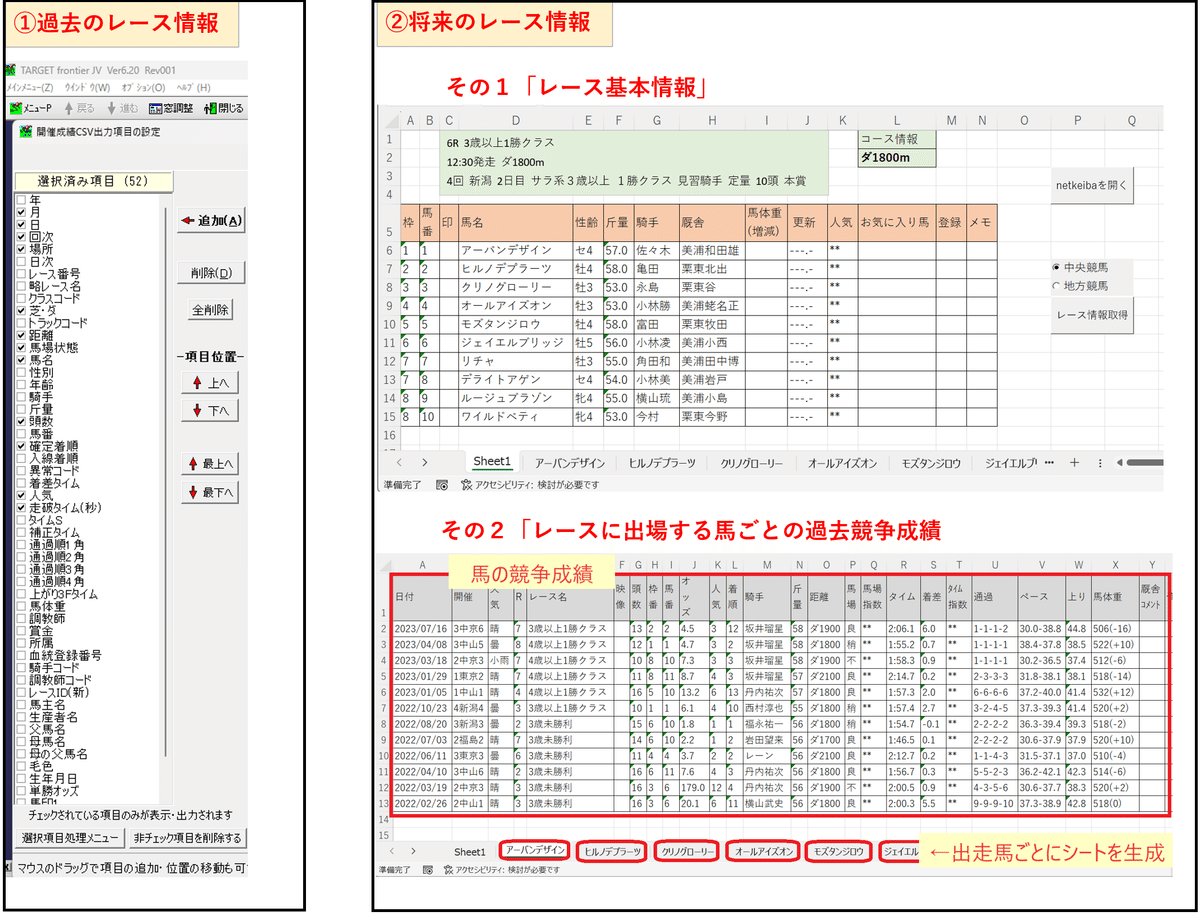
①過去のレース情報
JRA-VANを使えば過去30年間のJRA全レース情報が手に入ります。
※JRA-VANは有料サービスですが、初回のみ無料体験期間あり。
　必要な情報をCSV形式でダウンロードしたら、料金発生する前に解約。
直近10年間のデータに絞ってみると約54万件見つかりました。
これをモデル構築用の学習データとします。

②将来のレース情報
実際に予想したいレースの情報（コース情報や出走馬情報）です。
無料で閲覧できるnetkeibaの掲載情報を情報源とします。
これを予測用のテストデータとします。
　→具体的には…
　その１「コース基本情報」
　　・開催場所
　　・コース（芝orダート）
　　・距離（m）
　　・馬名
　　・騎手名
　その２「出走馬の過去競争成績」
　　・開催場所
　　・コース（芝orダート）
　　・距離（m）
　　・条件（良/稍重など）
　　・天気
　　・斤量
　　・馬体重などなど…。
といった情報がテストデータとして活用できそうです。
折角なのでnetkeibaから情報取得するExcelツールをそのまま使って、テストデータを用意します。

作戦

以上を踏まえて、作戦を考えます。
１．学習データから、統計モデル※を作成。
　　目的変数Y：タイム（秒）
　　説明変数X：開催場所・コース・距離・条件など…
２．テストデータ（説明変数Xの項目）を統計モデルへ代入。
　　結果として、目的変数Yである期待値（つまり予測タイム）を得る。
３．期待値（予測タイム）と、実際の走破タイムの残差を計算。
　　残差を馬ごとに集計することで、各馬のポテンシャル（優劣）を判断。

つまり、54万件の学習データから当てはまりの良い一般的な統計モデル※を作成し、テストデータ内に存在する出走馬（の過去競争成績）が一般的に見てどの程度良い（あるいは悪い）タイムを出していたのかを数値化し、その数値を馬ごとに集計・比較することでレース順位を予想しよう、という発想です。
※1つのYと複数のXを用いた重回帰分析とします。
　予測精度を求めすぎて複雑なモデルを作っても使い勝手が悪い（かつ運用面を考慮するとXは「無料取得できる情報」に限定する必要あり）ので、解釈を優先してここではXに対する一次式（線形回帰モデル）を考えます。

統計モデル構築

統計モデルとは、現象を簡略化して数式的に表現するための枠組みです。
統計モデルをどう考えるか…。

線形回帰モデルの考え方

タイム（Y）とそれに影響を与える各要素（X）に分けて考えます。
まず、Yに対する影響度合いから判断してXを4要因に絞りました。
目的変数 (Y): タイム（秒）
　　→量的変数
説明変数 (X1): 距離（m）　
　　→量的変数
説明変数 (X2): 条件
　　→｛良、稍重、重、不良｝の4個のカテゴリカル変数
説明変数 (X3): 開催場所
　　→｛東京、中山、京都、阪神、中京、新潟、札幌、函館、福島、小倉｝
　　の10個のカテゴリカル変数
説明変数 (X4): コース
　　→｛芝、ダート｝の2個のカテゴリカル変数

y=a+bX1+cX2+dX3+eX4+ε
※aは切片、b,c,d,eはそれぞれの回帰係数、εは確率誤差。

ただし、まだちょっと次元数が多いですね。
X4について、それぞれ「コース＝芝」のとき、「コース=ダート」のときの２つに切り分けて運用することで次元削除します。
y=a+bX1+cX2+dX3+ε

更に、レース距離によって、馬が全力で走れるペースは変わってくると考えられるので、短・中・長距離の３つに条件分けしてモデル運用するのが合理的です。
距離に応じて、
　・短距離：1400m以下
　・中距離：1500m ～ 2000m
　・長距離：2100m 以上
という３つのレンジへデータ分割して考える運用とします。
→なので、コース2通り×距離3通り＝計6通りの統計モデルを使い分ける運用とします。

なお、説明変数X2「条件」と、説明変数X3「開催場所」は互いに相乗効果があるものとして（＝交互作用有りとして）考えます。
※例えば、新潟競馬場は水はけが良くタイムが出やすい、中京競馬場は粘土質で泥濘がちでタイムに傾斜が掛かりやすい等の特性の掛け算を考慮。
交互作用項を加えて、y=a+bX1+cX2+dX3+eX2X3+ε。

この線形回帰モデル（y=a+bX1+cX2+dX3+eX2X3+ε）について、計6通りの回帰式を求めていきます。

過去10年間のレース情報（学習データの準備）

回帰モデルを求めるために、まずは過去レース結果を入手します。
JRA-VANのTARGET frontier JVをインストールして、直近10年間のレース情報（約54万件）をCSV形式でダウンロードしましょう。

CSV形式でダウンロードしたら、こんな感じで1行目に列名を振っておきます。使う列名は「場所」「コース」「距離」「条件」「タイム」の５つ。

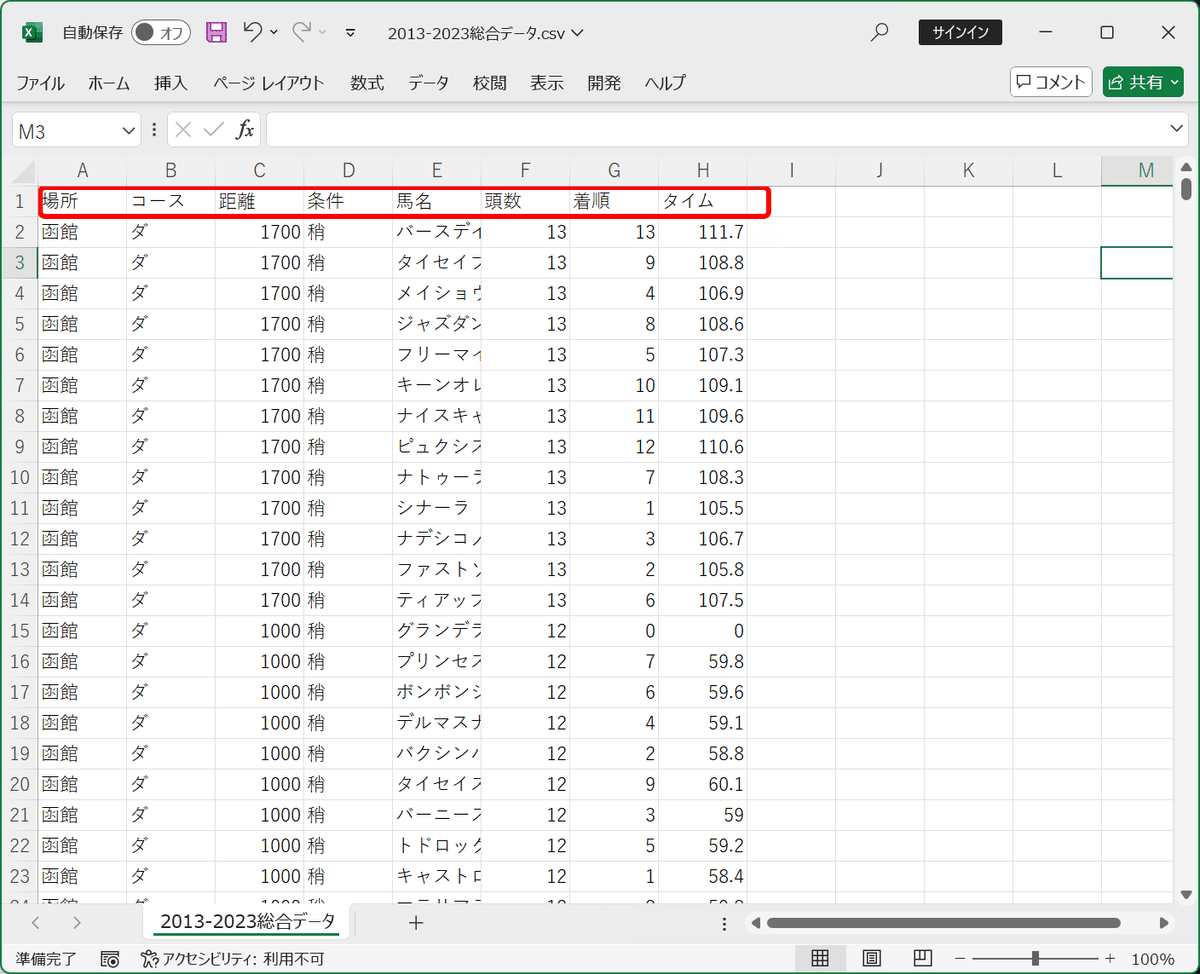
分析に使う学習データは、こんな感じのCSVデータです。
※Excelで開いた場合は、CSV UTF-8（コンマ区切り）（*.csv）形式で保存。

最小二乗法で線形回帰モデルを推定

続いて、このCSVファイルを統計ソフトRで分析します。
Rの導入方法は割愛。
Rのディレクトリ設定と、CSVファイル名の設定を忘れずに。
【ここでの処理内容】
１．CSVファイルを読込み
２．「条件＝芝」「条件＝ダート」の2種類にデータ分割
３．さらに「距離」で3種類にデータ分割し、計６つのモデル作成

data.tableパッケージのfread関数を使ってCSVファイルを読込み、約54万件のデータをdata.tableオブジェクトで扱います。「条件」や「距離」のソートには[演算子を使用。なおカテゴリカル変数内の各文字列にはダミー変数を振って数値化しておき、その際「場所＝東京」「条件＝良」を基準（値＝０）としました。
線形回帰モデルの作成は、通常のlm関数だとメモリ不足になるためbiglm関数を使って分割しながら回帰式を計算します。lm関数もbiglm関数も最小二乗法（データとの残差平方和を最小化するように切片と傾きを決定する）による回帰式の推定です。

# パッケージ読込み（未インストールならばインストール処理）
packages <- c("data.table", "biglm")
for (pkg in packages) {
  if (!require(pkg, character.only = TRUE)) {
    install.packages(pkg)
    library(pkg, character.only = TRUE)
  }
}

# 5万件づつデータを読込んで、直線回帰モデルを構築する関数
New_Model <- function(Data, formula, Chunk = 50000) {
  if (nrow(Data) <= Chunk) {
    biglm(formula, data = Data)
  } else {
    FirstChunk <- Data[1:Chunk, ]
    Model <- biglm(formula, data = FirstChunk)
    for (i in seq(Chunk + 1, nrow(Data), by = Chunk)) {
      end <- min(i + Chunk - 1, nrow(Data))
      Model <- update(Model, Data[i:end, ])
    }
    Model
  }
}

# 過去10年間のCSVデータ読込み＆整形する関数
# 場所＝東京、条件＝良を基準(0)とする。
Cleaning_Data <- function(Cource) {
  AllData <- fread("2013-2023総合データ.csv")
  AllData <- AllData[!is.na(タイム) & タイム != 0 & !is.na(距離) & !is.na(条件) & !is.na(場所) & !is.na(コース) & 着順 != 0 & コース == Cource,]
  AllData[, 場所 := factor(場所, levels = c("東京", unique(場所[場所 != "東京"])))]
  AllData[, 条件 := factor(条件, levels = c("良", unique(条件[条件 != "良"])))]
  return(AllData)
}

# 過去10年間のCSVデータを、芝とダートの2種類に大別
AllData芝 <- Cleaning_Data("芝")
AllDataダ <- Cleaning_Data("ダ")

# 線形回帰モデルの式定義（目的変数=タイム、説明変数＝距離、条件、場所）
# 条件と場所の交互作用あり
formula <- as.formula("タイム ~ 距離 + 条件 * 場所")

# 距離（Short, Medium, Long）とコース(芝, ダート)、計６パターンのモデルを構築
芝Short_Model <- New_Model(AllData芝[距離 <= 1400], formula)
芝Medium_Model <- New_Model(AllData芝[距離 > 1400 & 距離 < 2100], formula)
芝long_Model <- New_Model(AllData芝[距離 >= 2100], formula)
ダShort_Model <- New_Model(AllDataダ[距離 <= 1400], formula)
ダMedium_Model <- New_Model(AllDataダ[距離 > 1400 & 距離 < 2100], formula)
ダlong_Model <- New_Model(AllDataダ[距離 >= 2100], formula)

# 構築したモデルを表示
summary(芝Short_Model)
summary(芝Medium_Model)
summary(芝long_Model)
summary(ダShort_Model)
summary(ダMedium_Model)
summary(ダlong_Model)

目的変数：Y=タイム
説明変数：X1=距離、X2=条件、X3=場所。
なお、X2は「良」のときを、X3は「東京」のときをそれぞれ基準（値＝０）として回帰係数を導出します。
これを実行すると、モデル名「芝Short_Model」「芝Medium_Model」「芝Long_Model」「ダShort_Model」「ダMedium_Model」「ダLong_Model」という６つの線形回帰モデルが作られます。

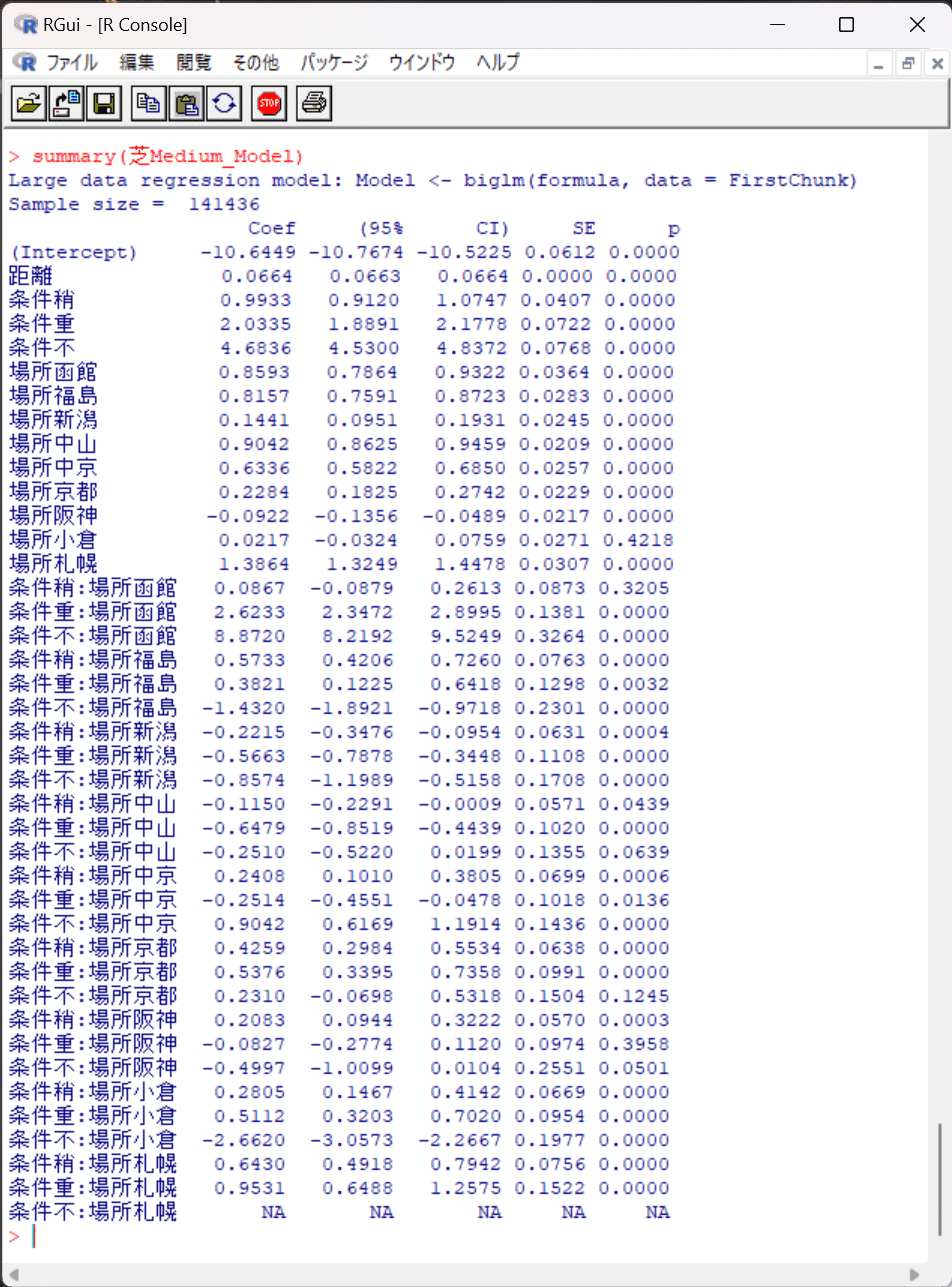
例えばモデル名「芝Short_Model」の中身を覗いてみると…

このサマリーから、モデル名「芝Short_Model」の回帰式は次のように書けます。
タイム=−9.3242+0.0658×距離+1.7795×D条件重+4.2525×D条件不+0.6143×D条件稍-0.2282×D京都-0.0685×D阪神+0.6606
×D札幌+ …（中略）… + ε
※なおDはダミー変数を表す。当該条件のときは1、そうでないときは0。
→これら切片と回帰係数さえ分かってしまえば、あとは四則演算だけで目的変数Yであるタイムが導出可能。

補足：モデルの妥当性検証

ところで、次のステップへ進む前にモデルの妥当性を確認しておきます。
どう検証するかというと…
・全データの８割をモデル構築用に、残り２割をモデル検証用に分ける。
・モデル構築用データを使って、先ほど同様にモデル構築。
・モデル検証用データを使って、構築したモデルとの適合度合いを判別。

ということで、適合度合いに関する統計量を計算します。
【ここでの処理内容】
１．CSVファイルを読込み
２．「条件＝芝」「条件＝ダート」の2種類にデータ分割
３．それぞれのデータに対し、8割を構築用、2割を検証用にデータ分割
４．構築用データをさらに「距離」で3種類に分割し、計６つのモデル作成
５．検証用データをモデルへ代入し、期待値（目的変数Yの期待値）を計算
６．期待値（目的変数Yの期待値）と実際のデータ（検証用データ）の残差を計算し、モデル毎に残差の統計量を作成

# パッケージ読込み（未インストールならばインストール処理）
packages <- c("data.table", "biglm")
for (pkg in packages) {
  if (!require(pkg, character.only = TRUE)) {
    install.packages(pkg)
    library(pkg, character.only = TRUE)
  }
}

# 5万件づつデータを読込んで、直線回帰モデルを構築する関数
New_Model <- function(Data, formula, Chunk = 50000) {
  if (nrow(Data) <= Chunk) {
    biglm(formula, data = Data)
  } else {
    FirstChunk <- Data[1:Chunk, ]
    Model <- biglm(formula, data = FirstChunk)
    for (i in seq(Chunk + 1, nrow(Data), by = Chunk)) {
      end <- min(i + Chunk - 1, nrow(Data))
      Model <- update(Model, Data[i:end, ])
    }
    Model
  }
}

# 過去10年間のCSVデータ読込み＆整形する関数
# 場所＝東京、条件＝良を基準(0)とする。
Cleaning_Data <- function(Cource) {
  AllData <- fread("2013-2023総合データ.csv")
  AllData <- AllData[!is.na(タイム) & タイム != 0 & !is.na(距離) & !is.na(条件) & !is.na(場所) & !is.na(コース) & 着順 != 0 & コース == Cource,]
  AllData[, 場所 := factor(場所, levels = c("東京", unique(場所[場所 != "東京"])))]
  AllData[, 条件 := factor(条件, levels = c("良", unique(条件[条件 != "良"])))]
  return(AllData)
}

# データをTrainとTestに分割する関数
Split_Data <- function(Data, split_ratio = 0.8) {
  set.seed(123)  # 再現性のためのシード設定
  trainIndex <- sample(seq_len(nrow(Data)), size = floor(split_ratio * nrow(Data)))
  TrainData <- Data[trainIndex, ]
  TestData <- Data[-trainIndex, ]
  list(TrainData = TrainData, TestData = TestData)
}

# 過去10年間のCSVデータを、芝とダートの2種類に大別
AllData芝 <- Cleaning_Data("芝")
AllDataダ <- Cleaning_Data("ダ")

# データ分割
芝Split <- Split_Data(AllData芝)
ダSplit <- Split_Data(AllDataダ)
TrainData芝 <- 芝Split$TrainData
TestData芝 <- 芝Split$TestData
TrainDataダ <- ダSplit$TrainData
TestDataダ <- ダSplit$TestData

# 線形回帰モデルの式定義（目的変数=タイム、説明変数＝距離、条件、場所）
# 条件と場所の交互作用あり
formula <- as.formula("タイム ~ 距離 + 条件 * 場所")

# 距離（Short, Medium, Long）とコース(芝, ダート)、計６パターンのモデルを構築
芝Short_Model <- New_Model(芝Split$TrainData[距離 <= 1400], formula)
芝Medium_Model <- New_Model(芝Split$TrainData[距離 > 1400 & 距離 < 2100], formula)
芝long_Model <- New_Model(芝Split$TrainData[距離 >= 2100], formula)
ダShort_Model <- New_Model(ダSplit$TrainData[距離 <= 1400], formula)
ダMedium_Model <- New_Model(ダSplit$TrainData[距離 > 1400 & 距離 < 2100], formula)
ダlong_Model <- New_Model(ダSplit$TrainData[距離 >= 2100], formula)

# 構築したモデルを表示
summary(芝Short_Model)
summary(芝Medium_Model)
summary(芝long_Model)
summary(ダShort_Model)
summary(ダMedium_Model)
summary(ダlong_Model)
# ---------------（ここまでがTrainDataを使ったモデル構築）
# ---------------（ここからがTestDataを使ったモデル検証）

# 第一引数Dataを第二引数Modelに代入することで予測タイムを計算し、Dataの「予測タイム」列に追加する関数
Calc_ExpectedValue <- function(Data, Model) {
  if (nrow(Data) > 0) {
    coefficients <- coef(Model)
    切片 <- coefficients[1]
    距離指数 <- coefficients["距離"] * Data$距離
    条件指数 <- sapply(Data$条件, function(strCond) {
      if (strCond == "良") return(0) else return(coefficients[paste0("条件", strCond)])
    })
    場所指数 <- sapply(Data$場所, function(place) {
      if (place == "東京") return(0) else return(coefficients[paste0("場所", place)])
    })
    場所と条件の交互作用指数 <- mapply(function(strCond, place) {
      if (strCond == "良" || place == "東京") {
        return(0)
      } else {
        coeff_name <- paste0("条件", strCond, ":場所", place)
        if (coeff_name %in% names(coefficients)) {
          return(coefficients[coeff_name])
        } else {
          return(0)
        }
      }
    }, Data$条件, Data$場所)
    期待値 <- 切片 + 距離指数 + 条件指数 + 場所指数 + 場所と条件の交互作用指数
    Data$予測タイム <- 期待値
  } else {
    Data$予測タイム <- NA
  }
  return(Data)
}

# F分布を用いてp値を求める関数（F値, 自由度, サンプル数）
Calc_p_value <- function(f_value, p, n) {
  p_value <- pf(f_value, df1 = p, df2 = n - p - 1, lower.tail = FALSE)
  return(p_value)
}

# 統計値を計算する関数
Calc_Statistics <- function(Data, Model) {
  Data <- Calc_ExpectedValue(Data, Model)  # 予測タイムを計算
  SS_res <- sum((Data$タイム - Data$予測タイム)^2)  #残差平方和
  SS_tot <- sum((Data$タイム - mean(Data$タイム))^2)  #全変動
  p <- sum(!is.na(coef(Model)))  #モデルの有効な係数の数=自由度
  n <- nrow(Data) #サンプルサイズ
  SS_reg <- SS_tot - SS_res  #回帰平方和（モデルによる変動）
  F_value <- (SS_reg / p) / (SS_res / (n - p - 1))  #F値
  R_squared <- SS_reg / SS_tot  #決定係数 R^2
  Adjusted_R_squared <- 1 - ((1 - R_squared) * (n - 1) / (n - p - 1))  #調整済み決定係数
  # p値を計算
  p_Value <- Calc_p_value(F_value, p, n)
  # 結果をリストで返す
  return(list(F_value = F_value, R_squared = R_squared, Adjusted_R_squared = Adjusted_R_squared, p_Value = p_Value))
}

# 各モデルに対して統計値を計算
Stats_ダShort <- Calc_Statistics(TestDataダ[距離 <= 1400], ダShort_Model)
Stats_芝Short <- Calc_Statistics(TestData芝[距離 <= 1400], 芝Short_Model)
Stats_ダMedium <- Calc_Statistics(TestDataダ[距離 > 1400 & 距離 < 2100], ダMedium_Model)
Stats_芝Medium <- Calc_Statistics(TestData芝[距離 > 1400 & 距離 < 2100], 芝Medium_Model)
Stats_ダLong <- Calc_Statistics(TestDataダ[距離 >= 2100], ダlong_Model)
Stats_芝Long <- Calc_Statistics(TestData芝[距離 >= 2100], 芝long_Model)

# 結果の表示
print(Stats_ダShort)
print(Stats_芝Short)
print(Stats_ダMedium)
print(Stats_芝Medium)
print(Stats_ダLong)
print(Stats_芝Long)

実行結果を纏めると、こうなりました。

F値：モデルが統計的に有意かどうかを判断。値が高ければ高いほど、モデルの説明変数が目的変数の変動を有意に説明していると解釈。
決定係数 (R²)：モデルがデータの分散の〇％を説明できていることを示す。
例えば「ダShort_Model」ならデータの95.6％を説明していることを示し、モデルの説明力（つまり当てはまりの良さ）を表す。
調整済み決定係数 (R'²)：説明変数の数に応じて、決定係数を修正したもの。
p値：統計的にどの程度有意かを判断する目安。
→F値が高く、R'²も1に近いため説明力は高いと言える。（厳しく見るなら「ダMedium_Model」だけは若干劣るが…）

予測タイムの算出

さて、学習データから統計モデルを構築できたので、ここからは実際にレースで走る馬のデータ（テストデータ）を使用して分析していきます。

出走馬の過去競争成績（テストデータの準備）

冒頭でも書きましたが、「ランニングコスト無料で予測すること」を前提とするので、netkeibaから情報取得するExcelツールをそのまま活用します。
このツールの機能①を使って、各馬の過去競争成績をWebから入手します。さらに続けて、以下の「CreateCSV」プロシージャ（VBAコード）を実行すると、各馬の競争成績をCSVファイルに保存できます。

'各馬の競争成績をCSVファイルに書き出すVBAコード

Private Sub CreateCSV()
  Application.ScreenUpdating = False
  Application.DisplayAlerts = False
  Dim FolderPath As String
  Dim fso As Object
  Dim Folder As Object
  Dim File As Object
  Dim sh As Worksheet
  Dim FilePath As String
  FolderPath = "C:\Users\******\各馬のデータ"  '任意のフォルダパスを設定
  
  'フォルダ内のリセット
  Set fso = CreateObject("Scripting.FileSystemObject")
  Set folder = fso.GetFolder(FolderPath)
  For Each file In folder.Files
    file.Delete
  Next
  
  '各シート情報をCSVへ書き出す
  For Each sh In Worksheets
    If sh.Name = "Sheet1" Or sh.Name = "Sheet2" Then
      sh.Delete
    Else
      If sh.Range("A2").Value <> "" Then
        Call CreateCSVdata(sh)
        FilePath = FolderPath & "\" & sh.Name & ".csv"
        ' 一時的に新しいワークブックを作成して、アクティブシートをコピー
        sh.Copy
        With ActiveWorkbook
          .SaveAs Filename:=FilePath, FileFormat:=xlCSVUTF8  'CSV UTF-8 形式で保存
          .Close SaveChanges:=False
        End With
      End If
    End If
  Next
  Application.ScreenUpdating = True
  Application.DisplayAlerts = True
End Sub


Private Sub CreateCSVdata(ByVal sh As Worksheet)
  'シート情報を取得
  Dim Base As Range
  Dim MaxRow As Long
  Dim Target() As Variant
  Set Base = sh.Range("A1")
  MaxRow = Base.CurrentRegion.Rows.Count
  Target() = Base.Offset(1).Resize(MaxRow - 1, 28).Value
  If MaxRow <= 1 Then Exit Sub

  '欲しい情報（場所・コース・距離・条件・頭数・着順）のみを抽出して、配列RaceData()へ格納
  Dim RaceData() As Variant
  Dim i As Integer
  ReDim RaceData(MaxRow - 1, 7)
  For i = 0 To MaxRow - 2
    '場所の代入
    Dim isValid As Boolean
    Dim validVenues As Variant
    Dim venue As Variant
    isValid = False
    validVenues = Array("東京", "中山", "京都", "阪神", "中京", "新潟", "札幌", "函館", "福島", "小倉")
    For Each venue In validVenues
      If Mid(Target(i + 1, 2), 2, 2) = venue Then
        isValid = True
        Exit For
      End If
    Next
    If isValid = True Then
      RaceData(i, 0) = Mid(Target(i + 1, 2), 2, 2) '場所
    Else
      RaceData(i, 0) = ""
    End If
    
    'コースの代入
    isValid = False
    validVenues = Array("ダ", "芝")
    For Each venue In validVenues
      If Left(Target(i + 1, 15), 1) = venue Then
        isValid = True
        Exit For
      End If
    Next
    If isValid = True Then
      RaceData(i, 1) = Left(Target(i + 1, 15), 1) 'コース
    Else
      RaceData(i, 1) = ""
    End If
    
    RaceData(i, 2) = Mid(Target(i + 1, 15), 2) '距離
    
    '条件の代入
    isValid = False
    validVenues = Array("良", "稍", "重", "不")
    For Each venue In validVenues
      If Target(i + 1, 16) = venue Then
        isValid = True
        Exit For
      End If
    Next
    If isValid = True Then
      RaceData(i, 3) = Target(i + 1, 16) '条件
    Else
      RaceData(i, 3) = ""
    End If
    
    '頭数、着順の代入
    RaceData(i, 4) = Left(Target(i + 1, 7), 1) '頭数
    RaceData(i, 5) = Target(i + 1, 12) '着順
    
    'タイムの代入
    Dim parts() As String
    If InStr(Target(i + 1, 18), ":") > 0 Then
      parts = Split(Target(i + 1, 18), ":") ':で文字列を分割
      RaceData(i, 6) = Replace(CDbl(parts(0)) * 60 + CDbl(parts(1)), " ", "") 'タイム
    End If
  Next
  
  '貼付け用配列を作成
  Dim PasteData As Variant
  ReDim PasteData(7, 1)
  PasteData(0, 0) = "場所"
  PasteData(1, 0) = "コース"
  PasteData(2, 0) = "距離"
  PasteData(3, 0) = "条件"
  PasteData(4, 0) = "頭数"
  PasteData(5, 0) = "着順"
  PasteData(6, 0) = "タイム"
  
  ' 有効な行をコピー
  Dim j As Integer
  Dim k As Integer
  k = 1
  For i = 0 To UBound(RaceData) - 1
    If RaceData(i, 0) <> "" And RaceData(i, 1) <> "" And RaceData(i, 2) <> "" And RaceData(i, 3) <> "" And RaceData(i, 4) <> "" And RaceData(i, 5) <> "" And RaceData(i, 6) <> "" Then
      ReDim Preserve PasteData(7, k + 1)
      For j = 0 To 6
        PasteData(j, k) = RaceData(i, j)
      Next
      k = k + 1
    End If
  Next
  
  'シートに貼付け
  sh.Cells.Clear
  With Base.Resize(UBound(PasteData, 2), UBound(PasteData) + 1)
    .Value = WorksheetFunction.Transpose(PasteData)
    .EntireColumn.AutoFit
  End With
End Sub

※ただし、変数FolderPathは任意のフォルダパスへ書き換えてください。
これを実行すると、下図のようなCSVファイルが全馬分生成されます。

これをテストデータとします。
テストデータを、先ほど構築した線形回帰式へ代入していきます。

テストデータを統計モデルへ代入して期待値を計算

各馬のCSVデータが準備できたら、これをRで読込んで、条件（芝orダート）と距離（短距離・中距離・長距離）にソートしてから、6つのうち適切なモデルへ代入することで、目的変数Yであるタイム（つまり予測タイム）を得ます。
ここでの予測タイムとは、各説明変数から導かれる期待値です。この条件だったら走破タイムの平均は〇〇秒だろう、という意味合いです。

【ここでの処理内容】
１．CSVファイルを読込み
２．条件と距離に応じて６つのデータサブセットへ分割
３．それぞれのデータに応じたモデルを選択し、値をモデルへ代入
　　（計算結果は、「予測タイム」列へ書き込む）
４．各馬の実績（「タイム」列）と、期待値（「予測タイム」列）の残差を計算。
５．馬ごとに残差の平均値を取得し、並び替えて表示。


# ---------------（ここからが実際のレース出走馬の成績を使った期待値算出）

# CSV ファイルを読み込む関数
Sorting_CSV <- function(FileName) {
  InputData <- fread(FileName)
  list(
    Soted_ダShort = InputData[コース == "ダ" & 距離 <= 1400][, `:=`(
      場所 = factor(場所, levels = levels(AllDataダ$場所)),
      条件 = factor(条件, levels = levels(AllDataダ$条件))
    )],
    Soted_芝Short = InputData[コース == "芝" & 距離 <= 1400][, `:=`(
      場所 = factor(場所, levels = levels(AllData芝$場所)),
      条件 = factor(条件, levels = levels(AllData芝$条件))
    )],
    Soted_ダMedium = InputData[コース == "ダ" & 距離 > 1400 & 距離 < 2100][, `:=`(
      場所 = factor(場所, levels = levels(AllDataダ$場所)),
      条件 = factor(条件, levels = levels(AllDataダ$条件))
    )],
    Soted_芝Medium = InputData[コース == "芝" & 距離 > 1400 & 距離 < 2100][, `:=`(
      場所 = factor(場所, levels = levels(AllData芝$場所)),
      条件 = factor(条件, levels = levels(AllData芝$条件))
    )],
    Soted_ダLong = InputData[コース == "ダ" & 距離 >= 2100][, `:=`(
      場所 = factor(場所, levels = levels(AllDataダ$場所)),
      条件 = factor(条件, levels = levels(AllDataダ$条件))
    )],
    Soted_芝Long = InputData[コース == "芝" & 距離 >= 2100][, `:=`(
      場所 = factor(場所, levels = levels(AllData芝$場所)),
      条件 = factor(条件, levels = levels(AllData芝$条件))
    )]
  )
}

# 第一引数Dataを第二引数Modelに代入することで予測タイムを計算し、Dataの「予測タイム」列に追加する関数
Calc_ExpectedValue <- function(Data, Model) {
  if (nrow(Data) > 0) {
    coefficients <- coef(Model)
    切片 <- coefficients[1]
    距離指数 <- coefficients["距離"] * Data$距離
    条件指数 <- sapply(Data$条件, function(strCond) {
      if (strCond == "良") return(0) else return(coefficients[paste0("条件", strCond)])
    })
    場所指数 <- sapply(Data$場所, function(place) {
      if (place == "東京") return(0) else return(coefficients[paste0("場所", place)])
    })
    場所と条件の交互作用指数 <- mapply(function(strCond, place) {
      if (strCond == "良" || place == "東京") {
        return(0)
      } else {
        coeff_name <- paste0("条件", strCond, ":場所", place)
        if (coeff_name %in% names(coefficients)) {
          return(coefficients[coeff_name])
        } else {
          return(0)
        }
      }
    }, Data$条件, Data$場所)
    期待値 <- 切片 + 距離指数 + 条件指数 + 場所指数 + 場所と条件の交互作用指数
    Data$予測タイム <- 期待値
  } else {
    Data$予測タイム <- NA
  }
  return(Data)
}

# フォルダ内の全てのCSVファイルを取得
setwd("C:/Users/******/各馬のデータ")  #任意のフォルダパスを設定
CSVs <- list.files(pattern = "*.csv")

# 空のリストを作成
ExpectedValue_All_list <- list()

# CSVファイル毎に予測タイム(期待値)列を加えたデータを作成し、リストExpectedValue_All_listへ格納する
for (FileName in CSVs) {
  DataSet <- Sorting_CSV(FileName)
  ExpectedValue_ダShort <- Calc_ExpectedValue(DataSet$Soted_ダShort, ダShort_Model)
  ExpectedValue_芝Short <- Calc_ExpectedValue(DataSet$Soted_芝Short, 芝Short_Model)
  ExpectedValue_ダMedium <- Calc_ExpectedValue(DataSet$Soted_ダMedium, ダMedium_Model)
  ExpectedValue_芝Medium <- Calc_ExpectedValue(DataSet$Soted_芝Medium, 芝Medium_Model)
  ExpectedValue_ダLong <- Calc_ExpectedValue(DataSet$Soted_ダLong, ダlong_Model)
  ExpectedValue_芝Long <- Calc_ExpectedValue(DataSet$Soted_芝Long, 芝long_Model)

  ExpectedValue_All <- rbind(
  ExpectedValue_ダShort,
  ExpectedValue_芝Short,
  ExpectedValue_ダMedium,
  ExpectedValue_芝Medium,
  ExpectedValue_ダLong,
  ExpectedValue_芝Long
  )
  ExpectedValue_All_list[[FileName]] <- ExpectedValue_All
}

# リストExpectedValue_All_listの中身を表示
for (FileName in CSVs) {
  cat("\nResults for", FileName, ":\n")
  print(ExpectedValue_All_list[[FileName]])
}

# ディレクトリを設定（もとに戻す）
setwd("C:/Users/******")

# ---------------（ここからが各馬の成績と期待値の乖離具合を分析する処理）

# 各レース毎の残差（タイム－予測タイム）、各馬毎の統計量（平均残差・標準偏差）を計算する関数
# NAがない行で残差を計算
Calc_Residuals <- function(Predictions, HorseName) {
  Predictions <- Predictions[!is.na(タイム) & !is.na(予測タイム), 残差 := タイム - 予測タイム]
  # 馬名と統計量を含むデータフレームを作成
  data.table(
    馬名 = HorseName,
    平均残差 = mean(Predictions$残差, na.rm = TRUE),
    標準偏差 = sd(Predictions$残差, na.rm = TRUE)
  )
}

# リストの各要素（各馬のデータ）に対してCalc_Residualsを呼び出して、残差の統計量を取得する関数
AllHorsePerformance <- lapply(names(ExpectedValue_All_list), function(name) {
  HorseName <- gsub(".csv", "", name)
  Calc_Residuals(ExpectedValue_All_list[[name]], HorseName)
})

# 各馬のデータを縦に連結（行を追加する形で結合）し、平均残差で降順に並び替え
FinalPerformance <- rbindlist(AllHorsePerformance)
setorder(FinalPerformance, -平均残差)
print(FinalPerformance)

これを実行すると、下図のような結果が表示されます。
平均残差は、正の場合は予測タイム（＝期待値）からどれだけ遅いか、負の場合はどれだけ早いかを秒単位で表示しています。数字が小さいほど良いタイムを過去レースで残していたことになります。
この例だと、馬ごとの過去競争成績から判断して「パウオレ」が最も早い実績を残していた（ポテンシャルが高い馬）と見る事が出来ます。

更にこの結果を視覚化したい場合は…

# 必要なライブラリをロード
packages <- c("ggplot2")
for (pkg in packages) {
  if (!require(pkg, character.only = TRUE)) {
    install.packages(pkg)
    library(pkg, character.only = TRUE)
  }
}

# ggplotを使用してデータを視覚化
ggplot(FinalPerformance, aes(x = reorder(馬名, 平均残差), y = 平均残差, fill = 馬名)) +
  geom_col(show.legend = FALSE) +  # 棒グラフ、凡例非表示
  geom_errorbar(aes(ymin = 平均残差 - 標準偏差, ymax = 平均残差 + 標準偏差), width = .2, color = "black") +  # エラーバー
  geom_text(aes(label = sprintf("%.2f", 平均残差)), position = position_dodge(width = 0.9), vjust = -0.5, size = 3, color = "black") +  # ラベルの追加
  labs(title = "馬別の平均残差と標準偏差", x = "馬名", y = "平均残差") +
  theme_minimal() +
  theme(axis_text_x = element_text(angle = 90, hjust = 1),  # X軸のラベルを縦に表示
        axis_title = element_text(size = 12),  # 軸ラベルのフォントサイズ
        plot_title = element_text(size = 14, face = "bold"))  # タイトルのフォント設定

実行結果はこんな感じ。

「パウオレ」の平均残差が一番小さくて速いですが、同時に標準誤差であるエラーバーの範囲も広いです…。標準誤差が大きいということは、予測タイムと実際のタイムの差異（残差）のばらつきが大きい（＝不確実性が高い）という事です。
こんな感じで、出走馬を比較することが出来ました。

個人的には、今回の方法でぴったりと順位を予想するような運用ではなく、最後の棒グラフのように馬ごとのポテンシャルを視覚化することで、明らかに期待値が低い馬を候補から除外するために使う運用がよいかなーと思っています。

最後に、モデル構築から馬ごとの期待値を算出するまでの処理を全部繋げたRコードを載せておきます。（内容は前述と同じ）
※CSVファイルのフォルダパスと作業ディレクトリは適宜書き換えてください。

# パッケージ読込み（未インストールならばインストール処理）
packages <- c("data.table", "biglm")
for (pkg in packages) {
  if (!require(pkg, character.only = TRUE)) {
    install.packages(pkg)
    library(pkg, character.only = TRUE)
  }
}

# 5万件づつデータを読込んで、直線回帰モデルを構築する関数
New_Model <- function(Data, formula, Chunk = 50000) {
  if (nrow(Data) <= Chunk) {
    biglm(formula, data = Data)
  } else {
    FirstChunk <- Data[1:Chunk, ]
    Model <- biglm(formula, data = FirstChunk)
    for (i in seq(Chunk + 1, nrow(Data), by = Chunk)) {
      end <- min(i + Chunk - 1, nrow(Data))
      Model <- update(Model, Data[i:end, ])
    }
    Model
  }
}

# 過去10年間のCSVデータ読込み＆整形する関数
# 場所＝東京、条件＝良を基準(0)とする。
Cleaning_Data <- function(Cource) {
  AllData <- fread("2013-2023総合データ.csv")
  AllData <- AllData[!is.na(タイム) & タイム != 0 & !is.na(距離) & !is.na(条件) & !is.na(場所) & !is.na(コース) & 着順 != 0 & コース == Cource,]
  AllData[, 場所 := factor(場所, levels = c("東京", unique(場所[場所 != "東京"])))]
  AllData[, 条件 := factor(条件, levels = c("良", unique(条件[条件 != "良"])))]
  return(AllData)
}

# 過去10年間のCSVデータを、芝とダートの2種類に大別
AllData芝 <- Cleaning_Data("芝")
AllDataダ <- Cleaning_Data("ダ")

# 線形回帰モデルの式定義（目的変数=タイム、説明変数＝距離、条件、場所）
# 条件と場所の交互作用あり
formula <- as.formula("タイム ~ 距離 + 条件 * 場所")

# 距離（Short, Medium, Long）とコース(芝, ダート)、計６パターンのモデルを構築
芝Short_Model <- New_Model(AllData芝[距離 <= 1400], formula)
芝Medium_Model <- New_Model(AllData芝[距離 > 1400 & 距離 < 2100], formula)
芝long_Model <- New_Model(AllData芝[距離 >= 2100], formula)
ダShort_Model <- New_Model(AllDataダ[距離 <= 1400], formula)
ダMedium_Model <- New_Model(AllDataダ[距離 > 1400 & 距離 < 2100], formula)
ダlong_Model <- New_Model(AllDataダ[距離 >= 2100], formula)

# 構築したモデルを表示
summary(芝Short_Model)
summary(芝Medium_Model)
summary(芝long_Model)
summary(ダShort_Model)
summary(ダMedium_Model)
summary(ダlong_Model)

# ---------------（ここまでが過去10年間のデータを使ったモデル構築）
# ---------------（ここからが実際のレース出走馬の成績を使った期待値算出）

# CSV ファイルを読み込む関数
Sorting_CSV <- function(FileName) {
  InputData <- fread(FileName)
  list(
    Soted_ダShort = InputData[コース == "ダ" & 距離 <= 1400][, `:=`(
      場所 = factor(場所, levels = levels(AllDataダ$場所)),
      条件 = factor(条件, levels = levels(AllDataダ$条件))
    )],
    Soted_芝Short = InputData[コース == "芝" & 距離 <= 1400][, `:=`(
      場所 = factor(場所, levels = levels(AllData芝$場所)),
      条件 = factor(条件, levels = levels(AllData芝$条件))
    )],
    Soted_ダMedium = InputData[コース == "ダ" & 距離 > 1400 & 距離 < 2100][, `:=`(
      場所 = factor(場所, levels = levels(AllDataダ$場所)),
      条件 = factor(条件, levels = levels(AllDataダ$条件))
    )],
    Soted_芝Medium = InputData[コース == "芝" & 距離 > 1400 & 距離 < 2100][, `:=`(
      場所 = factor(場所, levels = levels(AllData芝$場所)),
      条件 = factor(条件, levels = levels(AllData芝$条件))
    )],
    Soted_ダLong = InputData[コース == "ダ" & 距離 >= 2100][, `:=`(
      場所 = factor(場所, levels = levels(AllDataダ$場所)),
      条件 = factor(条件, levels = levels(AllDataダ$条件))
    )],
    Soted_芝Long = InputData[コース == "芝" & 距離 >= 2100][, `:=`(
      場所 = factor(場所, levels = levels(AllData芝$場所)),
      条件 = factor(条件, levels = levels(AllData芝$条件))
    )]
  )
}

# 第一引数Dataを第二引数Modelに代入することで予測タイムを計算し、Dataの「予測タイム」列に追加する関数
Calc_ExpectedValue <- function(Data, Model) {
  if (nrow(Data) > 0) {
    coefficients <- coef(Model)
    切片 <- coefficients[1]
    距離指数 <- coefficients["距離"] * Data$距離
    条件指数 <- sapply(Data$条件, function(strCond) {
      if (strCond == "良") return(0) else return(coefficients[paste0("条件", strCond)])
    })
    場所指数 <- sapply(Data$場所, function(place) {
      if (place == "東京") return(0) else return(coefficients[paste0("場所", place)])
    })
    場所と条件の交互作用指数 <- mapply(function(strCond, place) {
      if (strCond == "良" || place == "東京") {
        return(0)
      } else {
        coeff_name <- paste0("条件", strCond, ":場所", place)
        if (coeff_name %in% names(coefficients)) {
          return(coefficients[coeff_name])
        } else {
          return(0)
        }
      }
    }, Data$条件, Data$場所)
    期待値 <- 切片 + 距離指数 + 条件指数 + 場所指数 + 場所と条件の交互作用指数
    Data$予測タイム <- 期待値
  } else {
    Data$予測タイム <- NA
  }
  return(Data)
}

# フォルダ内の全てのCSVファイルを取得
setwd("C:/Users/******/各馬のデータ")  #任意のフォルダパスを設定
CSVs <- list.files(pattern = "*.csv")

# 空のリストを作成
ExpectedValue_All_list <- list()

# CSVファイル毎に予測タイム(期待値)列を加えたデータを作成し、リストExpectedValue_All_listへ格納する
for (FileName in CSVs) {
  DataSet <- Sorting_CSV(FileName)
  ExpectedValue_ダShort <- Calc_ExpectedValue(DataSet$Soted_ダShort, ダShort_Model)
  ExpectedValue_芝Short <- Calc_ExpectedValue(DataSet$Soted_芝Short, 芝Short_Model)
  ExpectedValue_ダMedium <- Calc_ExpectedValue(DataSet$Soted_ダMedium, ダMedium_Model)
  ExpectedValue_芝Medium <- Calc_ExpectedValue(DataSet$Soted_芝Medium, 芝Medium_Model)
  ExpectedValue_ダLong <- Calc_ExpectedValue(DataSet$Soted_ダLong, ダlong_Model)
  ExpectedValue_芝Long <- Calc_ExpectedValue(DataSet$Soted_芝Long, 芝long_Model)

  ExpectedValue_All <- rbind(
  ExpectedValue_ダShort,
  ExpectedValue_芝Short,
  ExpectedValue_ダMedium,
  ExpectedValue_芝Medium,
  ExpectedValue_ダLong,
  ExpectedValue_芝Long
  )
  ExpectedValue_All_list[[FileName]] <- ExpectedValue_All
}

# リストExpectedValue_All_listの中身を表示
for (FileName in CSVs) {
  cat("\nResults for", FileName, ":\n")
  print(ExpectedValue_All_list[[FileName]])
}

# ディレクトリを設定（もとに戻す）
setwd("C:/Users/******")

# ---------------（ここからが各馬の成績と期待値の乖離具合を分析する処理）

# 各レース毎の残差（タイム－予測タイム）、各馬毎の統計量（平均残差・標準偏差）を計算する関数
# NAがない行で残差を計算
Calc_Residuals <- function(Predictions, HorseName) {
  Predictions <- Predictions[!is.na(タイム) & !is.na(予測タイム), 残差 := タイム - 予測タイム]
  # 馬名と統計量を含むデータフレームを作成
  data.table(
    馬名 = HorseName,
    平均残差 = mean(Predictions$残差, na.rm = TRUE),
    標準偏差 = sd(Predictions$残差, na.rm = TRUE)
  )
}

# リストの各要素（各馬のデータ）に対してCalc_Residualsを呼び出して、残差の統計量を取得する関数
AllHorsePerformance <- lapply(names(ExpectedValue_All_list), function(name) {
  HorseName <- gsub(".csv", "", name)
  Calc_Residuals(ExpectedValue_All_list[[name]], HorseName)
})

# 各馬のデータを縦に連結（行を追加する形で結合）し、平均残差で降順に並び替え
FinalPerformance <- rbindlist(AllHorsePerformance)
setorder(FinalPerformance, -平均残差)
print(FinalPerformance)

# ---------------（ここからが乖離具合を視覚化する処理）

# 必要なライブラリをロード
packages <- c("ggplot2")
for (pkg in packages) {
  if (!require(pkg, character.only = TRUE)) {
    install.packages(pkg)
    library(pkg, character.only = TRUE)
  }
}

# ggplotを使用してデータを視覚化
ggplot(FinalPerformance, aes(x = reorder(馬名, 平均残差), y = 平均残差, fill = 馬名)) +
  geom_col(show.legend = FALSE) +  # 棒グラフ、凡例非表示
  geom_errorbar(aes(ymin = 平均残差 - 標準偏差, ymax = 平均残差 + 標準偏差), width = .2, color = "black") +  # エラーバー
  geom_text(aes(label = sprintf("%.2f", 平均残差)), position = position_dodge(width = 0.9), vjust = -0.5, size = 3, color = "black") +  # ラベルの追加
  labs(title = "馬別の平均残差と標準偏差", x = "馬名", y = "平均残差") +
  theme_minimal() +
  theme(axis_text_x = element_text(angle = 90, hjust = 1),  # X軸のラベルを縦に表示
        axis_title = element_text(size = 12),  # 軸ラベルのフォントサイズ
        plot_title = element_text(size = 14, face = "bold"))  # タイトルのフォント設定

おまけ１

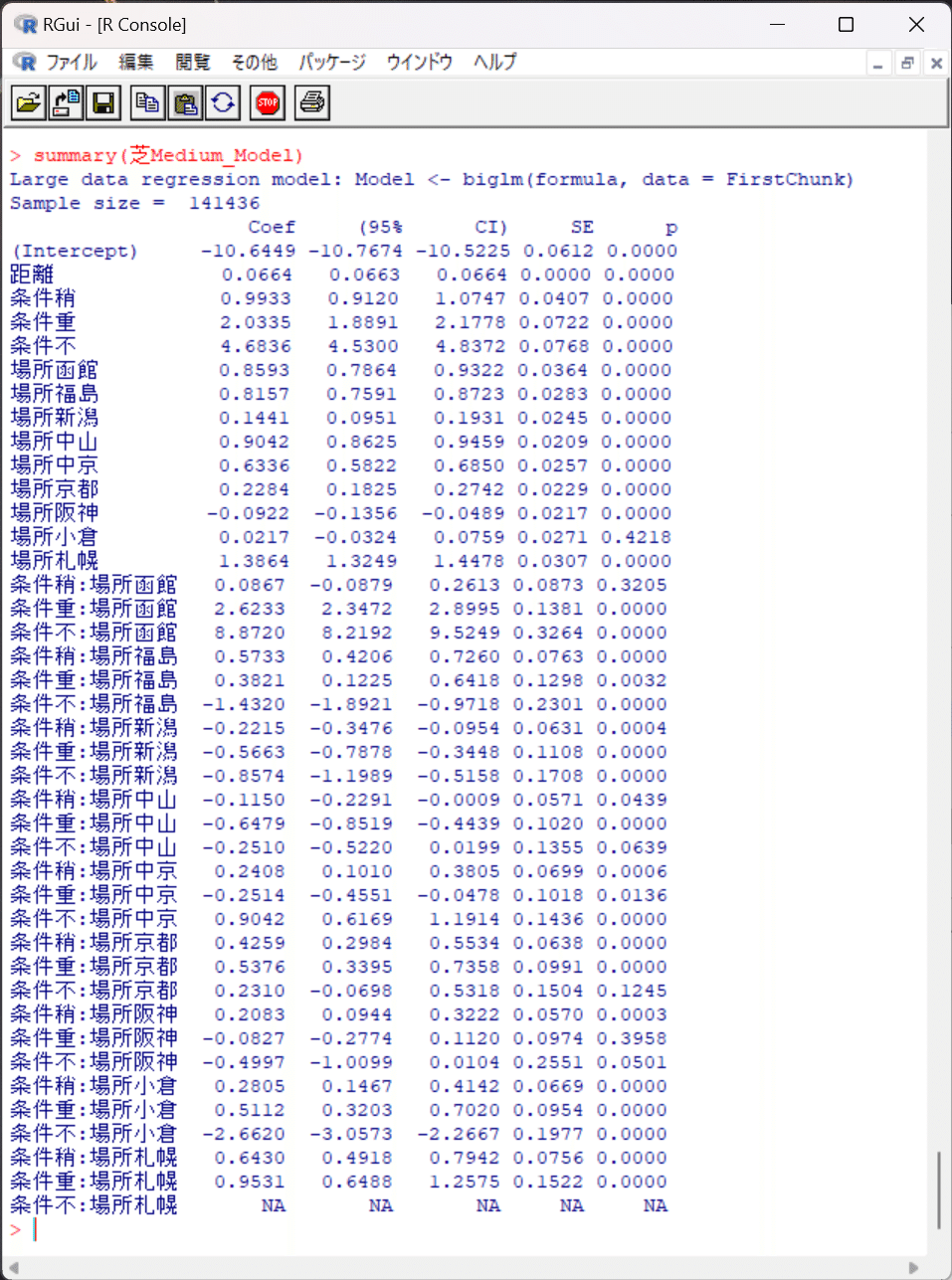
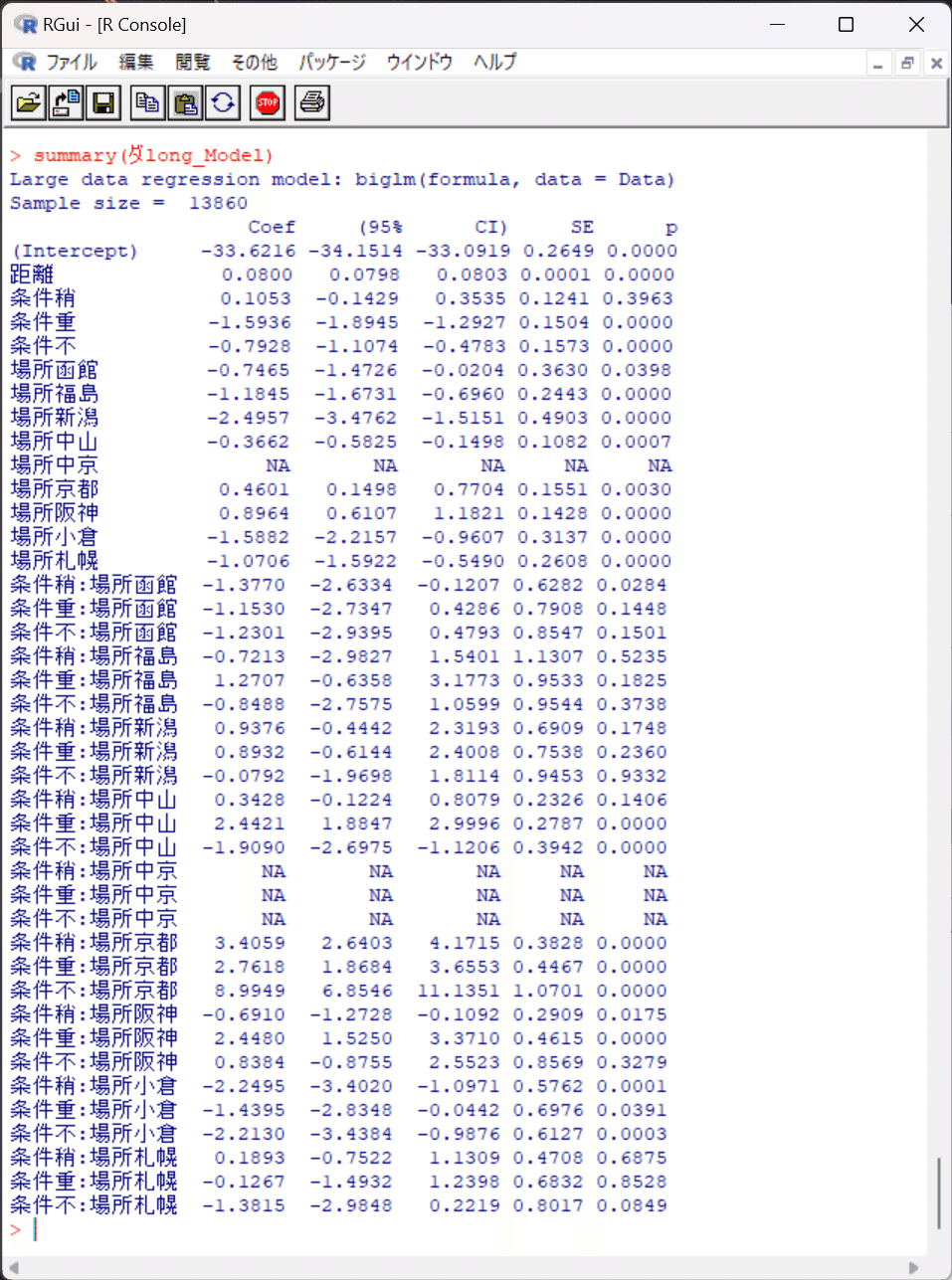
今回作成した6つの線形回帰モデルのサマリーを貼り付けます。
これを見れば切片と各回帰係数が分かるので、VBAなどの他言語に回帰式を移植できますね。予測データから各説明変数Xを抽出して回帰式に代入すれば期待値（予測タイム）が得られますし、予測タイムと実測タイムの残差も単純計算なので、が、他言語でも簡単に実装できると思います。

おまけ２

線形回帰モデルでは回帰式を明示的に得られたので使い勝手が良かったのですが、もっと予測精度を高めたい場合は他のアプローチが考えられます。機械学習（統計学の一部）の手法で大量のデータから複数の決定木モデルを組み合わせる勾配ブ―スティングを使う方法など。
この方法では残念ながら回帰式を明示的に得られないので、他言語への移植が出来ないのが難点です。
同じように「距離」「条件」「場所」（条件と場所の交互作用有）で勾配ブ―スティングをRにさせる場合のコードです。

packages <- c("data.table", "xgboost")
for (pkg in packages) {
  if (!require(pkg, character.only = TRUE)) {
    install.packages(pkg)
    library(pkg, character.only = TRUE)
  }
}

# CSVファイルをdata.table型で読込む
# カテゴリ変数をダミー変数に変換
data <- fread("2013-2023総合データ.csv")
data <- data[!is.na(タイム) & タイム != 0 & !is.na(距離) & !is.na(条件) & !is.na(場所) & !is.na(コース) & 着順 != 0,]
data$条件 <- as.factor(data$条件)
data$場所 <- as.factor(data$場所)

# タイムをlabels変数に保存
labels <- data$タイム

# matrix型に変換（-1で切片を除外）
data <- model.matrix(~ 距離 + 条件 * 場所 - 1, data)

# データセットを分割
train_index <- sample(1:nrow(data), 0.8 * nrow(data))
train_data <- data[train_index,]
train_labels <- labels[train_index]
test_data <- data[-train_index,]
test_labels <- labels[-train_index]

# モデルの訓練
dtrain <- xgb.DMatrix(data = train_data, label = train_labels)
dtest <- xgb.DMatrix(data = test_data, label = test_labels)

# パラメータ設定
params <- list(
  booster = "gbtree",
  objective = "reg:squarederror",
  eta = *,
  gamma = *,
  max_depth = *,
  min_child_weight = *,
  subsample = *,
  colsample_bytree = *
)

# モデルの訓練
xgb_model <- xgb.train(
  params = params,
  data = dtrain,
  nrounds = *,
  watchlist = list(eval = dtest, train = dtrain),
  print_every_n = *,
  early_stopping_rounds = *,
  maximize = FALSE
)

# モデルの評価
preds <- predict(xgb_model, dtest)
rmse <- sqrt(mean((preds - test_labels)^2))
print(rmse)

※パラメータは適当に変更してチューニングしてください。

あとは実際のレース情報（各馬の過去競争成績）から情報を抽出して、作成したモデルへ代入し、期待値を計算。期待値と実測タイムの残差を馬ごとに計算して優劣を判断するという流れは同じです。
ただし代入するデータはmatrix型にしてモデル構築時のデータセットと同じ形式にしておく必要があります。

勾配ブ―スティング法を使った方法は、後日別記事で紹介予定です。

2024/12/8追記
勾配ブ―スティング法を使った予測方法を書いたので、追記しておきます。
統計学的アプローチによる競馬予想（勾配ブースティング＆アンサンブル編）｜地獄の油揚げ