見出し画像

統計学的アプローチによる競馬予想（勾配ブースティング＆アンサンブル編）

地獄の油揚げ

前回はシンプルな「線形回帰モデル」を考えましたが、今回は予測精度を重視した方法を考えます。

「勾配ブースティング」という機械学習手法で過去10年間のレース情報を分析し、馬ごとの着順期待値（0～1の間に変換した着順の期待値）を直接求めることで順位予想します。
また、複数のモデルを組合せて精度UPを図るアンサンブルも行います。
勾配ブ―スティングやアンサンブルは分析コンペでも採用実績の高い手法です。

ここでは、統計ソフト「R」を使います。
Rのインストールは必要ですが、ここで紹介するコードはコピペで実践投入できるので、Rや統計学の知識が無くても大丈夫です。
（結論だけ知りたい人は★マークの項目のみ参照ください）


【概要説明】

全体像

全体の流れはこちら。大項目４つに分けて考えます。

1.事前準備
1-1 統計ソフトRをインストールする。
1-2 学習データ準備する。
　JRA-VANを使って過去10年間のJRAレース情報をダウンロード。

2.モデル構築
2-1 学習データを使ってGBDTモデル構築。
　「着順指数」を目的変数とした回帰モデル。
2-2 学習データを使ってGBDTモデル構築。
　「予測タイム」を目的変数とした回帰モデル。
2-3 学習データを使ってGBDTモデル構築。
　オッズに関するアノマリーを考慮した回帰モデル。

3.期待値を計算
3-1 テストデータ（予測したいレース情報）をWebから自動取得。
　指定したURL（netkeiba）をRでスクレイピング。
3-2 テストデータをモデルへ代入し、予測値を計算。

4.アンサンブル処理
4-1 上記2で作成した３つのモデルを1つに統合する。
　3つのモデルの予測値を使って、更に「2層目」のGBDTモデル構築。
　馬ごとの最終スコア（2層目モデルの予測値）を見比べて順位予測。

使用イメージ

いくつか予測例（画像左側）と実際の結果（画像右側）を貼り付けます。
こんな感じで結果が得られますよ、というイメージです。

実行例１
実行例２
実行例３

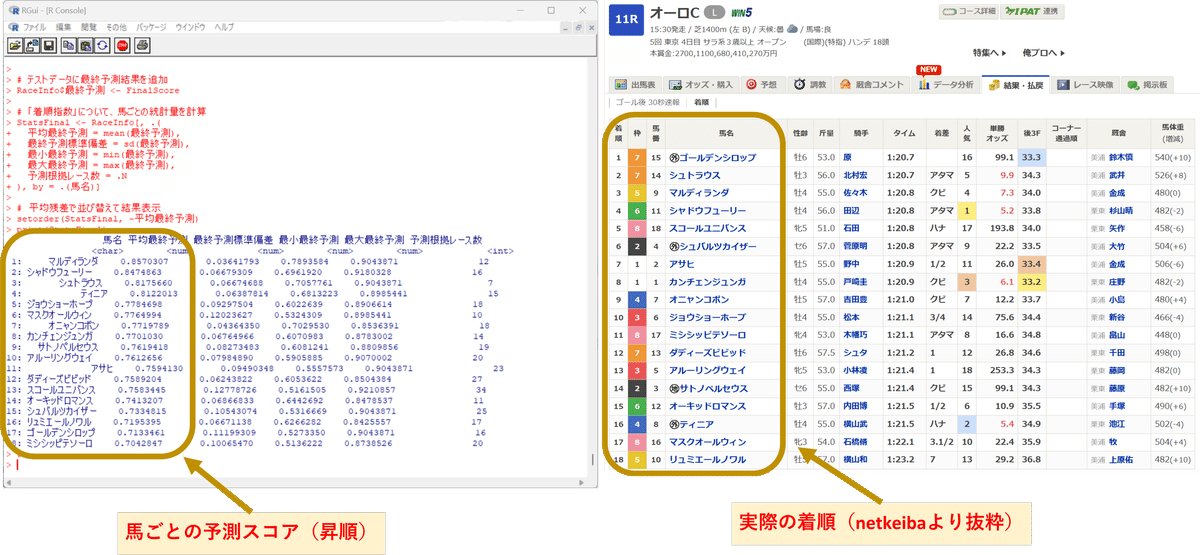
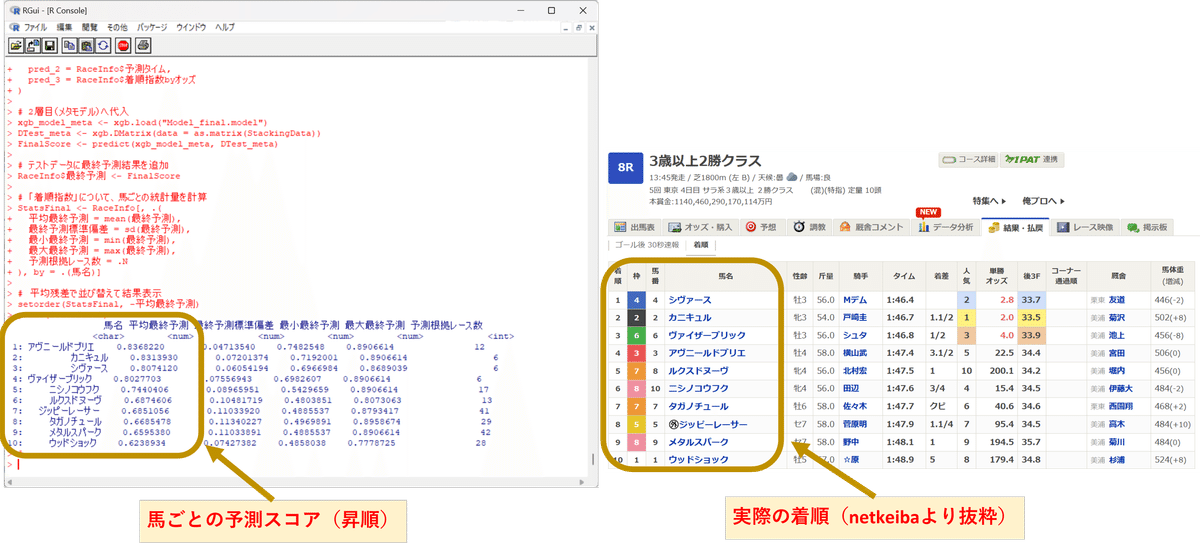
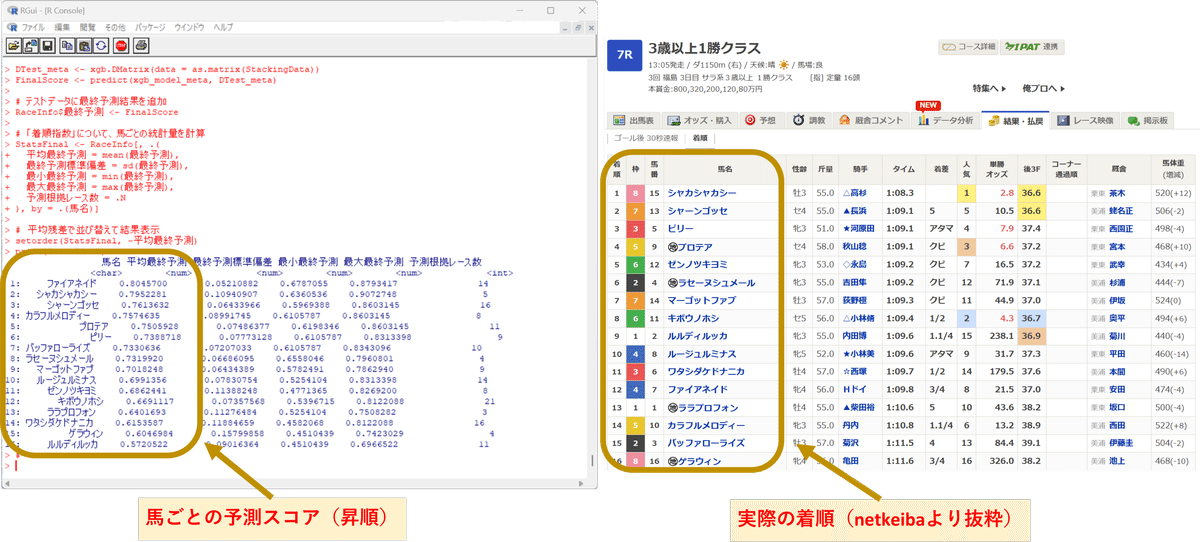
執筆にあたり無作為にピックアップして予測したレースなので、良い例ではないかもしれません。上記例ではどれも１着は外していますが、上位３頭の傾向は大体合っているかなと思います。
（競馬なので絶対はありませんが、少なくとも判断材料の１つにはなると思います。）

【動作確認済み環境】
・Windows 11 Home (64bit)
・CPU：Intel Core i5）
・メモリ：16GB
以上、導入部分おわり。
ここから本編です。

【事前準備】

まずは、下準備です。

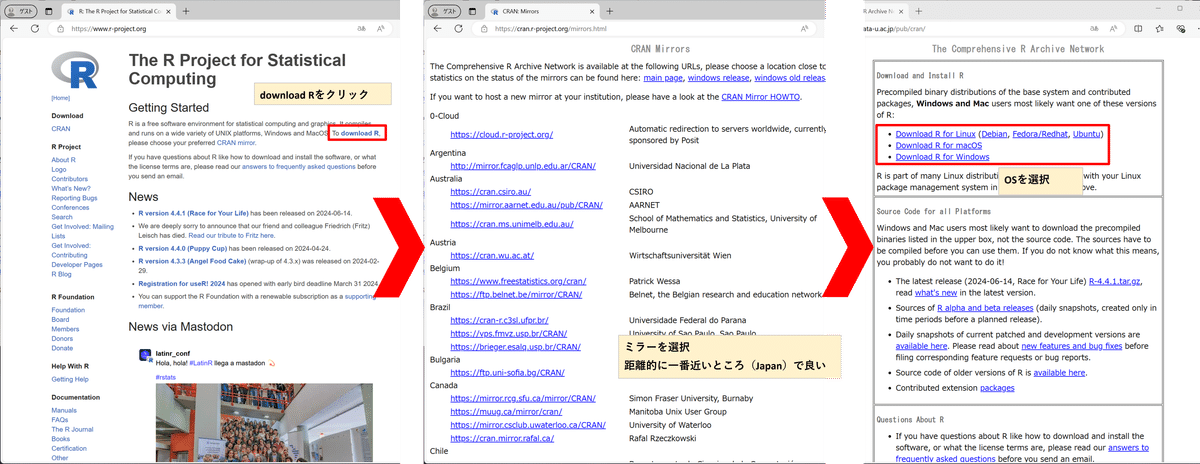
★統計ソフト「R」のインストール手順

RをWebサイトからダウンロードしてください。
※医学・心理学などの研究分野でも広く使われているフリーソフトです。

RのWebページから最新版をDL

無事インストールできたら、Rを立ち上げます。
起動画面はこんな感じ。

Rの起動画面

初回起動時は、「ファイル＞ディレクトリの変更」を選択し、ディレクトリ（任意の作業フォルダ）を設定します。
※ディレクトリを設定しておくと、ファイル読込時にフルパスを指定する必要が無くなる等、スムーズに進められます。

続いて、以下コードをRで実行（R画面上にコピペ）し、今回の分析に必要なパッケージを全部DLしておきましょう。

install.packages("bit64")
install.packages("data.table")
install.packages("xgboost")
install.packages("stringi")
install.packages("httr")
install.packages("rvest")

実行するとミラー選択画面が現れるので、適当に選択して進めてください。
ミラー選択後、自動的にパッケージのインストールが始まります。

Rのミラー選択画面

これでRのセットアップは完了。

★学習データの準備（JRA-VANを使ってCSVファイル取得）

続いて、学習データ（過去10年間のJRAレース情報）を準備します。
JRA-VANのTARGET frontier JVをインストールして、直近10年間のレース情報（約54万件）をCSV形式でダウンロードしましょう。
※本来は有料サービスですが、最初の1か月は無料体験期間があります。
　必要な学習データさえダウンロードしたらもう用済みなので、すぐ解約＆アンインストールしても構いません。
胴元が提供する公式データなだけあって、細かな情報まで得られます。

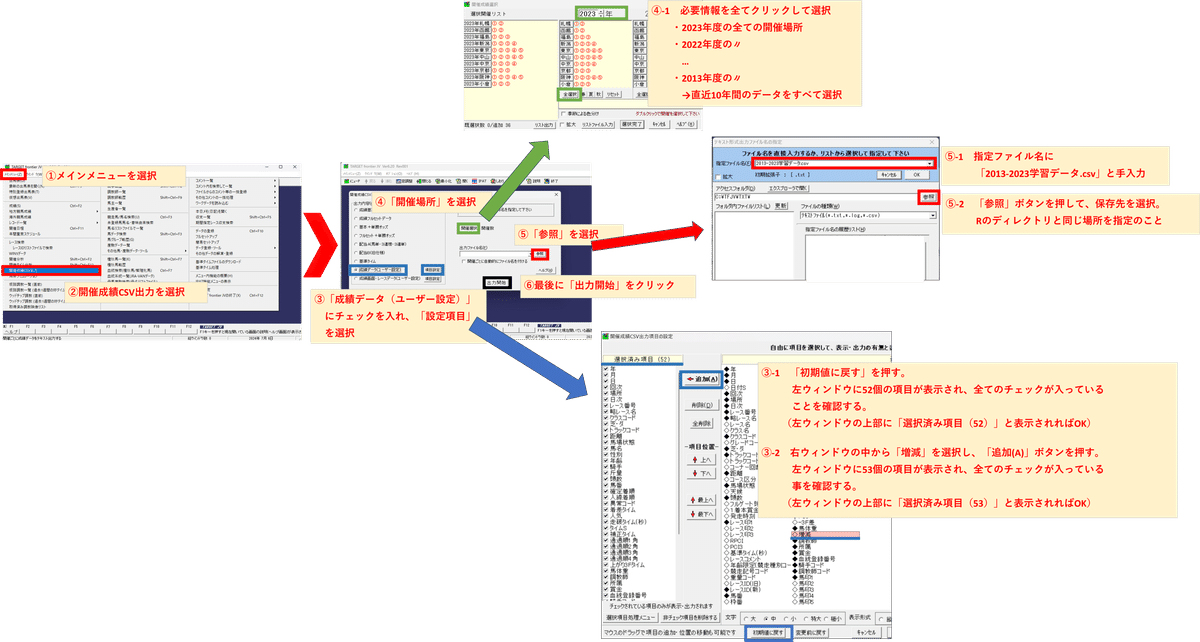
TARGET frontier JVの操作手順（CSVデータのダウンロード）

上画像の手順で、最後に「出力開始」をクリックするとダウンロードが始まります。
※通信環境にも依りますが、ダウンロードに20分くらい掛かります。
ファイル名は「2013-2023学習データ.csv」とします。

続いて、ダウンロードしたCSVファイルにヘッダー（見出し行）を追加します。CSVファイルをメモ帳で開き、先頭部分にヘッダーを挿入して下さい。
※エクスプローラー上で「右クリック＞プログラムから開く＞メモ帳」でCSVファイルを編集できます。

CSVファイルにヘッダー（見出し行）を挿入する

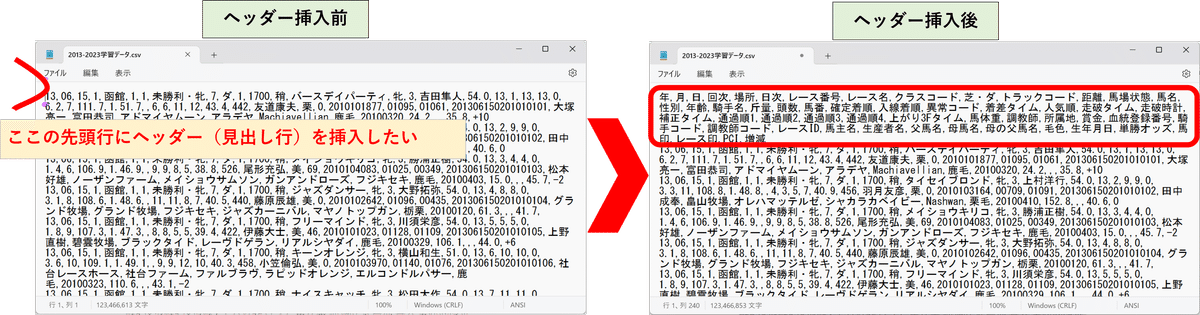
なおヘッダーに挿入する文字列は、以下をコピペして活用ください。
--------------
年,月,日,回次,場所,日次,レース番号,レース名,クラスコード,芝ダ,トラックコード,距離,馬場状態,馬名,性別,年齢,騎手名,斤量,頭数,馬番,確定着順,入線着順,異常コード,着差タイム,人気順,走破タイム,走破時計,補正タイム,通過順1,通過順2,通過順3,通過順4,上がり3Fタイム,馬体重,調教師,所属地,賞金,血統登録番号,騎手コード,調教師コード,レースID,馬主名,生産者名,父馬名,母馬名,母の父馬名,毛色,生年月日,単勝オッズ,馬印,レース印,PCI,増減
--------------

CSVファイルは、文字コードUTF-8で保存します。
※メモ帳の「名前を付けて保存＞エンコード欄『UTF-8』または『UTF-8(BOM付き)』を選択＞保存」で文字コードを変更可能。『ANSI』はダメ。
※ExcelでCSVファイルを開いた場合は、「名前を付けて保存＞ファイル種類欄『CSV UTF-8（コンマ区切り）（*.csv）』>保存」で文字コードを変更可能。『CSV（コンマ区切り）（*.csv）』はダメ。

これで学習データの準備は完了。


【モデル構築】

ここからは若干理屈っぽくなりますが、競馬予想の考え方とチューニング方法です。

勾配ブ―スティングの特徴

勾配ブ―スティングは、複数の学習器を組み合わせて一つの強力な予測モデルを構築する方法です。学習器による予測を行い、その予測で生じた誤差を修正するように次の学習器が作られていくことで、連続的に学習器が積み重なり全体精度が上がります。
特に、学習器が決定木であるものを指してGBDT（Gradient Boosting Decision Trees）と呼びます。決定木というのは、複数の条件に基づいてデータを繰り返し分割していくプロセスです。Yes/Noの二分岐で答えを絞っていく言葉遊びゲーム（20 Questions）を連想するとイメージしやすいかもしれません。

今回使うGBDTですが、選択肢（＝ノード）が集まって決定木を構築し、決定木による予想の誤差を修正する形で次の決定木が作られるのが特徴です。そのため、データの非線形的な特徴を捉えることが出来ますし、特徴量の相互作用も自動的に学習出来ます。つまり、競馬予想のような複雑なデータセットを分析するのに適しています。
GBDTを実装するにはXGBoost、LightGBM、CatBoostといったRのパッケージを読込んで使います。以下、XGBoostパッケージを使って実装します。

XGBoostの「booster」パラメータ項目のうち、gbtreeを選択することで学習アルゴリズムにGBDTを設定できます。

boosterパラメータの設定

タスクについて

タスクとは、予測モデルが解決しようとしている問題の種類を指します。まずは問題の捉え方というべきか、GBDT予測モデルを使って何を解決したいのかを明確にします。
単勝狙いの買い方ならば「1着になる確率が知りたい」でしょうし、複勝狙いならば「3着以内に入るか、それ以外になるかを分類したい」というニーズでしょう。一口に競馬予想と言っても、どんなタスクが最適かは状況次第です。

代表的なタスクとしては…
回帰タスク：連続値を予測する問題。
　ex.不動産価格や株価の予想など。
分類タスク：データがどのカテゴリに属するかを予測する問題。
　ex.二値分類（スパムメール判別）や多クラス分類（文字認識）など。
ランキングタスク：データの順位付けを行う問題。
　ex.ユーザー履歴に基づくWeb広告や検索エンジンの候補予測など。

実際には、もっと細かく細分化したタスクをXGBoostの「objective」パラメータ項目に設定します。

objectiveパラメータの設定

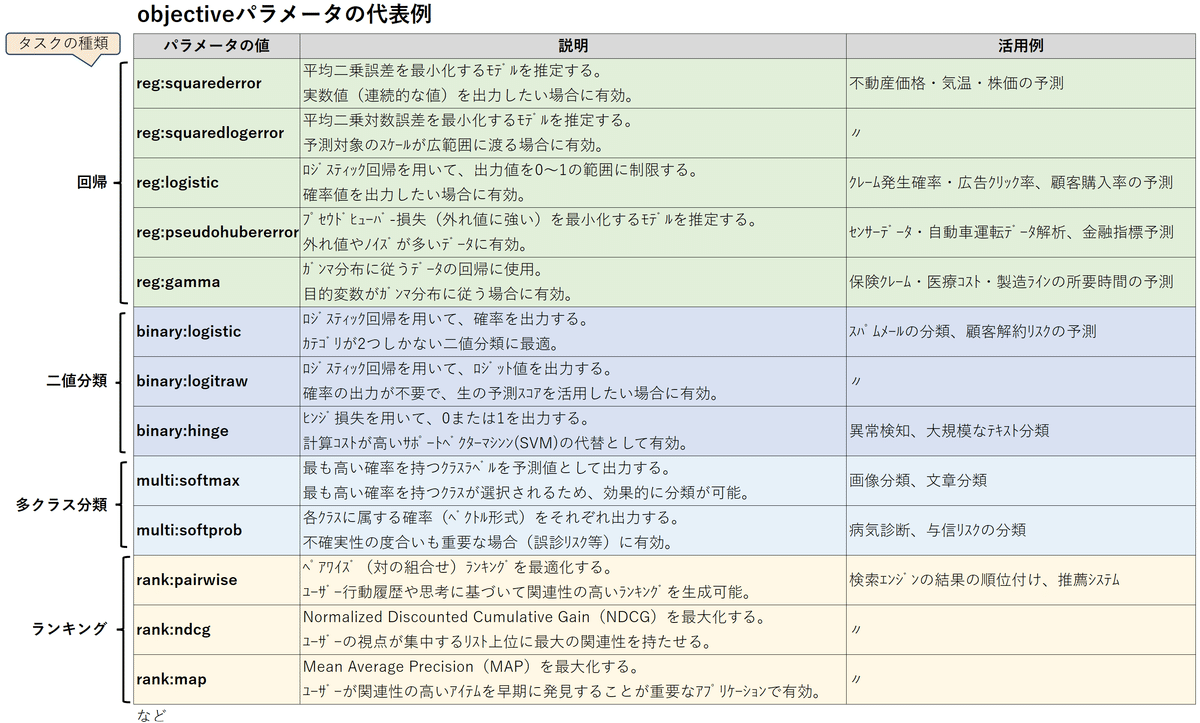
素直に考えるならば、順位の期待値を算出できるreg:squarederror（回帰）か、○位以内に入る確率を算出できるbinary:logistic（分類）が有力候補になるでしょう。

ハイパーパラメータについて

ハイパーパラメータには、GBDT予測モデルの構造・学習速度・複雑さなどを制御する役割があります。適切なハイパーパラメータ―の値を見つけてチューニングすることで、モデルの予測精度・汎化性UPが狙えます。
手動でチューニングする場合は、最初にざっくりと（経験的に良さげな値や先行研究から得た値を）設定したあと、各パラメータを弄っていき評価指標の改善度合いを確認します。パラメータによって重要度が異なるので、重要なパラメータから弄っていきます。
自動でチューニングする場合は、クロスバリデーションやランダムサーチなどを使って、最も良い評価指標が得られるパラメータの組合せを求めて設定します。
それぞれのパラメータの特徴とチューニング例をまとめました。

GBDTモデルの学習設定パラメータ

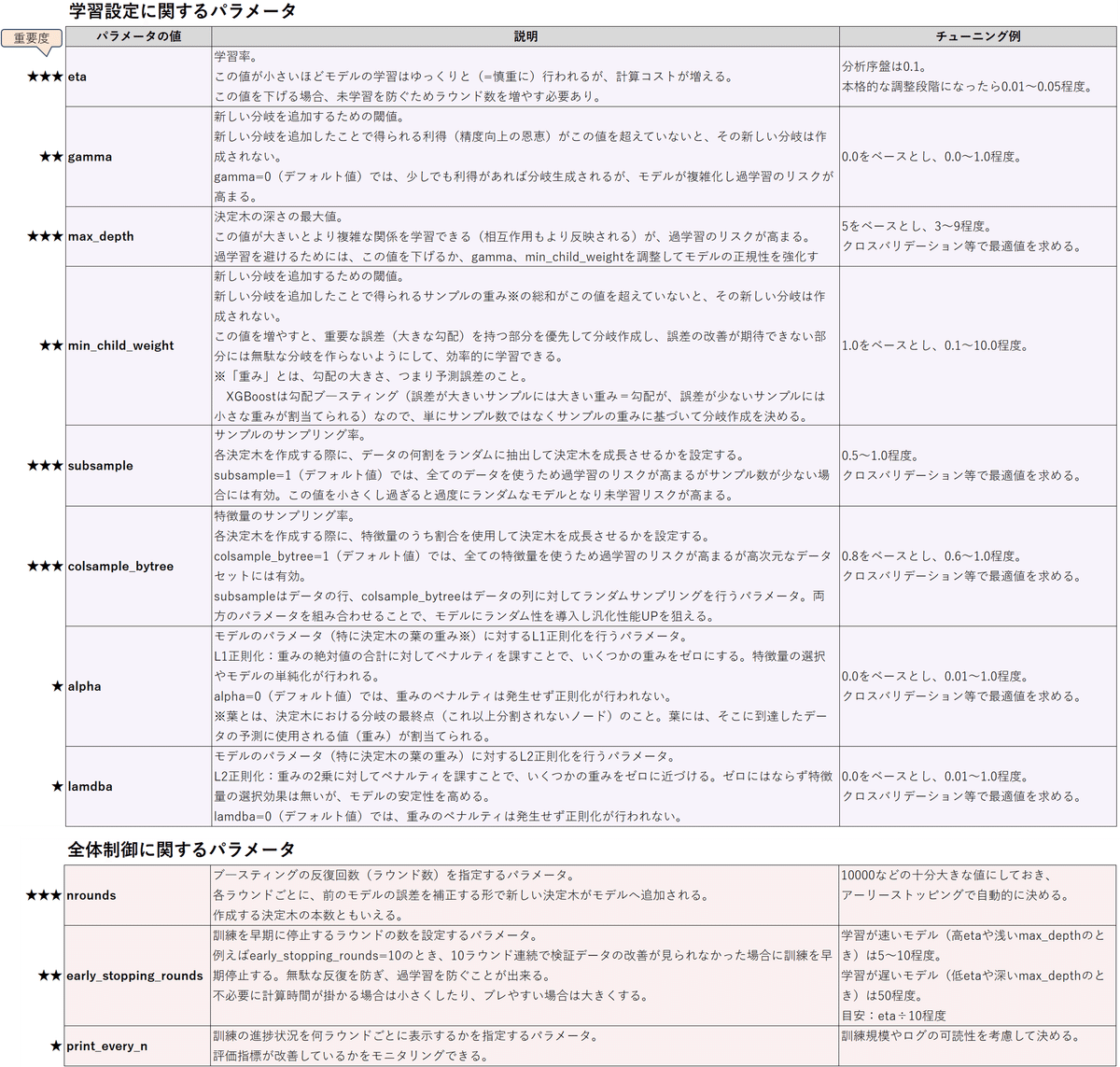
細かく書きましたが、この辺は後で調整すれば良いです。
正直パラメータのチューニングよりも、説明変数の見極めの方が重要だと思います。

学習データの前処理

先ほど「タスクについて」の部分でも触れましたが、一口に競馬予想といってもどんな予測出力に価値があるかは考え方や状況次第です。
ここでは、出走馬それぞれの強さ（具体的には着順に結び付く強さを指す）を数値化する回帰モデルを組立ててみます。

この前提であれば、回帰モデルの目的変数（つまりモデルの出力値）には、「着順に関する何らかの期待値」を設定することが自然な発想でしょう。では、これをどう定義するか…。
学習データに含まれる「確定着順」の値をそのまま使ってしまうと、レース規模に対する重みがバラバラなので不適切です。
※例えば同じ10位でも、10頭立てレースにおける10位と18頭立てレースにおける10位では重みが異なります。
そこで、レース規模に応じて「確定着順」を0～1の範囲に変換（正規化）して、重みを均一化して扱います。
以下は4つの計算方法で正規化を試みた結果です。

確定着順を0〜1の範囲に変換する方法4つ

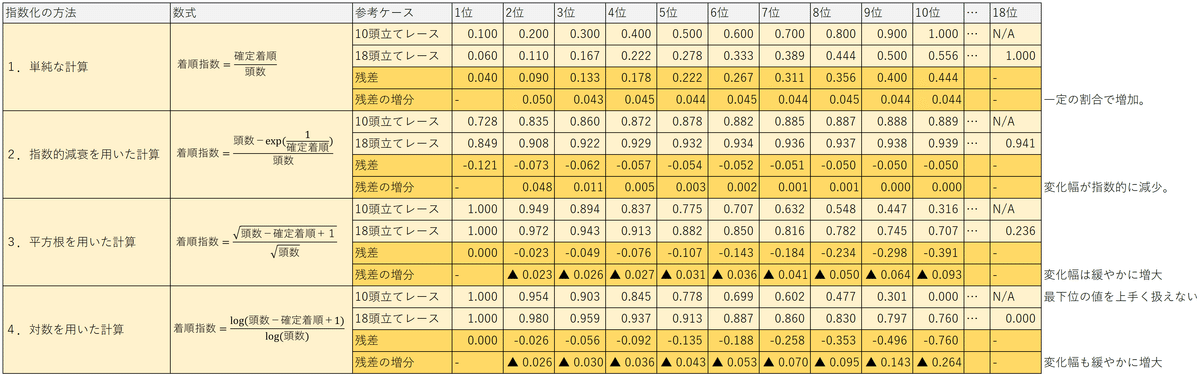
方法１は、単純に「確定着順」を「頭数」で割ったもの。
方法２は、指数的減衰を用いた計算。
方法３は、平方根を用いた計算。
方法４は、対数を用いた計算。
→方法１はレース規模によるバラつきが大きく、方法４は最下位を上手く表現できないため不適切と判断。一方で、方法２と方法３はどちらもレース規模に応じて緩やかな重み付けが出来ています。また、どちらかと言うと指数の取りうる範囲が広い方法３の方が使い勝手が良いと判断。

結論として方法3による正規化を採用し、これを便宜上、着順指数と呼ぶことにします。
目的変数である「着順に関する何らかの期待値」には、この着順指数の値を当てはめれば丁度良さそうですね。

学習データから着順指数を求める処理をRで書くと…

# パッケージ読込み
library(bit64)
library(data.table)
library(xgboost)

# 着順指数を計算する関数を定義（平方根を使用した算出法）
Calc_RankIndex <- function(Rank, TotalCnt) {
 着順指数 <- sqrt(TotalCnt - Rank + 1) / sqrt(TotalCnt)
 return(着順指数)
}

# 学習データのCSVファイルを読込んで、新しい列として着順指数を追加
JRAdata <- fread("2013-2023学習データ.csv", encoding = "UTF-8")
JRAdata$着順指数 <- mapply(Calc_RankIndex, JRAdata$確定着順, JRAdata$頭数)

Calc_RankIndexの部分が、方法3の計算式にあたります。
これを実行すると、生の学習データを格納した変数JRAdataへ新たに「着順指数」という列が追加されます。

ついでに、学習データ内の欠損値を取り除きたい場合は、こんな感じで書き加えます。

# 着順指数を追加する処理
（前述同様のため省略）
#-----

JRAdata <- JRAdata[
 確定着順 != 0 &
 走破タイム != 0 &
 !is.na(着順指数) &
 !is.na(走破タイム) &
 !is.na(距離) &
 !is.na(馬場状態) &
 !is.na(場所) &
 !is.na(月) &
 !is.na(芝ダ) &
 !is.na(馬体重) &
 !is.na(増減) &
 !is.na(騎手名) &
 !is.na(馬番) &
 !is.na(レース番号) &
 !is.na(単勝オッズ)
,]

これで、分析に使う学習データの形が整えられました。
（ちなみに、分析に使う項目情報のことを「特徴量」と呼びます）

このように、新たな特徴量を追加したりノイズを取り除いたりと、生の学習データを適切な形に整えるプロセスを前処理といいます。生データをそのまま目的変数や説明変数に使うよりも、前処理を挟んだデータの方が特徴をよく捉えられ、精度UPに繋がります。
※余談ですが、新たな特徴量を追加する場合、特にGBDTでは加減よりも乗除の計算を加えてあげた方がより効果的です。(乗除の前処理の例：1人辺り●●消費量、単位面積辺り単価など）

説明変数について

ここまでで、「回帰タスクであること」「目的変数が着順指数であること」という２つの方針が決まり、モデルの形が見えてきました。続いて、目的変数に影響を与える要因（＝説明変数）を考えます。

説明変数をどうやって決めるかは悩みどころですが、前提として、予測モデルの構成に使うデータ（学習データ）の項目と、予測モデルへ代入するデータ（テストデータ）の項目は揃える必要があります。
つまり学習データとテストデータに共通する項目の中から説明変数を選ぶことになります。
※テストデータについては詳細後述しますが、今回「ランニングコスト無料」に拘ったため、学習データとテストデータの情報源をそれぞれ分けざるを得ませんでした。そのため得られる情報の項目に不一致が生じています。詳細は次の通り。

学習データとテストデータに共通して含まれる項目

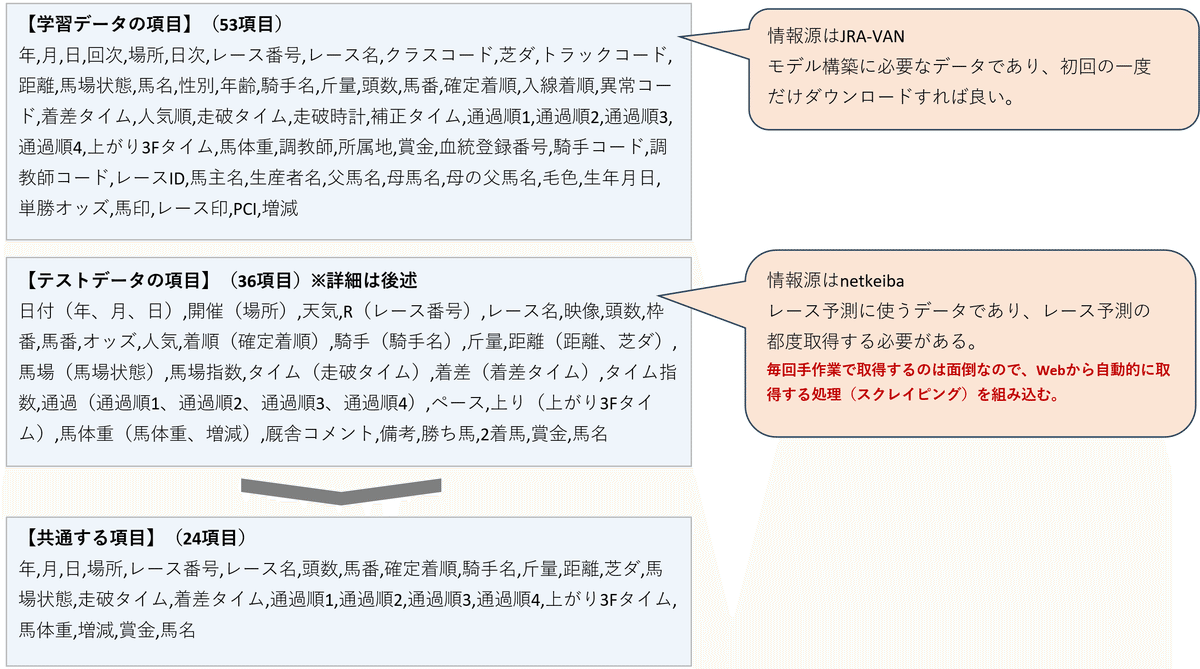
こうした事情から、説明変数として採用し得る選択肢は24項目です。
ここでの目的変数は「着順指数」なので、着順に強い影響を与える項目はどれかという視点で更に候補を絞ります。明らかに関係ない項目や目的変数に組込まれるている項目や重複項目を排除すると..。
「月」「場所」「馬番」「騎手名」「距離」「芝ダ」「馬場状態」「馬体重」「増減」の9項目に絞られました。
※9項目の考え方については、以下の通り。

各説明変数の扱い方

なおカテゴリカル変数として扱う特徴量は、そのままだとRでうまく処理できないため、各レベルを明示してfactor型へ変換しておきます。
量的変数として扱う特徴量は、特に変換せずそのまま使います。

# 学習データの前処理
（前述同様のため省略）
#-----

# カテゴリカル変数「芝ダ」「馬場状態」「場所」「月」「馬番」を変換
JRAdata$芝ダ <- factor(JRAdata$芝ダ, levels = c("芝", "ダ"))
JRAdata$馬場状態 <- factor(JRAdata$馬場状態, levels = c("重", "不", "良", "稍"))
JRAdata$場所 <- factor(JRAdata$場所, levels = c("京都", "阪神", "札幌", "小倉", "新潟", "中京", "中山", "東京", "函館", "福島"))
JRAdata$月 <- factor(JRAdata$月, levels = as.character(1:12))
JRAdata$馬番 <- factor(JRAdata$馬番, levels = as.character(1:18))

# カテゴリカル変数「騎手名」を変換
# 出場回数100回以上の場合はそのまま、未満の場合は"Othre"に仕分ける
Ride_Cnt <- table(JRAdata$騎手名)
Frequent_JockeyName <- unique(names(Ride_Cnt[Ride_Cnt >= 100]))
JRAdata$騎手名 <- ifelse(JRAdata$騎手名 %in% Frequent_JockeyName, JRAdata$騎手名, "Other")
JRAdata$騎手名 <- factor(JRAdata$騎手名)

# カテゴリカル変数「距離」を変換
JRAdata$距離カテゴリ <- cut(JRAdata$距離, breaks = c(-Inf, 1400, 2000, 3000, Inf), labels = c("短距離", "中距離", "長距離", "超長距離"), right = TRUE)

これで9項目の特徴量を扱う準備が整いました。
ただし、9項目全てを（説明変数として）採用するかどうかは、更に検証が必要です。モデルの複雑さや説明に筋が通るか等のポイントも考慮し、最終的には人間の頭で考えて決めます。
少し話が逸れますが、9項目の特徴量に関する検証例を2つほど紹介します。
※あくまで参考ですが、判断材料の足しにはなるかと…

　【9項目の特徴量に関する検証例①】
L1正規化を通して説明変数の重要度を確認する例です。
1正則化には不要な説明変数の係数を減少させる（あるいはゼロにする）性質があるので、これを利用して予測に寄与していない説明変数を炙り出すことができます。L1正則化ありの回帰分析（＝Lasso回帰）を行い、その結果、係数値が0になった説明変数を見つけたら「大して役に立たない項目」だったと判断できます。
※正則化とは、簡単に言うとモデルの複雑さに応じてペナルティを課すもの。詳細は前述の「ハイパーパラメータ―について」の項目参照。
ハイパーパラメータ―alphaの値を調整することでL1正則化を適用できます。

# 学習データの前処理
（省略）
#-----

# カテゴリカル変数を変換
（省略）
#-----

# 線形回帰モデルを作成（L1正則化あり＝Lasso回帰を実行）
# 目的変数：「着順指数」
# 説明変数：「距離カテゴリ」「増減」「馬体重」「場所」「馬番」「芝ダ」「馬場状態」「月」「騎手名」
library(glmnet)
Labels <- JRAdata$着順指数
MatrixData <- model.matrix(~ 距離カテゴリ + 増減 + 馬体重 + 場所 + 馬番 + 芝ダ + 馬場状態 + 月 + 騎手名 - 1, JRAdata)
CV_Lasso <- cv.glmnet(MatrixData, labels, alpha = 1)　#alpha=1でL1正則化あり
Lambda <- CV_Lasso$lambda.min * 5  # L1正則化のペナルティを意図的に強めたいので5倍する
Lasso_Model <- glmnet(MatrixData, Labels, alpha = 1, lambda = Lambda)

# モデルの係数を取得し、有効な（係数がゼロでない）説明変数のみを表示
Coef_Lasso <- coef(Lasso_Model)
Coef_Valid <- which(Coef_Lasso != 0)
Valid_Names <- rownames(Coef_Lasso)[Coef_Valid]
Valid_Coefficients <- as.numeric(Coef_Lasso[Coef_Valid])

# 説明変数の係数を変数ごとに表示
for (i in 1:length(Valid_Names)) {
  cat(Valid_Names[i], ":", Valid_Coefficients[i], "\n")
}

glmnetパッケージを使って直線回帰モデルを作り、L1正則化をすると…

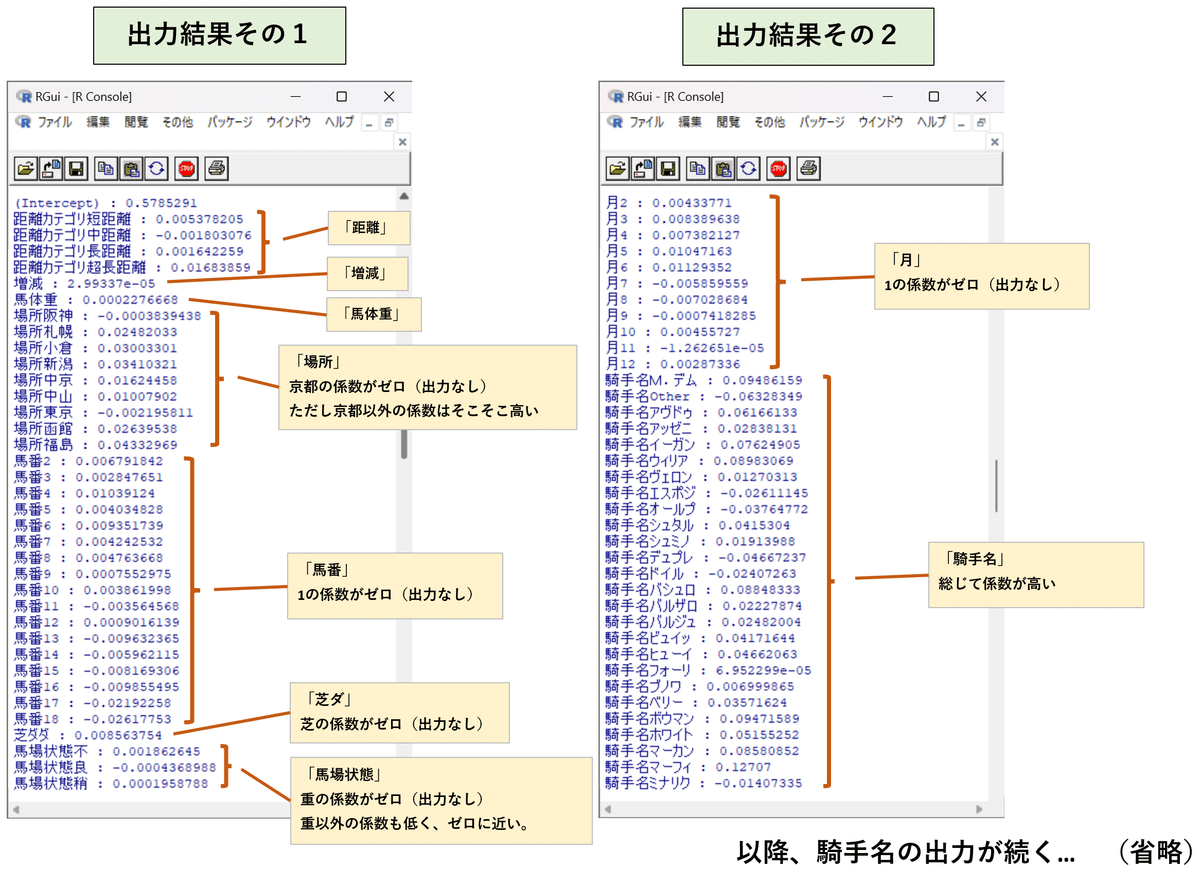
Lasso回帰（L1正則化）したモデルの各説明変数の影響度を出力

このような出力結果が得られました。
カテゴリカル変数のうち、いくつかのレベルで係数がゼロになり表示されていない事が確認できます。特に「馬場条件」では、重が係数ゼロに、良・不・稍の3つも係数がほぼゼロに近いため、目的変数に対する重要度は低いと考えられます。

　【9項目の特徴量に関する検証例②】
GBDTモデルを構築して、構築に使われた各説明変数の影響度を表示する例です。一旦全ての項目を含めたGBDTモデルを作り、GBDTモデル内の説明変数の影響度を出力することで、影響の度合いを数値として確認できます。

# 学習データの前処理
（省略）
#-----

# カテゴリカル変数を変換
（省略）
#-----

# モデル構築
（詳細後述）
#-----

# 説明変数の重要度を表示
Importance_Matrix <- xgb.importance(feature_names = colnames(MatrixData), model = xgb_model_1)
Categories <- list(
  距離カテゴリ = grep("^距離カテゴリ", colnames(MatrixData), value = TRUE),
  芝ダ = grep("^芝ダ", colnames(MatrixData), value = TRUE),
  馬場状態 = grep("^馬場状態", colnames(MatrixData), value = TRUE),
  場所 = grep("^場所", colnames(MatrixData), value = TRUE),
  月 = grep("^月", colnames(MatrixData), value = TRUE),
  馬番 = grep("^馬番", colnames(MatrixData), value = TRUE),
  馬体重 = grep("^馬体重", colnames(MatrixData), value = TRUE),
  増減 = grep("^増減", colnames(MatrixData), value = TRUE),
  騎手名 = grep("^騎手名", colnames(MatrixData), value = TRUE)
)
Category_Importance <- sapply(Categories, function(cols) {
  sum(Importance_Matrix$Gain[Importance_Matrix$Feature %in% cols])
})
print(Category_Importance)

出力結果は…

9項目の影響力を数値化

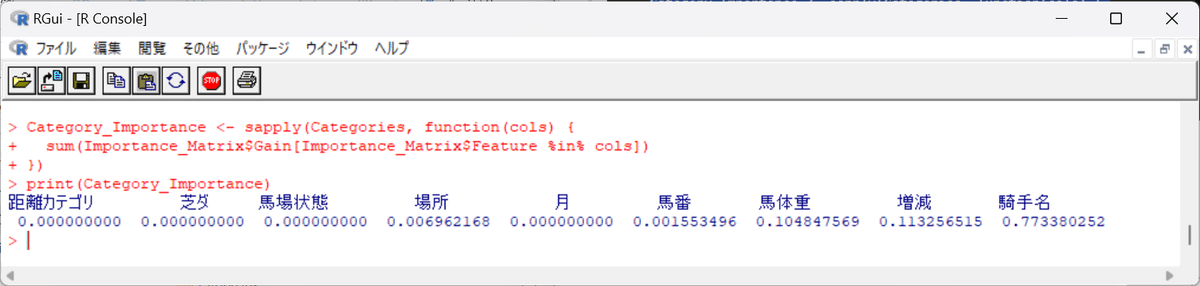
青字が出力結果です。各値を見ると、「騎手名」が0.7733…と最も高いことから、騎手の違いがその馬の強さ（着順に関する強さ）に大きく影響していることが読み取れます。反対に、「距離」「芝ダ」「馬場状態」「月」はゼロであり影響力がほぼありません。→要は、そもそも強い馬はこれら条件（馬場状態・芝ダなど）の如何に関わらず強いということ。

少し話が逸れましたが、このような分析例①や分析例②の結果も参考にしつつ、有効な特徴量の見極めを行ったり、汎化性UPに繋がる簡潔さ（説明しやすさ）のバランスを考えて最終的に判断を下します。
色々試した結果、ここでは次の6項目を説明変数に採用します。
「距離」「増減」「馬体重」「場所」「馬番」「騎手名」の6項目


GBDTを使った予測モデルの構築

「タスク」「目的変数」「説明変数」が全て決まりました。ここからは目的変数である着順指数を予測するためのGBDTモデルを作っていきます。

前項の通り、学習データ内のカテゴリカル変数は各レベルを明示してfactor型に変換します。（この後テストデータを使って予測を行う際にデータ項目の不一致が起こらないようにするため、各レベルを明示する必要あり）
また、学習データをDMatrix型というデータ型へ変換します。今回実装するXGBoostにおいてメモリ消費や計算コストを効率化できるデータ型です。

モデルの基本形

# 目的変数：「着順指数」
# 説明変数：「距離カテゴリ」「増減」「馬体重」「場所」「馬番」「騎手名」
Labels_1 <- JRAdata$着順指数
MatrixData_1 <- model.matrix(~ 距離カテゴリ * 増減 * 馬体重 + 場所 + 馬番 + 騎手名 - 1, JRAdata)

使用する説明変数６つのうち、「距離」「増減」「馬体重」の3項目を相互作用ありとして明示的に指示します。
※GBDTの性質上、説明変数間の相互作用項はある程度勝手に考慮されて学習が進むのですが、予め相互作用が期待されることが分かっている場合は明示的に指示します。

なおモデル訓練時は、学習データの一部を「検証用（＝バリデーション用）データ」として扱い、訓練度合いを自動制御することが一般的です。
学習データに対して過剰に適合したモデルを作ってしまうと汎化性能が落ちるため、検証用（＝つまりバリデーション用）データは直接訓練に使えません。もし直接訓練に使われると、答えを見ながら訓練している様なもので、正しいデータ特徴を捉えたモデルとは言い難くなります。
状況（サンプル数や計算負荷）に応じて、次の2つを使い分けます。
・Hold-Out法：学習データを予め学習用と検証用に切り分けておく方法。
　シンプルで計算も早いが、学習データの傾向が偏るリスクあり。
・Out-of-Fold法：学習データをk個のfoldに分割し、各foldを1度ずつ検証用に使う方法。
　「k-1個を学習用、1個を検証用」とした訓練を、全foldの組合せで実施。
　計算負荷が高いが、より正確な分析が可能。

今回は、Out-of-Fold法を採用します。
ここまでをRコードで書くと…

ここから先は

54,089字 / 6画像

¥ 10,000

この記事が気に入ったらサポートをしてみませんか？