パリティ追跡理論の基礎知識
こんにちは。
テトリスには地形の研究のためのパリティ追跡という理論 (Ogonek:Macronさん提唱) があります。
パリティ追跡を使った話題がリアルタイムで進行している時にその話の内容を理解したいという方、または地形の理論について詳しく知りたいという方へ、この理論の知っておくべき骨格の部分をまとめたいと思ってこの記事を作ってみました。
記事の最後ではLST積みのような同じ列での連続TSDについて考えます。
パリティ追跡理論とは
パリティと聞くと難しそうなイメージを持つと思います。
これは実際イメージ通りに難しいものなんですが、何事も鮮明に理解することで単純に感じられるようになります。
多くの人に雰囲気だけでも理解して帰ってもらいたくて、そのために分かりやすい言葉を使っていくのでよろしくお願いします!
パリティ追跡の目的は
「積みの中であるパリティの変化を追跡することで、今の地形の状態を把握し、どう積めばいいのか考える」
というところにあります。
パリティの変化について考える理論というわけですね。
パリティ追跡理論で使うパリティでは市松パリティの考え方を用いていて、これを理解するためには市松パリティについて十分に知っている必要があります。
市松パリティをそもそも知らなかったという方はぜひ調べてみてください。
この記事が分かりやすくておすすめです。
地形に名前をつける
地形のパリティを計算して、そのパリティの状態に名前をつけるという作業をします。
まずはこんな地形で考えてみましょう。

盤面を穴で分割
①この地形を穴の列で分割し、分割した両側で市松パリティをそれぞれ調べます。
また、後から都合を良くするために、調べる高さをTSDより上からの範囲とします。

パリティを計算
②青と黄で塗られたブロックの数を数えます。
左側では青が2ブロック、黄が2ブロック
右側では青が4ブロック、黄が4ブロック

③青-黄 を計算し、その値のmod4 (4で割ったあまり) を取ります。
左側では 2 - 2 = 0、0 ≡ 0 (mod 4)
右側でも 4 - 4 ≡ 0 (mod 4)
パリティの状態を文字で表す
④計算した値を偶数列側→奇数列側の順番になるように並べ替えます。
偶数列側 (ここでは4列の右) の値は0
奇数列側 (ここでは5列の左) の値は0
⑤計算した値を文字に置き換えます。
0 : α
1 : β
2 : γ
3 : δ
として、偶数列側→奇数列側の順に並べます。
0, 0だとααですね。
この地形の状態にααという名前をつけるわけです。

偶数列側で4パターン・奇数列側で4パターンと、計16種類に地形を分けることができました。
αα, αβ, αγ, αδ,
βα, ββ, βγ, βδ,
γα, γβ, γγ, γδ,
δα, δβ, δγ, δδ
TSDによるパリティの変化
次はパリティがどう変化していくのかを見ていきます。
パリティが変化する要因
このパリティの大元は市松パリティです。
市松パリティの定理として
「Tミノの設置やライン消しによってパリティが変化する」
というものがあるんですが、この定理をパリティ追跡理論にもそのまま使わせてもらいます。
・ライン消し
・Tミノの設置
後ほど詳しく書きますが、この記事ではTSD以外のライン消しやTSD以外のTミノ設置をしない動きについて考えます。
するとパリティが変化する条件はこのように置き換えられますね。
・TSD
パリティの変化を追うために、TSDの前後について詳しく調べていきます。
高さを偶数段上げる例
さて、TSDによってパリティにどんな変化が生まれるのでしょうか。
実際に数えてみましょう。
→青-黄のmod4



TSDの高さを2段上げました。
TSDによってαα→βδという変化が起きています。
詳しく言うと偶数列側でαはβに、奇数列側ではαはδに変化しました。
証明は省きますが、2段の高さ上げでは偶数列側で+1、奇数列側で-1という変化が起こるようです。
0 : α ↓ +1でαがβに
1 : β
2 : γ
3 : δ
0 : α ↑ -1でαがδに
偶数列側
α→β
β→γ
γ→δ
δ→α
奇数列側
α→δ
β→α
γ→β
δ→γ
そしてこの変化を使って16種類の地形を見てみると、なんと4本のループをつくることができました。
αα→βδ→γγ→δβ →αα
αβ→βα→γδ→δγ →αβ
αγ→ββ→γα→δδ →αγ
αδ→βγ→γβ→δα →αδ
高さを奇数段上げる例
もう一つ例を見てみましょう。
先ほどの例と比べて上げる高さが違う例です。



TSDによってαδ→ββという変化が起きました。
証明は省きますが、2という偶数段の高さ上げでは偶数列側で+1、奇数列側で-1という変化が起こるようです
偶数列側 α→β
奇数列側 δ→γ
αδ→βγ
偶数段の高さ上げの考え方だとαδはβγになっているはずで、そうでなくββになったということは、奇数段と偶数段では違う挙動をするようです。
ところで、今までTSDより上の範囲で市松状に塗り分けていましたよね。
実は範囲の最下段の右端と左端を青色にして、それを基準に市松状に広げていたんです。
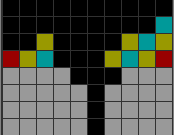
ここで例の2枚目と3枚目を見比べてみてほしいのですが、
TSDの高さを3段上げたことによって、なんと青と黄の塗り分けが反転しています!
また証明は省きますが、3という奇数段の高さ上げでは偶数列側で-1、奇数列側では変化しない、その後さらに塗り分けが反転するようです。
・偶数列側では-1という変化
0 : α
1 : β
2 : γ
3 : δ
0 : α ↑ -1でαがδに
・その後塗り分けが反転するとこんな変化
0 → -0 ≡ 0 : α
1 → -1 ≡ 3 : δ
2 → -2 ≡ 2 : γ
3 → -3 ≡ 1 : β (mod 4)
通して見るとこのように変化することが分かります。
偶数列側
α→β
β→α
γ→δ
δ→γ
奇数列側
α→α
δ→β
γ→γ
β→δ
少し複雑になりましたが、この例についても変化をまとめてみると、8本のループをつくることができました。
αα→βα →αα
αβ→βδ →αβ
αγ→βγ →αγ
αδ→ββ →αδ
γα→δα →γα
γβ→δδ →γβ
γγ→δγ →γγ
γδ→δβ →γδ
パリティを追跡する
2つのループをまとめる
さて、2種類の例を見ていきました。
例によって偶数段の高さ上げでは4本のループに、奇数段の高さ上げで8本のループに分けることができましたよね。
・偶数段 (周期4が4グループ)
αα→βδ→γγ→δβ→αα
αβ→βα→γδ→δγ→αβ
αγ→ββ→γα→δδ→αγ
αδ→βγ→γβ→δα→αδ
・奇数段 (周期2が8グループ)
αα→βα→αα
αβ→βδ→αβ
αγ→βγ→αγ
αδ→ββ→αδ
γα→δα→γα
γβ→δδ→γβ
γγ→δγ→γγ
γδ→δβ→γδ
奇数段の高さ上げと偶数段の高さ上げ、この2つは両方TSDという変換です。
できればこの2種類のループもまとめた形で表現してみたいですね。
両方のループを表現できる形を目指して、うまく組み合わせてみましょう。
ααという地形からは偶数段上げでβδへ、奇数段上げでβαへ変化する
αβという地形からは偶数段上げでβαへ、奇数段上げでβδへ変化する
αγという地形からは…
.
.
.
地形の変化
実際に組み合わせてみました。
なんと2つのグループに分かれたこんな図ができます。


赤矢印は偶数段の高さ上げ、
青矢印は奇数段の高さ上げによる変化を表しています。
非常に面白い形ですね。
矢印はTSDによるパリティ変化と言いました
図では2つのグループに分かれているんですが、これはTSDではグループを相互に移動できないということを表しています。
つまりどちらかのグループ内をずっと回り続けるという動きになるわけですね。
TSD継続のループ
そしてついにこの記事の最終目的であるTSDの継続に触れることができます!
TSD継続につける制約
・全巡でTSDをする (Tを積まない)
・TSD以外のライン消しをしない
・列をずらしたTSDを作らない (ドネイトなどをしない)
TSDを継続するという動きを考えた時、継続するということは良い地形をずっと保ちたいわけです。

地形についている色を見てみてください。
この色は地形の乱れを表しています。
水色 : 良い地形、ぜひ通りたい
黄色 : 片側が乱れた地形、短時間なら通ってよい
赤色 : 両側が乱れた地形、通りたくない
1つ目のグループは水色の地形が多いため、できることなら1枚目のグループ内に入っておいたほうがよさそうです。
安定したループ
地形の色と照らし合わせて図を見てみましょう。
TSD継続をしやすいループは何通りかあることが分かります。
グループ1 : 良い地形を通れる時間が長い
①αα→βδ→αβ→βα→αα
②αα→βα→αα
③αβ→βδ→αβ

グループ2 : 乱れた地形を通ることが多くなる
④αδ→ββ→γα→δα→αδ
⑤αδ→ββ→αδ
⑥δα→γα→δα

そしてこれらのループはテトリスで実際に使われている積み方にも当てはめることができます。
例えば特に有名な積み方だとこんなものがあります。
イメージがつくでしょうか。
②③⑤⑥ : 屋根の高さがずっと偶数段
①④ : 屋根の高さが奇数段と偶数段を交互に繰り返す
①④の例 : LST積み
②③⑤⑥の例 : ST積み
①②③や④⑤⑥を組み合わせた例 : 63積み
終わり
この記事では「こんな理論がある ! 」ということをとにかく理解してもらいたくて、一部背景や厳密なことを無視しているところがありました。
理論派の方、ぜひそこは優しい目で見てもらえると嬉しいです。
最後まで読んでみたけどよく分からなかった、結局どういう理論なのか分からない、という方は下に参考動画を置いているので見てみるといいでしょう。
もしかしたら理解の助けになるかもしれません。
では!
参考動画 : 地形からパリティ追跡を図示
記事用動画(修正版)
— 一般的暇人 (@ABABC_tec) January 28, 2025
パリティ追跡 pic.twitter.com/xi3veTrBmj
