英語力が高くなる要因を都道府県の各データから分析(中学校)

【経緯に関して】
私自身、教育業界の中の中学校や教育委員会へのセールスマーケティングに携わっていて、自分や周りの人たちの感覚で物事を決めるのではなく、たくさんのデータを基にした、明確で詳細な分析をしたいと考えていた。
英語教育は年々重要視されていて、各自治体は英語力向上のために、様々な取り組みを行っている。
その取り組みの中で、現状一番効果のある取り組みは何か?その結果から、今後どのような取り組みを行うことが好ましいと考えるか?など、これから今以上にグローバルな社会を生きていかなくてはならないが学生たちのために、より効果的な英語力向上施策が広まればと考えている。
元々データサイエンスに興味があって勉強をしていたが、勉強の成果の実践として、今回は表題のテーマでデータ分析を行った。
【事前の検討】
今回の目的は、英語力が高い生徒が多い地域の取り組みなどの特徴から、英語力を高める要因を考察することにある。
文科省が公表している「外国語教育政策」のデータの内、「英語教育実施状況調査」の「都道府県別一覧表」の表データを基に分析を行った。
平成30年度以前に関しては分析した結果のみ公表されていたり、調査項目が統一されていなかったりしため、今回は分析に含めなかった。令和元年以降は統一した項目で調査されたデータを公表していたため、こちらを使用した。
しかしながら、令和元年以降のデータを合わせるとデータ数が144件と少ない。少し過学習気味にしないと決定係数は上がらないと判断した。
そのため、決定係数の目標値を高めの0.8以上に設定した。
【特徴量】※ここは読み飛ばしても構いません。
文科省のデータは非常に細かい項目に分かれていたため、今回はなるべくシンプルに特徴量をまとめた。
Proficiency Test:英語能力に関する外部試験を受験したことがある生徒数
CEFR A1 students:CEFR A1レベル相当以上の英語力を取得または有すると思われる生徒数
language act students 50%:授業中、50%以上の時間、生徒が言語活動を行っている学校の割合
SW test:スピーキングテストとライティングテストを両方実施している学校の割合
CEFR B2 teachers:CEFR B2レベル以上を取得している英語担当教師数
language act teachers 50%:授業内で英語担当教師が50%以上の時間英語で発話している学校の割合
relation with ES_1:小学校と連携している(連携する予定)学校の割合
relation with ES_2:情報交換(互いの取組・実践を情報として交換する)を実施している学校の割合
relation with ES_3:交流(情報交換した内容について研究協議する。互いの学校で授業を行う)を実施している学校の割合
relation with ES_4:小中連携したカリキュラムや学習到達目標などの設定を実施している学校の割合
ICT_1:「生徒がパソコン等を用いて発表や話すことにおけるやり取りをする活動」を実施した学校の割合
ICT_2:「生徒による、発話や発音などの録音・録画」を実施した学校の割合
ICT_3:「生徒がキーボード入力等で書く活動」を実施した学校の割合
ICT_4:「生徒が電子メールやSNSを用いたやり取りをする活動」を実施した学校の割合
ICT_5:「生徒が遠隔地の生徒等と英語で話をして交流する活動」を実施した割合
ICT_6:「遠隔地の教師やALT等とティーム・ティーチングを行う授業」を実施した学校の割合
ICT_7:「生徒が遠隔地の英語に堪能な人と個別に会話を行う活動」を実施した学校の割合
※relation with ESとICTはいずれも「英語の授業において」
【CEFRについて】
因みに、ターゲットとする「CEFR A1 students」にあるCEFRというのは、「英語をはじめとした外国語の習熟度や運用能力を同一の基準で評価する国際標準」のことである。
要するに、「その言語を使って何ができるのか?」をレベルで示している。
特徴量にある「CEFR A1」は英検3級、「CEFR B2」は英検準1級くらいのレベルに値する。
【今回の検証の大まかな流れ】
目的変数と説明変数に分ける
Lasso回帰で不要な特徴量を割り出す。
累乗列・交互作用特徴量を列に追加。(決定係数が低ければ。)
Ridge回帰と重回帰でも測定。
その他のハイパーパラメータを調整
特徴量の重要度を可視化
はじめに高校データで分析
始めに令和1年度~4年度の高校のデータで検証しようと、上記の一通りの流れを繰り返し試した。しかし、Lasso回帰による各特徴量の係数はほぼ0と表示され、最も高くても約0.12という、どの特徴量も影響がないという結果になってしまった。また、いずれのモデルも決定係数が0.5を下回る結果となった。
利用できるデータ数の少なさや、高校のアンケートの質の疑念もあり、高校データの分析は打ち切って、別のところを見ることにした。
次は中学校のデータで、高校と同じ手順で検証してみたのだが、高校に比べてハッキリと高い決定係数を得られたため、中学校で進めることにした。
高校より良い結果を得られた理由として、高校よりも中学校の方がデータ数が多いこと、高校生より中学生の方が真面目に回答してくれていること、などと私自身は推測している。
中学校データで分析
中学校データと高校データの違いは、調査項目とデータ数であった。データ数に関して、高校は都道府県ごとであったのに対し、中学校は都道府県に加えて全国の主要な県庁所在地も含まれていた。
始めは中学校も特徴量が統一されている令和1~4年のデータを利用していた。特徴量の中の「ICT_1」~「ICT_7」に関しては令和以降のデータにしかなかったが、平成30年度に関しては、「ICT_1」~「ICT_7」以外の特徴量は令和以降と同様のものであった。
ICTの重要度がそれほど高くなかったことや、データ数を少しでも増やしたかったため、平成30年度のデータも加えた。また、ICT関連の特徴量は削除した。(ICTが重要にならなかった理由の考察は、最後の「考察」に記載。)
【コーディング】
中学校のデータで分析した際に使用したコードを紹介する。全てを記載すると非常に長くなってしまうため、一部のみであることをご了承いただきたい。
0.前処理
import pandas as pd
%matplotlib inline
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Lasso
from sklearn.linear_model import Ridge
import numpy as np
from sklearn.neighbors import LocalOutlierFactor
df_h30 = pd.read_csv("平成30年度(中学校).csv")
df_r1 = pd.read_csv("令和1年度(中学校).csv")
df_r3 = pd.read_csv("令和3年度(中学校).csv")
df_r4 = pd.read_csv("令和4年度(中学校).csv")
df = pd.concat([df_h30, df_r1, df_r3, df_r4], axis=0)
df = df.reset_index(drop=True)上記のコーディングの後に完成した「df」という名称のデータフレームの頭と後ろの各5行が下記になる。いずれの数値も、文科省のサイトの時点では%で表記されていたものを小数点に変換したものである。

「Unnamed: 0」、「Unnamed: 1」、「ICT_1」~「ICT_7」は今回不要なので削除。
# 「ICT_1」~「ICT_7」や不要な特徴量は削除。
df2 = df.drop(df.iloc[:, 12:], axis=1)
df3 = df2.drop(df.iloc[:, :2], axis=1)1.目的変数と説明変数に分ける
上記コードで作成したdf3に欠損値は無かった。
df3を目的変数と説明変数に分ける。目的変数は、中学生の英語レベルを示す「CEFR A1 students」。
# df3を目的変数と説明変数に分ける。
x = df3.drop(["CEFR A1 students"], axis=1)
t = df3["CEFR A1 students"]2.Lasso回帰で不要な特徴量を割り出す。
実際に重要な特徴量は少しと思われるため、影響の少ない係数を0にできる特徴を持つLasso回帰をモデルに使用する。
はじめに、Lassoの重要なハイパーパラメータであるalphaに入る最適な正則化項をfor文により割り出す。(下記コードでは10,000,000分の1から10,000,000分の1,000で実行していますが、実際は様々な数字で試している。)
test_sizeは、データ数が少ない中で学習させるため、少なめの0.1にとりあえず設定した。
また、Scikit-learnの”LocalOutlierFactor”により、n_neighbors=20として訓練データから外れ値を削除している。(n_neighborsはいくつかの数値で試し、20に落ち着いた。)
# Lasso回帰①で使う正則化項を割り出す。
maxScore = 0
maxIndex = 0
x_train, x_test, y_train, y_test = train_test_split(x, t, test_size=0.1, random_state=0)
clf = LocalOutlierFactor(n_neighbors=20)
predictions = clf.fit_predict(x_train)
outliers_index = x_train.index[predictions == -1]
x_train = x_train.drop(outliers_index, axis=0)
y_train = y_train.drop(outliers_index, axis=0)
for i in range(1, 1001):
num = i / 10000000
lasso = Lasso(random_state=0, alpha= num)
lasso.fit(x_train, y_train)
result= lasso.score(x_test, y_test)
if result > maxScore:
maxScore = result
maxIndex = num
print(maxIndex, maxScore)alphaに入れる最適な数字は1e-07で、
その際の決定係数は0.47628983539671743という結果であった。
# ラッソ回帰(1)
lasso = Lasso(alpha = 1e-07)
x_train, x_test, y_train, y_test = train_test_split(x, t, test_size=0.1, random_state=0)
clf = LocalOutlierFactor(n_neighbors=20)
predictions = clf.fit_predict(x_train)
outliers_index = x_train.index[predictions == -1]
x_train = x_train.drop(outliers_index, axis=0)
y_train = y_train.drop(outliers_index, axis=0)
lasso.fit(x_train, y_train)
print(lasso.score(x_train, y_train))
print(lasso.score(x_test, y_test))訓練データ:0.3731324018929134
テストデータ:0.47628983539671743
という結果であった。
係数の絶対値も確認する。
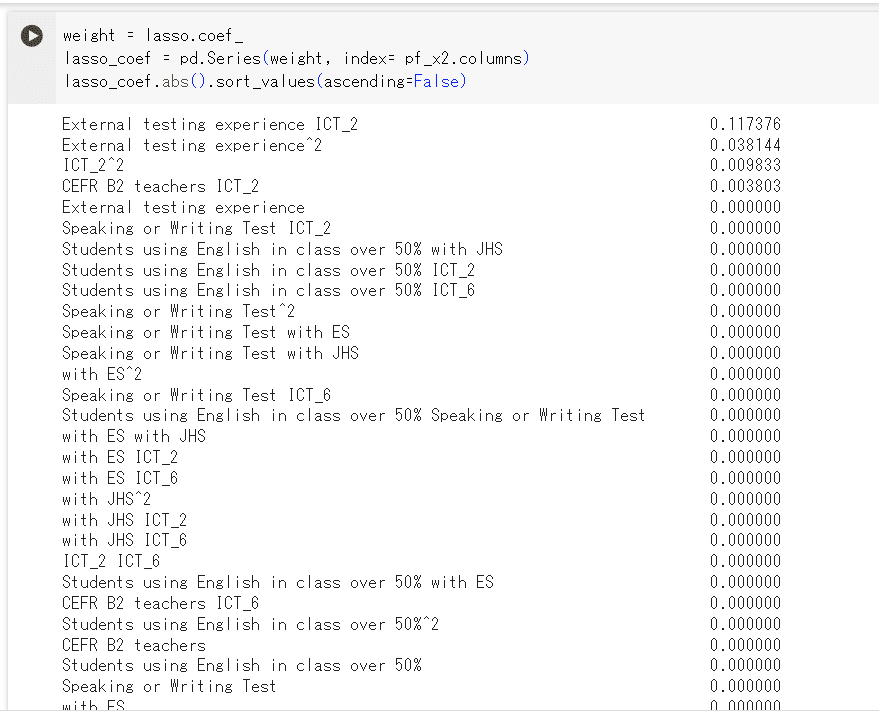
# Lasso回帰(1)の係数を絶対値で降順に並び替える。
weight = lasso.coef_
lasso_coef = pd.Series(weight, index= x_train.columns)
display(lasso_coef.abs().sort_values(ascending=False))
3.累乗列・交互作用特徴量を列に追加。
Lassoによる決定係数が0.5を下回り、且つ係数の方も重みをハッキリ判断できるほどでは無い。この結果では他のモデルでも期待する結果は得られないだろうと考え、この段階で累乗列と交互作用特徴量を追加してみる。
# 累乗列と交互作用特徴量を一括追加する
from sklearn.preprocessing import PolynomialFeatures
pf = PolynomialFeatures(degree= 2, include_bias= False)
pf_x = pf.fit_transform(x)
pf_x = pd.DataFrame(pf_x, columns= pf.get_feature_names_out())その上で、もう一度Lasso回帰をする。
# Lasso回帰(2)で使う正則化項を割り出す。
maxScore = 0
maxIndex = 0
x_train, x_test, y_train, y_test = train_test_split(pf_x, t, test_size=0.1, random_state=0)
clf = LocalOutlierFactor(n_neighbors=20)
predictions = clf.fit_predict(x_train)
outliers_index = x_train.index[predictions == -1]
x_train = x_train.drop(outliers_index, axis=0)
y_train = y_train.drop(outliers_index, axis=0)
for i in range(1, 1001):
num = i / 1000000
lasso = Lasso(random_state=0, alpha= num)
lasso.fit(x_train, y_train)
result= lasso.score(x_test, y_test)
if result > maxScore:
maxScore = result
maxIndex = num
print(maxIndex, maxScore)alphaに入れる最適な数字は1.5e-05で、
その際の決定係数は0.7764073597183494という結果になった。
# Lasso回帰(2)
lasso = Lasso(alpha = 1.5e-05)
x_train, x_test, y_train, y_test = train_test_split(pf_x, t, test_size=0.1, random_state=0)
clf = LocalOutlierFactor(n_neighbors=20)
predictions = clf.fit_predict(x_train)
outliers_index = x_train.index[predictions == -1]
x_train = x_train.drop(outliers_index, axis=0)
y_train = y_train.drop(outliers_index, axis=0)
lasso.fit(x_train, y_train)
print(lasso.score(x_train, y_train))
print(lasso.score(x_test, y_test))訓練データ:0.5602324760195222
テストデータ:0.7764073597183494
となった。
訓練データとの差が0.2もあることが気になるが、決定係数は0.3も向上した。
係数の絶対値も確認したところ、ハッキリと重みの度合いを割り出すことができた。

・

特徴量が54ある中で約半数が0.1以下であったため、まとめて削除。
# Lasso回帰(2)で係数の値が0.1以下の特徴量をすべて削除
selected_features = lasso_coef[lasso_coef.abs() > 0.1].index
pf_x2 = pf_x[selected_features]その上で、これまでと同様のコードでLasso回帰をしてみたところ、下記の結果となり、あまり変化は見られなかった。
訓練データ:0.552848176644446
テストデータ:0.7714042914324568
削除する係数の値の範囲を変更して試したが、上記コード記載の0.1以下の時が最も高かった。
4.重回帰とRidge回帰でも同様に決定係数を測定。
ここで、重回帰とRidge回帰でも試してみる。
まずは重回帰を実行。
# 重回帰分析(1)
x_train, x_test, y_train, y_test = train_test_split(pf_x2, t, test_size=0.1, random_state=0)
clf = LocalOutlierFactor(n_neighbors=20)
predictions = clf.fit_predict(x_train)
outliers_index = x_train.index[predictions == -1]
x_train = x_train.drop(outliers_index, axis=0)
y_train = y_train.drop(outliers_index, axis=0)
model =LinearRegression()
model.fit(x_train, y_train)
print(model.score(x_train, y_train))
print(model.score(x_test, y_test))訓練データ:0.5615162434396436
テストデータ:0.7596325566528671
となり、Lassoとあまり変わらず。
次にRidge回帰を実行してみる。
# リッジ回帰(1)で使う正則化項を割り出す。
x_train, x_test, y_train, y_test = train_test_split(pf_x2, t, test_size=0.1, random_state=0)
clf = LocalOutlierFactor(n_neighbors=20)
predictions = clf.fit_predict(x_train)
outliers_index = x_train.index[predictions == -1]
x_train = x_train.drop(outliers_index, axis=0)
y_train = y_train.drop(outliers_index, axis=0)
maxScore = 0
maxIndex = 0
for i in range(1, 1001):
num = i / 100000
ridge = Ridge(random_state=0, alpha= num)
ridge.fit(x_train, y_train)
result= ridge.score(x_test, y_test)
if result > maxScore:
maxScore = result
maxIndex = num
print(maxIndex, maxScore)alphaに入れる最適な数字は0.00297で、
その際の決定係数は0.7814446363041967という結果であった。
# リッジ回帰(1)
ridge = Ridge(alpha = 0.00297)
pf_x_train, pf_x_test, y_train, y_test = train_test_split(pf_x2, t, test_size=0.1, random_state=0)
x_train, x_test, y_train, y_test = train_test_split(pf_x2, t, test_size=0.1, random_state=0)
clf = LocalOutlierFactor(n_neighbors=20)
predictions = clf.fit_predict(x_train)
outliers_index = x_train.index[predictions == -1]
x_train = x_train.drop(outliers_index, axis=0)
y_train = y_train.drop(outliers_index, axis=0)
ridge.fit(x_train, y_train)
print(ridge.score(x_train, y_train))
print(ridge.score(x_test, y_test))訓練データ:0.555355232428772
テストデータ:0.7814446363041967
という結果になり、僅かに高くなったが目標には届いていない。
5.その他のハイパーパラメータを調整
alpha以外のハイパーパラメータの調整も試みた。
まずは影響が大きいであろうtest_sizeで、最も決定係数が高くなる数値を検索した。
はじめにLasso回帰から。
(下記コードでは10000分の1から10000分の1000までの範囲で実行しているが、実際はもっと複数の範囲で実行している。)
# ラッソ回帰(3)※test_sizeを変更
maxScore = 0
maxIndex = 0
for i in range(1, 1001):
tes = i / 10000
x_train, x_test, y_train, y_test = train_test_split(pf_x2, t, test_size= tes, random_state=0)
lasso = Lasso(random_state=0, alpha= 1e-05)
clf = LocalOutlierFactor(n_neighbors=20)
predictions = clf.fit_predict(x_train)
outliers_index = x_train.index[predictions == -1]
x_train = x_train.drop(outliers_index, axis=0)
y_train = y_train.drop(outliers_index, axis=0)
lasso.fit(x_train, y_train)
result= lasso.score(x_test, y_test)
if result > maxScore:
maxScore = result
maxIndex = tes
print(maxIndex, maxScore)test_sizeに入れる最適な数字は0.0784で、
その際の決定係数は0.8324296045067519という結果であった。
# Lasso回帰(3)※最適なtest_sizeで実行
lasso = Lasso(alpha = 1e-05)
x_train, x_test, y_train, y_test = train_test_split(pf_x2, t, test_size=0.0784, random_state=0)
clf = LocalOutlierFactor(n_neighbors=20)
predictions = clf.fit_predict(x_train)
outliers_index = x_train.index[predictions == -1]
x_train = x_train.drop(outliers_index, axis=0)
y_train = y_train.drop(outliers_index, axis=0)
lasso.fit(x_train, y_train)
print(lasso.score(x_train, y_train))
print(lasso.score(x_test, y_test))訓練データ:0.5406822894384359
テストデータ:0.8324296045067519
という結果になった。
目標の決定係数に到達したが、訓練データとの差が気になる。
重回帰とRidgeでも、同様に決定係数が最大になるtest_sizeを割り出した。
コードは繰り返しになるので、割愛する。
<重回帰>
test_sizeに入れる最適な数字は0.0038で、その際の決定係数は0.838205718251517という結果となり、
訓練データ:0.5376616564982628
テストデータ:0.838205718251517
となった。
<Ridge回帰>
test_sizeに入れる最適な数字は0.0784で、その際の決定係数は0.82805604579159という結果となり、
訓練データ:0.5340052222057576
テストデータ:0.82805604579159
となった。
最も高いのは重回帰であるが、test_sizeが0.0038とあまりに小さすぎる。
LassoとRidgeも0.8を超える結果になったものの、訓練データとの差が大きく、テストデータがたまたま正確なものだった、と言わざるを得ない。
因みに、グリッドサーチとランダムサーチを3つすべてのモデルで試そうとしたが、私が使用していたGoogleColaboratoryとVisual Studio Code共に、MemoryErrorが起きてしまい断念した。下記のコードで実行予定だった。(全て記載すると冗長になるので、Lassoのグリッドサーチのみ表記する。)
# Lasso回帰をグリッドサーチ
from sklearn.model_selection import GridSearchCV
lasso_set_grid = {Lasso(): {"alpha":[i / 100 for i in range(1, 1001)],
"fit_intercept":[True, False],
"precompute":[True, False],
"copy_X":[True, False],
"max_iter":[i for i in range(1, 1001)],
"tol":[i / 10000 for i in range(1, 1001)],
"warm_start":[True, False],
"positive":[True, False],
"random_state":[0],
"selection":["cyclic","random"]}}
max_score = 0
best_param = None
x_train, x_test, y_train, y_test = train_test_split(pf_x2, t, test_size=0.1, random_state=0)
# グリッドサーチでハイパーパラメーターを探索
for model, param in lasso_set_grid.items():
clf = GridSearchCV(model, param)
clf.fit(x_train, y_train)
score = lasso.score(x_test, y_test)
if max_score < score:
max_score = score
best_param = clf.best_params_
print("ハイパーパラメーター:{}".format(best_param))
print("ベストスコア:",max_score)一応、"max_iter"や"tol"は単体でそれぞれパラメータ調整を試してみたが、いずれも結果はほとんど変わらなかった。
6.特徴量の重要度を可視化
訓練データとテストデータの差は開いたままではあるが、データ数を少なくとも1,000以上に増やさないと難しそうだ。データ元の文科省が公表しているデータはこれ以上ないため、検証はここまでとする。
最も決定係数の高いモデルは重回帰であるが、test_sizeがあまりに小さい。LassoとRidgeはtest_sizeが同じで、Lassoの方が若干高いため、Lassoを完成モデルとする。
Laasoによる係数(重み)の絶対値を確認する。
#Lasso回帰による係数(重み)を調べる
weight = lasso.coef_
lasso_coef = pd.Series(weight, index= x_train.columns)
display(lasso_coef.abs().sort_values(ascending=False))
特徴量の数が多いため、係数の絶対値が0.5以上の係数に絞った上で、+-の値に戻した係数を棒グラフで可視化する。
import matplotlib.pyplot as plt
# 値が0.5以上のカラムを抽出
selected_columns = lasso_coef[lasso_coef.abs() >= 0.5]
# 棒グラフで表示
plt.figure(figsize=(10, 6))
selected_columns.sort_values(ascending=False).plot(kind='bar')
plt.title('Characteristics of regions with high English proficiency')
plt.xlabel('Column')
plt.ylabel('Coefficient')
plt.xticks(rotation=90)
plt.show()

【英語力向上に必要な要素を考察】
<特徴量の係数から見る重要な特徴>
英語力の高い生徒の多さに、最もプラスの方向に影響を与えているのが「”language act students 50%”:授業中、50%以上の時間、生徒が言語活動を行っている学校の割合」という結果であった。
日本の英語教育の課題として近年挙げられているのが、日本はリーディングとライティングに注力してきた故に、知識はあるけど話せないという問題だ。知識をアウトプットする活動を授業の中で設けることで、生徒の英語力に寄与することを数値で表していると言えよう。
また、最もマイナスの方向に影響を与えているのが、上記の”language act students 50%”と「”relation with ES_1”:小学校と連携している(連携する予定)学校の割合」の掛け合わせであった。
言語活動を多く行っている中学生からすると、自身よりまだ英語が未熟な小学生との会話はプラスにはならない、ということになるのだろうか。それでもマイナスとまではならないと思うが、連携の仕方に問題があるのだろうか。
”relation with ES_1”単体では5番目に高い係数になっているので、もしかしたら「中学生の英語力(=言語活動の量)に合わせた連携の仕方」が重要なのかもしれない。
他にも、「”CEFR B2 teachers”:CEFR B2レベル以上を取得している英語担当教師数」は単体だとマイナスの影響を与えるが、取り組みの組み合わせによってはプラスの影響を与える、という点も気になるところだ。
「”Proficiency Test”:英語能力に関する外部試験を受験したことがある生徒数」との掛け合わせは2番目に係数が高い。
英検など目標を示されている場合は、英語力の高い教師の指導がプラスの影響を与え、特にそういった目標が無ければ、英語力の高い教師はマイナスの影響を与えるということになるか。
これが示すのは、生徒の英語へのモチベーションと、教師の英語レベルは影響を及ぼし合っている、ということではないだろうか。
<除外した特徴量「ICT_1」~「ICT_7」について>
ICTとはいわゆるデジタル教材の利用に関する項目のことだ。これが重要項目にならなかったのは、恐らくICTの普及が最近であったことや、授業の中でまだ使いこなされていないことなどが考えられる。これは、私自身が学校や教育委員会に営業をしていても実感しているところだ。
【今後について】
データ数が少なかったり、テストデータと訓練データの決定係数の差が大きすぎたりなど、あまり精度の高いモデルは作成できなかったと思う。
あわよくばこの結果を今の会社でマーケティングに活かしたいと考えていたが、それは難しそうだ。
もっと機械学習や統計学の知識を深められれば、今回の場合でももっと別の結果を得られたかもしれない。勉強はしつつも、実践的な取り組みも並行して続け、より高度な考察とマーケティング分析を行えるようにしたい。
